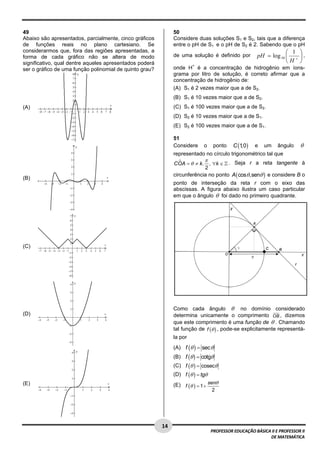
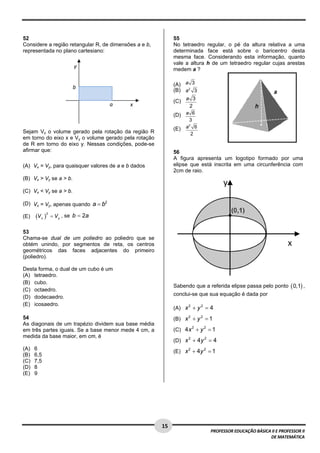
Este documento apresenta instruções para a realização de uma prova de promoção por merecimento do quadro de magistério para professores de educação básica e de matemática. As instruções incluem: 1) verificar o material recebido, 2) assinar o cartão de respostas, 3) marcar as respostas nas alternativas fornecidas, 4) entregar o caderno de questões e cartão de respostas após 4 horas e 30 minutos. O candidato será eliminado se utilizar dispositivos eletrônicos, sair da sala levando