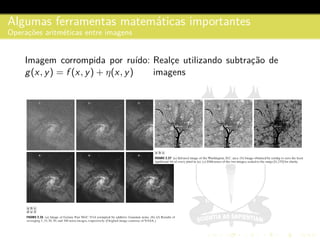
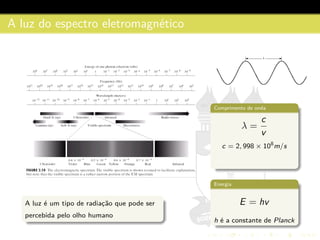
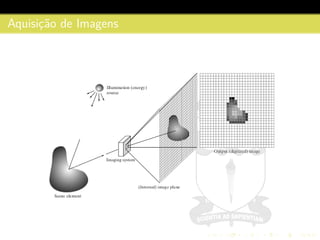
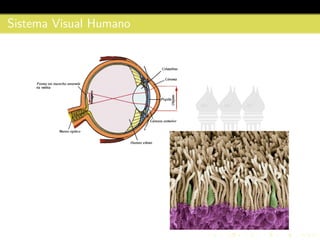
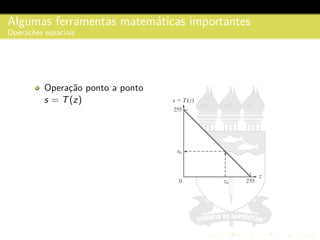
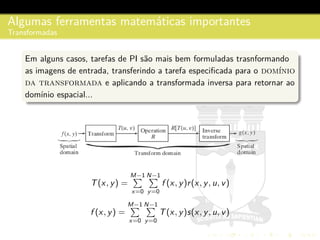
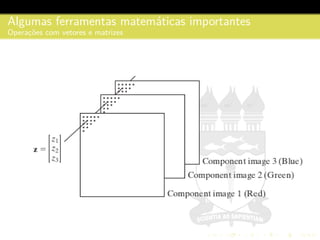
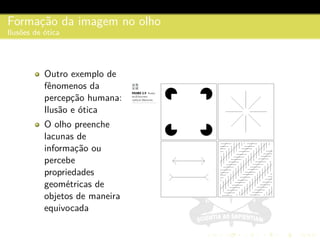
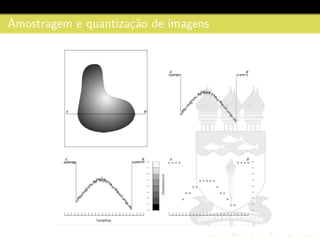
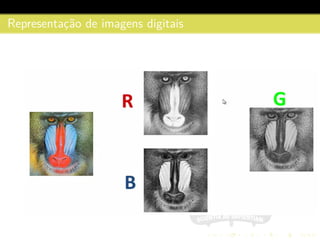
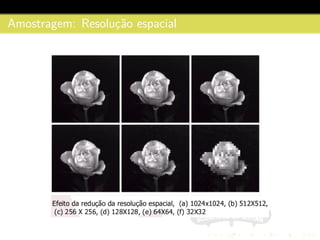
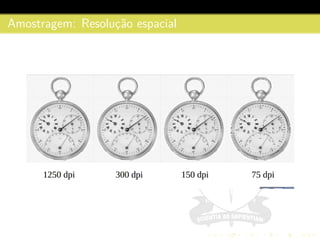
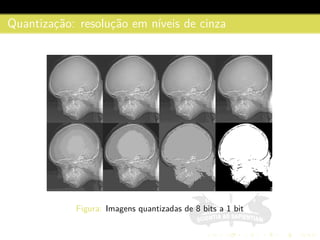
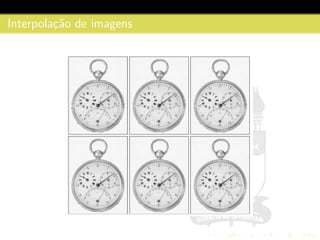
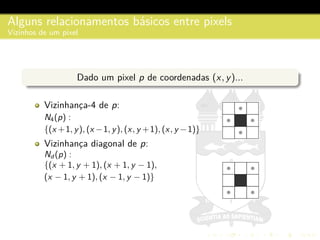
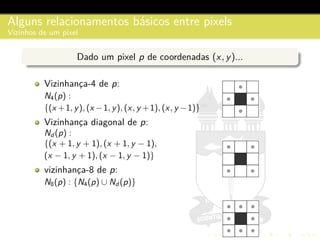
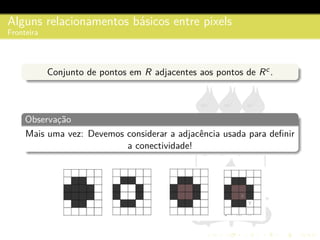
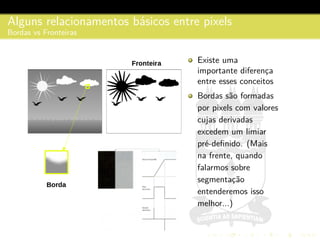
1) O documento discute fundamentos da imagem digital, incluindo a natureza da luz, formação de imagens no olho humano, aquisição e representação de imagens digitais. 2) É explicado como a luz interage com o Sistema Visual Humano através da retina, e como as células de cones e bastonetes percebem cores e luminosidade. 3) São descritos conceitos como amostragem, quantização, interpolação e relacionamentos entre pixels na representação digital de imagens.

1. Fundamentos da Imagem Digital
Fabiane Queiroz
fabiane.queiroz@arapiraca.ufal.br
Ciˆencia da Computac¸˜ao - UFAL - Campus Arapiraca

2. A luz do espectro eletromagn´etico
A luz ´e um tipo de radiac¸˜ao que pode ser
percebida pelo olho humano
Comprimento de onda
λ =
c
v
c = 2, 998 × 108
m/s
Energia
E = hv
h ´e a constante de Planck

3. A luz do espectro eletromagn´etico
Radiˆancia, luminˆancia e brilho
As cores percebidas por n´os em um
objeto s˜ao determinadas pela
natureza da luz refletida pelo
objeto
A radiˆancia ´e a quantidade total
de energia que ´e emitida pela fonte
de luz
A luminˆancia mede a quantidade
de energia que um observador
percebe de uma fonte de luz
O brilho ´e um descritor subjetivo
da percepc¸˜ao da luz que ´e
praticamente imposs´ıvel de
mensurar

4. Sistema Visual Humano
A retina ´e a ´area do olho que recebe a luz, transforma em
sinais nervosos e transmite para o c´erebro atrav´es dos nervos
´oticos
A retina do olho humano cont´em dois tipos de c´elulas que
detectam a luz e a transformam em impulsos nervosos: Cones
e Bastonetes
Vis˜ao fot´opica: Os cones s˜ao aproximadamente seis a sete
milh˜oes e s˜ao sens´ıveis a alto n´ıvel de iluminac¸˜ao e
respons´aveis pela percep¸c˜ao das cores (vermelho, verde e
azul)
Vis˜ao Escot´opica: Os bastonetes s˜ao aproximadamente 125
milh˜oes, s˜ao sens´ıveis a baixo n´ıvel de iluminac¸˜ao, distinguem
os tons de cinza e s˜ao respons´aveis pela vis˜ao perif´erica

5. Sistema Visual Humano

6. Sistema Visual Humano
Muitos animais vˆem
outras partes do
espectro
As abelhas s˜ao
sens´ıveis aos UV
Os c˜aes e gatos
s˜ao muito pouco
sens´ıveis `a cor

7. Formac¸˜ao da imagem no olho
15
100
=
x
17
x = 2, 55mm
Em uma cˆamera fotogr´afica comum, a lente tem uma distˆancia
focal fixa.
A focalizac¸˜ao ´e obtida variando-se a distˆancia entre a lente e o
plano-imagem (chip de captura ou filme) da imagem.
No olho humano, ocorre o contr´ario: A distˆancia entre a lente e o
plano-imagem ´e fixa, a distˆancia focal ´e obtiva variando o formato
do cristalino (o que equivale a uma lente flex´ıvel)
A distˆancia entre o centro focal do cristalino e a retina varia de
17mm a 14mm

8. Formac¸˜ao da imagem no olho
Adaptac¸˜ao ao brilho e discriminac¸˜ao
O sistema visual humano pode perceber, aproximadamente
1010 diferentes n´ıveis de intensidade luminosa.
Por´em, o sistema visual humano n˜ao opera simultaneamente
em cima dessa faixa e s´o podemos discriminar entre um
n´umero muito menor de n´ıveis de intensidade luminosa -
adapta¸c˜ao brilho
A intensidade da percepc¸˜ao de uma regi˜ao est´a relacionada
com a intensidade de luz de regi˜oes que o rodeiam.

9. Formac¸˜ao da imagem no olho
Ilus˜oes de ´otica
Outro exemplo de
fˆenomenos da
percepc¸˜ao humana:
Ilus˜ao e ´otica
O olho preenche
lacunas de
informac¸˜ao ou
percebe
propriedades
geom´etricas de
objetos de maneira
equivocada

10. Aquisic¸˜ao de Imagens

11. Aquisic¸˜ao de Imagens

12. Revisando rapidamente o que vimos na ultima aula...
A imagem como uma func¸˜ao (sinal) cont´ınua e amostragem e quantizac¸˜ao de imagens...
Uma imagem pode ser cont´ınua em relac¸˜ao as coordenadas x
e y e tamb´em em relac¸˜ao a amplitude
Dada uma imagem cont´ınua f queremos convertˆe-la para o
formato digital
A digitalizac¸˜ao dos valores de coordenadas ´e chamado
amostragem
A digitalizac¸˜ao dos valores de amplitude ´e chamado
quantiza¸c˜ao

13. Amostragem e quantizac¸˜ao de imagens

14. Amostragem e quantizac¸˜ao de imagens
Imagem cont´ınua projetada sobre o plano de uma matriz e imagem
ap´os amostragem e quantizac¸˜ao:
A qualidade da imagem digital ´e claramente determinada, em
grande parte, pelo n´umero de amostras utilizados na amostragem e
quantizac¸˜ao.

15. Representac¸˜ao de imagens digitais
Representac¸˜ao gr´afica, matriz de intensidades e matriz num´erica
O valor da imagem em quaisquer coordenadas (x, y) ´e f (x, y) para x e y inteiros.
A sec¸˜ao do plano que se expande pelas coordenadas de uma imagem ´e chamada de
dom´ınio espacial e x e y s˜ao coordenadas espaciais.

16. Representac¸˜ao de imagens digitais
=


f (0, 0) f (0, 1) · · · f (0, N − 1)
f (1, 0) f (1, 1) · · · f (1, N − 1)
.
.
.
.
.
.
.
.
.
.
.
.
f (M − 1, 0) f (M − 1, 1) · · · f (M − 1, N − 1)


A =



a0,0 a0,1 · · · a0,N−1
a1,0 a1,1 · · · a1,N−1
...
...
...
...
aM−1,0 aM−1,1 · · · aM−1,N−1



ai,j = f (x = i, y = j) = f (i, j)
... Podemos representar uma imagem at´e or um vetor linha v de
tamanho MX × 1, ou um vetor coluna vt de tamanho 1 × MN.

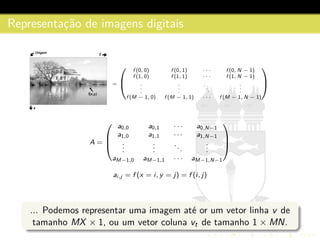
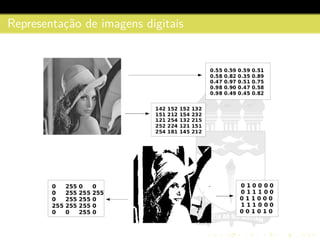
17. Representac¸˜ao de imagens digitais
O n´umero de n´ıveis de intensidade costumam ser igualmente
espac¸ados no intervalo [0, L − 1] e representados por uma potˆencia
inteira de 2: L = 2k, onde k ´e o n´umero de bits armazenado por
pixel.
O n´umero b de bits necess´arios para armazenar uma imagem
digitalizada ´e b = MxNxk
(Para M = N, b = N2k)

18. Representac¸˜ao de imagens digitais
Alguns conceitos importantes...
Faixa dinˆamica:Faixa dinˆamica:
Quantidade m´axima de contraste que um filme (ou um sensor
para cˆameras digitais) pode capturar.
Contraste:Contraste:
Diferenc¸a entre os n´ıveis superior e inferior presente em uma
image.
Quando um n´umero significativo de pixels em uma imagem possui uma alta
faixa dinˆamica, podemos esperar que a imagem tenha um alto contraste.

19. Representac¸˜ao de imagens digitais

20. Representac¸˜ao de imagens digitais

21. Amostragem: Resoluc¸˜ao espacial
A Resoluc¸˜ao espacial em
geral, ´e medida em pontos
por polegada ou DPI (dots
per inch)
n´umero de pixels =
resoluc¸˜ao x tamanho real.
Quando duas imagens com tamanhos reais
iguais s˜ao capturadas com resoluc¸˜oes
diferentes, naturalmente ter˜ao n´umero de
pixels diferentes e na tela aparecer˜ao com
tamanhos diferentes

22. Amostragem: Resoluc¸˜ao espacial

23. Amostragem: Resoluc¸˜ao espacial

24. Amostragem: Resoluc¸˜ao espacial

25. Amostragem: Resoluc¸˜ao espacial
Quando duas imagens de
tamanhos reais diferentes
s˜ao capturadas com
resoluc¸˜oes iguais de tal
forma que gerem imagens
digitais com o mesmo
n´umero de pixels, quando
visualizadas no monitor
aparecer˜ao com o mesmo
tamanho na tela.
Figura: Duas imagens com diferentes tamanhos
reais, mas com igual resoluc¸˜ao e tamanhos 256x256 na
tela

26. Quantizac¸˜ao: resoluc¸˜ao em n´ıveis de cinza
Figura: Imagens quantizadas de 8 bits a 1 bit

27. Interpolac¸˜ao de imagens
Interpolac¸˜ao ´e o processo que utiliza dados conhecidos para
estimar valores em pontos desconhecidos
Ferramenta utilizada extensivamente utilizada em tarefas
como redimensionamento (ampliac¸˜ao e reduc¸˜ao), rotac¸˜ao e
correc¸˜oes geom´etricas.
Redimensionar implica em reamostrar

28. Interpolac¸˜ao de imagens
Interpolac¸˜ao pelo vizinho mais pr´oximo
Considere uma imagem 500x500 e uma ampliac¸˜ao para
750x750;
Imagine um grid 750x750 com o mesmo espac¸amento de
pixels;
Reduza o grid para se sobrepor a imagem de 500x500;
Atribua a cada posic¸˜ao do grid 750x750 um valor de pixel
mais pr´oximo na imagem original;
Expanda o grid 750x750 para seu espac¸amento original

29. Interpolac¸˜ao de imagens
Interpolac¸˜ao pelo vizinho mais pr´oximo
Desvantagem: Efeito de
blocos
Vantagens:
Processamento r´apido
N˜ao cria novos valores
de NC (mant´em
estat´ısticas da imagem)

30. Interpolac¸˜ao de imagens
Interpolac¸˜ao bilinear
Utiliza os 4 vizinhos mais
pr´oximo para estimar a
itensidade de uma dada
posic¸˜ao
f (x, y) = ax+by +cxy +d
Resultados melhores com
um pequeno aumento de
custo computacional
N˜ao mantem as
estat´ısticas das imagens!

31. Interpolac¸˜ao de imagens

32. Interpolac¸˜ao de imagens
Interpolac¸˜ao bi´ubica
Utiliza os 16 vizinhos
mais pr´oximo para estimar
a itensidade de uma dada
posic¸˜ao
f (x, y) =
3
i=0
3
j=0
aijxi yj
´E melhor na preservac¸˜ao
de detalhes
Usada no Adobe
Photoshop, Corel
Photopaint, etc.

33. Interpolac¸˜ao de imagens

34. Alguns relacionamentos b´asicos entre pixels
Vizinhos de um pixel
Dado um pixel p de coordenadas (x, y)...
Vizinhanc¸a-4 de p:
N4(p) :
{(x +1, y), (x −1, y), (x, y +1), (x, y −1)}

35. Alguns relacionamentos b´asicos entre pixels
Vizinhos de um pixel
Dado um pixel p de coordenadas (x, y)...
Vizinhanc¸a-4 de p:
N4(p) :
{(x +1, y), (x −1, y), (x, y +1), (x, y −1)}
Vizinhanc¸a diagonal de p:
Nd (p) :
{(x + 1, y + 1), (x + 1, y − 1),
(x − 1, y + 1), (x − 1, y − 1)}

36. Alguns relacionamentos b´asicos entre pixels
Vizinhos de um pixel
Dado um pixel p de coordenadas (x, y)...
Vizinhanc¸a-4 de p:
N4(p) :
{(x +1, y), (x −1, y), (x, y +1), (x, y −1)}
Vizinhanc¸a diagonal de p:
Nd (p) :
{(x + 1, y + 1), (x + 1, y − 1),
(x − 1, y + 1), (x − 1, y − 1)}
vizinhanc¸a-8 de p:
N8(p) : {N4(p) ∪ Nd (p)}

37. Alguns relacionamentos b´asicos entre pixels
Para explicarmos melhor os pr´oximos conceitos, considere a
seguinte matrix que representa uma imagem bin´aria:









0 1 1 1 0
0 1 0 1 1
1 0 0 0 0
0 1 1 0 0
1 0 0 1 0
1 1 1 0 0










38. Alguns relacionamentos b´asicos entre pixels
Adjacˆencia
p e q tˆem adjacˆencia-4 se: q ∈ N4(p)
p e q tˆem adjacˆencia-8 se: q ∈ N8(p)
p e q tˆem adjacˆencia-m se:
{q ∈ N4(p)} ou {q ∈ Nd (p)}e{N4(p) ∩ N4(q) = ∅}
Observac¸˜ao
A adjacˆencia mista foi criada para eliminar as ambiguidades que
muitas vezes surgem com a utilizac¸˜ao da adjacˆencia-8.

39. Alguns relacionamentos b´asicos entre pixels
Caminho (ou curva) entre pixels
Caminho digital do pixel p com coordenadas (s1, t1) ao pixel q
com coordenadas (s2, t2):
(x0, y0), (x1, x1), ..., (xn, yn)
onde (x0, y0 = (s1, t1) e (xn, yn) = (s2, t2).
Os pixels (xi , yi ) e (xi−1, yi−1) s˜ao adjacentes para 1 ≤ i ≤ n.
Se (x0, y0) = (xn, yn), o caminho ´e dito fechado.
Podemos definir caminhos-4, -8 ou -m dependendo do tipo de
adjacˆencia especificada.

40. Alguns relacionamentos b´asicos entre pixels
Conectividade
S ´e um subconjunto de pixels em uma imagem.
Dois pixels p e q s˜ao conexos em S se houver um caminho
entre eles consistindo inteiramente de pixels em S.
∀p ∈ S, o conjunto de pixels em S que s˜ao conectados a ele ´e
chamado de componente conexo de S.
Se existir apenas um componente conexo, o conjunto S ´e
chamado de um conjunto conexo.

41. Alguns relacionamentos b´asicos entre pixels
Regi˜oes
R representando um subconjunto de pixels na imagem, R ´e
uma regi˜ao da imagem, se R for um conjunto conexo.
Duas regi˜oes Ri e Rj s˜ao consideradas adjacentes se sua uni˜ao
formar um conjunto conexo.
Regi˜oes que n˜ao s˜ao adjacentes s˜ao disjuntas.
Observac¸˜ao
Consideramos adjacˆencia-4 e -8 ao nos referirmos a regi˜oes...

42. Alguns relacionamentos b´asicos entre pixels
Regi˜oes
Suponha que uma imagem contenha k regi˜oes disjuntas Rk,
k = 1, 2, ...K.
Ru = R1 ∪ R2 ∪ R3 ∪ ... ∪ RK .
(Ru)c
´e o complemento de Ru
Todos os pontos em Ru: foreground da imagem
Todos os pontos em (Ru)c: background da imagem.

43. Alguns relacionamentos b´asicos entre pixels
Fronteira
Conjunto de pontos em R adjacentes aos pontos de Rc.
Observac¸˜ao
Mais uma vez: Devemos considerar a adjacˆencia usada para definir
a conectividade!

44. Alguns relacionamentos b´asicos entre pixels
Bordas vs Fronteiras
Existe uma
importante diferenc¸a
entre esses conceitos
Bordas s˜ao formadas
por pixels com valores
cujas derivadas
excedem um limiar
pr´e-definido. (Mais
na frente, quando
falarmos sobre
segmentac¸˜ao
entenderemos isso
melhor...)

45. Alguns relacionamentos b´asicos entre pixels
Medidas de distˆancias
Para pixels p, q e z com coordenadas (x, y), (s, t) e (v, w),
respectivamente. D ´e uma func¸˜ao de distˆancia se:
D(p, q) ≥ 0 D(p, q) = 0 se p = q
D(p, q) − D(q, p)
D(p, z) ≤ D(p, q) + D(q, z)

46. Alguns relacionamentos b´asicos entre pixels
Medidas de distˆancias - Exemplos
De(p, q) = [(x − s)2
+ (y − t)2
]( 1
2
)
De(p, q) = [(x − s)2 + (y − t)2]( 1
2
)
D4(p, q) =| x − s | + | y − t |D4(p, q) =| x − s | + | y − t |
Ds (p, q) = max(| x − s |, | y − t |)Ds (p, q) = max(| x − s |, | y − t |)

47. Algumas ferramentas matem´aticas importantes
Operac¸˜oes de arranjo espacial vs matrizes
Suponhamos duas imagens A e B:
A =
a1,1 a1,2
a2,1 a2,2
B =
b1,1 b1,2
b2,1 b2,2
Produto do arranjo matricial dessas duas imagens:
a1,1 a1,2
a2,1 a2,2
b1,1 b1,2
b2,1 b2,2
=
a1,1b1,1 a1,2b1,2
a2,1b2,1 a2,2b2,2
Produto de matrizes:
a1,1 a1,2
a2,1 a2,2
b1,1 b1,2
b2,1 b2,2
=
a1,1b1,1 + a1,2b2,1 a1,1b1,2 + a1,2b2,2
a2,1b1,1 + a2,2b2,1 a2,1b1,2 + a2,2b2,2

48. Algumas ferramentas matem´aticas importantes
Operac¸˜oes aritm´eticas entre imagens
S˜ao operac¸˜oes de arranjo espacial...
s(x, y) = f (x, y) + g(x, y)
d(x, y) = f (x, y) − g(x, y)
p(x, y) = f (x, y) × g(x, y)
v(x, y) = f (x, y) ÷ g(x, y)

49. Algumas ferramentas matem´aticas importantes
Operac¸˜oes aritm´eticas entre imagens
Imagem corrompida por ru´ıdo:
g(x, y) = f (x, y) + η(x, y)
Realc¸e utilizando subtrac¸˜ao de
imagens

50. Algumas ferramentas matem´aticas importantes
Operac¸˜oes b´asicas com conjuntos
Os elementos de uma imagem em escala de cinza s˜ao
representados pelo conjunto A cujos elementos s˜ao expressos em
um grupo de trˆes vari´aveis (x, y, z)...
Negativo de A: Ac = {x, y, 255 − z}|(x, y, z) ∈ A}
Uni˜ao de A com B: A ∪ B = {maxz(a, b)|a ∈ A, b ∈ B}

51. Algumas ferramentas matem´aticas importantes
Operac¸˜oes l´ogicas

52. Algumas ferramentas matem´aticas importantes
Operac¸˜oes espaciais
Operac¸˜ao ponto a ponto
s = T(z)

53. Algumas ferramentas matem´aticas importantes
Operac¸˜oes espaciais
Operac¸˜ao ponto a ponto
s = T(z)
Operac¸˜ao por vizinhanc¸a
g(x, y) = 1
mn
(r,c)∈Sxy
f (r, c)

54. Algumas ferramentas matem´aticas importantes
Operac¸˜oes espaciais
Operac¸˜ao ponto a ponto
s = T(z)
Operac¸˜ao por vizinhanc¸a
g(x, y) = 1
mn
(r,c)∈Sxy
f (r, c)
Transformac¸˜oes
geom´etricas
(x, y) = T{(v, w)}

55. Algumas ferramentas matem´aticas importantes
Transformadas
Em alguns casos, tarefas de PI s˜ao mais bem formuladas trasnformando
as imagens de entrada, transferindo a tarefa especificada para o dom´ınio
da transformada e aplicando a transformada inversa para retornar ao
dom´ınio espacial...
T(x, y) =
M−1
x=0
N−1
y=0
f (x, y)r(x, y, u, v)
f (x, y) =
M−1
x=0
N−1
y=0
T(x, y)s(x, y, u, v)

56. Algumas ferramentas matem´aticas importantes
Operac¸˜oes com vetores e matrizes

57. Algumas ferramentas matem´aticas importantes
M´etodos probabil´ısticos
Probabilidade de n´ıveis e intensidade zk ocorrerem... p(zk ) = nk
MN
Intensidade m´edia... m =
L−1
k=0
zk p(zk )
Variˆancia de intensidades... σ2
=
L−1
k=0
(zk − m)n
p(zk )

58. Por hoje, ficamos por aqui.