Este documento apresenta um programa sobre a Semana da Computação da UFJF que inclui informações preliminares, conteúdo sobre a linguagem R, análise de casos e interface com outras linguagens. O documento discute a filosofia e objetivos do R, como invocar o R na linha de comando, sintaxe básica incluindo vetores, caracteres e números, e estruturas de dados.









![Invocando o R na linha de comando
Ajuda sobre algo sobre o que se deseja
1> apropos('help') # busca por comandos similares
2> [1] "help" "help.request" "help.search" "help.start"
3> apropos('mean')
4> [1] "colMeans" "kmeans" "mean"
5> [5] "mean.Date" "mean.default" "mean.difftime"
6> [9] "mean.POSIXlt" "rowMeans" "weighted.mean"
Quando só se sabe o que procurar
1> help('mean') # help em modo texto
2> ?mean # o mesmo que help('mean')
3> help('mean',help_type='html') # help em modo html
11 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-13-320.jpg)
![Invocando o R na linha de comando
Para sair do programa, digite
1> quit()
2> Save workspace image? [y/n/c]: n
12 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-14-320.jpg)

![Informações Preliminares
Funcionamento básico:
entre com uma expressão no console e digite <enter>
a expressão é avaliada e o resultado impresso na tela
Note que [1] sempre acompanha qualquer resultado
1 # Isto éum comentário
2 1 + 2 + 3
3 [1] 6
4 1 + 2 * 3 # outro comentário
5 [1] 7
6 (1 + 2) * 3 # ...
7 [1] 9
13 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-16-320.jpg)
![Informações Preliminares
R é case-sensitive: então A e a são símbolos diferentes e se referem
a diferentes variáveis
Comandos são separados por ponto e vírgula “;”
O conjunto de símbolos dependem do idioma e do sistema
operacional onde se roda o R (tecnicamente, o locale em uso)
Todos os símbolos alfanuméricos são permitidos, incluindo “.” e “_”
Comentários começam com “#”
1 #
2 A=2; a=banana
3 print(A)
4 [1] 2
5 print(a)
6 [1] banana
7 #
8 .num=45; print(.num+1)
9 [1] 46
14 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-17-320.jpg)
![Informações Preliminares
Como a maioria das linguagens de programação, R permite atribuir
valores a variáveis
A operação de atribuição tem a sintaxe objeto recebe valor
Há dois operadores que atribuem valores a um objeto dessa maneira
sinal de menor seguido de hífen: -
sinal de igual: =
1 # Os dois operadores de atribuição - e = são equivalentes
2 a - 2
3 f - b = 5*a
4 print(a)
5 [1] 2
6 print(b)
7 [1] 10
8 print(f)
9 [1] 10
15 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-18-320.jpg)
![Informações Preliminares
Uma forma de atribuição menos usada é valor atribuído a objeto
1 # Outra forma, menos usual é
2 salsa -d -e
3 print(d)
4 [1] salsa
5 print(e)
6 [1] salsa
7
8 # Para saber mais
9 ?=
10 ?-
16 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-19-320.jpg)
![Informações Preliminares
Em R, todo resultado é interpretado como um vetor
O “[1]” indica o índice do vetor
No caso abaixo, os números entre colchetes indicam o índice do
primeiro elemento de cada linha
1 # sequência de inteiros no intervalo [1,50]
2 1:50
3 [1] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
4 [23] 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41
5 [42] 42 43 44 45 46 47 48 49 50
17 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-20-320.jpg)
![Informações Preliminares
1 # Usando o R como calculadora
2 4+6
3 [1] 10
4 2+3*4
5 [1] 14
6 3/2+1
7 [1] 2.6
8 4*3**3 # potências são indicadas por ** ou ^
9 [1] 108
10
11 # Outras funções
12 sqrt(2)
13 [1] 1.414214
14 sin(pi) # os ângulos são interpretados em radianos
15 [1] 1.224606e-16 # zero!
16 sqrt(sin(45*pi/180))
17 [1] 0.8408964
18 log(1) # logaritmo neperiano (base e)
19 [1] 0
20 log(64,4) # base 4
21 [1] 3
18 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-21-320.jpg)

![Sintaxe do R
Vetores numéricos
1 # Números são interpretados literalmente
2 1.1
3 [1] 1.1
4 2^1023
5 [1] 8.988466e+307
6
7 # Valores em notação hexadecimal comecam com 0x
8 0x1
9 [1] 1
10 0xFFFF
11 [1] 65535
12
13 # Qualquer número éinterpretado como ponto flutuante de dupla precisão
14 typeof(1)
15 [1] double
16 ?typeof # mais sobre a função typeof()
17 typeof(as(1,integer)) # se deseja um inteiro, use a função as
18 [1] integer
20 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-24-320.jpg)
![Sintaxe do R
Vetores numéricos
1 # Limites de precisão
2 (2^1023 + 1) == 2^1023 # 2^1023 éo máximo de precisão
3 [1] TRUE
4 # Limites de tamanho
5 2^1024
6 [1] Inf # o universo so existe até 2^1023
7
8 # R suporta complexos, escritos como (real) + (imaginário)i
9 0+1i ^ 2
10 [1] -1+0i
11 sqrt(-1+0i)
12 [1] 0+1i
13 exp(0+1i * pi)
14 [1] -1+0i
15
16 # A função sqrt() retorna um valor do mesmo tipo de entrada
17 sqrt(-1)
18 [1] NaN
19 Warning message:
20 In sqrt(-1) : NaNs produced
21 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-25-320.jpg)
![Sintaxe do R
Vetores numéricos
1 # O operador a:b retorna uma sequência de inteiros no intervalo [a,b]
2 1:5
3 [1] 1 2 3 4 5
4 typeof(1:5)
5 [1] integer
6
7 # Para combinar um conjunto de números em um vetor, use a função c()
8 v - c(173,12,1.12312,-93)
9 print(v)
10 [1] 173.00000 12.00000 1.12312 -93.0000000
11
12 # Em R, c se refere a função primitiva c(), porém você pode redefinitr c
13 c - 3
14 c
15 [1] 3
16 # mesmo após redefinir c, você pode combinar números
17 v - c(3,2,1)
18 v
19 [1] 3 2 1
22 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-26-320.jpg)
![Sintaxe do R
Caracteres
1 # Um caracter contém texto entre duas aspas
2 y - abc
3 y
4 [1] abc
5 length(y) # tamanho de y
6 [1] 1
7 mode(y) # equivalente a typeof()
8 [1] character
9
10 # Um vetor de caracteres
11 z - c(abc,29 88)
12 length(z)
13 [1] 2
14 mode(z)
15 [1] character
23 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-27-320.jpg)
![Sintaxe do R
Caracteres
1 # Concatenação de caracteres ...
2 u - paste(abc,de,f) # concatena as strings
3 u
4 [1] abc de f
5 # ... e separação (split)
6 v - strsplit(u,.) # divide em função dos espaços
7 v
8 [[1]]
9 [1] abc de f
10
11 # Outra forma de concaternar ...
12 u - paste(abc,de,f,sep=.) # usa . como separador
13 u
14 [1] abc.de.f
15 # ... e separar
16 strsplit(u,)
17 [[1]]
18 [1] a b c . d e . f
24 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-28-320.jpg)
![Símbolos
Um símbolo é um objeto que se refere a outro objeto
1 # Símbolo éo nome da variável em R
2 x1 - 1
3 X1 - 2
4 x1
5 [1] 1
6 X1
7 [1] 2
8 x1.1 - 1
9 x1.1_1 - 1
10
11 # Se necessário (!?), defina um símbolo assim:
12 1+2=3 - hello
13 1+2=3
14 [1] hello
15
16 # Nem todas as palavras são símbolos (palavras reservadas)
17 # -- if, else, repeat, while, function, for, in, next, break
18 # -- TRUE, FALSE, NULL, Inf, NaN, NA
19 # -- ...
25 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-30-320.jpg)
![Símbolos
Funções
Uma função é uma outra forma de atribuir valor a um símbolo
1 # Atribui a função vetorial c(x+1, y+1) ao símbolo f
2 f - function(x,y) {c(x+1, y+1)}
3 f(1,2)
4 [1] 2 3
5 # Para visualizar o conteúdo de f
6 f
7 function(x,y) {c(x+1, y+1)}
8
9 # Visualizando o conteúdo da função desvio padrão
10 sd
11 function (x, na.rm = FALSE)
12 {
13 if (is.matrix(x))
14 apply(x, 2, sd, na.rm = na.rm)
15 else if (is.vector(x))
16 sqrt(var(x, na.rm = na.rm))
17 else if (is.data.frame(x))
18 sapply(x, sd, na.rm = na.rm)
19 else sqrt(var(as.vector(x), na.rm = na.rm))
20 }
26 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-31-320.jpg)
![Vetores
Operações básicas
O comando c(), de “combinar” é a forma principal de criar vetores
1 # Criando objetos
2 x- c(1,2,3); print(x)
3 [1] 1 2 3
4 y- 5:9; print(y) # aqui temos uma sequência
5 [1] 5 6 7 8 9
6 z-c(x,y); print(z) # x e y são aglutinados em z
7 [1] 1 2 3 5 6 7 8 9
8
9 # Listando os elementos no espaço de trabalho
10 ls()
11 [1] x y z
12
13 # Apagando alguns deles
14 rm(x,y)
15
16 # Listando novamente
17 ls()
18 [1] z
19
20 rm(list=ls()) # apaga tudo
27 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-33-320.jpg)
![Vetores
Operações básicas
1 # soma de vetores
2 c(1,2,3) + c(1,1,1)
3 [1] 2 3 4
4 # se não têm o mesmo tamanho, a menor sequência érepetida
5 c(1, 2, 3, 4) + 1
6 [1] 2 3 4 5
7
8 # o mesmo vale para divisão
9 1 / c(1, 2, 3, 4, 5)
10 [1] 1.0000000 0.5000000 0.3333333 0.2500000 0.2000000
11
12 # no caso abaixo, a menor sequência tem tamanho 2
13 c(1, 2, 3, 4) + c(10, 100)
14 [1] 11 102 13 104
15
16 # a primeira sequência não émúltipla da segunda: 5 não émútiplo de 2
17 c(1, 2, 3, 4, 5) + c(10, 100)
18 [1] 11 102 13 104 15
19 Mensagens de aviso perdidas:
20 In c(1, 2, 3, 4, 5) + c(10, 100) :
21 comprimento do objeto maior não émúltiplo do comprimento do objeto menor
28 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-34-320.jpg)
![Vetores
Operações básicas
1 # Em R podemos entrar com expressões de caracteres
2 Hello world.
3 [1] Hello world.
4
5 # Um vetor de caracteres de comprimento 3
6 c(Hello world, Hello R interpreter)
7 [1] Hello world
8 Hello R interpreter
29 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-35-320.jpg)
![Vetores
Operações básicas
1 # Formas de acessar os membros de um vetor
2 b = c(1:10)
3 b
4 [1] 1 2 3 4 5 6 7 8 9 10
5 b[5] # acessa o 5o. elemento de b
6 [1] 5
7 b[2:7] # acessa uma fatia de b
8 [1] 2 3 4 5 6 7
9 b%%3 # resto da divisão por 3
10 [1] 1 2 0 1 2 0 1 2 0 1
11
12 # A operação abaixo retorna um vetor lógico
13 b%%3==0
14 [1] FALSE FALSE TRUE FALSE FALSE TRUE FALSE FALSE TRUE FALSE
15
16 # Elementos de b congruentes de 0 (mod 3)
17 b[b%%3==0]
18 [1] 3 6 9
19 #
20 b[c(2,6,9)]
21 [1] 2 6 9
30 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-36-320.jpg)
![Instruções de Controle
As instruções de controle em R são muito similares àquelas de C,
C++, Perl e Python
Aqui vamos focar nos laços (loops) e condicionais (if-else)
1 # Python-like for: uma iteração para cada elemento
2 x - c(5,12,13)
3 for (n in x){
4 + y = x/10
5 + print(n^2+y)
6 + }
7 [1] 25.5
8 [1] 144.12
9 [1] 169.13
10
11 # O mesmo vale para listas
12 l=list(p=21,k=c(1,2,3),z=NaN, f=function(a){return(a^2)})
13 for(x in l) print(x)
14 [1] 21
15 [1] 1 2 3
16 [1] NaN
17 function(a){return(a^2)}
31 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-38-320.jpg)
![Instruções de Controle
1 # C-style while
2 i - 1
3 while (i = 10) i - i+4
4 i
5 [1] 13
6
7 # Funcionamento básico do if
8 if (r == 4) {
9 + x - 1
10 +} else {
11 + x - 3
12 + y - 4
13 +}
14
15 # Duas formas de representar a mesma operação
16 x - 1
17 y - if(x == 2) x else x+1
18 y
19 [1] 2
20 if(x == 2) y - x else y - x+1
21 y
22 [1] 2
32 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-39-320.jpg)
![Funções
Em R, as operações que fazem todo o trabalho são chamadas
funções
1 # Funções com 1 argumento
2 exp(1)
3 [1] 2.718282
4 cos(3.141593)
5 [1] -1
6
7 # Alguns argumentos podem ser especificados pelo nome
8 log(x=64, base=4)
9 [1] 3
10
11 # O comando seq() possui vários argumento opcionais
12 seq(from=0,to=10,by=0.8) # intervalo
13 [1] 0.0 0.8 1.6 2.4 3.2 4.0 4.8 5.6 6.4 7.2 8.0 8.8 9.6
14 seq(from=0,to=10,length=20) # comprimento
15 [1] 0.0000000 0.5263158 1.0526316 1.5789474 2.1052632 2.6315789
16 [7] 3.1578947 3.6842105 4.2105263 4.7368421 5.2631579 5.7894737
17 [13] 6.3157895 6.8421053 7.3684211 7.8947368 8.4210526 8.9473684
18 [19] 9.4736842 10.000000
33 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-41-320.jpg)
![Funções
Nem todas as funções têm a forma f (x1,x2,....)
Algumas aparecem na forma de operadores
1 17 + 2
2 [1] 19
3 2 ^ 10
4 [1] 1024
5 3 == 4
6 [1] FALSE
34 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-42-320.jpg)
![Funções
Assim como em qualquer linguagem de programação, o cerne do R
consiste em escrever funções
Uma função é um grupo de instruções que recebe as entradas, opera
sobre elas e retorma uma saída
1 # Conta o número de números ímpares em um vetor de inteiros
2 oddcount - function(x)
3 + k - 0 # o + indica continuação de linha
4 + for (n in x) {
5 + if (n %% 2 == 1) k
6 + }
7 + return(k) # o função retorna alguma coisa
8 + }
9
10 oddcount(c(1,3,5))
11 [1] 3
12 oddcount(c(1,2,3,7,9))
13 [1] 4
35 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-43-320.jpg)
![Funções
Variáveis criadas fora da função são globais e visíveis pela função
1 f - function(x) return(x+y)
2 y - 3
3 f(5)
4 [1] 8
Entradas podem ter um valor default
1 f - function(x,y=10) return(x+y)
2 f(x=3)
3 [1] 13
4 f(x=3,y=3)
5 [1] 6
6 f(k=3)
7 Error in f(k = 3) : unused argument(s) (k = 3)
36 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-44-320.jpg)
![Operadores
Operadores básicos
Um operador é uma função que toma um ou mais argumentos e
pode ser escrita sem parênteses
1 x - -1:5
2 x
3 [1] -1 0 1 2 3 4 5
4
5 # adição e multiplicação
6 2 * x + 3
7 [1] 1 3 5 7 9 11 13
8 # exponenciação
9 x^3
10 [1] -1 0 1 8 27 64 125
11
12 # resto da divisão (módulo)
13 x %% 2 #-- éperiódico
14 [1] 1 0 1 0 1 0 1
15
16 # divisão inteira
17 x %/% 5 # x %/% 5 == floor(x/5)
18 [1] -1 0 0 0 0 0 1
37 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-46-320.jpg)
![Operadores
Operadores definidos pelo usuário
1 # Você pode definir seus próprios operadores
2 # Vamos definir o operador %myop% através de uma função
3
4 %myop% - function(a, b) {2*a + b}
5 1 %myop% 1
6 [1] 3
7 1 %myop% 2
8 [1] 4
9
10 c(1,2,3,4,5) %myop% 2
11 [1] 4 6 8 10 12
12
13 # Atribuição éum operador
14 x - c(1,2,3,4,5)
15
16 # O negativo também éum operador
17 -7
18 [1] -7
19
20 # O ponto de interrogação ? (help) também éum operador
21 ??
38 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-47-320.jpg)
![Operadores
Atribuição
1 # As operações de atribuição atribuem um objeto a um símbolo
2
3 # Vetor atribuído a um símbolo
4 v - c(1,2,3,4,5,6,7,8)
5
6 # Objeto lista atribuída a um símbolo
7 y - list(sapato=mocassim, chapeu=gorro, camisa=polo)
8 y
9 $sapato
10 [1] mocassim
11
12 $chapeu
13 [1] gorro
14
15 $camisa
16 [1] polo
17
18 # Objeto função atribuído a um símbolo
19 z - function(a,b,c) {a ^ b / c}
20 z
21 function(a,b,c) {a ^ b / c}
39 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-48-320.jpg)

![Estruturas de dados
Arrays
1 # Um array éum vetor multidimensional
2 a - array(c(1,2,3,4,5,6,7,8,9,10,11,12),dim=c(3,4))
3 a
4 [,1] [,2] [,3] [,4]
5 [1,] 1 4 7 10
6 [2,] 2 5 8 11
7 [3,] 3 6 9 12
8 # Para acessar o elemento [2,2]
9 a[2,2]
10 [1] 5
11 # Veja como fica um vetor com o mesmo conteúdo
12 v - c(1,2,3,4,5,6,7,8,9,10,11,12); v
13 [1] 1 2 3 4 5 6 7 8 9 10 11 12
41 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-51-320.jpg)
![Estruturas de dados
Arrays
1 # Relembrando do array a, podemos acessá-lo de diferentes formas
2 a
3 [,1] [,2] [,3] [,4]
4 [1,] 1 4 7 10
5 [2,] 2 5 8 11
6 [3,] 3 6 9 12
7
8 # Somente a primeira linha
9 a[1,]
10 [1] 1 4 7 10
11 # Somente a primeira coluna
12 a[,1]
13 [1] 1 2 3
14
15 # Acessando uma fatia das linhas
16 a[1:2,]
17 [,1] [,2] [,3] [,4]
18 [1,] 1 4 7 10
19 [2,] 2 5 8 11
42 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-52-320.jpg)
![Estruturas de dados
Arrays
1 # Relembrando do array a mais uma vez
2 a
3 [,1] [,2] [,3] [,4]
4 [1,] 1 4 7 10
5 [2,] 2 5 8 11
6 [3,] 3 6 9 12
7
8 # Acessando um conjunto não contíguo colunas
9 a[,c(1,3)] # mostra somente as colunas 1 e 3
10 [,1] [,2]
11 [1,] 1 7
12 [2,] 2 8
13 [3,] 3 9
14
15 # O sinal negativo exclui linhas ou colunas
16 a[-c(1,3),] # exclui linhas 1 e 3
17 [1] 2 5 8 11
18 a[-2,-c(1,4)] # exclui linha 2 e colunas 1 e 4
19 [,1] [,2]
20 [1,] 4 7
21 [2,] 6 9
43 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-53-320.jpg)
![Estruturas de dados
Arrays
1 # Uma matriz éum array bidimensional
2 m - matrix(data=c(1,2,3,4,5,6,7,8,9,10,11,12),nrow=3,ncol=4)
3 m
4 [,1] [,2] [,3] [,4]
5 [1,] 1 4 7 10
6 [2,] 2 5 8 11
7 [3,] 3 6 9 12
8
9 # O comando matrix(() preenche as colunas com os dados fornecidos
10 matrix(1:6,nrow=2)
11 [,1] [,2] [,3]
12 [1,] 1 3 5
13 [2,] 2 4 6
14
15 # O preencimento por linhas também épossível
16 matrix(1:6,nrow=2, byrow=TRUE)
17 [,1] [,2] [,3]
18 [1,] 1 2 3
19 [2,] 4 5 6
44 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-54-320.jpg)
![Estruturas de dados
Arrays
1 # Uma outra forma de criar uma matriz éusando as funções
2 # -- rbind()
3 m - rbind(c(1,4),c(2,-3))
4 m
5 [,1] [,2]
6 [1,] 1 4
7 [2,] 2 -3
8
9 # -- cbind()
10 n - cbind(c(1,4),c(2,-3))
11 n
12 [,1] [,2]
13 [1,] 1 2
14 [2,] 4 -3
15
16 # --diag()
17 diag(2)
18 [,1] [,2]
19 [1,] 1 0
20 [2,] 0 1
45 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-55-320.jpg)
![Estruturas de dados
Arrays
1 # Além da soma e subtração, temos as operações
2 # -- multiplicação termo a termo
3 m * diag(2)*3
4 [,1] [,2]
5 [1,] 3 0
6 [2,] 0 -9
7
8 # -- divisão termo a termo
9 m/diag(2)
10 [,1] [,2]
11 [1,] 1 Inf
12 [2,] Inf -3
13
14 # -- produto matricial
15 m % * % n
16 [,1] [,2]
17 [1,] 17 -10
18 [2,] -10 13
46 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-56-320.jpg)
![Estruturas de dados
Arrays
Atenção!
1 # O R pode operar com arrays de diferentes tamanhos, por conta do reuso dos vetores!
2 x=matrix(1:6,ncol=2)
3 x
4 [,1] [,2]
5 [1,] 1 4
6 [2,] 2 5
7 [3,] 3 6
8
9 # Aparentemente, a operação não faria sentido
10 x+c(1,2)
11 [,1] [,2]
12 [1,] 2 6
13 [2,] 4 6
14 [3,] 4 8
15
16 # Vamos vamos fazer algumas considerações...
47 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-57-320.jpg)
![Estruturas de dados
Arrays
Atenção!
1 # Neste caso, ocorre a repetição dos valores, e a soma anterior éequivalente a
2 x + c(1,2,1,2,1,2)
3 [,1] [,2]
4 [1,] 2 6
5 [2,] 4 6
6 [3,] 4 8
7
8 # Observe a construção da matrix y, com c(1,2) repetido nas colunas
9 y=matrix(c(1,2,1,2,1,2),ncol=2)
10 y
11 [,1] [,2]
12 [1,] 1 2
13 [2,] 2 1
14 [3,] 1 2
15 x + y
16 [,1] [,2]
17 [1,] 2 6
18 [2,] 4 6
19 [3,] 4 8
48 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-58-320.jpg)
![Estruturas de dados
Arrays
1 # Arrays podem ter mais de uma dimensão
2 w - array(c(1:18),dim=c(3,3,2))
3 print(w)
4 , , 1
5
6 [,1] [,2] [,3]
7 [1,] 1 4 7
8 [2,] 2 5 8
9 [3,] 3 6 9
10
11 , , 2
12
13 [,1] [,2] [,3]
14 [1,] 10 13 16
15 [2,] 11 14 17
16 [3,] 12 15 18
17
18 # Acessando um dos elementos
19 w[1,1,1]
20 [1] 1
49 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-59-320.jpg)
![Estruturas de dados
Listas
Uma lista aceita a mistura de objetos de diferentes tipos
1 # Uma lista contendo um número e uma string
2 e - list(elemento=esfera, raio=8.25)
3 e
4 $elemento
5 [1] esfera
6
7 $raio
8 [1] 8.25
9
10 # Os objetos podem ser acessados de várias formas
11 e$elemento
12 [1] esfera
13 e[2]
14 $raio
15 [1] 8.25
16
17 e[[2]]
18 [1] 8.25
50 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-60-320.jpg)
![Estruturas de dados
Listas
1 # Uma lista pode referenciar outra lista
2 g - list(Essa lista referencia outra lista, e)
3 g
4 [[1]]
5 [1] Essa lista referencia outra lista
6
7 [[2]]
8 [[2]]$objeto
9 [1] esfera
10
11 [[2]]$raio
12 [1] 8.25
51 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-61-320.jpg)
![Estruturas de dados
Dataframes
Um dataframe é um objeto que contém múltiplos vetores que são do
mesmo tamanho
é semelhante a uma planilha ou base de dados
bons para representar dados experimentais
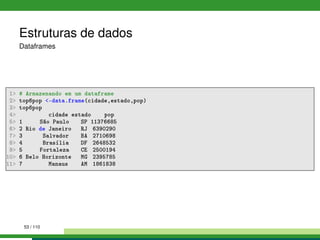
1 # As 6 cidades mais populosas do Brasil
2 cidade - c('São Paulo','Rio de Janeiro','Salvador','Brasília','Fortaleza', 'Belo ←
Horizonte','Manaus')
3 estado - c('SP','RJ','BA','DF','CE','MG','AM')
4 pop - c(11376685,6390290,2710698,2648532,2500194,2395785,1861838)
5
6 # As informações estão armazenadas em vetores
7 cidade
8 [1] São Paulo Rio de Janeiro Salvador Brasília
9 [5] Fortaleza Belo Horizonte Manaus
10 estado
11 [1] SP RJ BA DF CE MG AM
12 pop
13 [1] 11376685 6390290 2710698 2648532 2500194 2395785 1861838
52 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-62-320.jpg)
![Estruturas de dados
Dataframes
1 # Acessando as informações contidas em top6pop
2 top6pop$estado
3 [1] SP RJ BA DF CE MG AM
4 Levels: AM BA CE DF MG RJ SP
5 #
6 top6pop[2] # outra forma de acessar os estados
7 estado
8 1 SP
9 2 RJ
10 3 BA
11 4 DF
12 5 CE
13 6 MG
14 7 AM
15 #
16 top6pop$pop 2.7e6 # cidades com mais de 2.7 mi hab
17 [1] TRUE TRUE TRUE FALSE FALSE FALSE FALSE
18 #
19 top6pop$pop[top6pop$pop2.7e6] # populações maiores que 2.7 mi hab
20 [1] 11376685 6390290 2710698
54 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-64-320.jpg)
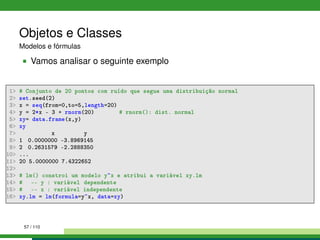
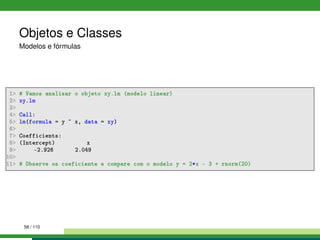
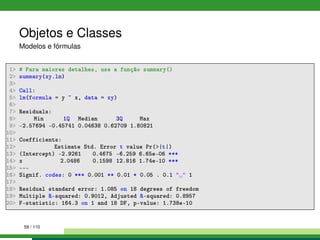
![Objetos e Classes
R é uma linguagem orientada a objetos
Cada objeto em R tem um tipo
E cada objeto em R é membro de uma classe
Já encontramos diferentes classes: vetores de caracteres, vetores
numéricos, dataframes, listas, ...
1 class(1:10)
2 [1] integer
3 class(w)
4 [1] array
5 class(v)
6 [1] numeric
7 class(top6pop)
8 [1] data.frame
9 class(e)
10 [1] list
11 class(class)
12 [1] function
55 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-66-320.jpg)

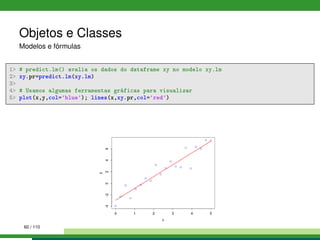

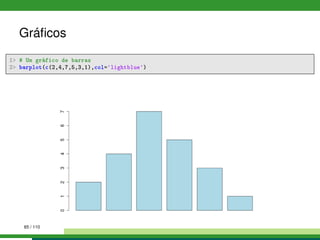
![Gráficos
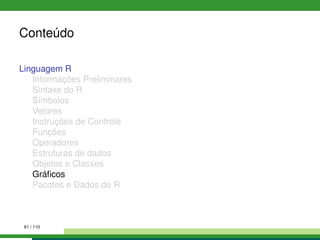
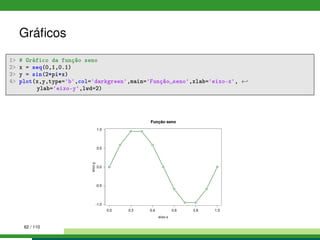
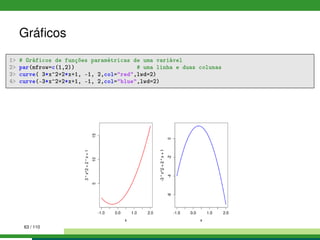
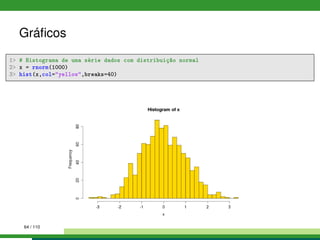
1 # Gráfico de pizza
2 pie(1:6, col = rainbow(6), labels= LETTERS[1:6], radius = 0.9)
66 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-78-320.jpg)
![Pacotes e Dados do R
Dados
1 # Para acessar um determinado conteúdo
2 data(trees)
3 trees
4 Girth Height Volume
5 1 8.3 70 10.3
6 2 8.6 65 10.3
7 ...
8 31 20.6 87 77.0
9
10 # Operando com os dados
11 class(trees)
12 [1] data.frame
13 mean(trees)
14 Girth Height Volume
15 13.24839 76.00000 30.17097
16 str(trees) # mostra informações sobre a estrututa do objeto
17 'data.frame': 31 obs. of 3 variables:
18 $ Girth : num 8.3 8.6 8.8 10.5 10.7 10.8 11 11 11.1 11.2 ...
19 $ Height: num 70 65 63 72 81 83 66 75 80 75 ...
20 $ Volume: num 10.3 10.3 10.2 16.4 18.8 19.7 15.6 18.2 22.6 19.9 ...
70 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-83-320.jpg)
![Pacotes e Dados do R
Dados
1 # Medidas do fluxo anual do Nilo na cidade de Ashwan 1871-1970
2 data(Nile)
3 Nile
4 Time Series:
5 Start = 1871
6 End = 1970
7 Frequency = 1
8 [1] 1120 1160 963 1210 1160 1160 813 1230 1370 1140 995 935
9 [13] 1110 994 1020 960 1180 799 958 1140 1100 1210 1150 1250
10 [25] 1260 1220 1030 1100 774 840 874 694 940 833 701 916
11 [37] 692 1020 1050 969 831 726 456 824 702 1120 1100 832
12 [49] 764 821 768 845 864 862 698 845 744 796 1040 759
13 [61] 781 865 845 944 984 897 822 1010 771 676 649 846
14 [73] 812 742 801 1040 860 874 848 890 744 749 838 1050
15 [85] 918 986 797 923 975 815 1020 906 901 1170 912 746
16 [97] 919 718 714 740
17 str(Nile)
18 Time-Series [1:100] from 1871 to 1970: 1120 1160 963 1210 1160 1160 813 1230 1370 ←
1140 ...
19 class(Nile) # objeto time series (série temporal)
20 [1] ts
71 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-84-320.jpg)

![Pacotes e Dados do R
Pacotes
1 # Pacotes carregados automaticamente
2 getOption(defaultPackages)
3 [1] datasets utils grDevices graphics methods stats
4
5 # Pacotes disponíveis para serem carregados
6 (.packages(all.available=TRUE))
7 [1] ade4 calibrate clusterSim corrgram
8 [6] Defaults ellipse gclus Hmisc
9 [11] nutshell quantmod R2HTML RColorBrewer
10 [16] seriation TSP TTR xts
11 [21] ape biclust bitops cba
12 [26] colorspace dataframes2xls e1071 emoa
13
14 # Instalação de pacotes -- repositórios online
15 install.packages('psy')
16
17 # Remoção de pacotes
18 remove.packages(c(tree, maptree),.Library)
74 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-87-320.jpg)
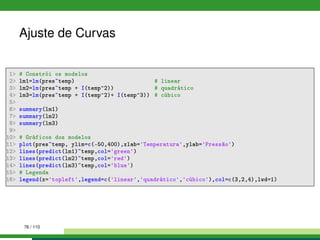
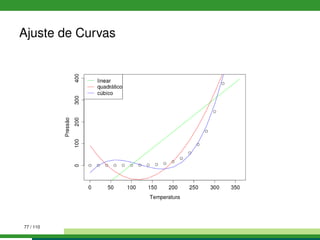

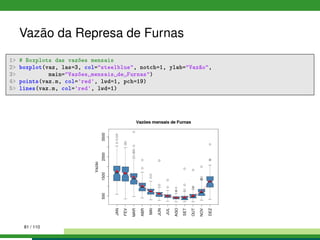
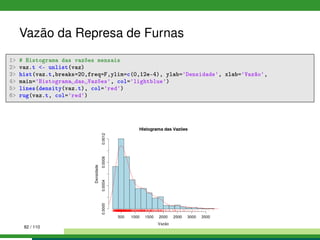
![Vazão da Represa de Furnas
1 #
2 # Análise da série histórica das vazões mensais da barragens de Furnas
3 # Fonte: http://www.ons.org.br/operacao/vazoes_naturais.aspx
4 #
5 rm(list=ls()) # apaga todo o workspace
6 print(getwd()) # onde estamos?
7
8
9 # Dados das vazões na planilha
10 # Vazoes_Mensais_1931_2010.xls
11 #
12 library(gdata) # suporte para leitura de planilhas
13 v - read.xls(xls='./data/Vazoes_Mensais_1931_2010.xls',sheet=1)
14 View(v)
15
16 ano - v[ANO] # primeira coluna
17 vaz - v[,-1] # todos os dados exceto a 1a coluna
18
19
20 # Aplica a função média nas colunas de v
21 vaz.m - apply(vaz,2,mean) # médias das vazões mensais
22 View(vaz.m)
79 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-94-320.jpg)
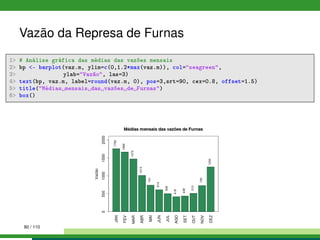


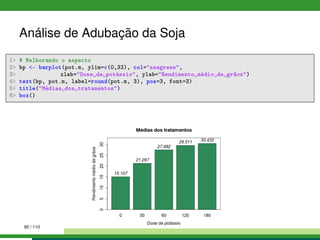
![Análise de Adubação da Soja
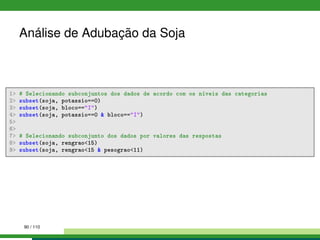
1 # Visualização rápida dos dados
2 head(soja) # cabeçalho
3 potassio agua bloco rengrao pesograo kgrao pgrao ts nvi nv
4 1 0 37.5 I 14.55 10.70 15.13 1.18 136 22 56
5 2 30 37.5 I 21.51 13.53 17.12 0.99 159 2 62
6 3 60 37.5 I 24.62 15.78 19.11 0.82 156 0 66
7 4 120 37.5 I 21.88 12.80 18.12 0.85 171 2 68
8 5 180 37.5 I 28.11 14.79 19.11 0.88 190 0 82
9 6 0 50.0 I 17.16 12.26 12.14 1.05 140 20 63
10
11 names(soja)
12 [1] potassio agua bloco rengrao pesograo kgrao pgrao ts
13 [9] nvi nv
85 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-101-320.jpg)
![Análise de Adubação da Soja
1 # Acessando informações das variáveis ($)
2
3 soja$bloco # a variável bloco foi lida como um fator (variável categórica)
4 [1] I I I I I I I I I I I I I I I II II II
5 [24] II II II II II II II III III III III III III III III III III III
6 [47] IV IV IV IV IV IV IV IV IV IV IV IV IV IV V V V V
7 [70] V V V V V V
8 Levels: I II III IV V
9
10 soja$rengrao
11 [1] 14.55 21.51 24.62 21.88 28.11 17.16 24.44 28.50 32.94 28.76 14.13 19.71
12 [16] 15.72 19.72 24.29 25.39 28.45 15.44 28.12 31.49 29.95 30.06 15.42 23.68
13 [31] 12.77 20.45 24.35 27.15 24.08 16.01 24.57 28.85 26.23 26.36 16.08 20.99
14 [46] 14.26 23.71 22.76 22.46 22.97 15.54 18.48 25.54 30.29 30.64 17.26 20.51
15 [61] 10.30 16.28 23.61 29.66 23.34 14.41 17.24 29.08 29.52 27.98 17.56 20.05
16
17 soja$potassio # a variável potassio também écategórica, mas foi lida como numérica
18 [1] 0 30 60 120 180 0 30 60 120 180 0 30 60 120 180 0 30 60
19 [24] 120 180 0 30 60 120 180 0 30 60 120 180 0 30 60 120 180 0
20 [47] 30 60 120 180 0 30 60 120 180 0 30 60 120 180 0 30 60 120
21 [70] 180 0 30 60 120 180
86 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-102-320.jpg)
![Análise de Adubação da Soja
1 # O comando attach() anexa a base de dados ao workspace do R
2 #
3 # Os objetos no banco de dados podem ser acessados simplesmente
4 # digitando seus nomes
5
6 attach(soja)
7 rengrao
8 [1] 14.55 21.51 24.62 21.88 28.11 17.16 24.44 28.50 32.94 28.76
9 ...
10 [73] 29.90 20.86 35.50
11
12 # Para desanexar a base de dados
13 detach(soja)
14 rengrao
15 Error: object 'rengrao' not found
87 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-103-320.jpg)
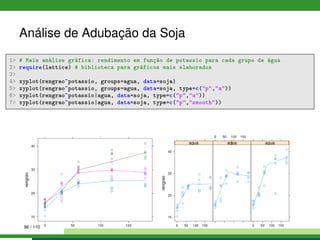
![Análise de Adubação da Soja
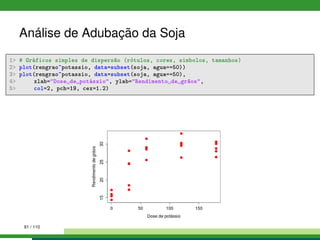
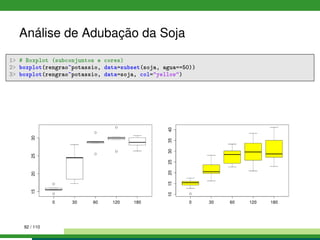
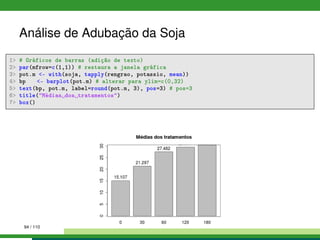
1 # Exploração númerica, médias por nível de potássio, água e potássio:água
2 attach(soja) # anexa a base de dados
3 levels(factor(potassio)) # factor() transforma a variável em categórica e levels() ←
extrai as categorias
4 [1] 0 30 60 120 180
5
6 tapply(rengrao,potassio,mean) # tapply() aplica um função a um grupo de valores de ←
um array
7 0 30 60 120 180
8 15.10733 21.29733 27.48200 29.51067 30.43200
9
10 tapply(rengrao,list(agua),mean)
11 37.5 50 62.5
12 21.6956 25.1040 27.4980
13
14 tapply(rengrao,list(potassio,agua),mean) # médias de rendimento para potassio:agua
15 37.5 50 62.5
16 0 13.520 15.712 16.090
17 30 20.334 22.570 20.988
18 60 23.926 28.692 29.828
19 120 25.308 29.786 33.438
20 180 25.390 28.760 37.146
88 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-104-320.jpg)

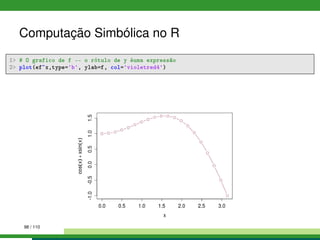
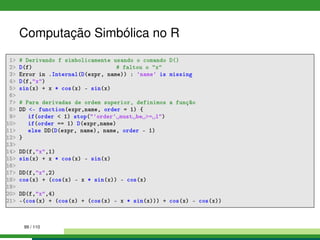
![Computação Simbólica no R
Em R podemos calcular as derivadas (simbólicas) de expressões
simples
1 # Operações simbólicas com expressões simples
2 rm(list=ls()) # limpa o espaço de trabalho
3
4 # Cria uma expressão simbólica
5 f = expression(cos(x) + x * sin(x))
6 class(f)
7 [1] expression
8
9 # Avalia a expressão, mas x ainda não exite...
10 eval(c)
11 Error in eval(expr, envir, enclos) : object 'x' not found
12
13 # Repetindo, mas agora com a criação de x
14 x=seq(0,pi,length=20)
15 eval(f)
16 [1] 1.00000000 1.01357652 1.05319340 1.11556315 1.19537338 1.28553021
17 [7] 1.37748586 1.46163791 1.52778475 1.56561949 1.56524303 1.51767600
18 [13] 1.41534884 1.25255020 1.02581462 0.73423276 0.37966969 -0.03311993
19 [19] -0.49648737 -1.00000000
97 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-114-320.jpg)
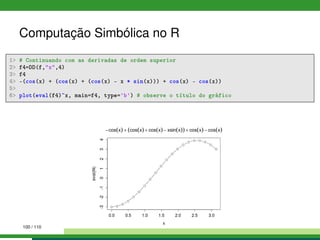


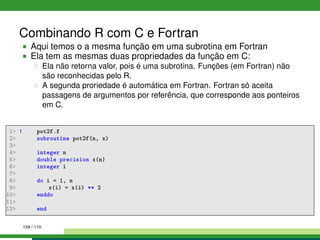
![Combinando R com C e Fortran
Aqui temos o código em linguagem C com uma solução para o
problema
O R exige duas proriedades da função:
A função não retorna nenhum valor. Todo o trabalho é feito mudando os
valores dos argumento.
Todos os argumentos são ponteiros. Em R, mesmo escalares são vetores
(de comprimento um).
1 /* pot2c.c */
2 void pot2c(int *nin, double *x)
3 {
4 int n = nin[0];
5 int i;
6
7 for (i=0; in; i++)
8 x[i] = x[i] * x[i];
9 }
103 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-122-320.jpg)

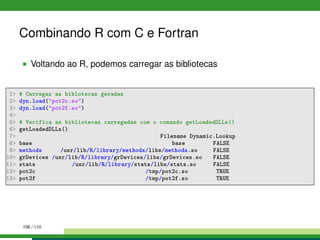
![Combinando R com C e Fortran
Executando o função em C
1 # Para testar, vamos criar um vetor x
2 x=c(1,2,3,4,5)
3 x
4 [1] 1 2 3 4 5
5
6 typeof(x) # x deve ser double, assim como o argumento na função em C
7 [1] double
8
9 # A chamada da função em R éfeita pelo comando .C()
10 .C(pot2c, n=length(x), x=x)
11 $n
12 [1] 5
13
14 $x
15 [1] 1 4 9 16 25
107 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-126-320.jpg)
![Combinando R com C e Fortran
Executando o subrotina em Fortran
1 # A chamada da subrotina em R éfeita pelo comando .Fortran()
2 .Fortran(pot2f, n=length(x), x=x)
3 $n
4 [1] 5
5
6 $x
7 [1] 1 4 9 16 25
108 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-127-320.jpg)
![Combinando R com C e Fortran
Uma solução mais agradável é criar uma função envelope
Permite checar alguns erros em R, o que é mais fácil que em C
Permite que alguns argumento calculados não sejam mostrados
Permite retornar somente o que o necessário
1 # Função envelope
2 pot2c - function(x) {
3 if (!is.numeric(x))
4 stop(O argumento x deve ser numérico)
5 out - .C(pot2c,
6 n=as.integer(length(x)),
7 x=as.double(x))
8 return(out$x)
9 }
10
11 # Executando a função
12 pot2c(x)
13 [1] 1 4 9 16 25
109 / 110](https://image.slidesharecdn.com/minir-121120115051-phpapp01/85/Mini-R-128-320.jpg)
