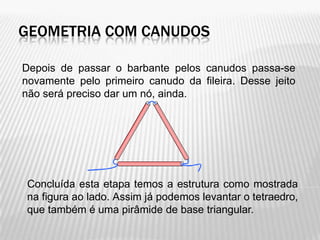
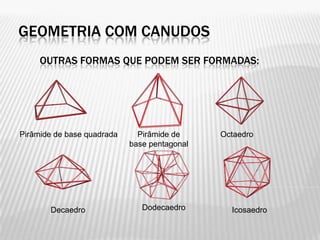
Este documento descreve como ensinar geometria espacial para crianças usando canudos de refrigerante. Ele explica como construir estruturas geométricas simples como um tetraedro e uma pirâmide de base quadrada usando canudos conectados por barbante. O documento também menciona outras formas geométricas que podem ser construídas dessa maneira.

1. GEOMETRIA COM CANUDOS
PROF. DEBORA VALIM SINAY NEVES

2. GEOMETRIA COM CANUDOS
A geometria é, freqüentemente, ensinada no quadro negro
ou através de livros didáticos. Quando se trata de figuras
planas esse método não representa grande dificuldade
para o aprendizado da criança.
Mas o mesmo não se pode dizer quando
se deseja ensinar os elementos da
geometria espacial. Portanto, neste
material, sugiro a utilização de canudos
de refrigerante na montagem de
estruturas geométricas, como a mostrada
na figura ao lado.

3. GEOMETRIA COM CANUDOS
Pode-se ensinar geometria espacial por intermédio da
montagem de sólidos, em que a criança recorta um
desenho numa folha de cartolina e, através de dobraduras
e colagem, monta um sólido geométrico.
Porém, a atividade que é
proposta aqui, além de
possibilitar que a criança
construa estruturas e
"brinque" com a
geometria espacial,
torna possível a visualização
de alguns elementos que na atividade com cartolina são
menos notados. Estes elementos são as arestas e os
vértices dos sólidos.

4. GEOMETRIA COM CANUDOS
A estrutura mais simples para se montar é a do tetraedro
(poliedro de quatro faces) que possui 6 arestas e 4
vértices. Na figura ao lado nota-se que cada aresta do
tetraedro corresponde a um canudo. Portanto, para
montá-lo será necessário dispor de 6 canudos de
refrigerante.

5. GEOMETRIA COM CANUDOS
Ligar um canudo ao outro pode parecer algo complicado
a princípio, mas essa tarefa ficará mais fácil depois de
algumas tentativas.
Para começar a construção da estrutura deve-se iniciar
pela base (alicerce), que é um triângulo. Se o tetraedro
é regular então o triângulo deverá ser equilátero. A
construção da base começa passando-se o barbante
por três canudos.

6. GEOMETRIA COM CANUDOS
Depois de passar o barbante pelos canudos passa-se
novamente pelo primeiro canudo da fileira. Desse jeito
não será preciso dar um nó, ainda.
Concluída esta etapa temos a estrutura como mostrada
na figura ao lado. Assim já podemos levantar o tetraedro,
que também é uma pirâmide de base triangular.

7. GEOMETRIA COM CANUDOS
Pegamos a ponta do barbante que acabamos de passar
pelo canudo da base e passamos por dois outros
canudos.

8. GEOMETRIA COM CANUDOS
Em seguida passamos o barbante por mais um canudo da
base. A ponta sairá na outra extremidade e poderemos
passá-la pelo último canudo.

9. GEOMETRIA COM CANUDOS
Assim como fizemos para fechar o triângulo da base,
faremos para fechar o tetraedro. Ou seja, passaremos
mais uma vez o barbante por dentro do canudo
mostrado na figura ao lado. Para que a estrutura fique
bem firme é interessante passar o barbante duas vezes
pelo mesmo canudo

10. GEOMETRIA COM CANUDOS
Com isso as extremidades adjacentes dos canudos
ficarão conectadas.Em vez de usar barbante para unir os
canudos pode-se usar bolinhas de isopor ou massa de
modelar.

11. GEOMETRIA COM CANUDOS
Outro poliedro que pode ser montado é o cubo
(hexaedro). Ele tem 6 faces e 12 arestas, necessitando,
assim, de 12 canudos. Porém a estrutura não ficará
estável, ou seja, ela não fica de pé facilmente. Sendo
preciso fazer várias conexões entre os vértices opostos.

12. GEOMETRIA COM CANUDOS
Já a pirâmide de base quadrada fica de pé, mas se
manuseada ela pode deformar-se. Para construí-la
serão necessários 8 canudos.

13. GEOMETRIA COM CANUDOS
OUTRAS FORMAS QUE PODEM SER FORMADAS:
Pirâmide de base quadrada Pirâmide de Octaedro
base pentagonal
Decaedro Dodecaedro Icosaedro

14. GEOMETRIA COM CANUDOS