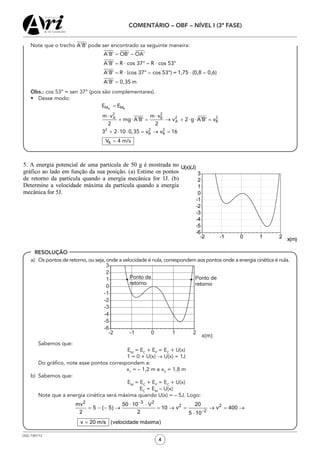
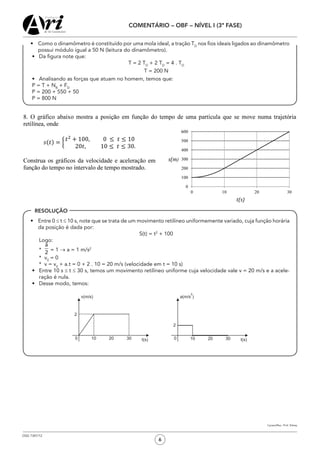
1) O documento apresenta resoluções de problemas de física relacionados a cinemática, dinâmica, termodinâmica e hidrostática. 2) As resoluções incluem análises de movimento retilíneo uniformemente variado, conservação da energia mecânica, dilatação térmica e empuxo em fluidos. 3) São mostrados cálculos para determinar aceleração, velocidade, variação de volume, forças envolvidas no movimento de um homem puxando uma prancha com cabos

1. COMENTÁRIO – OBF – NÍVEL I (3ª FASE)
Professor: Daniel Paixão, Edney Melo e Rômulo Mendes
ALUNO(A): Nº
TURMA: TURNO: DATA: _____/_____/______
COLÉGIO:
OSG 7347/12
Note que a escala apresentada corresponde o tempo de reação, em milisegundos (ms = 10– 3
s). Imaginando a
tira na vertical, temos que:
→ ponto que o colega segura a tira
| | = 10 m/s2
→ ponto onde você posiciona o polegar e o indicador0
y
Como se trata de um movimento de queda livre, temos que:
RESOLUÇÃO

2. OSG 7347/12
COMENTÁRIO – OBF – NÍVEL I (3ª FASE)
2
RESOLUÇÃO
RESOLUÇÃO
• Para um corpo totalmente submerso em um fluido qualquer, a força de empuxo será proporcional ao
volume do corpo considerado.
• Dess modo, temos que comparar qual dos dois corpos possui um volume maior.
Note que o cubo e a esfera possuem a mesma área superficial, logo, para um cubo de aresta a e uma
esfera de raio R, temos que:
• Determinemos agora o volume do cubo e o da esfera, para depois compará-los.
Note que a esfera possui um volume maior, de modo que o volume submerso é maior, logo ela está sujeita
a um maior empuxo.
Obs.: Aproximamos p = 3, para simplificação.
• Note que o problema afirma que os cilindros são feitos do mesmo material, ou seja, a densidade é a mesma
e o calor específico também é o mesmo para os três cilindros.
• Como as quantidades de calor transferidas para os três cilindros possuem o mesmo valor, temos que:
Q1
= Q2
= Q3
m1
. c . ∆T1
= m2
. c . ∆T2
= m3
. c . ∆T3
m1
. ∆T1
= m2
. ∆T2
= m3
. ∆T3
(d . V1
) . ∆T1
= (d . V2
) . ∆T2
= (d . V3
) . ∆T3
V1
. ∆T1
= V2
. ∆T2
= V2
. ∆T2

3. 3
COMENTÁRIO – OBF – NÍVEL I (3ª FASE)
OSG 7347/12
RESOLUÇÃO
• Note que os volumes iniciais, V1
, V2
e V3
, são relacionados da seguinte maneira.
• A variação do volume é diretamente proporcional ao volume e à variação de temperatura. Desse modo:
∆V = γ . Vi . ∆T
coeficiente de dilatação volumética
• Logo, temos que:
• Note que ∆V1
= ∆V2
= ∆V3
. Logo as variações de volume nos três cilindros são iguais.
Como não existe atrito no trecho citado, podemos resolver esse problema utilizando a conservação da energia
mecânica. Logo:
53°
37°
R
R
O
A
B
C
A’
B’
NHR (nível horizontal de referência)

4. OSG 7347/12
COMENTÁRIO – OBF – NÍVEL I (3ª FASE)
4
RESOLUÇÃO
Note que o trecho pode ser encontrado sa seguinte maneira:
Obs.: cos 53° = sen 37° (pois são complementares).
• Desse modo:
a) Os pontos de retorno, ou seja, onde a velocidade é nula, correspondem aos pontos onde a energia cinética é nula.
Sabemos que:
EM
= EC
+ EP
= EC
+ U(x)
1 = 0 + U(x) → U(x) = 1J
Do gráfico, note esse pontos correspondem a:
x1
= – 1,2 m e x2
= 1,8 m
b) Sabemos que:
EM
= EC
+ EP
= EC
+ U(x)
EC
= EM
– U(x)
Note que a energia cinética será máxima quando U(x) = – 5J. Logo:

5. 5
COMENTÁRIO – OBF – NÍVEL I (3ª FASE)
OSG 7347/12
RESOLUÇÃO
RESOLUÇÃO
• Note que o cabo ideal que passa pelas roldanas é o mesmo, de modo, que o módulo da força de tração
é a mesma em todos os pontos, inclusive na mão do homem (a força de 200 N, citada no problema).
• Considerando o homem e a prancha como um único sistema, podemos identificar as seguintes forças e/
ou componentes:
• Da segunda Lei de Newton, temos que:
3.T – p . sen 30° = M.a
3 . 200 – 1200 . 0,5 = M.a
M.a = 0
a = 0
• A aceleração do conjunto é nula, de modo que o sistema se move com velocidade constante.
• Do enunciado do problema, podemos fazer o seguinte diagrama de forças.

6. OSG 7347/12
COMENTÁRIO – OBF – NÍVEL I (3ª FASE)
6
RESOLUÇÃO
• Como o dinamômetro é constituído por uma mola ideal, a tração TD
nos fios ideais ligados ao dinamômetro
possui módulo igual a 50 N (leitura do dinamômetro).
• Da figura note que:
T = 2 TD
+ 2 TD
= 4 . TD
T = 200 N
• Analisando as forças que atuam no homem, temos que:
P = T + NB
+ FD
P = 200 + 550 + 50
P = 800 N
• Entre 0 ≤ t ≤ 10 s, note que se trata de um movimento retilíneo uniformemente variado, cuja função horária
da posição é dada por:
S(t) = t2
+ 100
Logo:
* = 1 → a = 1 m/s2
* v0
= 0
* v = v0
+ a.t = 0 + 2 . 10 = 20 m/s (velocidade em t = 10 s)
• Entre 10 s ≤ t ≤ 30 s, temos um movimento retilíneo uniforme cuja velocidade vale v = 20 m/s e a acele-
ração é nula.
• Desse modo, temos:
Cynara/Rev.: Prof. Edney