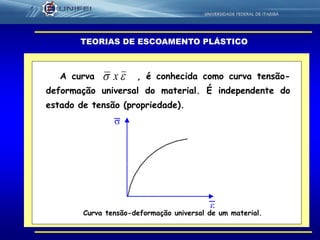
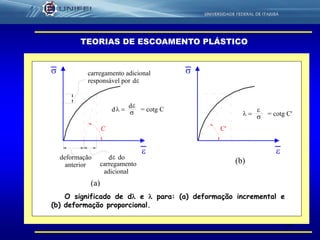
O documento discute teorias de escoamento plástico e critérios de resistência. Apresenta o critério de Von Mises, que propõe que o escoamento ocorre quando a energia de distorção atinge um valor crítico, e o critério de Tresca, que propõe que o escoamento ocorre quando a tensão de cisalhamento máxima atinge o valor da tensão de cisalhamento no escoamento sob tração uniaxial. Explica como esses critérios podem ser expressos matematicamente e comparados.