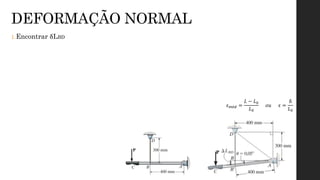
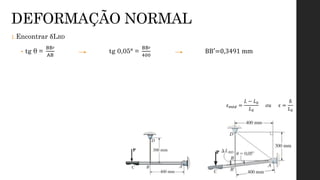
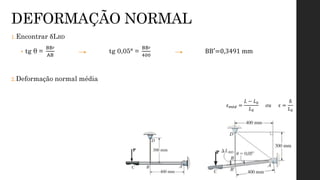
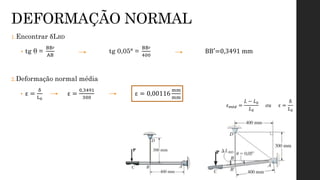
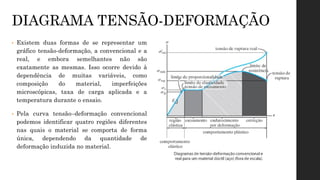
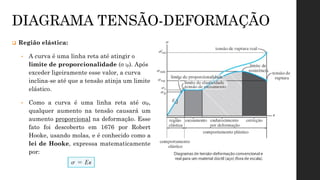
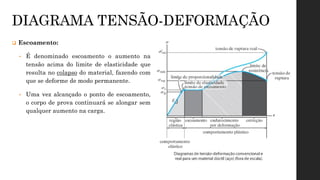
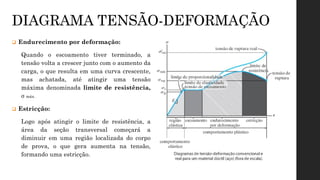
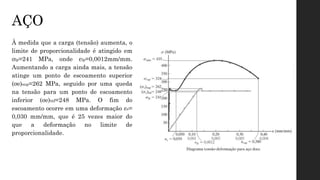
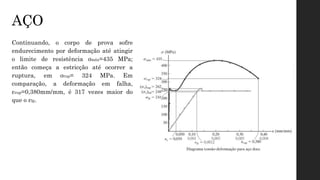
O documento aborda os conceitos de deformação em materiais, explicando como forças aplicadas resultam em mudanças na forma e tamanho dos corpos, com ênfase em deformação normal e por cisalhamento. É discutida a relação entre tensão e deformação através de ensaios mecânicos, como tração e compressão, que geram o diagrama tensão-deformação, crucial para entender o comportamento de diferentes materiais. Além disso, são apresentadas as fases do comportamento dos materiais sob tensão, incluindo elasticidade, escoamento, endurecimento por deformação e estricção.

1. Resistência dos Materiais I
Engenharia Civil – 5º período
Prof.ª Stella Ramos
Aula 3 – Deformação

2. CONCEITOS INICIAIS
• Sempre que uma força é aplicada a um corpo, esta tende a mudar a forma e o tamanho dele. Essas
mudanças são denominadas deformações e podem ser altamente visíveis ou praticamente
imperceptíveis se não forem utilizados equipamentos que façam medições precisas.
• Vale lembrar que qualquer tensão produz uma deformação equivalente nos materiais, que depende
tanto das características geométricas quanto do tipo material que são formados.
• Na engenharia, a deformação de um corpo é especificada pelo conceito de deformação normal e por
cisalhamento. Nesse tópico serão definidas essas quantidades e mostrado como elas podem ser
determinadas para vários tipos de problemas.

3. CONCEITOS INICIAIS

4. • O alongamento ou contração de um segmento de reta por unidade de comprimento é
denominado deformação normal.
• Se uma carga axial P for aplicada na barra da figura a seguir, o comprimento da barra mudará
de L0 para L. Define-se, portanto, como deformação normal média da barra, ε (épsilon), a
mudança em seu comprimento, δ (delta) = L – L0, divido pelo seu comprimento original, isto é:
ε𝑚é𝑑 =
𝐿 − 𝐿0
𝐿0
𝑜𝑢 ε =
δ
𝐿0
DEFORMAÇÃO NORMAL

5. • ε é uma mudança de comprimento por unidade de comprimento, e é positivo quando o
comprimento inicial se alonga, e negativo quando o comprimento se contrai.
• A deformação normal é uma quantidade adimensional, visto que é uma razão entre dois
comprimentos. Contudo, às vezes é comum expressá-la em termos de uma razão entre unidades
de comprimento (μm/m). Por serem medidas muito pequenas, uma representação comum é:
• μm, onde 1 μm = 10−6m
• Exemplo: 10 μm/m, ou ainda 10 μ
DEFORMAÇÃO NORMAL

6. • Exemplo: Quando uma força P é aplicada no braço rígido ABC da alavanca, o braço gira no
sentido anti-horário em torno do pino A, num ângulo de 0,05°. Determine a deformação normal
no cabo BD.
DEFORMAÇÃO NORMAL
ε𝑚é𝑑 =
𝐿 − 𝐿0
𝐿0
𝑜𝑢 ε =
δ
𝐿0

7. 1.Encontrar δLBD
DEFORMAÇÃO NORMAL
ε𝑚é𝑑 =
𝐿 − 𝐿0
𝐿0
𝑜𝑢 ε =
δ
𝐿0

8. 1.Encontrar δLBD
• tg θ =
BB′
AB
tg 0,05° =
BB′
400
BB′=0,3491 mm
DEFORMAÇÃO NORMAL
ε𝑚é𝑑 =
𝐿 − 𝐿0
𝐿0
𝑜𝑢 ε =
δ
𝐿0

9. 1.Encontrar δLBD
• tg θ =
BB′
AB
tg 0,05° =
BB′
400
BB′=0,3491 mm
2.Deformação normal média
DEFORMAÇÃO NORMAL
ε𝑚é𝑑 =
𝐿 − 𝐿0
𝐿0
𝑜𝑢 ε =
δ
𝐿0

10. 1.Encontrar δLBD
• tg θ =
BB′
AB
tg 0,05° =
BB′
400
BB′=0,3491 mm
2.Deformação normal média
• ε =
δ
L0
ε =
0,3491
300
ε = 0,00116
mm
mm
DEFORMAÇÃO NORMAL
ε𝑚é𝑑 =
𝐿 − 𝐿0
𝐿0
𝑜𝑢 ε =
δ
𝐿0

11. • As deformações não só fazem que os segmentos de reta se alonguem ou contraiam, mas também
que mudem de direção. Se selecionarmos dois segmentos de reta que estão originalmente
perpendiculares um ao outro, a mudança de ângulo que ocorre entre eles é referida como
deformação por cisalhamento.
• Esse ângulo é denotado por γ (gama) e é sempre medido em radianos (rad), que são
adimensionais.
DEFORMAÇÃO POR CISALHAMENTO

12. • Dessa forma, a deformação por cisalhamento pode ser representada por:
γ =
π
2
− θ
• Observe que, se θ for menor que
π
2
, a deformação por cisalhamento é positiva, ao passo que se θ
for maior que
π
2
, então a deformação por cisalhamento é negativa.
DEFORMAÇÃO POR CISALHAMENTO

13. • Exemplo: A chapa retangular está sujeita à deformação mostrada pela linha tracejada.
Determine a deformação por cisalhamento média γxy na chapa.
DEFORMAÇÃO POR CISALHAMENTO

14. 1. Encontrar θ
DEFORMAÇÃO POR CISALHAMENTO
γ =
π
2
− θ

15. 1. Encontrar θ
• 𝜃 =
π
2
+ θ′
DEFORMAÇÃO POR CISALHAMENTO
γ =
π
2
− θ

16. 1. Encontrar θ
• 𝜃 =
π
2
+ θ′
 𝑡𝑔 𝜃′ =
3
150
𝜃′
= 0,02 𝑟𝑎𝑑
• 𝜃 =
π
2
+ 0,02
DEFORMAÇÃO POR CISALHAMENTO
γ =
π
2
− θ

17. 1. Encontrar θ
• 𝜃 =
π
2
+ θ′
 𝑡𝑔 𝜃′ =
3
150
𝜃′
= 0,02 𝑟𝑎𝑑
• 𝜃 =
π
2
+ 0,02
2. Deformação por cisalhamento
• γ =
π
2
− θ
DEFORMAÇÃO POR CISALHAMENTO
γ =
π
2
− θ

18. 1. Encontrar θ
• 𝜃 =
π
2
+ θ′
 𝑡𝑔 𝜃′ =
3
150
𝜃′
= 0,02 𝑟𝑎𝑑
• 𝜃 =
π
2
+ 0,02
2. Deformação por cisalhamento
• γ =
π
2
− θ γ =
π
2
−
π
2
+ 0,02 γ = −0,02 𝑟𝑎𝑑
DEFORMAÇÃO POR CISALHAMENTO
γ =
π
2
− θ

19. Resistência dos Materiais I
Engenharia Civil – 5º período
Prof.ª Stella Ramos
Propriedades mecânicas dos materiais

20. INTRODUÇÃO
• Tendo discutido os conceitos básicos de tensão e deformação, o objetivo desse tópico é mostrar
como a tensão pode ser relacionada à deformação por meio de métodos experimentais para
determinar o diagrama tensão-deformação para um material específico.

21. ENSAIO DE TRAÇÃO E COMPRESSÃO
• A resistência de um material depende de sua capacidade de suportar uma carga sem
deformação excessiva ou falha. Esta propriedade é inerente ao próprio material e um dos testes
mais importantes para esses casos é o ensaio de tração ou compressão.

22. • Uma vez conhecidos os dados de tensão e deformação a partir do ensaio, é possível produzir
uma curva chamada diagrama tensão-deformação, que relaciona a tensão e a deformação
normal média em muitos materiais usados na engenharia, como metais, cerâmicas, polímeros e
compósitos.
• Lembrando que:
DIAGRAMA TENSÃO-DEFORMAÇÃO

23. • Existem duas formas de se representar um
gráfico tensão-deformação, a convencional e a
real, e embora semelhantes não são
exatamente as mesmas. Isso ocorre devido à
dependência de muitas variáveis, como
composição do material, imperfeições
microscópicas, taxa de carga aplicada e a
temperatura durante o ensaio.
• Pela curva tensão–deformação convencional
podemos identificar quatro regiões diferentes
nas quais o material se comporta de forma
única, dependendo da quantidade de
deformação induzida no material.
DIAGRAMA TENSÃO-DEFORMAÇÃO

24.  Região elástica:
• A curva é uma linha reta até atingir o
limite de proporcionalidade (σ lp). Após
exceder ligeiramente esse valor, a curva
inclina-se até que a tensão atinja um limite
elástico.
• Como a curva é uma linha reta até σlp,
qualquer aumento na tensão causará um
aumento proporcional na deformação. Esse
fato foi descoberto em 1676 por Robert
Hooke, usando molas, e é conhecido como a
lei de Hooke, expressa matematicamente
por:
DIAGRAMA TENSÃO-DEFORMAÇÃO

25. • Aqui, E representa a constante de proporcionalidade, chamada módulo de elasticidade ou
módulo de Young.
• Este, descreve a inclinação da porção de linha reta do diagrama. Uma vez que a deformação é
adimensional, E terá as mesmas unidades que a tensão, como pascal (Pa), megapascal (MPa)
ou gigapascal (GPa).
DIAGRAMA TENSÃO-DEFORMAÇÃO

26.  Escoamento:
• É denominado escoamento o aumento na
tensão acima do limite de elasticidade que
resulta no colapso do material, fazendo com
que se deforme de modo permanente.
• Uma vez alcançado o ponto de escoamento,
o corpo de prova continuará se alongar sem
qualquer aumento na carga.
DIAGRAMA TENSÃO-DEFORMAÇÃO

27.  Endurecimento por deformação:
Quando o escoamento tiver terminado, a
tensão volta a crescer junto com o aumento da
carga, o que resulta em uma curva crescente,
mas achatada, até atingir uma tensão
máxima denominada limite de resistência,
σ máx.
 Estricção:
Logo após atingir o limite de resistência, a
área da seção transversal começará a
diminuir em uma região localizada do corpo
de prova, o que gera aumenta na tensão,
formando uma estricção.
DIAGRAMA TENSÃO-DEFORMAÇÃO

28. DIAGRAMA TENSÃO-DEFORMAÇÃO

29. À medida que a carga (tensão) aumenta, o
limite de proporcionalidade é atingido em
σlp=241 MPa, onde εlp=0,0012mm/mm.
Aumentando a carga ainda mais, a tensão
atinge um ponto de escoamento superior
(σe)sup=262 MPa, seguido por uma queda
na tensão para um ponto de escoamento
inferior (σe)inf=248 MPa. O fim do
escoamento ocorre em uma deformação εe=
0,030 mm/mm, que é 25 vezes maior do
que a deformação no limite de
proporcionalidade.
AÇO

30. Continuando, o corpo de prova sofre
endurecimento por deformação até atingir
o limite de resistência σmáx=435 MPa;
então começa a estricção até ocorrer a
ruptura, em σrup= 324 MPa. Em
comparação, a deformação em falha,
εrup=0,380mm/mm, é 317 vezes maior do
que o εlp.
AÇO