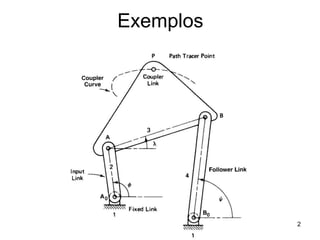
O documento apresenta uma análise de mecanismos de quatro barras, incluindo uma análise geral do mecanismo, exemplos de aplicações, e uma análise de pontos de interesse. Apresenta equações cinemáticas, critérios de Grashof para classificar os mecanismos, e cálculos de posição, velocidade e aceleração de pontos selecionados.