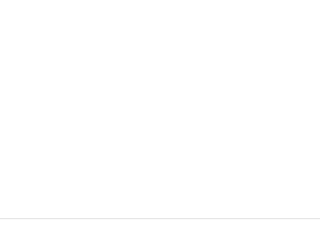
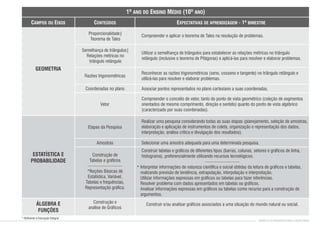
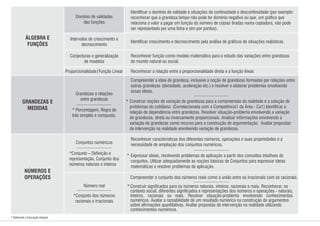
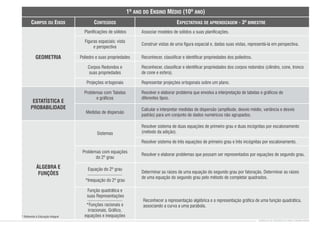
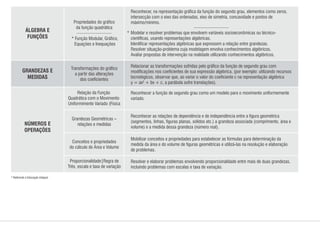
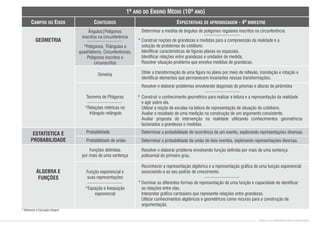
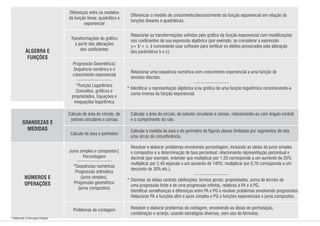
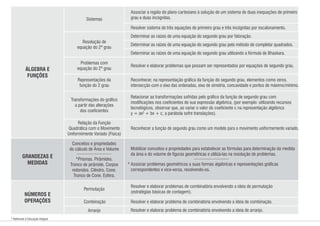
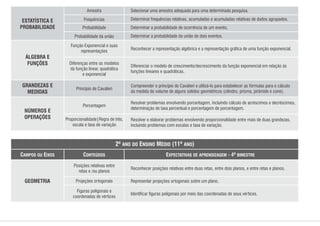
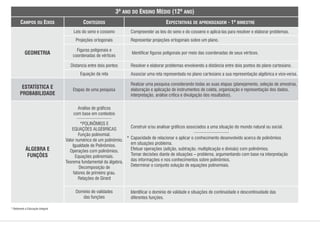
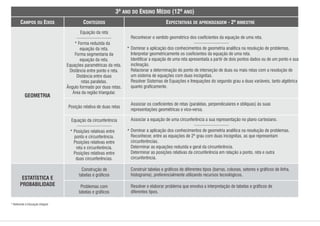
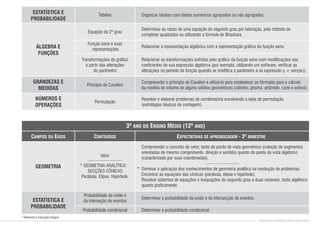
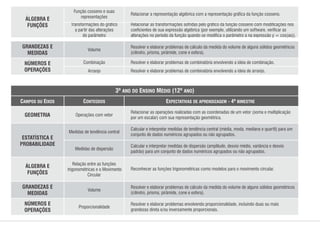
1) O documento apresenta os conteúdos de matemática para cada bimestre do ensino médio no estado de Pernambuco, de acordo com os parâmetros curriculares estaduais.
2) Os conteúdos são organizados em eixos como álgebra, geometria, estatística e probabilidade.
3) Para cada bimestre são listados os principais tópicos a serem abordados dentro de cada eixo temático.