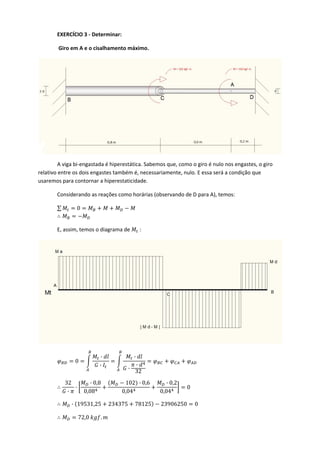
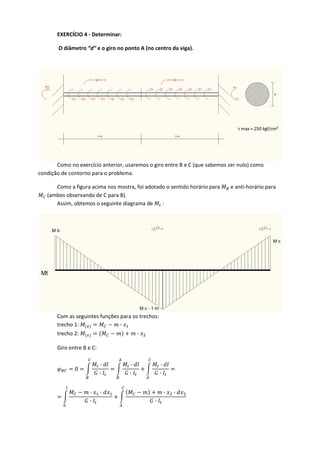
1) Os exercícios propõem problemas de torção em vigas e discos para determinar tensões, cisalhamentos e giros. 2) As condições de contorno utilizadas relacionam deformações e giros nos pontos de engaste. 3) Os diagramas de momento torção permitem calcular tensões, cisalhamentos e giros nos diferentes trechos.

1. UNIVERSIDADE ESTADUAL DE CAMPINAS
FACULDADE DE ENGENHARIA CIVIL
Departamento de Estruturas
EXERCÍCIOS DE TORÇÃO
RESISTÊNCIA DOS MATERIAIS II
Prof. Dr. Nilson Tadeu Mascia
Bolsista PAD: Renato Saldanha Victor
Campinas,Novembro ‐ 2009

2.
EXERCÍCIO 1 ‐ Determinar:
Tensão nos tirantes, cisalhamento máximo e o giro da extremidade livre (giro entre B e A).
O binário, causado pelas reações das forças de tração nos tirantes, gera um momento torçor
T no disco: 2 · 0,08 · ; onde N é a força normal existente em cada
tirante.
Isso nos leva a uma situação hiperestática. Além do engaste, temos a reação do momento T.
A condição de contorno que usaremos será a relação da deformação dos tirantes com o giro
no ponto C (medido a partir do ponto B, um engaste, que terá variação nula do giro em relação à sua
posição original), conforme a figura:
Assim, temos:
∆

3. Pela Lei de Hooke: ∆
·
·
· ,
· ·
·
Giro:
·
·
Seção circular cheia:
· · ,
1,571 10
O exercício nos leva ao seguinte diagrama de momento torçor:
Com o primeiro trecho determinado pela seguinte função: 12 0,08 · .
E o segundo trecho com a função: 12 .
Assim, temos:
·
·
12 0,08 · · 0,8
· 1,571 · 10
611,5 4,074 · ·
10
Ou seja:
611,5 4,074 · ·
10
2
·
10
·
1
0,04
611,5 4,074 · · 8 ·
Considerando:
2,1 · 10 ; 8 · 10 21
Assim:
611,5 4,074 · · 8 · 2,625
12841,5 85,554 1 ·
148,364
Tensão nos tirantes:
148,364
4
,

4.
Cisalhamento máximo: (seção circular cheia)
á á · 16
· ³
Substituindo, nas funções do diagrama de , o valor de encontrado acima, temos:
Assim, temos o momento torçor máximo em todo o trecho 12 . .
1200 · 16
· 2
,
Giro entre B e A:
·
·
12 0,08 · 148,364 · 0,8
· 1,571 · 10
12 · 0,2
· 1,571 · 10
1,019 · 10 1,910 · 10
, , °

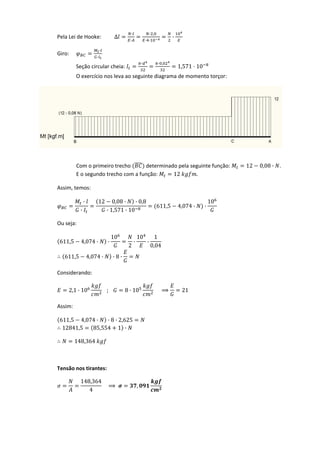
5. EXERCÍCIO 2 ‐ Determinar:
Tensão nos tirantes, cisalhamento máximo
Como no exercício anterior, temos uma situação hiperestática que será contornada
relacionando o giro no ponto B com a deformação dos tirantes.
Assim, temos:
∆
Lei de Hooke:
∆
·
·
· 200
· · 1²
63,662 ·
Giro:
·
·
Seção circular cheia:
· ·
9,817 10
Diagrama de momento torçor:
Funções dos trechos:
: 10 · 70000 [kgf.cm]
: 10 · [kgf.cm]

6. Assim, temos:
·
·
10 · 70000 · 100
· 9,817 · 10
10 · · 100
· 9,817 · 10
0,1019 · 20 · 70000 2,0372 · 3500
Portanto:
∆ 2,0372 · 3500 63,662 ·
·
1
5
2,0372 · 5 · 3500
63,662
·
0,16 · 3500
Como o exercício nos diz que 0,4 · , temos:
0,4 · ·
0,16 · 3500 1,4 · 1400
OBS: O sinal negativo para o momento torçor, no cálculo do giro, existe apenas para que o
giro encontrado seja no sentido anti‐horário (observando de C para A). Sentido da solicitação
(momento de 700kgf.m) e sentido concordante com o das deformações dos tirantes.
Tensão normal nos tirantes:
1000
· 1²
,
Cisalhamento máximo: (seção circular cheia)
á á · 16
· ³
Substituindo, nas funções do diagrama de , o valor de encontrado acima, temos:
Assim, temos o momento torçor máximo em todo o trecho 60000 . .
60000 · 16
· 10
,

7. EXERCÍCIO 3 ‐ Determinar:
Giro em A e o cisalhamento máximo.
A viga bi‐engastada é hiperestática. Sabemos que, como o giro é nulo nos engastes, o giro
relativo entre os dois engastes também é, necessariamente, nulo. E essa será a condição que
usaremos para contornar a hiperestaticidade.
Considerando as reações como horárias (observando de D para A), temos:
∑ 0
E, assim, temos o diagrama de :
0
·
·
·
·
·
32
32
·
·
· 0,8
0,08
102 · 0,6
0,04
· 0,2
0,04
0
· 19531,25 234375 78125 23906250 0
72,0 .

8. Giro em A:
Para encontrar o giro em A, temos que relacioná‐lo com algum ponto fixo (um dos engastes).
No caso, é mais simples calcular o giro entre A e D.
·
·
72 · 10 · 20
8 · 10 ·
· 4
32
, ·
ou , °
Cisalhamento máximo:
Como não temos uma seção constante, precisamos comparar os valores obtidos para
determinar o máximo.
Assim:
72
· 0,08 /16
;
30
· 0,04 /16
;
72
· 0,04 /16
, /
A comparação poderia também ter sido feita da seguinte forma:
Temos três trechos de seção constante e com valores de diferentes. Porém, os dois
últimos ( e ) têm a mesma seção e, assim, podemos apenas comparar o valor de para esses
dois casos. O que nos descarta a possibilidade de que o 2º trecho seja o máximo.
Como os dois trechos remanescentes possuem o mesmo valor de , podemos comparar o
valor de que, por sua vez, é determinado pelo diâmetro (já que as duas seções em questão são do
mesmo tipo ‐ circular cheia). Assim, temos que o cisalhamento máximo ocorre no trecho 3, que tem
diâmetro menor.

9. EXERCÍCIO 4 ‐ Determinar:
O diâmetro “d” e o giro no ponto A (no centro da viga).
Como no exercício anterior, usaremos o giro entre B e C (que sabemos ser nulo) como
condição de contorno para o problema.
Como a figura acima nos mostra, foi adotado o sentido horário para e anti‐horário para
(ambos observando de C para B).
Assim, obtemos o seguinte diagrama de :
Com as seguintes funções para os trechos:
trecho 1: ·
trecho 2: ·
Giro entre B e C:
0
·
·
·
·
·
·
· ·
·
· ·
·

10. · 1
· 1
2
· 1
· 1
2
·
1
·
0
2 ·
2 ·
2
0
2
1 .
Cisalhamento máximo:
Ocorre no ponto B, C ou A. Porém, todos possuem | | 1 . .
á 1 · 16
· ³
250 · 10 / ²
16
· 250 · 10
, ; ,
Giro em A:
·
·
· ·
·
1 2 · ·
·
1 · 1 2 ·
1
2
·