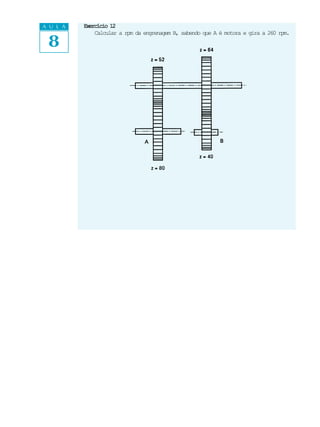
Este documento fornece instruções sobre como calcular RPM (rotações por minuto) usando relações entre diâmetros de polias ou número de dentes de engrenagens. Explica que a RPM transmitida depende da relação entre os componentes do conjunto transmissor e fornece fórmulas matemáticas para calcular RPM.