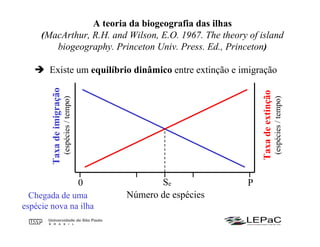
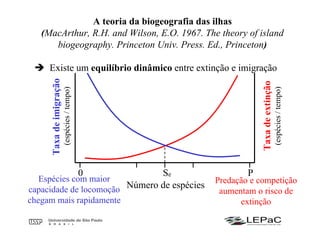
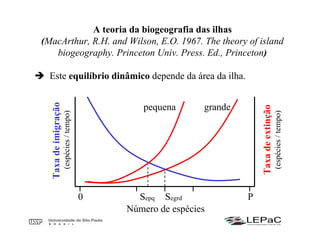
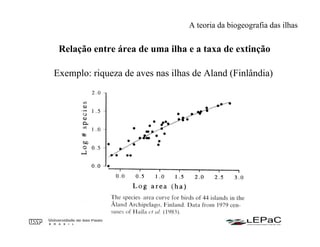
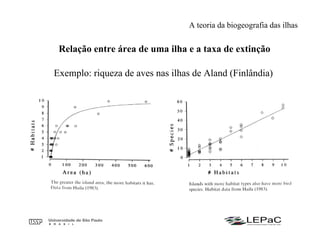
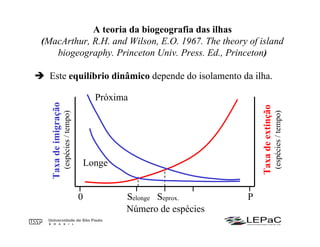
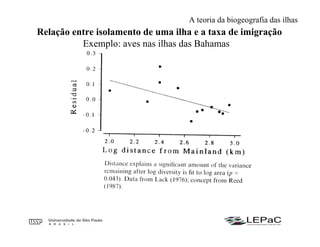
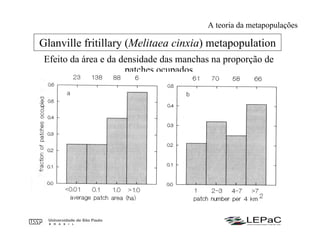
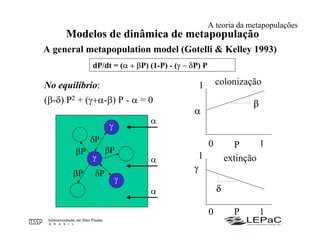
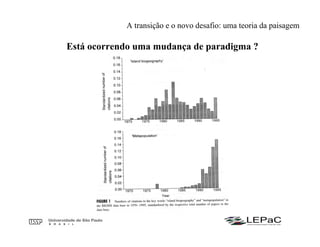
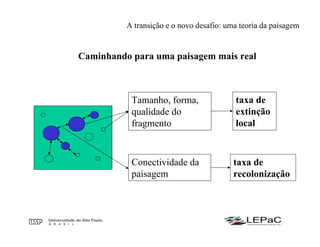
O documento discute as teorias da biogeografia de ilhas e de metapopulações. A teoria da biogeografia de ilhas propõe que a riqueza de espécies em uma ilha depende de um equilíbrio dinâmico entre taxas de extinção e imigração, influenciadas pelo tamanho e isolamento da ilha. A teoria de metapopulações descreve populações fragmentadas como conjuntos de subpopulações locais unidas por fluxos de migração, sujeitas a extinções e recolonizações locais. O modelo