Baixado 11 vezes
Carregado porAdilmar Dantas
Potenciação Divide and Conquer
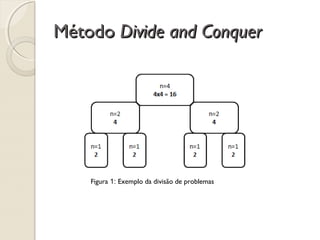
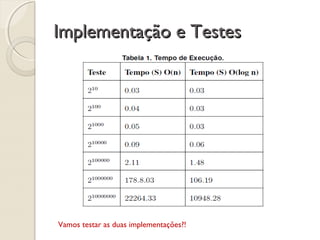
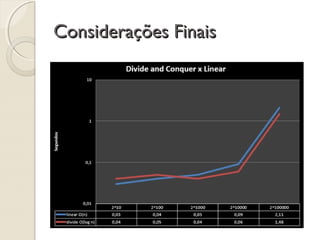
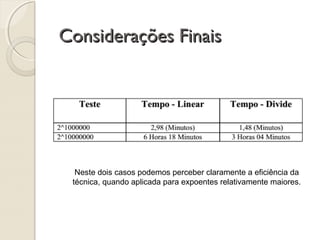
O documento descreve o método "divide and conquer" para resolver o problema da potenciação. Ele divide o problema em subproblemas menores, resolve os subproblemas de forma recursiva e combina as soluções para obter a solução final. O método é mais eficiente do que o método iterativo para grandes valores de entrada, pois reduz o tempo de execução de forma exponencial conforme o tamanho do problema aumenta.
Potenciação Divide and Conquer
- 1. MétodoMétodo Divide andConquerDivide and Conquer para opara o problema de Potênciaproblema de Potência Alunos: Adilmar Coelho Dantas Sara Luzia de Melo PÓS-GRADUAÇÃO EM CIÊNCIA DA COMPUTAÇÃO Universidade Federal de Uberlândia – UFU Faculdade de Computação – FACOM
- 2. IntroduçãoIntrodução Problema - Dado umnúmero inteiro n e um inteiro x não negativo, desenvolver um algoritmo que retorne o valor da potência. Solução Proposta Método Iterativo Método Recursivo Método Divide and Conquer Função pow
- 3. Método IterativoMétodo Iterativo Tempo de Execução: Custo Linear!!!
- 4. MétodoMétodo Divide andConquerDivide and Conquer Figura 1: Exemplo da divisão de problemas
- 5. MétodoMétodo Divide andConquerDivide and Conquer 5 multiplicações
- 6. MétodoMétodo Divide andConquerDivide and Conquer
- 7.
- 8. Se par Se ímpar Custodo algoritmo: Tempo do algoritmoTempo do algoritmo divide and conquerdivide and conquer
- 9. Implementação e TestesImplementaçãoe Testes Vamos testar as duas implementações?!
- 10. Foi observado queo tempo do algoritmo divide and conquer foi superior ao tempo do algoritmo iterativo para com n relativamente pequeno. - Isto ocorre ao fato de nem todos os subproblemas gerados serem utilizados na operação. Quando o valor de entrada “cresce”, o tempo de execução do algoritmo divide and conquer diminui comparado ao linear. Concluimos que, o método divide and conquer para esse problema de potência é eficiente quando os valores de entrada são “grandes”. Considerações FinaisConsiderações Finais
- 11.
- 12. Considerações FinaisConsiderações Finais Nestedois casos podemos perceber claramente a eficiência da técnica, quando aplicada para expoentes relativamente maiores.
- 13. ReferênciasReferências • Cormen, T.H., Leiserson, C. E., Rivest, R. L., and Stein, C. (2002). Algoritmos, Teoria e Prática (2. ed.). MIT Press.