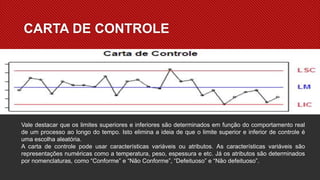
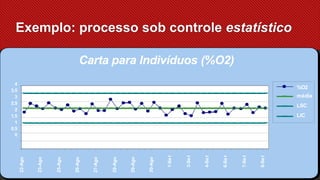
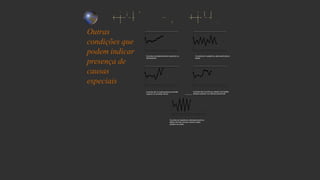
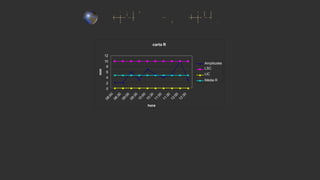
O documento descreve as sete ferramentas da qualidade, com foco na carta de controle. A carta de controle é uma ferramenta gráfica que auxilia no monitoramento de processos e variações através de limites estatísticos de controle. Ela pode identificar causas especiais de variação que levam o processo para fora de controle estatístico.

1. FERRAMENTAS DA
QUALIDADE
INSTRUTORA: MILENY DE LIMA SANTOS
mileny.santos@ms.senai.br - 67 99236.2675

2. OBJETIVO
Conhecer e utilizar ferramentas de qualidade para chegar a
um grau de eficiência/eficácia em uma determinada atividade
ou processo.

3. SETE FERRAMENTAS DA QUALIDADE

4. O que é Carta de Controle?
A Carta de Controle é uma ferramenta gráfica que pode auxiliar
visualmente no acompanhamento dos processos e suas possíveis
variabilidades. A carta de controle, também conhecido como gráfico de
controle, é uma ótima opção para identificar estatisticamente os desvios
ou alterações não esperadas que podem ocorrer em determinada etapa
de um processo.
A principal forma de elaborar um gráfico de controle é utilizando como
base o desvio padrão de um determinado processo.
CARTA DE CONTROLE

5. Visualmente o gráfico de controle possui:
Linha superior de controle – é uma linha constante no gráfico que indica os limites
máximos de controle em determinado processo (limite superior de controle = 3 vezes
maior ao desvio padrão)
Linha inferior de controle – é uma linha constante no gráfico que indica os limites
inferiores de controle em determinado processo (limite inferior de controle = 3 vezes
menores ao desvio padrão)
Linha central – esta representa a variação ao longo de um período de tempo,
podendo ser localizada acima da linha superior, abaixo da linha inferior de controle ou
entre ambas. Quando localizado entre o limite superior e o inferior demonstra que
existe um desvio padrão menor do que as variações permitidas.
CARTA DE CONTROLE

6. Vale destacar que os limites superiores e inferiores são determinados em função do comportamento real
de um processo ao longo do tempo. Isto elimina a ideia de que o limite superior e inferior de controle é
uma escolha aleatória.
A carta de controle pode usar características variáveis ou atributos. As características variáveis são
representações numéricas como a temperatura, peso, espessura e etc. Já os atributos são determinados
por nomenclaturas, como “Conforme” e “Não Conforme”, “Defeituoso” e “Não defeituoso”.
CARTA DE CONTROLE

7. Cartas de controle- CEP
APLICAÇÃO: quando se necessitar verificar quanto de
variabilidade do processo é devido à variação e quanto é
devido a causas comuns/ ações individuais, a fim de se
determinar se o processo está sob controle estatístico.

8. Cartas de
controle- CEP
A CARTA
simplesmente
DE
um
CONTROLE é
gráfico de
acompanhamento com uma linha
superior (LSC) e uma linha inferior (LIC)
média do
em cada lado da linha
processo, todos estatisticamente
determinados.

9. Exemplo: processo sob controle estatístico
Carta para Indivíduos (%O2)
4
3,5
3
2,5
2
1,5
1
0,5
0
22-Ago
23-Ago
25-Ago
26-Ago
27-Ago
29-Ago
29-Ago
30-Ago
1-Se
t
3-Se
t
4-Se
t
6-Se
t
7-Se
t
9-Se
t
%O2
média
LSC
LIC

10. Exemplo: um processo pode
ser consistentemente ruim
Carta para Indivíduos (%O2)
4
3,5
3
2,5
2
1,5
1
0,5
0
22-Ago
23-Ago
25-Ago
26-Ago
27-Ago
29-Ago
29-Ago
30-Ago
1-Set
3-Set
4-Set
6-Set
7-Set
9-Set
%O2
média
LSC
LIC
LSE
LIE

11. Existem dois tipos de carta
de controle:
1. Por variáveis - grandezas
quantificáveis: m, massa, resistência à
compressão, mm, etc.
2. De atributo – peça aprovada ou
reprovada.

12. Cartas de controle
por variáveis:
➢ Passos:
➢ Cartas e R
➢ Determinação da média ( ) e da
amplitude (R)
Onde: n= número de
amostras (observações)
em cada subgrupo
R = X máx – X mín

13. Cartas de controle
por variáveis:
➢ Determinação da média do processo ( )
e a média da amplitude ( )
Onde:
K= número de
subgrupos

14. Cartas de controle
por variáveis:
➢ Calcula-se os limites de controle

15. n c4 d2 d3 A2 A3 B3 B4 D3 D4
2 0.798 1.128 0.853 1.880 2.659 0 3.267 0 3.267
3 0.886 1.693 0.888 1.023 1.954 0 2.568 0 2.575
4 0.921 2.059 0.88 0.729 1.628 0 2.266 0 2.282
5 0.940 2.326 0.864 0.577 1.427 0 2.089 0 2.115
6 0.952 2.534 0.848 0.483 1.287 0.030 1.970 0 2.004
10 0.973 3.078 0.797 0.308 0.975 0.248 1.716 0.223 1.777
15 0.982 3.472 0.756 0.223 0.789 0.428 1.572 0.347 1.653
20 0.987 3.735 0.729 0.180 0.680 0.510 1.490 0.415 1.585
25 0.990 3.931 0.708 0.153 0.606 0.565 1.435 0.459 1.541
Fatores de correção
para cartas e
R

16. INTERPRETANDO
CARTAS DE CONTROLE

17. Porque se faz
“Carta de
Controle”?
1.) Monitorar
 Observar a variabilidade de uma determinada característica do
processo;
 2.) Identificar (caracterizar)
Detectar causas que geram instabilidade (causas especiais);
 3.) Tomar ações
Prevenir as causas de instabilidade.

18. Variabili
dade
É o conjunto de diferenças nas medidas (cor, espessura,
peso, densidade, etc) presentes nos produtos ou serviços
resultantes de qualquer atividade.

19. Causas de Variação
no Processo
1.) Causas Comuns de Variação:
- Muitas causas que individualmente têm pouca influência;
- Pequena variação produzida;
- Processo suficientemente estável (previsível).
2.) Causas Especiais de Variação:
- Poucas causas que individualmente podem produzir
grandes variações
- Processo instável (imprevisível).

20. Processo sob
Controle
1.) Um processo está sob CONTROLE estatístico quando as
CAUSAS ASSINALÁVEIS DE VARIAÇÃO não
existem ou foram eliminadas e sua variabilidade é devida
exclusivamente às CAUSAS COMUNS;
2.) Estar sob CONTROLE é ser ESTÁVEL (ou PREVISÍVEL).

21. •Houver 2 pontos, em 3 sucessivos, de um mesmo lado da linha central, na zona
A ou acima desta;
•4 pontos, em 5 sucessivos, de um mesmo lado da linha central, na zona B ou
acima desta;
•9 pontos sucessivos de um mesmo lado da linha central;
•6 pontos consecutivos, ascendentes ou descendentes;
•14 pontos em uma série, alternando para cima e para baixo;
•15 pontos em uma série, dentro da zona C (acima ou abaixo da linha central).
O processo é dito “fora de controle” se:
1Um ou mais pontos caem fora dos
limites de controle;
2Quando se dividir a carta de controle
em zonas e:
Processo fora
de Controle

22. 6 pontos consistentemente crescendo ou
decrescendo
14 pontos em seqüência, alternando altos e
baixos
2 pontos (de 3) muito próximos ao limite
superior ou ao limite inferior
4 pontos (de 5) acima (ou abaixo) da metade
da faixa superior (ou inferior) de controle
8 pontos em seqüência, alternados acima e
abaixo da linha central e nenhum deles
próximo ao centro
Outras
condições que
podem indicar
presença de
causas
especiais

23. Em qualquer um desses casos, deve-se
observar e investigar o que mudou e,
possivelmente, fazer ajustes no
processo.

24. Cartas de
Controle
( sob
controle )

25. Cartas sob controle:
1.
2.
A maioria dos pontosflutuam
próximo da linha central;
Poucos pontos perto dolimite
de controle;
3.
4.
Nenhum ponto fora dos limites de
controle;
Não há seqüência de sete pontos em um
dos lados da linha média;
5.
pontos
Não há seqüência de sete (ou mais)
consecutivos crescente ou decrescente.
Carta para Indivíduos (%O2)
4
3,5
3
2,5
2
1,5
1
0,5
0
22-Ago
23-Ago
25-Ago
26-Ago
27-Ago
29-Ago
29-Ago
30-Ago
1-Set
3-Set
4-Set
6-Set
7-Set
9-Set
%O2
média
LSC
LIC
Carta de Amplitude Móvel (%O2)
1,40
1,20
1,00
0,80
0,60
0,40
0,20
0,00
22-Ago
23-Ago
25-Ago
26-Ago
27-Ago
29-Ago
29-Ago
30-Ago
1-Se
t
3-Se
t
4-Se
t
6-Se
t
7-Se
t
9-Se
t
R
R-médio
LSCR
LICR

26. Cartas de
Controle
( fora de
controle )

27. Carta
para
Indivíduos
(%O2
)
0,50
1,00
1,50
2,00
2,50
3,00
3,50
4,00
20-Ago
21-Ago
22-Ago
23-Ago
25-Ago
26-Ago
27-Ago
28-Ago
29-Ago
30-Ago
31-Ago
2-Set
3-Set
4-Set
%O2
Médi
a
LS
C
LIC
Carta
para
Indivíduos
(%O2
)
0,5
2
1,5
1
3,5
3
2,5
4
4,5
20-Ago
21-Ago
22-Ago
23-Ago
25-Ago
26-Ago
27-Ago
28-Ago
29-Ago
30-Ago
31-Ago
2-Set
3-Set
4-Set
%O2
Médi
a
LS
C
LIC
Carta
de
Amplitude
Móvel
(%O2)
0,00
0,50
1,00
1,50
2,00
2,50
20-Ago
21-Ago
22-Ago
23-Ago
25-Ago
26-Ago
27-Ago
28-Ago
29-Ago
30-Ago
31-Ago
2-Set
3-Set
4-Set
R
R-
médio
LSC
R
LICR
Carta
para
Indivíduos
(%O2
)
5,5
5
4,5
4
3,5
3
2,5
2
1,5
1
0,5
20-Ago
21-Ago
22-Ago
23-Ago
25-Ago
26-Ago
27-Ago
28-Ago
29-Ago
30-Ago
31-Ago
2-Set
3-Set
4-Set
%O2
Médi
a
LSC
LIC
B.
D.
A.
C.

28. x
Exercício: construir as cartas e
R para os dados: variações na
dimensão de uma peça, em
mm.
Hora
Am
os-
tras
8:00 8:30 9:00 9:30 10:00 10:30 11:00 11:30 12:00 12:30
1 -2 +1 +3 +2 -4 0 -1 -3 -6 +2
2 -2 0 +1 +3 -3 0 +1 +2 +2 -1
3 0 -1 -3 +5 0 -1 +2 -2 0 0
4 0 -1 +1 +2 +1 +1 -1 +1 +4 +1
5 -2 +1 0 +2 +3 -4 +3 +1 +4 +1
R

29. n c4 d2 d3 A2 A3 B3 B4 D3 D4
2 0.798 1.128 0.853 1.880 2.659 0 3.267 0 3.267
3 0.886 1.693 0.888 1.023 1.954 0 2.568 0 2.575
4 0.921 2.059 0.88 0.729 1.628 0 2.266 0 2.282
5 0.940 2.326 0.864 0.577 1.427 0 2.089 0 2.115
6 0.952 2.534 0.848 0.483 1.287 0.030 1.970 0 2.004
10 0.973 3.078 0.797 0.308 0.975 0.248 1.716 0.223 1.777
15 0.982 3.472 0.756 0.223 0.789 0.428 1.572 0.347 1.653
20 0.987 3.735 0.729 0.180 0.680 0.510 1.490 0.415 1.585
25 0.990 3.931 0.708 0.153 0.606 0.565 1.435 0.459 1.541
Fatores de correção
para cartas e
R

30. x
Exercício: construir as cartas e R
para os dados: variações na dimensão
de uma peça, em mm. SOLUÇÃO
Hora
Am
os-
tras
8:00 8:30 9:00 9:30 10:00 10:30 11:00 11:30 12:00 12:30
1 -2 +1 +3 +2 -4 0 -1 -3 -6 +2
2 -2 0 +1 +3 -3 0 +1 +2 +2 -1
3 0 -1 -3 +5 0 -1 +2 -2 0 0
4 0 -1 +1 +2 +1 +1 -1 +1 +4 +1
5 -2 +1 0 +2 +3 -4 +3 +1 +4 +1
-1,2 0,0 +0,4 +2,8 -0,6 -0,8 +0,8 -0,2 +0,8 +0,6
R 2 2 6 3 7 5 4 5 10 3

31. Solução: carta de
controle por
variável- médias
= 2,972
= - 2,452

32. Carta x
4
3
2
1
0
-1
-2
-3
hora
mm
Médias
LCS
LIC
Média

33. Solu
ção
= 9,936
= 0

34. carta R
12
10
8
6
4
2
0
hora
mm
Amplitudes
LSC
LIC
Média R

35. Existem dois tipos de carta
de controle:
1. Por variáveis
2. De atributo – peça aprovada ou
reprovada.

36. Cartas de controle
por atributo
 Aplicado quando as amostras refletem características
qualitativas (ex.: aprovado/reprovado; defeituoso/não
defeituoso)

37. Cartas de controle
por atributo
Carta p: fração defeituosa

38. Cartas de controle
por atributo

39. Exe
mplo
Uma indústria fabricante de produtos
cerâmicos decidiu construir um gráfico de
controle p para a linha de produção de um
dos tipos de peças que ela fabrica. Com este
objetivo, foram coletadas 20 amostras de
tamanho n=100. O número de peças
defeituosas em cada amostra é apresentada
na tabela. As amostras foram numeradas de
acordo com a seqüência de produção.

40. Tabela: número de peças
defeituosas em
amostras de 100 peças cerâmicas
número da número de
amostra defeituosos
1 21
2 25
3 16
4 30
5 15
6 17
7 23
8 28
9 26
10 25
11 22
12 30
13 10
14 20
15 16
16 15
17 25
18 18
19 11
20 12

41. n c4 d2 d3 A2 A3 B3 B4 D3 D4
2 0.798 1.128 0.853 1.880 2.659 0 3.267 0 3.267
3 0.886 1.693 0.888 1.023 1.954 0 2.568 0 2.575
4 0.921 2.059 0.88 0.729 1.628 0 2.266 0 2.282
5 0.940 2.326 0.864 0.577 1.427 0 2.089 0 2.115
6 0.952 2.534 0.848 0.483 1.287 0.030 1.970 0 2.004
10 0.973 3.078 0.797 0.308 0.975 0.248 1.716 0.223 1.777
15 0.982 3.472 0.756 0.223 0.789 0.428 1.572 0.347 1.653
20 0.987 3.735 0.729 0.180 0.680 0.510 1.490 0.415 1.585
25 0.990 3.931 0.708 0.153 0.606 0.565 1.435 0.459 1.541
Fatores de correção
para cartas e
R

42. Solu
ção
= 405/(20x100)= 0,2025=20,25%
= 0,3230
= 0,0819

43. Solu
ção
1
3
5
7
9
11
13
15
17
19
Carta de controle por atributo
0,35
0,3
0,25
0,2
0,15
0,1
0,05
0
Lotes
Defeituosos
(%)
média p
LSC
LIC
Média

44. Capacidade
(“capabilidade”)
do processo

45.  Aplicação: quando se necessitar determinar se o processo, com
suas variações naturais, é capaz de atender às especificações
estabelecidas. Um processo “sob controle estatístico” pode
produzir peças rejeitáveis.
(“capabilidade”) do
processo

46.  A verdadeira melhoria de um processo é obtida através do
equilíbrio entre a repetibilidade, consistência e capacidade de
atender às especificações do projeto, mais conhecida como
capabilidade do processo.
(“capabilidade”) do
processo

47. 1.) Um processo é CAPAZ quando ele atende às
ESPECIFICAÇÕES;
2.) Medir a capacidade do processo é compará-lo aos LIMITES
DE ESPECIFICAÇÃO;
3.) Um processo pode estar sob CONTROLE e não ser CAPAZ?
Resposta: SIM !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

48. relacionando
controle e
capacidade
do processo

49. Carta para Indivíduos (%O2)
4,5
4
3,5
3
2,5
2
1,5
1
0,5
0
22-Ago
23-Ago
25-Ago
26-Ago
27-Ago
29-Ago
29-Ago
30-Ago
1-Set
3-Set
4-Set
6-Set
7-Set
9-Set
%O2
média
LSC
LIC
LIE
LSE
1.
Indicadores
CP
=
1,58809
CPs= 1,526555
CPi= 1,649625
CPK = 1,52656
Situação ótima. Os
gráficos mostram
estabilidade e as
especificações são
atendidas.
2.
4,5
4
3,5
3
2,5
2
1,5
1
0,5
0
22-Ago
23-Ago
25-Ago
26-Ago
27-Ago
29-Ago
29-Ago
30-Ago
1-Set
3-Set
4-Set
6-Set
7-Set
9-Set
%O2
média
LSC
LIC
LIE
LSE
Indicadores
CP
=
1,51573
CPs= 1,438347
CPi= 1,593119
CPK = 1,43835
Situação de alerta. O
processo está bom
agora, mas não está
estável. Deve-se fazer
gráficos para estabelecer
o controle.
Fora de Controle / Capaz:
Carta para Indivíduos (%O2)
Sob Controle /
Capaz:

50. 3.
Carta paraIndivíduos (%O2)
5
4,5
4
3,5
3
2,5
2
1,5
1
0,5
0
22-Ago
23-Ago
25-Ago
26-Ago
27-Ago
29-Ago
29-Ago
30-Ago
1-Set
3-Set
4-Set
6-Set
7-Set
9-Set
%O2
média
LSC
LIC
LIE
LSE
Indicadores
CP
=
0,93694
CPs= 0,697462
CPi= 1,176421
CPK = 0,69746
Mudanças significativas
são necessárias no
processo.
Sob Controle / Não
Capaz: 4
.
Fora de Controle / Não Capaz:
Cartapara Indivíduos (%O2)
1
0
3
2
4
5
6
22-Ago
23-Ago
25-Ago
26-Ago
27-Ago
29-Ago
29-Ago
30-Ago
1-Set
3-Set
4-Set
6-Set
7-Set
9-Set
%O2
média
LSC
LIC
LIE
LSE
Indicadores
CP
=
0,81888
CPs= 0,675005
CPi= 0,962747
CPK = 0,67501
Situação péssima.
Mudanças drásticas
são necessárias, além
da eliminação das
causas especiais.

51. Avaliando a
capacidade
potencial do
processo (Cp)

52. Cp: Capacidade potencial do processo, ou seja mede
o potencial do processo atender às especificações.
Cp =
Faixa de Tolerância da Especificações
Faixa de Tolerância Natural do Processo
Processo confiável tem Cp maior ou igual a 1,33
Exemplos:
Se Cp = 2,0
Se Cp = 1,0
A faixa de especificação é duas vezes mais ampla
que a faixa de dispersão do processo
A faixa de especificação é a mesma que a faixa
de dispersão do processo

53. calcular os índices
de capabilidade do
processo
Cp= índice que relaciona a amplitude
permitida dos limites de especificação
para analisar a real variabilidade do pro-
cesso representado por , onde
é o desvio padrão do processo
Onde: = média das amplitudes nos subgrupos
= valor tabelado e baseado no tamanho da amostra
do subgrupo

54. Processo capaz e centrado:
Mais de 99.74% do produzidoé
conforme.
Processo não capaz e centrado:
Produz desconformidades acima
e abaixo das tolerâncias.
Processo capaz e não centrado:
Produz desconformidades acima
da tolerânciasuperior.
Processo não capaz e não centrado:
Produz desconformidades acima e
abaixo das tolerâncias.
Situações possíveis
do processo

55. Porém, o parâmetro Cp não indica se a
média do processo está centrada.
Logo, Cp indica somente o “potencial”
do processo.
Os índices de capabilidade do processo
Cpi e Cps (para limites unilaterais de
especificação) e Cpk (para limites
bilaterais da especificação) não só
medem a variação do processo como
também consideram a posição média do
processo.

56. Então, o Cpk é considerado como uma
medida da “capabilidade do processo” e
utiliza o menor dos índices Cpi e Cps.

57. processo em
função do
Cpk
Fonte: José Luiz Ribeiro e Carla Ten Caten

58. Atacando
as falhas
Priorizar: atacar de primeiro as falhas com maiores
potenciais de impacto na Operação.
Buscar as causas-raízes das falhas: utilizar para isso
as ferramentas da qualidade.
Identificar ações de melhoramento.
Planejar, programar e executar as ações de
melhoramento: centrar as ações na prevenção.
Estabelecer indicadores e formalizar procedimentos.
Registrar e acompanhar os resultados.
Corrigir ações e procedimentos, se necessário.

59. Obrigada!