Análise dos parâmetros e cálculo da eficiência de uma hélice para aeromodelos
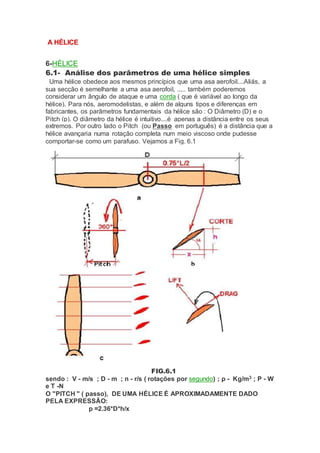
- 1. A HÈLICE 6-HÉLICE 6.1- Análise dos parâmetros de uma hélice simples Uma hélice obedece aos mesmos princípios que uma asa aerofoil....Aliás, a sua secção é semelhante a uma asa aerofoil, ..... também poderemos considerar um ângulo de ataque e uma corda ( que é variável ao longo da hélice). Para nós, aeromodelistas, e além de alguns tipos e diferenças em fabricantes, os parâmetros fundamentais da hélice são : O Diâmetro (D) e o Pitch (p). O diâmetro da hélice é intuitivo....é apenas a distância entre os seus extremos. Por outro lado o Pitch (ou Passo em português) é a distância que a hélice avançaria numa rotação completa num meio viscoso onde pudesse comportar-se como um parafuso. Vejamos a Fig. 6.1 FIG.6.1 sendo : V - m/s ; D - m ; n - r/s ( rotações por segundo) ; ρ - Kg/m3 ; P - W e T -N O "PITCH " ( passo), DE UMA HÉLICE É APROXIMADAMENTE DADO PELA EXPRESSÃO: p =2.36*D*h/x
- 2. Pitch(p) = 2.36x diâmetro(D) x altura(h)/largura(x) ……..( FiG.6.1-b) Note-se que estes valores vão variando ao logo da hélice, do cubo para a ponta, o que se justifica pela variação da velocidade da secção da hélice com a sua distância ao centro. PARA CADA SECÇÃO TEMOS DUAS VARIÀVEI IMPORTANTES : A CORDA e O ÂNGULO α, (Figura 6.1-b) A secção onde medimos o h e o x para calcular o valor do pitch fica situada a 75% do raio, a partir do centro e é uma questão de referência, sendo a geralmente a usada. Se seccionarmos a hélice a várias distâncias do centro, vamos obter cortes de perfis tipo alar aerofoil. Então, se o perfil é aerofoil teremos mais duas variáveis importantes no desempenho da hélice: OS VALORES DE CL E CD para a pá Isto dá-nos uma ideia da complexidade de uma hélice e do seu tratamento físico – matemático, assunto que não abordaremos! 6.2- Algumas regras práticas Podemos referir, em relação a estes aspectos geométricos algumas regras empíricas , nomeadamente no respeitante ao Pitch: Hélices com Pitch elevado Velocidade de voo alta Dificuldade de aceleração Dificuldade de subida Dificuldade de abrandamento para aterragem Hélices com Pitch baixo Velocidade de voo baixa Boa aceleração Boa capacidade de subida Possibilidade de controlo " fino" da velocidade Muitos fabricantes de motores indicam-nos a o tamanho ideal da hélice para esse motor, por exemplo10 x 6 ( polegadas).Se este for um tamanho criterioso, a prática indica também que poderemos usar nesse motor, hélices dos seguintes tamanhos: 8 x 8 9 x 7 10 x 6 11 x 5 12 x 4 Ou seja, diminuindo uma unidade ao diâmetro e aumentado uma unidade ao Pitch (e vice versa) ás dimensões standart. Uma outra regra prática muito difundida é que o pitch deverá estar entr 1/2 x e 1 x o diâmetro. Vamos agora fazer uns pequenos cálculos que o mínimo que podemos chamar é primitivos: EM TODOS OS EXEMPLOS QUE SE SEGUEM VAMOS REFERIR-NOS A UMA HÉLICE APC de 7 x 4"
- 3. 6.3 - Cálculo da velocidade teórica Hélice de 4 x 7 ", 100% eficiente, montada num motor de 15000 rpm, num avião com drag=0. Nesse caso ideal teremos rps=15000/60=250 rps. A velocidade que resultaria se a hélice avançasse o seu número de rotações/s x o seu passo seria V = rps*p = 250 *7" = 1750 " = 44.45 m/s V = m/s * 3600 = 44.45 x 3600= 160020 m/h = 160 Km/h Mas a eficiência da hélice vai baixar este número drasticamente, para metade ou menos. Há uma grande diferença entre a potência que a hélice recebe do motor e a que resulta em energia propulsora 4.6- Cálculo prático da eficiência da hélice Para tal temos que fazer um teste de velocidade. Suponhamos que em campo, o nosso modelo percorre 1000 m em 35 s . Isto corresponde a 28.57 m/s. A razão entre este valor e o anterior é 28.57/44.45 = 0.64 →64% Ou seja, a nossa hélice está a trabalhar com uma eficiência de 64% o que é bastante vulgar ( Claro que estamos a cometer um erro, que é comparar uma velocidade real que depende de muitos factores , com uma velocidade teórica dependendo apenas da hélice e dos rpm). A potência necessária para a hélice trabalhar a dados rpm pode ser obtida por : P = k* rpm3* D4 *p.................( Stefan Verkoeter) Potência(P)=k*rpm3 *Diâmetro(D)4 *Pitch(p) sendo, para a generalidade das hélices , k uma constante de aprox. k= 5.3x10-15 . De notar que esta é uma expressão empírica criada pelo autor a partir de cerca de 50 ensaios, portanto os seus resultados estarão afectados de certo erro para cada caso em particular. Mais á frente veremos a magnitude do erro para um caso ( apenas) THRUST ou TRACÇÃO - É a força de impulso produzida pelo hélice . Vamos manter a designação inglesa para esta força, que será representada por FT. O funcionamento básico da hélice está sumariamente representado na figura seguiinte:
- 4. FIG.6.2 O ar é captado na parte da frente da hélice, movimentado através do "disco" que ela desenha no seu movimento com uma velocidade Vf...Suponhamos que o nosso modelo está a voar num dia calmo, sem vento....Então VF será a própria velocidade do modelo como é obvio.O ar é expelido para trás da hélice, animado de um acréscimo de velocidade ΔV, sendo então - Vp, - a velocidade com que o ar passa através da hélice. Sucintamente a hélice vai acelerar o movimento do ar e como, a massa de ar que "entra na zona do disco" e a que sai é a mesma, obviamente o fluxo de ar á saída da hélice é mais estreito e, assim sendo a velocidade de esteira a certa distância da hélice, Vw -será ainda maior. Teremos Vw>Vp>Vf.Ao mesmo tempo, a hélice vai provocar um movimento de rotação no ar que passa através dela , que é energia perdida , pois não concorre para o Impulso. (geralmente é 1 a 5% de perda de potência aplicada). No nosso caso de aeromodelistas considero a hélice, a parte do modelo mais difícil de abordar. A potência que o eixo do motor transmite á hélice vai transformar-se em ganho de energia cinética do ar que passa através da hélice. Nessa transformação está um dos mais baixos rendimentos de toda a electromecânica do aeromodelo. Em termos de valores importantes referentes á energia fornecida pela hélice podemos considerar, face ás suas características aerodinâmicas as seguintes grandezas: a velocidade, portanto a eficiência da hélice aproxima-se de 0, ( zero), quando a velocidade do avião baixa. As figuras seguintes mostram os valores de CT e CP para algumas geometrias de hélice.
- 5. FIG.6.3 FIG.6.4 A eficiência de uma hélice , depende da velocidade, portanto a eficiência da hélice aproxima-se de 0, ( zero), quando a velocidade do avião baixa. A fig. seguinte mostra a eficiência η de uma hélice num avião de competição, em função do avanço:
- 6. Note-se por esta curva, que, se considerarmos uma hélice com determinado D, rodando a rotações n, o seu rendimento vai variar com a velocidade crescendo com esta até ao valor V/(nD)= 0.7, onde tem o rendimento máximo e voltando a descer após esse valor . O rendimento que a hélice tem durante um voo não vai ser constante Pelo já dito vemos as dificuldades intrínsecas no estudo das Hélices, mas a sua importância é enorme pois vão determinar o impulso a que o aeromodelo vai estar sujeito, que é essencial para o seu movimento e sustentação Definimos Impulso ou Thrust Estático- Te-, como o Thrust desenvolvido pela hélice com o avião parado, pois nesse caso não há nenhuma corrente de ar de velocidade V indo de frente contra a hélice . Suponhamos que imobilizamos um modelo e o pomos a funcionar a potência máxima. Nesse caso, a velocidade VF é muito baixa e desprezável, pois o movimento do ar na parte da frente da hélice deve-se apenas a um efeito de aspiração que é muito fraco, ( atendamos á fig.2). Deste modo, toda a velocidade que o ar adquire para o lado de trás da hélice é resultante da actividade desta, ou seja V+ΔV é apenas ΔV da hélice e o esforço é máximo. É por isso que nestas condições também o valor do Imput em Watts . Se, porém, o avião está a mover-se com uma velocidade V, então há uma corrente de ar de velocidade V que está a ir contra o "disco da hélice", levando a que , por parte da hélice, esta tenha de criar menos aceleração para obter uma velocidade necessária do ar a jusante. O conhecimento deste valor é importante, pois na prática deverá ser não menos que 1/3 do peso do modelo. Um rácio de Te/peso de pelo menos 0.4/1 é necessário para que o modelo tenha possibilidades de levantar do chão, da relva, por exemplo. Para uma dada potência, quanto maior for o thrust que tenhamos, mais baixa vai ser a velocidade máxima do modelo: Para a mesma potência : Maior diâmetro e menor pitch = maior Thrust e menor velocidade Menor diâmetro e maior pitch = menor Thrust e maior velocidade Uma hélice mais pequena requer mais potência para produzir o mesmo thrust que uma maior. por exemplo: uma hélice Aeronaut 12x7 absorve 85 W para produzir 756 g de thrust a 6000 rpm. Para produzir o mesmo thrust uma hélice de 6x5 necessita de cerca de 195W a 18000 rpm Velocidade estática -Ve- è igual ao valor de rpm* pitch da hélice. Este valor deverá ser cerca de 2.5 x o valor da velocidade de estol do modelo
- 7. Tentámos encontrar algo que permitisse um cálculo fácil do Thrust , mas em quase todos os casos fomos travados pela necessidade de conhecer parâmetros apenas determináveis experimentalmente em túneis de vento. Encontramos dois programas on-line, respectivamente: 1- http://www.adamone.rchomepage.com/calc_motor.htm 2 -http://personal.osi.hu/fuzesisz/strc_eng/index.htm No capítulo de MOTORIZAÇÃO Tentaremos melhorar as possibilidades de cálculo