Este documento apresenta um resumo das principais ideias sobre proposições simples e compostas em lógica matemática. Em 3 frases ou menos:
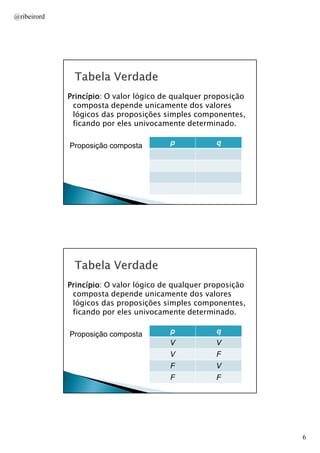
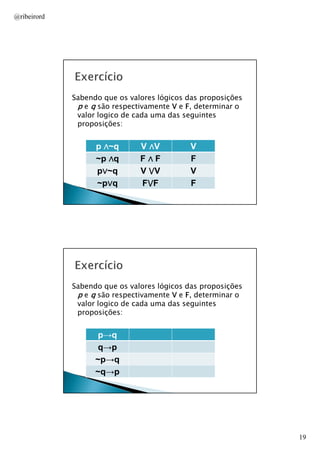
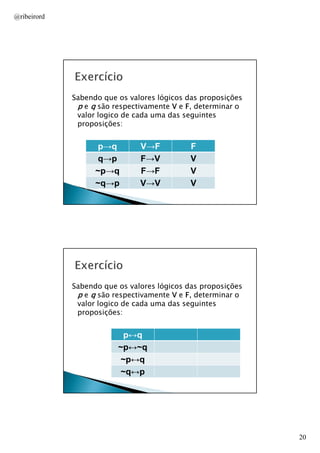
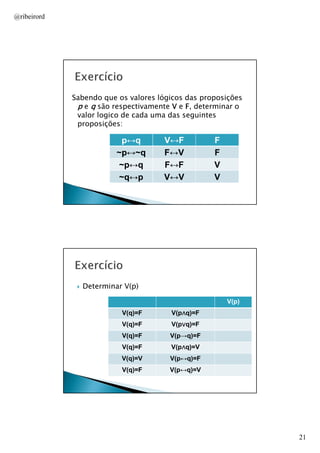
Define proposições como expressões que transmitem um pensamento completo e introduz os conceitos de proposições simples, compostas e seus valores lógicos de verdade e falsidade. Apresenta os principais conectivos lógicos como negação, conjunção, disjunção, implicação e bicondicional e explica como eles determinam o valor lógico de proposições compostas