Este documento apresenta conceitos fundamentais da estática dos fluidos, incluindo:
1) A definição de fluido e as características dos fluidos ideais e incompressíveis.
2) As diferenças entre os estados líquido e gasoso em termos de arranjo molecular, compressibilidade e interações.
3) O conceito de densidade e densidade relativa, ilustrado com exemplos.
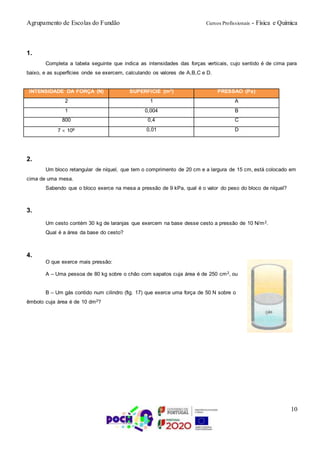
4) A definição de pressão e suas unidades de medida.