1) O documento discute sistemas lineares, incluindo definição, classificação, e métodos de resolução como gráfico, igualação, substituição e redução.
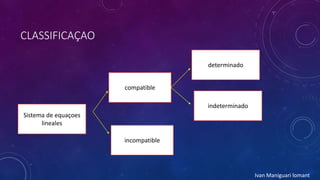
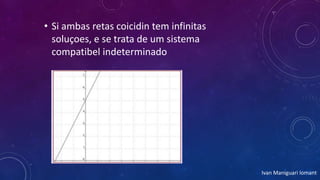
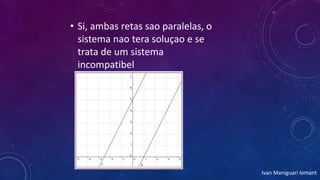
2) Os sistemas lineares podem ser classificados como compatível determinado, compatível indeterminado ou incompatível.
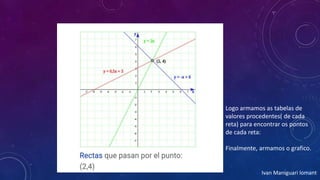
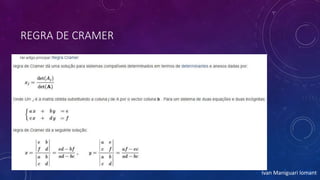
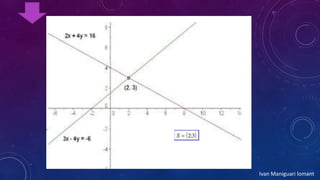
3) Os métodos de resolução incluem abordagens gráficas, igualação, substituição e redução para encontrar soluções.