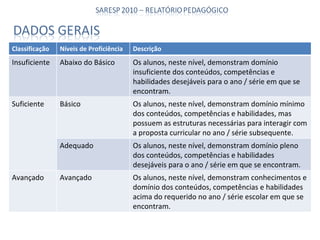
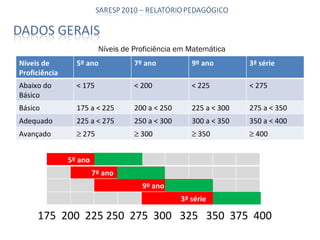
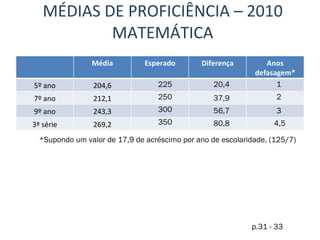
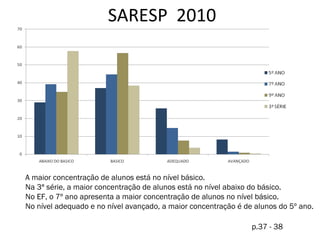
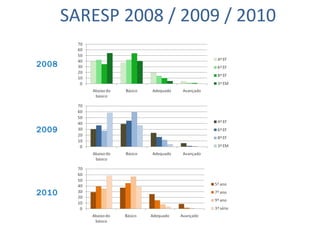
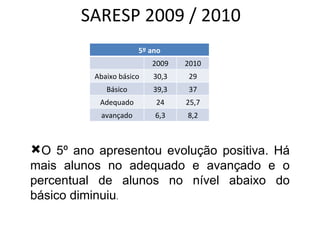
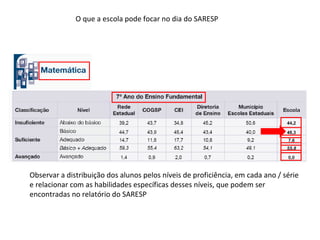
O documento apresenta os resultados do SARESP 2010 para Matemática. Ele descreve a metodologia de avaliação, apresenta os níveis de proficiência e suas respectivas habilidades, e analisa os resultados obtidos pelos alunos do 5o, 7o, 9o anos do ensino fundamental e 3a série do ensino médio.

1. RELATÓRIO PEDAGÓGICO SARESP 2010 MATEMÁTICA CENP

6. Classificação Níveis de Proficiência Descrição Insuficiente Abaixo do Básico Os alunos, neste nível, demonstram domínio insuficiente dos conteúdos, competências e habilidades desejáveis para o ano / série em que se encontram. Suficiente Básico Os alunos, neste nível, demonstram domínio mínimo dos conteúdos, competências e habilidades, mas possuem as estruturas necessárias para interagir com a proposta curricular no ano / série subsequente. Adequado Os alunos, neste nível, demonstram domínio pleno dos conteúdos, competências e habilidades desejáveis para o ano / série em que se encontram. Avançado Avançado Os alunos, neste nível, demonstram conhecimentos e domínio dos conteúdos, competências e habilidades acima do requerido no ano / série escolar em que se encontram.

7. 175 200 225 250 275 300 325 350 375 400 Níveis de Proficiência em Matemática Níveis de Proficiência 5º ano 7º ano 9º ano 3ª série Abaixo do Básico < 175 < 200 < 225 < 275 Básico 175 a < 225 200 a < 250 225 a < 300 275 a < 350 Adequado 225 a < 275 250 a < 300 300 a < 350 350 a < 400 Avançado  275  300  350  400 5º ano 7º ano 9º ano 3ª série

8. RESULTADOS

9. MÉDIAS DE PROFICIÊNCIA – 2010 MATEMÁTICA *Supondo um valor de 17,9 de acréscimo por ano de escolaridade, (125/7) p.31 - 33 20,4 37,9 56,7 80,8 4,5 3 2 1 225 250 300 350 Média Esperado Diferença Anos defasagem* 5º ano 204,6 7º ano 212,1 9º ano 243,3 3ª série 269,2

10. SARESP 2010 A maior concentração de alunos está no nível básico. Na 3ª série, a maior concentração de alunos está no nível abaixo do básico. No EF, o 7º ano apresenta a maior concentração de alunos no nível básico. No nível adequado e no nível avançado, a maior concentração é de alunos do 5º ano. p.37 - 38

11. SARESP 2008 / 2009 / 2010 2008 2009 2010

21. O que a escola pode focar no dia do SARESP Comparar também com os níveis esperados para cada ano / série Juvenal de Gouveia - Eq. Técnica Mat. - SEE 28,5 pontos 2 ano (300 – 200) : 7  14 pontos / ano 67 pontos 3,5 anos (350 – 225) : 7  18 pontos / ano 93 pontos 4,5 anos (350 – 250) : 5  20 pontos / ano Níveis esperados (adequados) 5º ano 7º ano 9º ano 3ª série LP 200 225 275 300 MAT 225 250 300 350 CCN - 250 300 350

28. O que a escola pode focar no dia do SARESP Observar a distribuição dos alunos pelos níveis de proficiência, em cada ano / série e relacionar com as habilidades específicas desses níveis, que podem ser encontradas no relatório do SARESP

31. Exemplo de item que esse aluno faz: P. 102 GAB % de resposta C A B C D 10 14,9 60,2 15

32. Exemplo de item que esse aluno não faz: P. 124 GAB % de resposta C A B C D 12,2 13,7 13,3 60,8