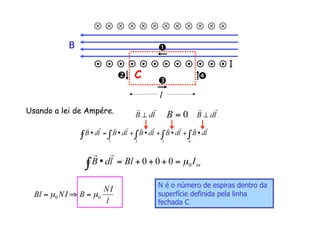
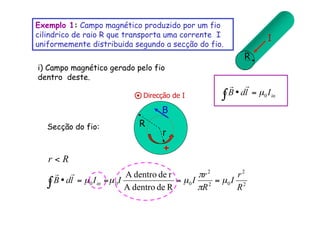
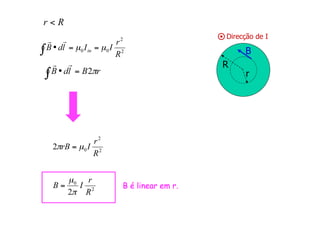
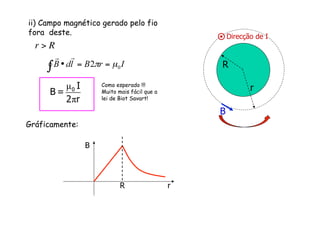
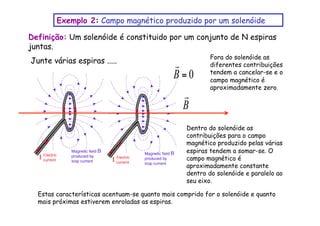
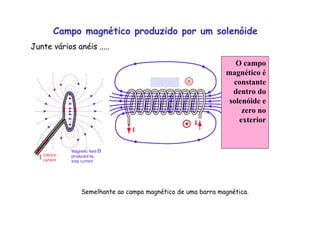
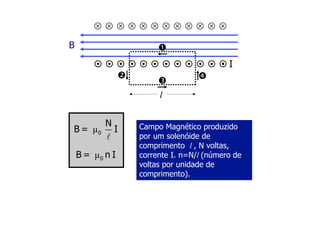
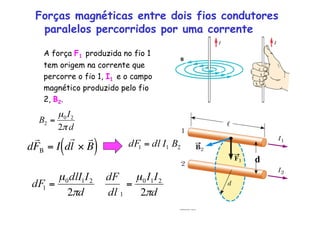
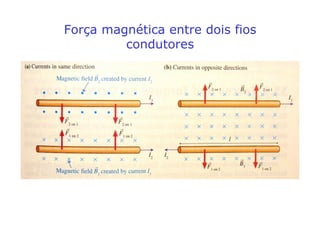
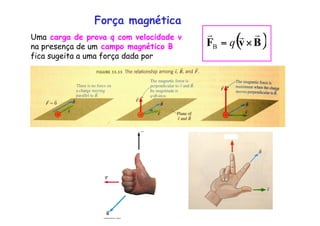
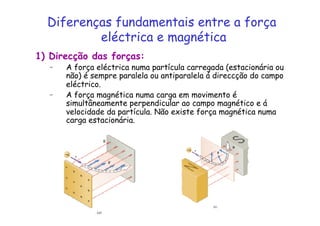
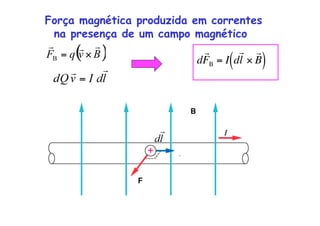
O documento descreve conceitos fundamentais de eletromagnetismo, incluindo: 1) A lei de Ampère, que relaciona o campo magnético gerado por correntes elétricas com a corrente total atravessando uma superfície fechada. 2) O campo magnético produzido por um fio cilíndrico e por um solenóide, composto por várias espiras de fio juntas. 3) A definição de força magnética em uma carga em movimento na presença de um campo magnético.

1. EO- Sumário 12
Raquel Crespo
Departamento Física, IST-Tagus Park

2. I é a corrente total que atravessa a
superfície limitada pela linha fechada.
A lei de Ampére é util para calcular o campo
magnético gerado por correntes com simetria.
Lei de Ampére
€

B• d

l∫ = µ0 Iin
Integral de linha !

3. Exemplo 1: Campo magnético produzido por um fio
cilindrico de raio R que transporta uma corrente I
uniformemente distribuida segundo a secção do fio.
I
R
Secção do fio: R
r
Direcção de I
B
i) Campo magnético gerado pelo fio
dentro deste.
+

4. R
r
Direcção de I
B
B é linear em r.

5. R
r
Direcção de I
B
B
rR
Gráficamente:
Como esperado !!!
Muito mais fácil que a
lei de Biot Savart!
ii) Campo magnético gerado pelo fio
fora deste.
€
r > R

6. Junte várias espiras .....
Dentro do solenóide as
contribuições para o campo
magnético produzido pelas várias
espiras tendem a somar-se. O
campo magnético é
aproximadamente constante
dentro do solenóide e paralelo ao
seu eixo.
Definição: Um solenóide é constituido por um conjunto de N espiras
juntas.
Fora do solenóide as
diferentes contribuições
tendem a cancelar-se e o
campo magnético é
aproximadamente zero.
Estas características acentuam-se quanto mais comprido for o solenóide e quanto
mais próximas estiverem enroladas as espiras.
Exemplo 2: Campo magnético produzido por um solenóide

7. Junte vários anéis .....
Semelhante ao campo magnético de uma barra magnética.
Campo magnético produzido por um solenóide
O campo
magnético é
constante
dentro do
solenóide e
zero no
exterior



8. Usando a lei de Ampére.
           
           
B
I



l
N é o número de espiras dentro da
superfície definida pela linha
fechada C
C

9.            
           
B
I



l
Campo Magnético produzido
por um solenóide de
comprimento l , N voltas,
corrente I. n=N/l (número de
voltas por unidade de
comprimento).

10. Força magnética
Uma carga de prova q com velocidade v
na presença de um campo magnético B
fica sugeita a uma força dada por

11. Diferenças fundamentais entre a força
eléctrica e magnética
1) Direcção das forças:
– A força eléctrica numa partícula carregada (estacionária ou
não) é sempre paralela ou antiparalela á direccção do campo
eléctrico.
– A força magnética numa carga em movimento é
simultâneamente perpendicular ao campo magnético e á
velocidade da partícula. Não existe força magnética numa
carga estacionária.

12. 2) Trabalho realizado pela força na partícula:
– A força eléctrica pode realizar trabalho numa partícula
e fazer variar a sua energia cinética.
– A força magnética não pode realizar trabalho e fazer
variar a energia cinética da partícula carregada.
Diferenças fundamentais entre a
força eléctrica e magnética

13. Força magnética produzida em correntes
na presença de um campo magnético
€
d

FB = I d

l ×

B( )

14. A força F1 produzida no fio 1
tem origem na corrente que
percorre o fio 1, I1 e o campo
magnético produzido pelo fio
2, B2.
d
Forças magnéticas entre dois fios condutores
paralelos percorridos por uma corrente
d

FB = I d

l ×

B( )

15. Força magnética entre dois fios
condutores