1) O relatório descreve as atividades do Grupo de Estudo sobre Jogos Matemáticos da Universidade Estadual Paulista em 2008, incluindo eventos expositivos e participação em conferências científicas.
2) Foram publicados 25 trabalhos científicos sobre o uso de jogos como ferramenta complementar no ensino de matemática em 5 eventos diferentes.
3) O grupo realizou uma apresentação expositiva chamada "Venha nos Conhecer" e continuou pesquisando novos jogos matemáticos para aplicação no ensino




















![Atividades Matemáticas Envolvendo Jogos – Uma
Modificação no Ensino
Alessandra B. Altran, Dalva M. O. Villarreal, Mara L. M. Lopes
Depto de Matemática, FEIS, UNESP
15385-000, Ilha Solteira, SP
E-mail: lealtran@mat.feis.unesp.br, dalva@mat.feis.unesp.br, mara@mat.feis.unesp.br
O objetivo deste trabalho é relatar a jogo para a vida da criança, do jovem e do
experiência da utilização de jogos adulto [2].
matemáticos como uma alternativa à Este tipo de formação é inexistente
metodologia tradicional do ensino de nos currículos oficiais dos cursos de formação
matemática. Para tanto, será apresentado o de educadores, entretanto, algumas
desenvolvimento do trabalho envolvendo, experiências mostram sua validade; e não são
tanto os alunos do curso de Licenciatura em poucos que afirmam ser a ludicidade a
Matemática, da Unesp de Ilha Solteira, quanto alavanca da educação para o terceiro milênio
os alunos da rede municipal de ensino do [7]. Porém, vale ressaltar que a utilização dos
município de Ilha Solteira (SP) e Selvíria jogos não é uma novidade no processo
(MS). Serão apresentadas, ainda, as educacional. A literatura mostra que na
contribuições dessa atividade em relação às antiguidade essa ferramenta já era utilizada.
escolas de ensino fundamental e, Muitos são os registros da contribuição da
principalmente, ao estudante universitário, atividade lúdica, mais especificamente, os
através da experiência prática adquirida com a jogos. Porém, ainda hoje, é pouco comum
atividade na qual está sendo formado para encontrar escolas que fazem uso desse recurso,
desenvolver. mesmo estando em destaque nos Parâmetros
Curriculares Nacionais (PCN). Segundo os
Introdução PCN, não existe um caminho único e melhor
para o ensino da Matemática, veja o trecho a
A atividade lúdica é, essencialmente, seguir:
um grande laboratório em que ocorrem ''Finalmente, um aspecto relevante nos
experiências inteligentes e reflexivas, jogos é o desafio genuíno que eles provocam
propiciando a aquisição de conhecimento. no aluno, que gera interesse e prazer. Por isso,
Assim, ocorre a preocupação de complementar é importante que os jogos façam parte da
o processo educativo dos futuros educadores, cultura escolar, cabendo ao professor analisar
ou seja, deseja-se fazer com que os alunos do e avaliar a potencialidade educativa dos
curso de Licenciatura em Matemática, desde o diferentes jogos e o aspecto curricular que se
inicio do curso, tenham contato com as deseja desenvolver'' [8].
ferramentas pedagógicas alternativas. Assim, de forma a modificar essa
A formação lúdica possibilita o realidade, objetiva-se a utilização dos jogos
desenvolvimento de certas habilidades matemáticos como ferramenta facilitadora de
imprescindíveis para o aprendizado de aprendizagem; considerando que, conhecer as
Matemática e para a resolução de problemas possibilidades de trabalho em sala de aula é
em geral, tais como, organização, atenção e fundamental para que o professor construa sua
concentração [1]. Existem jogos que encerram prática. Portanto, esta é uma proposta que
em suas soluções lições valiosas, muito atinge tanto o educando, quanto o futuro
semelhantes à resolução sistemática de educador.
problemas.
Além disso, a atividade lúdica leva o Iniciativa
educador a conhecer-se como pessoa, saber de
suas possibilidades, desbloquear resistências e Em 2006, ocorreu a primeira proposta
ter uma visão clara sobre a importância do de estudo sobre jogos matemáticos. Para tanto,](https://image.slidesharecdn.com/03relatorio2008-110906153354-phpapp02/85/Relatorio-de-Atividades-2008-21-320.jpg)
![foi organizado um grupo, composto por alunos composto por doze alunos, do curso de
do primeiro ano do curso de Matemática. Licenciatura em Matemática (ingressantes em
Foram estudados alguns jogos que o LEM 2007) e por três professores do departamento
(Laboratório de Ensino de Matemática) de Matemática
dispunha; tais como, Torre de Hanói, A primeira etapa do trabalho foi
Quadrado Mágico e Tangram. Porém, tal composta pela realização do levantamento dos
pesquisa foi realizada de forma bastante jogos que o LEM dispunha, e a seleção de
superficial, pois, os alunos ainda apresentavam quais seriam abordados, já que a primeira
dificuldades nos conceitos matemáticos proposta era a apresentação do referido
envolvidos. O resultado dessa pesquisa inicial evento. Foram selecionados quatro jogos
foi apresentado na Oficina “Jogos matemáticos: Quadrado Mágico, Kakuro,
Matemáticos”, na V Semana da Matemática Sudoku e Cubo Soma, com mostra a Figura 1.
desta instituição.
Em 2007, essa proposta foi retomada Quadrado Mágico Kakuro
quando as disciplinas Álgebra Elementar (1o
semestre) e Fundamentos de Matemática
Elementar (2o semestre), reformuladas de
modo a cumprir a exigência do MEC de
introduzir aulas teórico-práticas em algumas
disciplinas, fez uso dos jogos matemáticos
para evidenciar a aplicação da teoria estudada. Sudoku Cubo Soma
A princípio, a prática aplicada nas
disciplinas só tinha o propósito de cumprir os
preceitos determinados pelo MEC. Porém, um
convite realizado pela coordenação do curso
de Licenciatura em Matemática em oferecer,
em um evento promovido pelo próprio
departamento, uma oficina que abordasse Figura 1 – Jogos escolhidos para desenvolvimento da
jogos matemáticos, levou à formação do atividade
“Grupo de Estudo sobre Jogos Matemáticos”.
Desta vez, o trabalho se deu de forma bem Assim, houve a necessidade de dividir
elaborada, uma vez que os alunos já o grupo de forma a abordar os quatro temas,
apresentavam maior domínio das teorias formando assim, subgrupos de três alunos.
envolvidas, pelo fato de terem sido tratadas Apesar de cada grupo ter ficado responsável
nas disciplinas. por apenas um jogo, exigiu-se que os mesmos,
através dos demais, tomassem conhecimento
dos outros jogos, ou seja, de qualquer forma
Desenvolvimento da Proposta todos os alunos deveriam conhecer os quatro
jogos.
O trabalho objetivou a abordagem A primeira tarefa proposta ao grupo
apurada dos jogos matemáticos, como foi realizar o levantamento bibliográfico sobre
alternativa à metodologia tradicional do ensino a teoria envolvida e o estudo do método de
de matemática, ou seja, além de propor ao resolução de cada jogo. Os alunos utilizaram
grupo a pesquisa sobre a funcionalidade de os livros da biblioteca do campus e a internet.
cada jogo; propôs-se também, a abordagem de Durante esse processo surgiu idéia de
toda a fundamentação teórica e pedagógica levar o grupo ao atendimento direto aos alunos
envolvida. do ensino fundamental. Para tanto, foi
Com já mencionado anteriormente, o necessário fazer com que cada grupo tivesse
trabalho teve início com a formação do grupo, condições de confeccionar os jogos, pois, com
cujos alunos foram selecionados através da a livre manipulação de materiais variados, a
análise de seu desempenho nas atividades de criança passa a reconstituir e reinventar as
prática de ensino das disciplinas tratadas coisas, o que já exige uma adaptação mais
acima, ou seja, que apresentaram bom completa [3]. Assim, os alunos desenvolveram
desempenho e maior habilidade de expressão, uma pesquisa que os levou a estarem aptos à
colocação e didática. Assim, o grupo foi confecção de cada jogo. Durante esse processo](https://image.slidesharecdn.com/03relatorio2008-110906153354-phpapp02/85/Relatorio-de-Atividades-2008-22-320.jpg)

![comprometimento com seu ambiente de A atividade foi desenvolvida através
trabalho. da exposição dos jogos do LEM, da mesma
A apresentação foi realizada de forma forma que ocorreu na segunda atividade,
muito parecida à da primeira atividade, porém, dispostos em uma sala de aula, como
também foram abordados os jogos Cubo mostra a figura 5.
Soma, Kakuro, Sudoku e Quadrado Mágico,
porém, adaptados aos alunos de cada série, no Resultados
caso quarto e sexto ano, veja a figura 4.
A atividade envolvendo jogos
matemáticos trouxe muitos benefícios, pois,
foi possível comprovar que o jogo possibilita a
aproximação do sujeito ao conteúdo científico,
através da linguagem, informações,
significados culturais, compreensão de regras,
imitação, bem como pela ludicidade inerente
ao próprio jogo, assegurando assim, a
construção de conhecimentos mais elaborados
e interação social [5], [6].
Em relação aos alunos participantes do
grupo, por serem alunos do primeiro ano do
curso de Licenciatura em Matemática, levou-
se em consideração que os mesmos estavam
em fase de aprendizado e adaptação com as
atividades acadêmicas, assim, a interferência
da coordenação foi fundamental para o bom
Figura 4 – Fotos da visita à escola municipal Nelson
Duarte rocha
desenvolvimento das atividades.
Assim, durante todo o processo, os
Quarta Atividade alunos iam vencendo barreiras. Na primeira
“Colégio Anglo – Iha Solteira” etapa a maior dificuldade apontada por eles
(19 de novembro de 2007 - Ilha Solteira/SP) era encontrar material para fundamentar cada
jogo, já que esse tipo de abordagem não é
Como dito acima, após tomar muito usual. Já na segunda etapa, como era
conhecimento do trabalho desenvolvido pelo esperado, os alunos esbarraram no
grupo, o colégio Anglo fez um convite para preconceito, pois, a idéia de aprendizado
participação em uma atividade expositiva que voltado ao ensino, ainda não é uma das mais
envolvia pais, alunos e funcionários do próprio bem aceitas dentro de um ambiente cujo
colégio. contexto é voltado simplesmente à
aprendizagem do conteúdo, apesar de o curso
ser Licenciatura.
No geral, todos se comportaram muito
bem, atenderam às expectativas. Por ser um
primeiro contato com a atividade de pesquisa e
de docência, apresentaram certa insegurança,
que foi sendo minimizada ao passo que as
apresentações vinham ocorrendo. Vale
ressaltar que o modo com o qual os alunos
colocaram os jogos na tentativa de seduzir os
alunos, de forma a introduzir a teoria
matemática envolvida, foi surpreendente
Assim, foi notório o amadurecimento e
crescimento individual que essa atividade
provocou nesses alunos.
Agora, em relação aos alunos do
ensino fundamental, pouco se pode dizer, pois,
Figura 5 – Fotos da visita ao colégio Anglo - ISA foram realizadas apenas duas visitas e, em](https://image.slidesharecdn.com/03relatorio2008-110906153354-phpapp02/85/Relatorio-de-Atividades-2008-24-320.jpg)
![locais diferentes, mas, mesmo assim foi Perspectivas Futuras
possível observar o grande contentamento que
tal atividade trouxe aos alunos, comprovando Para o ano de 2008 a proposta é dar
a afirmação de Guzmán, que reforça que a continuidade ao trabalho, pois, ainda há muita
utilização de jogos no ensino de Matemática contribuição a ser dada. Como as atividades
não tem função apenas de divertir, mas sim, de nas escolas agradaram bastante, o grupo
extrair das atividades, materiais suficientes recebeu o convite de mais três escolas para a
para gerar conhecimento, interesse e fazer com apresentação do trabalho com jogos.
que os estudantes pensem com certa Sendo assim, objetiva-se realizar o
motivação [4]. atendimento a esses convites, de forma a
Pode-se dizer, ainda, que a atividade continuar contribuindo com sistema ensino;e,
provocou mudança na forma de pensar dos absorver os alunos do curso de matemática,
próprios professores das escolas, pois, como ingressantes em 2008, dando oportunidade,
permaneciam na sala durante a atividade, aos mesmos, de colaborarem com sua própria
passaram a repensar melhor sobre sua prática formação.
docente.
Referências
Conclusão
[1] A. M. Boavida, Resolução de problemas:
Ao final de, praticamente, seis meses Que rumos para a educação matemática?
de trabalho, pode-se dizer que o resultado foi em “Educação Matemática - Temas de
maravilhoso, superando as expectativas. Este Investigação” (M. Brown, D. Fernandes, J.
foi um grupo que começou sem nenhuma F. Matos & J. P. Ponte, eds.), pp. 105 -
perspectiva, mas com esperanças que 114, Lisboa: IIE/SPCE, 1992.
pudessem mudar a opinião preconceituosa
sobre a prática de ensino. [2] J. Borin. “Jogos e resolução de
Nesse pouco tempo foi possível problemas: uma estratégia para as aulas de
perceber a grandiosa contribuição que o matemática”, São Paulo: IME-USP,
projeto trouxe a comunidade como um todo. 1996.
Os alunos integrantes do grupo tiveram um
amadurecimento significativo com a atividade [3] J. Piaget. “Estudos Sociológicos”. Rio de
na qual desenvolveram; adquiriram a Janeiro: Forense, 1973.
habilidade da pesquisa, do trabalho em grupo,
[4] M. Guzmán. Tendencias actuales de la
da organização do tempo, do
enseñanza de la matemática, Studia
comprometimento, e mais, o “choque” com a
Paedagogica, Revista de Ciencias de la
realidade fez com que eles pudessem “sentir
Educación, vol.21, pp 19 - 26, (1989).
na pele” o que realmente é a profissão que
escolheram, e o que podem fazer para [5] M. O. Moura. A séria busca no jogo: do
melhorar a situação precária na qual se lúdico na matemática, A Educação
encontra o ensino público. Matemática em Revista, SBEM, n.3,
Essa atividade foi o passo inicial para 1994.
a modificação na estrutura educacional,
visando o ensino de qualidade em todos os [6] R. P. Brenelli, “O jogo como espaço para
níveis; na universidade, permitindo aos alunos pensar: a construção de noções lógicas e
a oportunidade de conhecer de perto a aritméticas”. Campinas, São Paulo:
profissão que escolheram, contribuindo assim Papirus, 1996.
para sua formação; nas escolas de ensino
fundamental e médio, modificando a realidade [7] S. M. P. Santos. “O lúdico na formação
do ensino, principalmente de matemática, do educador”, Petrópolis, Rio de Janeiro:
tornando-o mais atrativo, através da utilização Vozes, 1997.
jogos matemáticos como ferramentas [8] ____Secretaria da Educação Fundamental.
educacionais alternativas; e “Parâmetros Curriculares Nacionais”,
conseqüentemente, modificando a comunidade Brasília: MEC/SEF, pp. 48 - 49, 1997.
como um todo.](https://image.slidesharecdn.com/03relatorio2008-110906153354-phpapp02/85/Relatorio-de-Atividades-2008-25-320.jpg)
![Utilização de Jogos no Ensino de Matemática – Cubo Soma
Gustavo Carvalho Molina
Universidade Estadual Paulista “Julio de Mesquita Filho”
15385-000, Campus de Ilha Solteira, SP
E-mail: gustavo_carvalhomolina@hotmail.com
Alessandra B. Altran, Dalva M. O. Villarreal, Mara L. M. Lopes
Depto de Matemática, FEIS, UNESP
15385-000, Ilha Solteira, SP
E-mail: lealtran@mat.feis.unesp.br, dalva@mat.feis.unesp.br, mara@mat.feis.unesp.br
RESUMO
A utilização de jogos pode constituir um
ferramental auxiliar no ensino e aprendizagem
da matemática. Os jogos matemáticos tornam
o aprendizado mais prazeroso e descontraído,
saindo da rotina maçante de conteúdos em sala
de aula para uma atividade mais prática e
dinâmica. Assim, foi formado um grupo de
alunos para estudar tais jogos, com a
finalidade de levá-los às escolas Figura 2: Formas criadas
proporcionando uma maneira diferente de
ensinar matemática. As atividades com jogos matemáticos contam
com um grupo de 12 alunos do curso de
A intenção central do estudo foi fazer com que Licenciatura em Matemática. Inicialmente
os alunos do ensino Fundamental e Médio fazemos pesquisa aprofundada para
adquirissem alguns conceitos matemáticos que conhecermos cada jogo, em seguida
não ficavam bem esclarecidos em sala de aula procuramos formas de confeccionar os jogos
como, por exemplo, noção de área, volume, e, após várias apresentações para o grupo,
componentes de um sólido geométrico (tais fazemos apresentações nas escolas públicas de
como, aresta, faces, vértices). Também ensino Fundamental e Médio. A partir desse
possibilitar a manipulação de objetos e as trabalho podemos organizar os jogos de
tentativas de encaixamentos para construções maneira a buscar resultados específicos no
usando policubos (peças componentes do aprendizado dos alunos.
Cubo Soma), um cubo maior 3x3x3 unidades.
O trabalho com jogos matemáticos é muito
interessante no que diz respeito à construção
de conhecimento dos alunos, já que os
mesmos ficam mais motivados em relação a
fazer descobertas e pesquisas sobre assuntos
referentes a tais jogos.
Referências
Figura 1: Peças do Cubo Soma.
[1] http://www.espacociencia.pe.gov.br/areas/
Em determinadas séries, os alunos podem matematica/cubo.php
tentar desenhar, criar outras formas com as Acesso em: 22/03/2008.
peças do Cubo Soma, como sofás, poltronas,
mesas, fatos que tornam a atividade com o [2] http://pt.wikipedia.org/wiki/CuboSoma
Cubo Soma ainda mais divertida e Acesso em: 22/03/2008.
desafiadora.](https://image.slidesharecdn.com/03relatorio2008-110906153354-phpapp02/85/Relatorio-de-Atividades-2008-26-320.jpg)
![Utilização de Jogos no Ensino de Matemática – Kakuro
Aline J. Silva, Edcarlos L. F. Santos, Jonatas E. S. Silva
Universidade Estadual Paulista “Julio de Mesquita Filho”
15385-000, Campus de Ilha Solteira, SP
E-mail: aline71142@aluno.feis.unesp.br, edcarlos71125@aluno.feis.unesp.br,
jonatas71179@aluno.feis.unesp.br
Alessandra B. Altran, Dalva M. O. Villarreal, Mara L. M. Lopes
Depto de Matemática, FEIS, UNESP
15385-000, Ilha Solteira, SP
E-mail: lealtran@mat.feis.unesp.br, dalva@mat.feis.unesp.br, mara@mat.feis.unesp.br
RESUMO
O Kakuro foi criado no Japão, porém, sua O objetivo de levar o Kakuro para sala de aula
propagação foi dada nos Estados Unidos e na se baseia no fato de grande parcela dos alunos
Inglaterra na década de 90. O jogo é rejeitarem a disciplina de matemática; e nós,
constituído por uma tabela contendo números como educadores, temos a responsabilidade de
naturais, de um a nove (excluindo assim o criar, inovar e tornar a aula mais dinâmica, a
zero), tendo como objetivo fazer com que a fim de atender aos anseios de nossos alunos. O
soma de cada linha seja igual ao número Kakuro é um passatempo que exige lógica e
mostrado à esquerda, e a soma de cada coluna conhecimento matemático, podendo assim, ser
seja igual ao número mostrado no topo, como levado para dentro da sala de aula. Em [3],
mostra a figura 1. POSSANI afirma que “O jogo Kakuro é um
jogo tipíco para usar em atividades escolares,
pois, une estética, gosto pelo desafio e
conteúdo matemático específico”.
Quando utilizado em sala de aula, o Kakuro
pode ser aplicado em todas as séries, ou seja, é
possível trabalhar com o Kakuro com alunos
de diversas idades, estabelecendo-se o mesmo
objetivo, visando o raciocínio lógico, noções
de soma e combinação de números, porém,
Figura 1. Representação da soma. adaptados de acordo com as séries.
Porém, como mostra a figura 2, os números No projeto de divulgação de Jogos
utilizados não podem ser repetidos tanto nas Matemáticos do Laboratório de Ensino de
linhas, quanto nas colunas, ou seja, numa Matemática da Unesp de Ilha Solteira, várias
mesma linha, ou coluna, não podem ter situações de aplicação de jogos para crianças,
números repetidos. têm sido vivenciadas nas escolas da região.
Referências
[1] http://pt.wikipedia.org/wiki/Kakuro
Acesso em: 22/03/2008.
[2] http://rachacuca.com.br/kakuro
Acesso em: 22/03/2008.
[3] http://revistaepoca.globo.com/Revista/Epo
Figura 2. Representação de repetição não ca/0,,EDR73605-6014,00.html
permitida. Acesso em: 22/03/2008.](https://image.slidesharecdn.com/03relatorio2008-110906153354-phpapp02/85/Relatorio-de-Atividades-2008-27-320.jpg)
![Utilização de Jogos no Ensino de Matemática – Quadrado
Mágico
Tiago Henrique Pereira da Silva
Universidade Estadual Paulista “Julio de Mesquita Filho”
15385-000, Campus de Ilha Solteira, SP
E-mail: tiagohenrique.mat@aluno.feis.unesp.br
Alessandra B. Altran, Dalva M. O. Villarreal, Mara L. M. Lopes
Depto de Matemática, FEIS, UNESP
15385-000, Ilha Solteira, SP
E-mail: lealtran@mat.feis.unesp.br, dalva@mat.feis.unesp.br, mara@mat.feis.unesp.br
RESUMO
Segundo a história da Matemática o Quadrado mais avançadas, fizemos uma introdução ao
Mágico foi descoberto pelos chineses há mais hexágono mágico.
de 3.000 anos antes de Cristo. Conta-se que o
primeiro registro de um quadrado mágico - de A apresentação dos jogos despertou grande
origem antiga, mas desconhecida - foi curiosidade nas crianças, contribuindo para o
supostamente trazido para os homens por uma aprendizado de matemática; sentimos que os
tartaruga do rio Lo, nos dias do lendário professores, mesmo possuindo o
imperador Yii, considerado um engenheiro conhecimento dos jogos, ficam inseguros com
hidráulico. Evidentemente, a forma dos o novo método que acaba tornando a aula mais
algarismos não era igual aos que estão no dinâmica e atrativa, otimizando a
casco da tartaruga, mas os valores, sim. aprendizagem.
O Quadrado Mágico consiste em uma matriz O ensino/aprendizagem de matemática
numérica quadrada, em que, as somas das constitui um grande problema na atual
linhas, das colunas e das duas diagonais situação educacional que enfrentamos. A
principais são as mesmas. Por exemplo, o mudança de postura em sala de aula deve ser
Quadrado Mágico 3 x 3, é formado pelos nove uma das tentativas dos educadores na intenção
dígitos: 1, 2, 3, 4, 5, 6, 7, 8 e 9, dispostos em de despertar o interesse de seus aprendizes
três linhas e três colunas, neste caso, as somas para a beleza do estudo da matemática, ou
nos sentidos horizontais, verticais e diagonais, seja, o educador é a peça chave no processo da
são constantes e iguais a 15. reforma educacional.
Referências
[1] http://pt.wikipedia.org/wiki/Quadrado_má
gico
Acesso em: 22/03/2008.
[2] http://www.jogosboole.com.br/tutoriais_m
Figura 1- Quadrado Mágico ostra.asp?id=19
Acesso em: 22/03/2008.
O Quadrado Mágico foi apresentado em duas
escolas da cidade de lha Solteira e em uma [3] http://galileu.globo.com/edic/92/desafio1.
escola da cidade de Selvíria (MS), através de htm
aulas teórico-expositivas, assim, optamos pela Acesso em: 22/03/2008.
divisão em níveis, já que foram atendidos
alunos de séries diferentes e, para as séries](https://image.slidesharecdn.com/03relatorio2008-110906153354-phpapp02/85/Relatorio-de-Atividades-2008-28-320.jpg)
![Utilização de Jogos no Ensino de Matemática – Sudoku
Deleon M. Alvarenga, Silvio R. Junior, Vinicius A. S. Guissi
Universidade Estadual Paulista “Julio de Mesquita Filho”
15385-000, Campus de Ilha Solteira, SP
E-mail: deleon71070@aluno.feis.unesp.br, silvio71015@aluno.feis.unesp.br, vinnyguissi@hotmail.com
Alessandra B. Altran, Dalva M. O. Villarreal, Mara L. M. Lopes
Depto de Matemática, FEIS, UNESP
15385-000, Ilha Solteira, SP
E-mail: lealtran@mat.feis.unesp.br, dalva@mat.feis.unesp.br, mara@mat.feis.unesp.br
RESUMO
O trabalho enfatiza a utilização de jogos símbolos, formas, cores e letras, que podem
matemáticos, neste caso específico o jogo ser usados sem alterar as regras.
Sudoku, no ensino de matemática. A
utilização de jogos traz um grande estímulo ao Em nosso trabalho, foram atendidas escolas de
aprendizado, pois, além de motivar os alunos, ensino fundamental e médio (públicas e
exigem aumento da concentração e disciplina. particulares), por esse motivo, houve a
necessidade de abordar o Sudoku nas diversas
Suuji wa dokushin ni kagiru, uma grande frase formas e níveis, de acordo com a série na qual
para nomear um jogo matemático, conhecido seria abordado. A intenção foi proporcionar o
como Sudoku; a tradução da frase pode ser aumento do aproveitamento dos alunos dentro
entendida como: os dígitos devem permanecer de sala de aula, estimulando a memória, a
únicos. O jogo Sudoku é constituído por uma manipulação de informações, e o raciocínio
grade 9x9 dividida em sub-grades 3x3, que lógico dos alunos. Outros jogos foram
são chamadas de regiões (ou ainda, caixas, abordados em complementação ao Sudoku,
blocos, quadrantes). Cada local onde se coloca por exemplo, o Kakuro, estimulando também
o número é chamado de célula. Algumas o cálculo aritmético.
células já contêm os chamados “números
dados” que, dependendo da dificuldade, Com a introdução dos jogos matemáticos
variam de quantidade. O objetivo do jogo é percebemos um grande interesse dos alunos
completar todas as células com números de 1 a nessas atividades; quando a matemática
9, de maneira que nenhum número se repita existente em cada jogo foi exposta de maneira
nas linhas, colunas e regiões. Veja a figura a formal, notamos certa curiosidade, e
seguir. disposição dos alunos em entender e vencer o
jogo a eles proposto. Sendo assim, foi possível
diversificar a forma de ensino mostrando aos
professores novas opções de trabalho.
Referências
[1] http://www.abril.com.br/sudoku
Acesso em: 22/03/2008.
[2] www.jjx.com.br/sudoku
Acesso em: 22/03/2008.
Figura 1- Sudoku
[3] www.wikipedia.org/Sudoku
Porém, existem várias formas de Sudoku: o Acesso em: 22/03/2008.
numérico (o mais usado), combinação de](https://image.slidesharecdn.com/03relatorio2008-110906153354-phpapp02/85/Relatorio-de-Atividades-2008-29-320.jpg)

![Utilização de Jogos Matemáticos como Ferramenta Alternativa à
Metodologia Tradicional do Ensino de Matemática
Alessandra B. Altran, Dalva M. O. Villarreal, Mara L. M. Lopes
Depto de Matemática, FEIS, UNESP,
15385-000, Ilha Solteira, SP
E-mails: lealtran@mat.feis.unesp.br, dalva@mat.feis.unesp.br, mara@mat.feis.unesp.br
RESUMO
O objetivo deste trabalho é relatar a Portanto, pode-se dizer tal proposta foi o passo
experiência do uso pedagógico dos jogos inicial para a modificação na estrutura
durante as aulas de Matemática, em escolas de educacional, visando o ensino de qualidade em
ensino fundamental. Por outro lado, trabalho todos os níveis; na universidade, permitindo
ainda tem o propósito de evidenciar a aos alunos a oportunidade de conhecer de
importância da inserção da abordagem dos perto a profissão que escolheram, contribuindo
jogos matemáticos durante processo de assim para sua formação; nas escolas de
formação de educadores, ou seja, comprovar o ensino fundamental e médio, modificando a
valor da utilização dessa ferramenta realidade do ensino, principalmente de
alternativa através da experiência prática matemática, tornando-o mais atrativo, através
adquirida com a atividade na qual está sendo da utilização jogos matemáticos como
formado para desenvolver. ferramentas educacionais alternativas; e
conseqüentemente, modificando a comunidade
Assim, para o desenvolvimento dessa como um todo.
atividade de extensão, foi formado o “Grupo
de Estudo sobre Jogos Matemáticos”, Referências
composto por doze alunos do curso de
Licenciatura em Matemática e três professores [1] A. M. Boavida, Resolução de problemas:
da UNESP de Ilha Solteira, que têm como Que rumos para a educação matemática?
principal objetivo a divulgação da em “Educação Matemática - Temas de
metodologia de utilização de jogos no ensino Investigação” (M. Brown, D. Fernandes,
de matemática, como alternativa à postura J. F. Matos & J. P. Ponte, eds.), pp. 105 -
tradicional do professor. 114, Lisboa: IIE/SPCE, 1992.
O processo de experimentação se deu em duas [2] J. Borin. “Jogos e resolução de
escolas da rede municipal de ensino dos problemas: uma estratégia para as aulas
municípios de Ilha Solteira (SP) e Selvíria de matemática”, São Paulo: IME-USP,
(MS), desse modo, foi possível observar que 1996.
tal atividade provocou certo contentamento [3] J. Piaget. “Estudos Sociológicos”. Rio de
por parte dos alunos e uma modificação na Janeiro: Forense, 1973.
forma de pensar dos próprios professores das
escolas. [4] M. Guzmán. Tendencias Actuales de la
Enseñanza de la Matemática, Studia
Em relação aos alunos integrantes do grupo, Paedagogica, Revista de Ciencias de la
pode-se dizer que os mesmos tiveram um Educación, vol.21, pp 19 - 26, (1989).
amadurecimento significativo com a atividade [5] M. O. Moura. A séria busca no jogo: do
na qual desenvolveram; adquiriram a lúdico na matemática, A Educação
habilidade da pesquisa, do trabalho em grupo, Matemática em Revista, SBEM, n.3,
do comprometimento, e mais, o “choque” com 1994.
a realidade fez com que eles pudessem “sentir
na pele” o que realmente é a profissão que [6] ____Secretaria da Educação
escolheram, e o que podem fazer para Fundamental. “Parâmetros Curriculares
melhorar a situação precária na qual se Nacionais”, Brasília: MEC/SEF, pp. 46 -
encontra o ensino público. 47, 1998.](https://image.slidesharecdn.com/03relatorio2008-110906153354-phpapp02/85/Relatorio-de-Atividades-2008-31-320.jpg)
![O uso do jogo Cubo Soma como instrumento auxiliar no
ensino de Matemática
Gustavo Carvalho Molina
Universidade Estadual Paulista “Julio de Mesquita Filho”
15385-000, Campus de Ilha Solteira, SP
E-mail: gustavo_carvalhomolina@hotmail.com
Alessandra B. Altran, Dalva M. O. Villarreal, Mara L. M. Lopes
Depto de Matemática, FEIS, UNESP
15385-000, Ilha Solteira, SP
E-mail: lealtran@mat.feis.unesp.br, dalva@mat.feis.unesp.br, mara@mat.feis.unesp.br
RESUMO
Na tentativa de fazer do ensino de matemática
uma atividade prazerosa, apostou-se na
utilização de ferramentas alternativas, tais
como, os jogos matemáticos. A utilização dos
jogos em sala de aula propicia um maior
aprendizado saindo da rotina maçante de
conteúdos para uma atividade mais prática e Figura 2: Formas criadas com os Policubos.
dinâmica. Deste modo, o objetivo da análise
do jogo Cubo Soma, foi buscar uma O trabalho foi iniciado com a pesquisa
ferramenta que possibilitasse a aquisição, por aprofundada do jogo, destacando notação
parte dos alunos do ensino Fundamental e histórica, fundamentação matemática,
Médio, de conceitos matemáticos que não contribuição pedagógica, e ainda, a confecção
ficavam bem esclarecidos em sala de aula do Cubo Soma. Após várias apresentações
como, por exemplo, noção de área, volume, para o próprio grupo, foram feitas
componentes de um sólido geométrico (tais apresentações nas escolas públicas de ensino
como, aresta, faces, vértices). Fundamental e Médio.
O cubo soma é um quebra-cabeça criado em Portanto, foi possível observar a contribuição
1936 pelo poeta e matemático dinamarquês que esse tipo de atividade proporciona,
Piet Hein. O objetivo é usar os sete policubos principalmente, no que diz respeito à
(peças formadas por pequenos cubos unitários) construção de conhecimento dos alunos, já que
para montar um cubo de 3x3x3 unidades. os mesmos ficam mais motivados em relação a
Existem 240 maneiras distintas de montar o fazer descobertas e pesquisas sobre assuntos
cubo soma, sem contar rotações e reflexões. referentes a tais jogos.
Referências
[1] A. H. Ferrari, M. C. C. S. Carvalho e P.
Furtado,“Conhecendo o Cubo Soma”,
Anais do X Simpósio Multidisciplinar da
Figura 1: Os Policubos e o Cubo Soma. USJT, 2004.
As peças também podem ser usadas para [2] http://www.espacociencia.pe.gov.br/areas/
montar uma variedade de formas matematica/cubo.php
tridimensionais interessantes, como poltronas, Acesso em: 29/04/2008.
mesas e cadeiras, fatos que tornam a atividade
com o Cubo Soma ainda mais divertida e [3] http://pt.wikipedia.org/wiki/CuboSoma
desafiadora. Acesso em: 29/04/2008.](https://image.slidesharecdn.com/03relatorio2008-110906153354-phpapp02/85/Relatorio-de-Atividades-2008-32-320.jpg)
![A utilização do jogo Kakuro no ensino de Matemática
Aline J. Silva, Edcarlos L. F. Santos, Jonatas E. S. Silva
Universidade Estadual Paulista “Julio de Mesquita Filho”
15385-000, Campus de Ilha Solteira, SP
E-mail: aline71142@aluno.feis.unesp.br, edcarlos71125@aluno.feis.unesp.br,
jonatas71179@aluno.feis.unesp.br
Alessandra B. Altran, Dalva M. O. Villarreal, Mara L. M. Lopes
Depto de Matemática, FEIS, UNESP
15385-000, Ilha Solteira, SP
E-mail: lealtran@mat.feis.unesp.br, dalva@mat.feis.unesp.br, mara@mat.feis.unesp.br
RESUMO
A utilização de jogos no ensino de matemática O Kakuro é um passatempo que exige lógica e
é uma prática freqüente nas escolas municipais conhecimento matemático podendo, assim, ser
de ensino infantil e fundamental do município levado para dentro da sala de aula. Como
de Ilha Solteira, resultado de uma atividade grande parte dos alunos rejeita a disciplina da
intensa de pesquisa e experimentação do matemática, optou-se por utilizar o jogo
grupo de estudo formado por alunos do curso Kakuro de modo a tornar a aula mais
de Licenciatura em Matemática da UNESP de dinâmica, a fim de atender aos anseios dos
Ilha Solteira. alunos. Em [3], POSSANI afirma que “O jogo
Kakuro é um jogo tipíco para usar em
Um dos jogos abordados é o Kakuro. O atividades escolares, pois, une estética, gosto
Kakuro, criado no Japão, é um jogo pelo desafio e conteúdo matemático
constituído por uma tabela contendo números específico”.
naturais, de um a nove (excluindo assim o
zero), cujo objetivo é fazer com que a soma de Na escola, a abordagem do Kakuro pode
cada linha seja igual ao número mostrado à ocorrer em todas as séries, ou seja, o Kakuro
esquerda, e a soma de cada coluna seja igual pode ser trabalhado com alunos de diversas
ao número mostrado no topo. idades, estabelecendo-se o mesmo objetivo,
visando o raciocínio lógico, noções de soma e
combinação de números, porém, adaptados de
acordo com as séries. No projeto de
divulgação de Jogos Matemáticos do
Laboratório de Ensino de Matemática da
UNESP de Ilha Solteira, várias situações de
aplicação de jogos para crianças, têm sido
vivenciadas nas escolas da região.
Figura 1. Representação da soma.
Porém, numa mesma linha, ou coluna, não Referências
pode haver números repetidos.
[1] http://www.kakuro.com/howtoplay.php
Acesso em: 29/04/2008.
[2] http://rachacuca.com.br/kakuro
Acesso em: 29/04/2008.
[3] http://revistaepoca.globo.com/Revista/Epo
ca/0,,EDR73605-6014,00.html
Acesso em: 29/04/2008.
Figura 2. Representação de repetição não [4] http://pt.wikipedia.org/wiki/Kakuro
permitida. Acesso em: 29/04/2008.](https://image.slidesharecdn.com/03relatorio2008-110906153354-phpapp02/85/Relatorio-de-Atividades-2008-33-320.jpg)
![O ensino de Matemática através do uso do jogo Sudoku
Deleon M. Alvarenga, Silvio R. Junior, Vinicius A. S. Guissi
Universidade Estadual Paulista “Julio de Mesquita Filho”
15385-000, Campus de Ilha Solteira, SP
E-mail: deleon71070@aluno.feis.unesp.br, silvio71015@aluno.feis.unesp.br, vinnyguissi@hotmail.com
Alessandra B. Altran, Dalva M. O. Villarreal, Mara L. M. Lopes
Depto de Matemática, FEIS, UNESP
15385-000, Ilha Solteira, SP
E-mail: lealtran@mat.feis.unesp.br, dalva@mat.feis.unesp.br, mara@mat.feis.unesp.br
RESUMO
A utilização de jogos matemáticos no ensino
proporciona um grande estímulo ao
aprendizado, pois, além de motivar os alunos,
exigem aumento da concentração e disciplina.
Dessa forma, um grupo estudos sobre jogos
matemáticos, composto por alunos do curso de Figura 2- Variações do Sudoku
Licenciatura em Matemática da Unesp de Ilha
Solteira, foi formado a fim estudar toda a Como são atendidas escolas de ensino
teoria sobre jogos, possibilitando levá-lo para fundamental e médio, ocorre à necessidade de
a sala de aula. Logo, esse trabalho mostra a abordar o Sudoku nas diversas formas e
utilização do jogo Sudoku, no ensino de níveis, de acordo com a série na qual é
matemática. abordado. O objetivo maior é proporcionar o
aumento do aproveitamento dos alunos dentro
O jogo Sudoku é constituído por uma grade de sala de aula, estimulando a memória, a
9x9 dividida em sub-grades 3x3, que são manipulação de informações, e o raciocínio
chamadas de regiões (ou ainda, caixas, blocos, lógico dos alunos.
quadrantes). Cada local onde se coloca o
número é chamado de célula. Algumas células
Portanto, com a introdução dos jogos
já contêm os chamados “números dados” que,
matemáticos foi possível perceber o grande
dependendo da dificuldade, variam de
interesse dos alunos nessas atividades; quando
quantidade. O objetivo do jogo é completar
a matemática existente em cada jogo foi
todas as células com números de 1 a 9, de
exposta de maneira formal, notou-se certa
maneira que nenhum número se repita nas
curiosidade e disposição dos alunos em
linhas, colunas e regiões.
entender e vencer o jogo a eles proposto.
Sendo assim, foi possível diversificar a forma
de ensino mostrando aos professores novas
opções de trabalho.
Referências
[1] T. Davis, “The Mathematics of Sudoku”,
http://www.geometer.org/mathcircles,
2007.
Figura 1- Sudoku
[2] www.jjx.com.br/sudoku
Porém, existem várias formas de Sudoku: o Acesso em: 29/04/2008.
numérico (o mais usado), combinação de
símbolos, formas, cores e letras, que podem [3] www.wikipedia.org/Sudoku
ser usados sem alterar as regras. Acesso em: 29/04/2008.](https://image.slidesharecdn.com/03relatorio2008-110906153354-phpapp02/85/Relatorio-de-Atividades-2008-34-320.jpg)












![SILVA, A. J., SILVA, J. E. S., ALTRAN, A. B., VILLARREAL, D. M. O. e LOPES,
M. L. M. O kakuro como uma Ferramenta no Aprendizado de Matemática, Relato de
Experiência. Anais do IX Encontro Paulista de Educação Matemática: IX EPEM.
Bauru: SBEM/SBEM-SP, 2008, pp. 1-8. (ISBN 978-85-98092-07-2)
Eixo-temático: Ensino Fundamental: Ciclos III e IV
O KAKURO COMO UMA FERRAMENTA NO APRENDIZADO DE
MATEMÁTICA
Aline J. SILVA – FEIS / UNESP (aline71142@aluno.feis.unes.br)
Jonatas E. S. da SILVA – FEIS / UNESP (jonatas71179@aluno.feis.unes.br)
Alessandra B. ALTRAN – FEIS / UNESP (lealtran@mat.feis.unesp.br)
Dalva M. O. VILLARREAL – FEIS / UNESP (dalva@mat.feis.unesp.br)
Mara L. M. LOPES – FEIS / UNESP (mara@mat.feis.unesp.br)
Resumo: Devido o prazer propiciado e o desafio alucinante, o gosto por jogos torna o
homem um verdadeiro “jogador”, o chamado “Homo Ludens”. Nos dias atuais o
homem joga constantemente e pode-se dizer que o próprio ato de viver torna-se um
“jogo”, pois, em diversas fases da vida sucede-se o fato de estar enfrentando um jogo no
qual, automaticamente, estão subentendido as suas regras onde os mais fortes e
preparados possuem a chance de se sobressair. São vários os exemplos de ambientes
onde ocorre a inserção dos jogos, é possível perceber que eles também foram se
intensificando dentro de sala de aula. O uso alternativo dos jogos lúdicos favorece ao
aluno uma aprendizagem de fácil assimilação, ou seja, o aluno tem a possibilidade de
aprender o conteúdo de uma forma mais simples e agradável. O jogo Kakuro teve sua
criação no Japão, todavia sua propagação se deu nos Estados Unidos da América e na
Inglaterra, na década de 90, sendo assim conhecido na língua inglesa por Cross Sums
que significa “Somas Cruzadas”. O objetivo deste trabalho é analisar e apresentar o jogo
Kakuro com a possibilidade de sua inserção dentro de sala de aula. O estudo aqui
apresentado focaliza a forma lúdica do aprendizado que foi proporcionado pelo jogo
Kakuro, apesar de não internalizado nos âmbitos profissionais, mas com fortes
expectativas a partir da experiência formativa. Jogar o Kakuro é embarcar em um
desafio repleto de obstáculos fabulosos que propiciará ao jogador uma verdadeira
ginástica cerebral. O Kakuro, além de exercitar a mente através do raciocínio lógico,
tem a finalidade de estimular o gosto pela Matemática e consolidar o aprendizado das
quatro operações aritméticas. POSSANI [LEAL, 2006] afirma que “O jogo Kakuro é
um jogo típico para usar em atividades escolares, pois, une estética, gosto pelo desafio
e conteúdo matemático específico”.
Palavras-chave: Kakuro, Jogos Lúdicos, Raciocínio Lógico, Aprendizagem
Matemática.](https://image.slidesharecdn.com/03relatorio2008-110906153354-phpapp02/85/Relatorio-de-Atividades-2008-47-320.jpg)




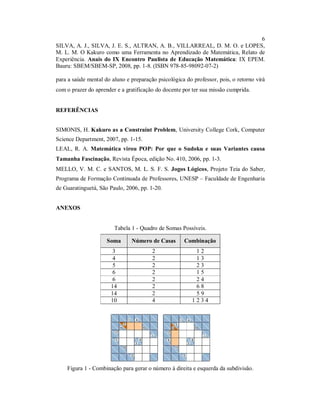
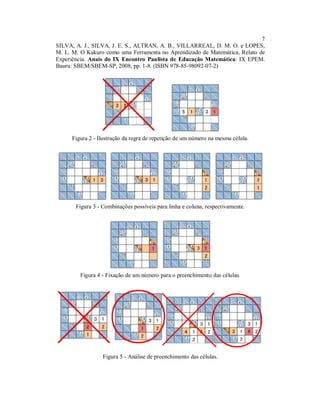



















![3
NIZA, C. D., BEVILAQUA, N. M., ALTRAN, A. B., VILLARREAL, D. M. O. e
LOPES, M. L. M. O Tangram como Ferramenta Complementar ao Ensino de
Matemática, Relato de Experiência. Anais do IX Encontro Paulista de Educação
Matemática: IX EPEM. Bauru: SBEM/SBEM-SP, 2008, pp. 1-12. (ISBN 978-85-
98092-07-2)
LENDAS E ORIGEM DO TANGRAM
A primeira publicação sobre a origem do Tangram foi em 1813 [LEE, 2003],
segundo os registros.
Várias lendas contam essa origem de formas diferentes, porém, a definição mais
formal diz que o Tangram é um quebra-cabeça de origem chinesa formado por sete
peças (Figura 1), e quando colocadas corretamente, forma-se um quadrado. A essas sete
peças dá-se o nome de Tans e é possível montar cerca de 1700 figuras com as mesmas
(Figura 2) [KALEFF et al., 2002].
REGRAS E MANIPULAÇÃO DO JOGO
O desafio dos quebra-cabeças é recompor estas formas mudando as sete peças de
posições. As duas principais e únicas regras são: usar todas as peças e não sobrepor uma
sobre a outra. Na matemática pode-se introduzir a geometria de maneira mais adequada
através de exposição de sólidos geométricos e da construção do Tangram, para que o
aluno venha a ter noção de espaço, comparar e mediar área, estudar amplitudes de
ângulos e comprimento.
Uma maneira interessante de jogar este jogo é colocar os dois jogadores sentados
frente a frente, onde o primeiro escolhe uma figura simples, dando, ou não, um nome a
mesma. O segundo jogador não vê a figura e deve, com as peças do quadrado, construí-
la segundo as indicações do primeiro jogador, que lhe descreve as peças e as respectivas
posições. O segundo jogador só conseguirá reconstruir a figura, se as informações do
primeiro jogador forem suficientemente claras. Pode-se continuar até que o segundo
jogador consiga terminar o jogo, ou então, limitar-se o tempo.
VARIAÇÕES DO TANGRAM
A partir do Tangram clássico surgiram vários outros tipos de Tangram, entre eles,
o Tangram Pitagórico (Figura 3), através da construção feita pode-se concluir que, num](https://image.slidesharecdn.com/03relatorio2008-110906153354-phpapp02/85/Relatorio-de-Atividades-2008-73-320.jpg)
![4
NIZA, C. D., BEVILAQUA, N. M., ALTRAN, A. B., VILLARREAL, D. M. O. e
LOPES, M. L. M. O Tangram como Ferramenta Complementar ao Ensino de
Matemática, Relato de Experiência. Anais do IX Encontro Paulista de Educação
Matemática: IX EPEM. Bauru: SBEM/SBEM-SP, 2008, pp. 1-12. (ISBN 978-85-
98092-07-2)
triangulo retângulo a área do quadrado construído sobre a hipotenusa é igual à soma das
áreas dos quadrados construídos sobre os catetos. Foi assim que Pitágoras chegou a
conclusão de que: a² = b² + c². Conta a lenda que, como prova de gratidão por ter
demonstrado esse teorema, Pitágoras sacrificou 100 bois aos deuses.
Com o passar do tempo foram surgindo vários outros modelos de Tangram, como
Pentagonal, Cardiotangram, Oval, Retangular, Circular, Russo, Triangular, Quatro
peças e Cinco peças (Figura 3).
CONTRIBUIÇÕES PEDAGÓGICAS
O fato de mexer com a imaginação fazem do Tangram um excelente jogo infantil
e educacional, especialmente se for possível permitir à criança a criação do seu próprio
jogo. Com o uso do Tangram o professor pode desenvolver, ou aperfeiçoar, com seus
alunos, várias capacidades, como identificação de formas geométricas planas, através de
cores, formas, comparação, descrição, classificação, transformações geométricas através
de composição e decomposição de figuras, compreensão das propriedades das figuras
geométricas planas, representação e resolução de problemas usando modelos
geométricos, noções de área e frações. O Tangram também possibilita obter algumas
habilidades importantes para a aquisição de conhecimento em outras áreas, tais como,
visualização, diferenciação, percepção espacial, análise, síntese, desenho, escrita e
construção [LEE, 2003].
O Tangram pode ser usado como material didático nas aulas de educação artística
e matemática, visando à exploração das peças e identificação de suas formas,
possivelmente, com a associação de cores. Logo depois, se passa à sobreposição e
construção de figuras dadas, nesse caso, cabe ao aluno reconhecer e interpretar o que se
pede, analisar as possibilidades e tentar a construção. Durante todo esse processo, a
criança precisa analisar as propriedades das peças do Tangram e da figura que se quer
construir, se detendo ora no todo de cada figura, ora nas partes. Sua filosofia é de que](https://image.slidesharecdn.com/03relatorio2008-110906153354-phpapp02/85/Relatorio-de-Atividades-2008-74-320.jpg)

![6
NIZA, C. D., BEVILAQUA, N. M., ALTRAN, A. B., VILLARREAL, D. M. O. e
LOPES, M. L. M. O Tangram como Ferramenta Complementar ao Ensino de
Matemática, Relato de Experiência. Anais do IX Encontro Paulista de Educação
Matemática: IX EPEM. Bauru: SBEM/SBEM-SP, 2008, pp. 1-12. (ISBN 978-85-
98092-07-2)
novamente os jogos, incluindo o Tangram e suas variações no “Venha nos Conhecer”,
evento já descrito anteriormente (Figura 4).
RESULTADOS
O Tangram não possui uma única “solução”, são inúmeras soluções e figuras que
podem ser formadas, no que, residiria um grande atrativo. Sendo assim, o quebra-cabeça
chinês permite criar e montar mais de 1.700 figuras entre animais, plantas, pessoas,
objetos, letras, números. O Tangram é uma metodologia de ensino de matemática para
jovens e adultos com ou sem alfabetização. O jogo, que torna divertida a matemática
recreativa, pode tomar vários aspectos: um quebra-cabeça a ser resolvido, um jogo de
competição, uma mágica, paradoxo, falácia ou, simplesmente, Matemática com um
toque qualquer de curiosidade ou diversão.
Foi possível transmitir, através das atividades desenvolvidas, que o Tangram,
além de um jogo divertido, pode ser visto como um material educativo, permitindo ao
professor trabalhar com o mesmo em sala de aula, e aos alunos o entendimento de
vários conceitos, tais como, ângulos, área, perímetro, noções espaciais, associação de
formas e cores, comparação, descrição, comparação, etc. [TOLEDO e TOLEDO, 1997].
Assim, a apresentação do Tangram como instrumento alternativo à prática
educacional, despertou grande interesse tanto pelos alunos quando pelos próprios
professores que participaram das atividades desenvolvidas.
REFERÊNCIAS
LEE, R. Tangram, Editora Isis, LTDA, 2003.
KALEFF, A. M.; MONTEIRO REI, D.; GARCIA, S. S. Quebra-cabeças Geométricos
e formas planas, Editora da Universidade Federal Fluminense - Niterói/RJ, 2002.
TOLEDO, M.; TOLEDO, M. Didática da Matemática: como dois e dois: a
construção da matemática, São Paulo: FTD, 1997.](https://image.slidesharecdn.com/03relatorio2008-110906153354-phpapp02/85/Relatorio-de-Atividades-2008-76-320.jpg)

































![Figura 3 - Resolução da Torre, passo 2.
• Em seguida, com 1 (um) movimento transfere-se o k-ésimo disco para a outra haste vazia
como ilustra a Figura 4.
Figura 4 - Resolução da Torre, passo 1.
• Finalmente, move-se a “sub-torre”, com k-1 discos, para a haste onde se encontra o k-ésimo
disco, como mostra a Figura 5.
Figura 5 - Resolução da Torre, passo 1.
• Utilizando para isso M(k-1) movimentos, ou seja:
M(k) = 2 x M (k-1) + 1
• Obtêm-se assim, uma relação que para cada número k de discos, expressa o número mínimo
de movimentos M(k), baseado no número mínimo de movimentos utilizados para transferir
k-1 discos.
Mas esta fórmula não é facilmente manipulável para um número muito grande de discos,
para isso, é necessária uma fórmula que não dependa do número de movimentos anteriores. Sendo
M(n) o número mínimo de movimentos necessários pra transferir n discos de uma haste para a
outra, tem-se que M(n) é “quase” 2 x M(n-1).
Seja:
A(n) = M(n) + 1, e A(n) = 2 x A (n-1)
Então:
A(n) = 2 x A(n-1) = 2 x [2 x A(n-2)] = 2² x A(n-2) = 2² x 2 x A(n-3) = 2³ x A(n-3) = ... = 2n-1 x A(1)
Como A(1) = M(1) + 1, então, A (1) = 1 + 1 = 2.
Assim:
A(n) = 2n-1 x 2 => A(n) = 2n
E, como:](https://image.slidesharecdn.com/03relatorio2008-110906153354-phpapp02/85/Relatorio-de-Atividades-2008-110-320.jpg)





