1) O documento discute matrizes, vetores e geometria analítica, incluindo operações com matrizes, sistemas lineares, inversão de matrizes e determinantes. 2) Também aborda vetores no plano e no espaço, incluindo produtos escalares, vetoriais e mistos, além de equações de retas e planos. 3) Por fim, examina ângulos e distâncias entre retas e planos, assim como suas posições relativas.

1. MATRIZES, VETORES E
´
GEOMETRIA ANALITICA
Reginaldo J. Santos
Departamento de Matem´ tica-ICEx
a
Universidade Federal de Minas Gerais
http://www.mat.ufmg.br/~regi
Marco 2012
¸

2. Matrizes, Vetores e Geometria Anal´tica
ı
Copyright c 2012 by Reginaldo de Jesus Santos (120228)
´ ¸˜ ¸˜ ¸˜
E proibida a reproducao desta publicacao, ou parte dela, por qualquer meio, sem a pr´ via autorizacao, por
e
escrito, do autor.
¸˜ ¸˜
Editor, Coordenador de Revis˜ o, Supervisor de Producao, Capa e Ilustracoes:
a
Reginaldo J. Santos
ISBN 85-7470-014-2
Ficha Catalogr´ fica
a
Santos, Reginaldo J.
S237m Matrizes, Vetores e Geometria Anal´tica / Reginaldo J. Santos - Belo
ı
Horizonte: Imprensa Universit´ ria da UFMG, 2012.
a
1. Geometria Anal´tica
ı I. T´tulo
ı
CDD: 516.3

3. Sum´ rio
a
´
Prefacio vii
1 Matrizes e Sistemas Lineares 1
1.1 Matrizes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
¸˜
1.1.1 Operacoes com Matrizes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
´
1.1.2 Propriedades da Algebra Matricial . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
¸˜
1.1.3 Aplicacao: Cadeias de Markov . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
¸˜
Apˆ ndice I: Notacao de Somat´ rio . . . . . . . . . .
e o . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
¸˜
1.2 Sistemas de Equacoes Lineares . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
1.2.1 M´ todo de Gauss-Jordan . . . . . . . . . .
e . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
1.2.2 Matrizes Equivalentes por Linhas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43
1.2.3 Sistemas Lineares Homogˆ neos . . . . . . .
e . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45
1.2.4 Matrizes Elementares (opcional) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 49
Apˆ ndice II: Unicidade da Forma Escalonada Reduzida
e . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 64
iii

4. iv Sum´ rio
a
˜
2 Inversao de Matrizes e Determinantes 68
2.1 Matriz Inversa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68
2.1.1 Propriedades da Inversa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 70
2.1.2 Matrizes Elementares e Invers˜ o (opcional) . . .
a . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73
2.1.3 M´ todo para Invers˜ o de Matrizes . . . . . . . .
e a . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 77
¸˜ ¸˜
2.1.4 Aplicacao: Interpolacao Polinomial . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86
¸˜
2.1.5 Aplicacao: Criptografia . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 88
2.2 Determinantes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 95
2.2.1 Propriedades do Determinante . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 100
2.2.2 Matrizes Elementares e o Determinante (opcional) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 112
2.2.3 Matriz Adjunta e Invers˜ o (opcional) . . . . . . .
a . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 115
¸˜
Apˆ ndice III: Demonstracao do Teorema 2.11 . . . . . . .
e . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 127
3 Vetores no Plano e no Espaco ¸ 132
¸˜
3.1 Soma de Vetores e Multiplicacao por Escalar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 134
3.2 Produtos de Vetores . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 161
3.2.1 Norma e Produto Escalar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 161
¸˜
3.2.2 Projecao Ortogonal . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 172
3.2.3 Produto Vetorial . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 175
3.2.4 Produto Misto . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 186
¸˜
Apˆ ndice IV: Demonstracao do item (e) do Teorema 3.5
e . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 201
4 Retas e Planos 204
¸˜
4.1 Equacoes de Retas e Planos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 204
¸˜
4.1.1 Equacoes do Plano . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 204
¸˜
4.1.2 Equacoes da Reta . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 222
ˆ
4.2 Angulos e Distˆ ncias . . . . . . . . .
a . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 248
ˆ
4.2.1 Angulos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 248
4.2.2 Distˆ ncias . . . . . . . . . .
a . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 255
¸˜
4.3 Posicoes Relativas de Retas e Planos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 275
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

5. Sum´ rio
a v
¸˜ ˆ
5 Secoes Conicas 286
5.1 Cˆ nicas N˜ o Degeneradas . . . . . . . . . . .
o a . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 287
5.1.1 Elipse . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 287
5.1.2 Hip´ rbole . . . . . . . . . . . . . . .
e . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 295
5.1.3 Par´ bola . . . . . . . . . . . . . . .
a . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 303
¸˜
5.1.4 Caracterizacao das Cˆ nicas . . . . . .
o . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 310
¸˜
5.2 Coordenadas Polares e Equacoes Param´ tricas
e . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 319
5.2.1 Cˆ nicas em Coordenadas Polares . . .
o . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 325
5.2.2 Circunferˆ ncia em Coordenadas Polares
e . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 332
5.2.3 Equaco¸ ˜ es Param´ tricas . . . . . . . .
e . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 337
6 Superf´cies e Curvas no Espaco
ı ¸ 359
6.1 Qu´ dricas . . . . . . . . . . . . . . . . . . . . . . . . . .
a . . . . . . . . . . . . . . . . . . . . . . . . . . . 359
6.1.1 Elipsoide . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 362
6.1.2 Hiperboloide . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 365
6.1.3 Paraboloide . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 376
6.1.4 Cone El´ptico . . . . . . . . . . . . . . . . . . . .
ı . . . . . . . . . . . . . . . . . . . . . . . . . . . 387
6.1.5 Cilindro Qu´ drico . . . . . . . . . . . . . . . . . .
a . . . . . . . . . . . . . . . . . . . . . . . . . . . 390
ı o ¸˜
6.2 Superf´cies Cil´ndricas, Cˆ nicas e de Revolucao . . . . . . .
ı . . . . . . . . . . . . . . . . . . . . . . . . . . . 400
6.2.1 Superf´cies Cil´ndricas . . . . . . . . . . . . . . . .
ı ı . . . . . . . . . . . . . . . . . . . . . . . . . . . 400
6.2.2 Superf´cies Cˆ nicas . . . . . . . . . . . . . . . . .
ı o . . . . . . . . . . . . . . . . . . . . . . . . . . . 406
ı ¸˜
6.2.3 Superf´cies de Revolucao . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 412
e ¸˜
6.3 Coordenadas Cil´ndricas, Esf´ ricas e Equacoes Param´ tricas
ı e . . . . . . . . . . . . . . . . . . . . . . . . . . . 427
6.3.1 Coordenadas Cil´ndricas . . . . . . . . . . . . . . .
ı . . . . . . . . . . . . . . . . . . . . . . . . . . . 427
6.3.2 Coordenadas Esf´ ricas . . . . . . . . . . . . . . .
e . . . . . . . . . . . . . . . . . . . . . . . . . . . 434
¸˜
6.3.3 Equacoes Param´ tricas de Superf´cies . . . . . . .
e ı . . . . . . . . . . . . . . . . . . . . . . . . . . . 439
¸˜
6.3.4 Equacoes Param´ tricas de Curvas no Espaco . . . .
e ¸ . . . . . . . . . . . . . . . . . . . . . . . . . . . 446
7 Mudanca de Coordenadas
¸ 452
¸˜ ¸˜
7.1 Rotacao e Translacao . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 452
¸˜
7.1.1 Rotacao . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 458
Marco 2012
¸ Reginaldo J. Santos

6. vi Sum´ rio
a
¸˜
7.1.2 Translacao . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 459
7.2 ¸˜
Identificacao de Cˆ nicas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 463
o
7.3 ¸˜
Identificacao de Qu´ dricas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 482
a
Respostas dos Exerc´cios
ı 509
Bibliografia 649
´ndice Alfabetico
I ´ 652
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

7. Pref´ cio
a
Este texto cobre o material para um curso de Geometria Anal´tica ministrado para estudantes da area de
ı ´
Ciˆ ncias Exatas. O texto pode, mas n˜ o e necess´ rio, ser acompanhado um programa como o M ATLAB ∗ ,
e a ´ a
SciLab ou o Maxima.
´ ´
O conteudo e dividido em sete cap´tulos. O Cap´tulo 1 trata das matrizes e sistemas lineares. Aqui todas as
ı ı
´ ¸˜ ´
propriedades da algebra matricial s˜ o demonstradas. A resolucao de sistemas lineares e feita usando somente
a
o m´ todo de Gauss-Jordan (transformando a matriz at´ que ela esteja na forma escalonada reduzida). Este
e e
m´ todo requer mais trabalho do que o m´ todo de Gauss (transformando a matriz, apenas, at´ que ela esteja
e e e
e ´
na forma escalonada). Ele foi o escolhido, por que tamb´ m e usado no estudo da invers˜ o de matrizes no
a
´ ´
Cap´tulo 2. Neste Cap´tulo e tamb´ m estudado o determinante, que e definido usando cofatores. As subsecoes
ı ı e ¸˜
a ¸˜
2.2.2 e 2.2.3 s˜ o independentes entre si. As demonstracoes dos resultados deste cap´tulo podem ser, a crit´ rio
ı e
do leitor, feitas somente para matrizes 3 × 3.
O Cap´tulo 3 trata de vetores no plano e no espaco. Os vetores s˜ o definidos de forma geom´ trica, assim
ı ¸ a e
¸˜
como a soma e a multiplicacao por escalar. S˜ o provadas algumas propriedades geometricamente. Depois s˜ o
a a
¸˜
introduzidos sistemas de coordenadas de forma natural sem a necessidade da definicao de base. Os produtos
escalar e vetorial s˜ o definidos geometricamente. O Cap´tulo 4 trata de retas e planos no espaco. S˜ o estudados
a ı ¸ a
∗ M ATLAB ´
e marca registrada de The Mathworks, Inc.
vii

8. viii Sum´ rio
a
ˆ ¸˜
angulos, distˆ ncias e posicoes relativas de retas e planos.
a
ı ¸˜ ˆ
O Cap´tulo 5 traz um estudo das secoes conicas. S˜ o tamb´ m estudadas as coordenadas polares e
a e
¸˜ ˆ
parametrizacoes das conicas. As superf´cies s˜ o estudadas no Cap´tulo 6 incluindo a´ as qu´ dricas, superf´cies
ı a ı ı a ı
ˆ ¸˜
cil´ndricas, conicas e de revolucao. Neste Cap´tulo s˜ o tamb´ m estudadas as coordenadas cil´ndricas, esf´ ricas
ı ı a e ı e
¸˜
e parametrizacao de superf´cies e curvas no espaco. O Cap´tulo 7 traz mudanca de coordenadas, rotacao e
ı ¸ ı ¸ ¸˜
translacao. Dada uma equacao geral de 2o grau em duas ou trˆ s vari´ veis, neste Cap´tulo, atrav´ s de mudancas
¸˜ ¸˜ e a ı e ¸
´ ¸˜ ˆ
de coordenadas e feita a identificacao da conica ou da qu´ drica correspondente a equacao.
a ¸˜
Os exerc´cios est˜ o agrupados em trˆ s classes. Os “Exerc´cios Num´ ricos”, que cont´ m exerc´cios que s˜ o
ı a e ı e e ı a
resolvidos fazendo c´ lculos, que podem ser realizados sem a ajuda de um computador ou de uma m´ quina
a a
ı ´
de calcular. Os “Exerc´cios Teoricos”, que cont´ m exerc´cios que requerem demonstracoes. Alguns s˜ o sim-
e ı ¸˜ a
ples, outros s˜ o mais complexos. Os mais dif´ceis complementam a teoria e geralmente s˜ o acompanhados
a ı a
˜
de sugestoes. Os “Exerc´cios usando o M ATLAB ”, que cont´ m exerc´cios para serem resolvidos usando o
ı e ı
¸˜
M ATLAB ou outro software. Os comandos necess´ rios a resolucao destes exerc´cios s˜ o tamb´ m forneci-
a ı a e
¸˜ a
dos juntamente com uma explicacao r´ pida do uso. Os exerc´cios num´ ricos s˜ o imprescind´veis, enquanto a
ı e a ı
¸˜
resolucao dos outros, depende do n´vel e dos objetivos pretendidos para o curso.
ı
´
O M ATLAB e um software destinado a fazer c´ lculos com matrizes (M ATLAB = MATrix LABoratory).
a
´
Os comandos do M ATLAB s˜ o muito proximos da forma como escrevemos expressoes alg´ bricas, tornando
a ˜ e
`
mais simples o seu uso. Podem ser incorporados as rotinas pr´ -definidas, pacotes para c´ lculos espec´ficos.
e a ı
¸˜
Um pacote chamado gaal com funcoes que s˜ o direcionadas para o estudo de Geometria Anal´tica e Algebra
a ı ´
Linear pode ser obtido atrav´ s da internet no endereco http://www.mat.ufmg.br/~regi, assim como um
e ¸
¸˜ ¸˜
texto com uma introducao ao M ATLAB e instrucoes de como instalar o pacote gaal. O M ATLAB n˜ o e a ´
um software gratuito, embora antes a vers˜ o estudante vinha gr´ tis ao se comprar o guia do usu´ rio. Atu-
a a a
´ ´
almente o SciLab e uma alternativa gratuita, mas que n˜ o faz c´ lculo simbolico. O Maxima e um programa
a a ´
¸˜
de computacao alg´ brica gratuito. Ambos podem ser usados como ferramenta auxiliar na aprendizagem de
e
´
Geometria Anal´tica e Algebra Linear. Na p´ gina do autor na web podem ser encontrados pacotes de funcoes
ı a ¸˜
para estes programas al´ m de links para as p´ ginas do SciLab e do Maxima e v´ rias p´ ginas interativas que
e a a a
podem auxiliar na aprendizagem.
No fim de cada cap´tulo temos um “Teste do Cap´tulo”, onde o aluno pode avaliar os seus conhecimentos.
ı ı
Os Exerc´cios Num´ ricos e os Exerc´cios usando o M ATLAB est˜ o resolvidos apos o ultimo cap´tulo utili-
ı e ı a ´ ´ ı
zando o M ATLAB . Desta forma o leitor que n˜ o estiver interessado em usar o software pode obter apenas
a
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

9. Pref´ cio
a ix
as respostas dos exerc´cios, enquanto aquele que tiver algum interesse, pode ficar sabendo como os exerc´cios
ı ı
poderiam ser resolvidos fazendo uso do M ATLAB e do pacote gaal.
¸˜ ˜
Gostaria de agradecer aos professores que colaboraram apresentando correcoes, cr´ticas e sugestoes, entre
ı
eles Joana Darc A. S. da Cruz, Rinaldo Vieira da Silva Junior e S´ rgio Guilherme de Assis Vasconcelos.
e
Marco 2012
¸ Reginaldo J. Santos

10. x Pref´ cio
a
Hist´ rico
o
c ¸ ¸˜ ¸˜
Mar¸ o 2012 Mudanca na formatacao do texto. Algumas correcoes. V´ rias figuras foram refeitas. Foram acres-
a
centados o exerc´cio 5.2.12 sobre a propriedade refletora da elipse e o exerc´cio 5.2.13 sobre a propriedade
ı ı
refletora da hip´ rbole.
e
c ı ı ¸˜
Mar¸ o 2010 Foram acrescentados dois exerc´cios e dois itens em um exerc´cio na Secao 5.2 e dois itens em um
¸˜ ¸˜
exerc´cio na Secao 6.3. Foram escritas as respostas dos exerc´cios das Secoes 5.2. e 6.3.
ı ı
¸˜
Julho 2009 Algumas correcoes. V´ rias figuras foram refeitas.
a
¸˜ ` ¸˜
Mar¸ o 2008 Algumas correcoes. Foram acrescentados dois exerc´cios a Secao 4.3. As respostas de alguns
c ı
exerc´cios foram reescritas.
ı
Mar¸ o 2007 V´ rias figuras foram refeitas e outras acrescentadas. Foi acrescentado um item ao Teorema 2.13
c a
na p´ gina 104. Foram reescritos o Exemplo 3.12 e o Corol´ rio 3.10.
a a
c ı ¸˜ `
Mar¸ o 2006 Os Cap´tulos 1 e 2 foram reescritos. Foi acrescentada uma aplicacao as Cadeias de Markov. Foram
acrescentados v´ rios exerc´cios aos Cap´tulos 3 e 4. O Cap´tulo 5 foi reescrito. Foram escritas as respostas
a ı ı ı
¸˜ ` ¸˜
dos exerc´cios das Secoes 4.3. e 6.1. Foram acrescentados exerc´cios num´ ricos as Secoes 4.3 e 5.1 e
ı ı e
´ ` ¸˜
exerc´cios teoricos as Secoes 3.1, 4.2, 5.1 e 7.3.
ı
¸˜ `
Julho 2004 Foi acrescentada uma aplicacao a criptografia (Exemplo na p´ gina 88). Foi acrescentado um
a
¸˜ ¸˜ ´
exerc´cio na Secao 1.1. Foi inclu´da a demonstracao de que toda matriz e equivalente por linhas a uma
ı ı
´
unica matriz escalonada reduzida. Este resultado era o Teorema 1.4 na p´ gina 26 que passou para o
a
¸˜ ¸˜
Apˆ ndice II da Secao 1.2. O Teorema 1.4 agora cont´ m as propriedades da relacao “ser equivalente por
e e
¸˜ ı ı ¸˜
linhas” com a demonstracao. No Cap´tulo 3 foram acrescentados 2 exerc´cios na secao 3.1, 1 exerc´cio na
ı
¸˜ ¸˜
Secao 3.2. No Cap´tulo 4 a Secao 4.1 foi reescrita e foram acrescentados 2 exerc´cios.
ı ı
c ı ´
Mar¸ o 2002 Criado a partir do texto ’Geometria Anal´tica e Algebra Linear’ para ser usado numa disciplina
de Geometria Anal´tica.
ı
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

11. Pref´ cio
a xi
Sugest˜ o de Cronograma
a
Cap´tulo 1
ı ¸˜
Secoes 1.1 e 1.2 8 aulas
Cap´tulo 2
ı ¸˜
Secoes 2.1 e 2.2 8 aulas
Cap´tulo 3
ı ¸˜
Secoes 3.1 e 3.2 8 aulas
Cap´tulo 4
ı ¸˜
Secoes 4.1 e 4.2 8 aulas
Cap´tulo 5
ı ¸˜
Secoes 5.1 e 5.2 8 aulas
Cap´tulo 6
ı ¸˜
Secoes 6.1 a 6.3 12 aulas
Cap´tulo 7
ı ¸˜
Secoes 7.1 a 7.3 12 aulas
Total 64 aulas
Marco 2012
¸ Reginaldo J. Santos

12. xii Pref´ cio
a
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

13. 1
Matrizes e Sistemas Lineares
1.1 Matrizes
Uma matriz A, m × n (m por n), e uma tabela de mn numeros dispostos em m linhas
´ ´
e n colunas  
a11 a12 . . . a1n
 a21 a22 . . . a2n 
A= . . .
 
 . . ... . 
.
am1 am2 ... amn
A i-´ sima linha de A e
e ´
ai1 ai2 ... ain ,
1

14. 2 Matrizes e Sistemas Lineares
para i = 1, . . . , m e a j-´ sima coluna de A e
e ´
 
a1j
 a2j 
,
 
 .
.
 . 
amj
para j = 1, . . . , n. Usamos tamb´ m a notacao A = ( aij )m×n . Dizemos que aij ou [ A]ij
e ¸˜
e o elemento ou a entrada de posicao i, j da matriz A.
´ ¸˜
Se m = n, dizemos que A e uma matriz quadrada de ordem n e os elementos
´
a11 , a22 , . . . , ann formam a diagonal (principal) de A.
Exemplo 1.1. Considere as seguintes matrizes:
1 2 −2 1 1 3 0
A= , B= , C= ,
3 4 0 3 2 4 −2


1
D= 1 3 −2 , E= 4  eF= 3 .
−3
As matrizes A e B s˜ o 2 × 2. A matriz C e 2 × 3, D e 1 × 3, E e 3 × 1 e F e 1 × 1.
a ´ ´ ´ ´
¸˜
De acordo com a notacao que introduzimos, exemplos de elementos de algumas das
matrizes dadas acima s˜ o a12 = 2, c23 = −2, e21 = 4, [ A]22 = 4, [ D ]12 = 3.
a
´ ´
Uma matriz que so possui uma linha e chamada matriz linha, e uma matriz que
so possui uma coluna e chamada matriz coluna, No Exemplo 1.1 a matriz D e uma
´ ´ ´
matriz linha e a matriz E e uma matriz coluna.
´
Dizemos que duas matrizes s˜ o iguais se elas tˆ m o mesmo tamanho e os elementos
a e
correspondentes s˜ o iguais, ou seja, A = ( aij )m×n e B = (bij ) p×q s˜ o iguais se m = p,
a a
n = q e aij = bij para i = 1, . . . , m e j = 1, . . . , n.
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

15. 1.1 Matrizes 3
¸˜ ` ¸˜ ´
Vamos definir operacoes matriciais an´ logas as operacoes com numeros e provar
a
¸˜
propriedades que s˜ o v´ lidas para essas operacoes. Veremos, mais tarde, que um
a a
¸˜ ´ ¸˜
sistema de equacoes lineares pode ser escrito em termos de uma unica equacao ma-
tricial.
¸˜
Vamos, agora, introduzir as operacoes matriciais.
¸˜
1.1.1 Operacoes com Matrizes
¸˜
Definicao 1.1. A soma de duas matrizes de mesmo tamanho A = ( aij )m×n e B = (bij )m×n e definida como
´
sendo a matriz m × n
C = A+B
obtida somando-se os elementos correspondentes de A e B, ou seja,
cij = aij + bij ,
para i = 1, . . . , m e j = 1, . . . , n. Escrevemos tamb´ m [ A + B]ij = aij + bij .
e
Exemplo 1.2. Considere as matrizes:
1 2 −3 −2 1 5
A= , B=
3 4 0 0 3 −4
Se chamamos de C a soma das duas matrizes A e B, ent˜ o
a
1 + (−2) 2+1 −3 + 5 −1 3 2
C = A+B = =
3+0 4+3 0 + (−4) 3 7 −4
Marco 2012
¸ Reginaldo J. Santos

16. 4 Matrizes e Sistemas Lineares
¸˜
Definicao 1.2. A multiplica¸ ao de uma matriz A = ( aij )m×n por um escalar (numero) α e definida pela matriz
c˜ ´ ´
m×n
B = αA
obtida multiplicando-se cada elemento da matriz A pelo escalar α, ou seja,
bij = α aij ,
para i = 1, . . . , m e j = 1, . . . , n. Escrevemos tamb´ m [αA]ij = α aij . Dizemos que a matriz B e um multiplo
e ´ ´
escalar da matriz A.
 
−2 1
Exemplo 1.3. O produto da matriz A =  0 3  pelo escalar −3 e dado por
´
5 −4
   
(−3)(−2) (−3) 1 6 −3
−3 A =  (−3) 0 (−3) 3  =  0 −9  .
(−3) 5 (−3)(−4) −15 12
¸˜
Definicao 1.3. O produto de duas matrizes, tais que o numero de colunas da primeira matriz e igual ao
´ ´
numero de linhas da segunda, A = ( aij )m× p e B = (bij ) p×n e definido pela matriz m × n
´ ´
C = AB
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

17. 1.1 Matrizes 5
obtida da seguinte forma:
cij = ai1 b1j + ai2 b2j + . . . + aip b pj , (1.1)
para i = 1, . . . , m e j = 1, . . . , n. Escrevemos tamb´ m [ AB]ij = ai1 b1j + ai2 b2j + . . . + aip b pj .
e
A equacao (1.1) est´ dizendo que o elemento i, j do produto e igual a soma dos pro-
¸˜ a ´ `
dutos dos elementos da i-´ sima linha de A pelos elementos correspondentes da j-
e
esima coluna de B.
´
a11 a12 . . . a1p
 
 
   .
. .
. b11 b1j b1n
c11 ... c1n ... ...

 . ... . 
. .     b21
... b2j ... b2n 

. .

= ai1 ai2 . . . aip .
 
 . cij .  . ... .
. ... .
.

. . .
    
cm1 ... cmn  .
. .
.

... ...

 . ... .  b p1 b b pn
pj
am1 am2 ... amp
¸˜
A equacao (1.1) pode ser escrita de forma compacta usando a nota¸ ao de somatorio.
c˜ ´
p
[ AB]ij = ai1 b1j + ai2 b2j + . . . + aip b pj = ∑ aik bkj
k =1
p
e dizemos “somatorio de k variando de 1 a p de aik bkj ”. O s´mbolo
´ ı ∑ significa que
k =1
estamos fazendo uma soma em que o ´ndice k est´ variando de k = 1 at´ k = p.
ı a e
¸˜ ´
Algumas propriedades da notacao de somatorio est˜ o explicadas no Apˆ ndice I na
a e
p´ gina 27.
a
Marco 2012
¸ Reginaldo J. Santos

18. 6 Matrizes e Sistemas Lineares
Exemplo 1.4. Considere as matrizes:
 
−2 1 0
1 2 −3
A= , B= 0 3 0 .
3 4 0
5 −4 0
Se chamamos de C o produto das duas matrizes A e B, ent˜ o
a
1 (−2) + 2 · 0 + (−3) 5 1 · 1 + 2 · 3 + (−3) (−4) 0 −17 19 0
C = AB = = .
3 (−2) + 4 · 0 + 0 · 5 3 · 1 + 4 · 3 + 0 (−4) 0 −6 15 0
Observa¸ ao. No exemplo anterior o produto BA n˜ o est´ definido (por quˆ ?). Entretanto, mesmo quando ele
c˜ a a e
est´ definido, BA pode n˜ o ser igual a AB, ou seja, o produto de matrizes n˜ o e comutativo, como mostra o
a a a ´
exemplo seguinte.
1 2 −2 1
Exemplo 1.5. Sejam A = 3 4
eB=
0 3
. Ent˜ o,
a
−2 7 1 0
AB = e BA = .
−6 15 9 12
´
Vamos ver no proximo exemplo como as matrizes podem ser usadas para descrever
¸˜
quantitativamente um processo de producao.
Exemplo 1.6. Uma industria produz trˆ s produtos, X, Y e Z, utilizando dois tipos
´ e
de insumo, A e B. Para a manufatura de cada kg de X s˜ o utilizados 1 grama do
a
insumo A e 2 gramas do insumo B; para cada kg de Y, 1 grama de insumo A e 1
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

19. 1.1 Matrizes 7
grama de insumo B e, para cada kg de Z, 1 grama de A e 4 gramas de B. Usando
matrizes podemos determinar quantos gramas dos insumos A e B s˜ o necess´ rios
a a
na producao de x kg do produto X, y kg do produto Y e z kg do produto Z.
¸˜
X Y Z 

x kg de X produzidos
gramas de A/kg 1 1 1
= A X=  y  kg de Y produzidos
gramas de B/kg 2 1 4
z kg de Z produzidos
x+y+z gramas de A usados
AX =
2x + y + 4z gramas de B usados
¸˜
Definicao 1.4. A transposta de uma matriz A = ( aij )m×n e definida pela matriz n × m
´
B = At
obtida trocando-se as linhas com as colunas, ou seja,
bij = a ji ,
para i = 1, . . . , n e j = 1, . . . , m. Escrevemos tamb´ m [ At ]ij = a ji .
e
Exemplo 1.7. As transpostas das matrizes
1 2 −2 1 1 3 0
A= , B= e C= s˜ o
a
3 4 0 3 2 4 −2
 
1 2
1 3 −2 0
At = , Bt = e Ct =  3 4 .
2 4 1 3
0 −2
Marco 2012
¸ Reginaldo J. Santos

20. 8 Matrizes e Sistemas Lineares
a a ´
A seguir, mostraremos as propriedades que s˜ o v´ lidas para a algebra matricial.
a a ` a a ´
V´ rias propriedades s˜ o semelhantes aquelas que s˜ o v´ lidas para os numeros reais,
mas deve-se tomar cuidado com as diferencas. Uma propriedade importante que
¸
´ a ´ a ´ a ´
e v´ lida para os numeros reais, mas n˜ o e v´ lida para as matrizes e a comutativi-
dade do produto, como foi mostrado no Exemplo 1.5. Por ser compacta, usaremos
¸˜ ´ ¸˜
a notacao de somatorio na demonstracao de v´ rias propriedades. Algumas proprie-
a
¸˜
dades desta notacao est˜ o explicadas no Apˆ ndice I na p´ gina 27.
a e a
´
1.1.2 Propriedades da Algebra Matricial
Teorema 1.1. Sejam A, B e C matrizes com tamanhos apropriados, α e β escalares. S˜ o v´ lidas as seguintes propriedades
a a
para as opera¸ oes matriciais:
c˜
(a) (comutatividade) A + B = B + A;
(b) (associatividade) A + ( B + C ) = ( A + B) + C;
¯ ¯
(c) (elemento neutro) A matriz 0, m × n, definida por [0]ij = 0, para i = 1, . . . , m, j = 1, . . . , n e tal que
´
¯
A + 0 = A,
¯´
para toda matriz A, m × n. A matriz 0 e chamada matriz nula m × n.
(d) (elemento sim´trico) Para cada matriz A, existe uma unica matriz − A, definida por [− A]ij = − aij tal que
e ´
¯
A + (− A) = 0.
(e) (associatividade) α( βA) = (αβ) A;
(f) (distributividade) (α + β) A = αA + βA;
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

21. 1.1 Matrizes 9
(g) (distributividade) α( A + B) = αA + αB;
(h) (associatividade) A( BC ) = ( AB)C;
(i) (elemento neutro) Para cada inteiro positivo p a matriz, p × p,
 
1 0 ... 0
 0 1 ... 0 
Ip =  . . ,
 
 . .. .
. . . 
0 0 ... 1
chamada matriz identidade e tal que
´
A In = Im A = A, para toda matriz A = ( aij )m×n .
(j) (distributividade) A( B + C ) = AB + AC e ( B + C ) A = BA + CA;
(k) α( AB) = (αA) B = A(αB);
(l) ( At )t = A;
(m) ( A + B)t = At + Bt ;
(n) (αA)t = α At ;
(o) ( AB)t = Bt At ;
¸˜
Demonstracao. Para provar as igualdades acima, devemos mostrar que os elementos
da matriz do lado esquerdo s˜ o iguais aos elementos correspondentes da matriz do
a
a a ´
lado direito. Ser˜ o usadas v´ rias propriedades dos numeros sem cit´ -las explicita-
a
mente.
(a) [ A + B]ij = aij + bij = bij + aij = [ B + A]ij ;
Marco 2012
¸ Reginaldo J. Santos

22. 10 Matrizes e Sistemas Lineares
(b) [ A + ( B + C )]ij = aij + [ B + C ]ij = aij + (bij + cij ) = ( aij + bij ) + cij = [ A +
B]ij + cij = [( A + B) + C ]ij ;
(c) Seja X uma matriz m × n tal que
A+X = A (1.2)
para qualquer matriz A, m × n. Comparando os elementos correspondentes,
temos que
aij + xij = aij ,
ou seja, xij = 0, para i = 1 . . . , m e j = 1 . . . , n. Portanto, a unica matriz que
´
´
satisfaz (1.2) e a matriz em que todos os seus elementos s˜ o iguais a zero. De-
a
notamos a matriz X por 0. ¯
(d) Dada uma matriz A, m × n, seja X uma matriz m × n, tal que
¯
A + X = 0. (1.3)
Comparando os elementos correspondentes, temos que
aij + xij = 0 ,
ou seja, xij = − aij , para i = 1 . . . , m e j = 1 . . . , n. Portanto, a unica matriz que
´
´
satisfaz (1.3) e a matriz em que todos os seus elementos s˜ o iguais aos sim´ tricos
a e
dos elementos de A. Denotamos a matriz X por − A.
(e) [α( βA)]ij = α[ βA]ij = α( βaij ) = (αβ) aij = [(αβ) A]ij .
(f) [(α + β) A]ij = (α + β) aij = (αaij ) + ( βaij ) = [αA]ij + [ βA]ij = [αA + βA]ij .
(g) [α( A + B)]ij = α[ A + B]ij = α( aij + bij ) = αaij + αbij = [αA]ij + [αB]ij
= [αA + αB]ij .
(h) A demonstracao deste item e a mais trabalhosa. Sejam A, B e C matrizes m × p,
¸˜ ´
p × q e q × n respectivamente. A notacao de somatorio aqui pode ser muito util,
¸˜ ´ ´
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

23. 1.1 Matrizes 11
pelo fato de ser compacta.
p p q p q
[ A( BC )]ij = ∑ aik [ BC ]kj = ∑ aik ( ∑ bkl clj ) = ∑ ∑ aik (bkl clj ) =
k =1 k =1 l =1 k =1 l =1
p q q p q p
= ∑ ∑ (aik bkl )clj = ∑ ∑ (aik bkl )clj = ∑ ( ∑ aik bkl )clj =
k =1 l =1 l =1 k =1 l =1 k =1
q
= ∑ [ AB]il clj = [( AB)C]ij .
l =1
´
(i) Podemos escrever a matriz identidade em termos do delta de Kronecker que e
definido por
1, se i = j
δij =
0, se i = j
como [ In ]ij = δij . Assim,
n n
[ AIn ]ij = ∑ aik [ In ]kj = ∑ aik δkj = aij .
k =1 k =1
´ p a
A outra igualdade e an´ loga. p p
(j) [ A( B + C )]ij = ∑ aik [ B + C ]kj = ∑ aik (bkj + ckj ) = ∑ (aik bkj + aik ckj ) =
k =1 k =1 k =1
p p
= ∑ aik bkj + ∑ aik ckj = [ AB]ij + [ AC]ij = [ AB + AC]ij .
k =1 k =1
´
A outra igualdade e inteiramente an´ loga a anterior e deixamos como exerc´cio.
a ı
p p
(k) [α( AB)]ij = α ∑ aik bkj = ∑ (αaik )bkj = [(αA) B]ij e
k =1 k =1
p p
[α( AB)]ij = α ∑ aik bkj = ∑ aik (αbkj ) = [ A(αB)]ij .
k =1 k =1
Marco 2012
¸ Reginaldo J. Santos

24. 12 Matrizes e Sistemas Lineares
(l) [( At )t ]ij = [ At ] ji = aij .
(m) [( A + B)t ]ij = [ A + B] ji = a ji + b ji = [ At ]ij + [ Bt ]ij .
(n) [(αA)t ]ij = [αA] ji = αa ji = α[ At ]ij = [αAt ]ij .
p p p
(o) [( AB)t ]ij = [ AB] ji = ∑ a jk bki = ∑ [ At ]kj [ Bt ]ik = ∑ [ Bt ]ik [ At ]kj = [ Bt At ]ij .
k =1 k =1 k =1
A diferen¸ a entre duas matrizes de mesmo tamanho A e B e definida por
c ´
A − B = A + (− B),
ou seja, e a soma da matriz A com a sim´ trica da matriz B.
´ e
Sejam A uma matriz n × n e p um inteiro positivo. Definimos a potˆ ncia p de A, por
e
A p = A . . . A. E para p = 0, definimos A0 = In .
p vezes
Exemplo 1.8. Vamos verificar se para matrizes A e B, quadradas, vale a igualdade
( A + B)( A − B) = A2 − B2 . (1.4)
Usando a propriedade (i) do teorema anterior obtemos
( A + B)( A − B) = ( A + B) A + ( A + B)(− B)
= AA + BA − AB − BB = A2 + BA − AB − B2
Assim, ( A + B)( A − B) = A2 − B2 se, e somente se, BA − AB = 0, ou seja, se, e
somente se, AB = BA. Como o produto de matrizes n˜ o e comutativo, a conclus˜ o e
a ´ a ´
que a igualdade (1.4), n˜ o vale para matrizes em geral. Como contra-exemplo basta
a
tomarmos duas matrizes que n˜ o comutem entre si. Sejam
a
0 0 1 0
A= e B= .
1 1 1 0
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

25. 1.1 Matrizes 13
Para estas matrizes
1 0 −1 0 0 0 1 0
A+B = , A−B = , A2 = A = , B2 = B = .
2 1 0 1 1 1 1 0
Assim,
−1 0 −1 0
( A + B)( A − B) = = = A2 − B2 .
−2 1 0 1
¸˜
1.1.3 Aplicacao: Cadeias de Markov
¸˜ ´
Vamos supor que uma populacao e dividida em trˆ s estados (por exemplo: ricos,
e
classe m´ dia e pobres) e que em cada unidade de tempo a probabilidade de mudanca
e ¸
´
de um estado para outro seja constante no tempo, so dependa dos estados. Este
´
processo e chamado cadeia de Markov.
Seja tij a probabilidade de mudanca do estado j para o estado i em uma unidade de
¸
tempo (geracao). Tome cuidado com a ordem dos ´ndices. A matriz
¸˜ ı
 1 2 3 
t11 t12 t13 1
T =  t21 t22 t23  2
t31 t32 t33 3
´ ¸˜ ¸˜
e chamada matriz de transi¸ ao. A distribuicao da populacao inicial entre os trˆ s
c˜ e
estados pode ser descrita pela seguinte matriz:
 
p1 est´ no estado 1
a
P0 =  p2  est´ no estado 2
a
p3 est´ no estado 3
a
A matriz P0 caracteriza a distribuicao inicial da populacao entre os trˆ s estados e e
¸˜ ¸˜ e ´
´ ¸˜
chamada vetor de estado. Apos uma unidade de tempo a populacao estar´ dividida
a
Marco 2012
¸ Reginaldo J. Santos

26. 14 Matrizes e Sistemas Lineares
entre os trˆ s estados da seguinte forma
e
 
t11 p1 + t12 p2 + t13 p3 estar´ no estado 1
a
P1 =  t21 p1 + t22 p2 + t23 p3  estar´ no estado 2
a
t31 p1 + t32 p2 + t33 p3 estar´ no estado 3
a
Lembre-se que tij e a probabilidade de mudanca do estado j para o estado i. Assim
´ ¸
´ ´
o vetor de estado apos uma unidade de tempo e dada pelo produto de matrizes:
P1 = TP0 .
Exemplo 1.9. Vamos considerar a matriz de transicao
¸˜
1 2 3
 1 1 
2 4 0 1
1 1 1  2 (1.5)
T = 

2 2 2 
0 1 1 3
4 2
e o vetor de estados inicial
 1 
3 est´ no estado 1
a
P0 =  1  est´ no estado 2
a (1.6)
3
1 est´ no estado 3
a
3
¸˜ ¸˜
que representa uma populacao dividida de forma que 1/3 da populacao est´ em
a
cada estado.
´
Apos uma unidade de tempo a matriz de estado ser´ dada por
a
 1 1  1   1 
2 4 0 3 4
P1 = TP0 =  1 1 1 1 1
=
    
2 2 2  3 2 
1 1 1 1
0 4 2 3 4
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

27. 1.1 Matrizes 15
¸˜ ´
Como estamos assumindo que em cada unidade de tempo a matriz de transicao e a
mesma, ent˜ o apos k unidades de tempo a populacao estar´ dividida entre os trˆ s
a ´ ¸˜ a e
estados segundo a matriz de estado
Pk = TPk−1 = T 2 Pk−2 = · · · = T k P0
Assim a matriz T k d´ a transicao entre k unidades de tempo.
a ¸˜
Marco 2012
¸ Reginaldo J. Santos

28. 16 Matrizes e Sistemas Lineares
Exerc´cios Num´ ricos (respostas na p´ gina 510)
ı e a
1.1.1. Considere as seguintes matrizes
2 0 0 4 −6 9 −7
A= , B= , C=
6 7 2 −8 7 −3 −2
   
−6 4 0 6 9 −9
D =  1 1 4 , E =  −1 0 −4 
−6 0 6 −6 0 −1
Se for poss´vel calcule:
ı
(a) AB − BA,
(b) 2C − D,
(c) (2D t − 3Et )t ,
(d) D2 − DE.
1.1.2. Conhecendo-se somente os produtos AB e AC, como podemos calcular A( B + C ), Bt At , C t At e ( ABA)C?
1.1.3. Considere as seguintes matrizes
 
2 −1
−3 2 1
A= , B= 2 0 
1 2 −1
0 3
   
−2 1 −1 d1 0 0
C= 0 1 1  , D =  0 d2 0 
−1 0 1 0 0 d3
     
1 0 0
E1 =  0  , E2 =  1  , E3 =  0 
0 0 1
Verifique que:
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

29. 1.1 Matrizes 17
(a) AB e diferente de BA.
´
(b) AEj e a j-´ sima coluna de A, para j = 1, 2, 3 e Eit B e a i-´ sima linha de B, para i = 1, 2, 3 (o caso geral
´ e ´ e
est´ no Exerc´cio 1.1.15 na p´ gina 21).
a ı a
     
−2 1 −1
(c) CD = [ d1 C1 d2 C2 d3 C3 ], em que C1 =  0 , C2 =  1  e C3 =  1 , s˜ o as colunas de C
a
−1 0 1
(o caso geral est´ no Exerc´cio 1.1.16 (a) na p´ gina 22).
a ı a
 
d1 C1
(d) DC =  d2 C2 , em que C1 = −2 1 −1 , C2 = 0 1 1 e C3 = −1 0 1 s˜ o as a
d3 C3
linhas de C (o caso geral est´ no Exerc´cio 1.1.16 (b) na p´ gina 22).
a ı a
   
2 −1
(e) Escrevendo B em termos das suas colunas, B = [ B1 B2 ], em que B1 =  2  e B2 =  0 , o
0 3
produto AB pode ser escrito como AB = A [ B1 B2 ] = [ AB1 AB2 ] (o caso geral est´ no Exerc´cio
a ı
1.1.17 (a) na p´ gina 23).
a
(f) escrevendo A em termos das suas linhas, A1 = −3 2 1 e A2 = 1 2 −1 , o produto
A1 A1 B
AB pode ser escrito como AB = B= (o caso geral est´ no Exerc´cio 1.1.17 (b) na
a ı
A2 A2 B
p´ gina 23).
a
1.1.4. Sejam  
x
1 −3 0
A= e X =  y .
0 4 −2
z
Verifique que xA1 + yA2 + zA3 = AX, em que A j e a j-´ sima coluna de A, para j = 1, 2, 3 (o caso geral
´ e
est´ no Exerc´cio 1.1.18 na p´ gina 24).
a ı a
1.1.5. Encontre um valor de x tal que ABt = 0, em que
A= x 4 −2 e B= 2 −3 5 .
Marco 2012
¸ Reginaldo J. Santos

30. 18 Matrizes e Sistemas Lineares
1
1 y
1.1.6. Mostre que as matrizes A = , em que y e uma numero real n˜ o nulo, verificam a equacao
´ ´ a ¸˜
y 1
X 2 = 2X.
0 1
1.1.7. Mostre que se A e B s˜ o matrizes que comutam com a matriz M =
a , ent˜ o AB = BA.
a
−1 0
1.1.8. (a) Determine todas as matrizes A, 2 × 2, diagonais (os elementos que est˜ o fora da diagonal s˜ o iguais
a a
a zero) que comutam com toda matriz B, 2 × 2, ou seja, tais que AB = BA, para toda matriz B, 2 × 2.
(b) Determine todas as matrizes A, 2 × 2, que comutam com toda matriz B, 2 × 2, ou seja, tais que
AB = BA, para toda matriz B, 2 × 2.
Exerc´cios usando o M ATLAB
ı
Uma vez inicializado o M ATLAB , aparecer´ na janela de comandos um prompt >> ou EDU>>. O prompt
a
significa que o M ATLAB est´ esperando um comando. Todo comando deve ser finalizado teclando-se
a
Enter. Comandos que foram dados anteriormente podem ser obtidos novamente usando as teclas ↑ e ↓.
Enquanto se estiver escrevendo um comando, este pode ser corrigido usando as teclas ←, →, Delete e
´ ´
Backspace. O M ATLAB faz diferenca entre letras maiusculas e minusculas.
¸
¸˜
No M ATLAB , pode-se obter ajuda sobre qualquer comando ou funcao. O comando
>> help
(sem o prompt >>) mostra uma listagem de todos os pacotes dispon´veis. Ajuda sobre um pacote es-
ı
ı ¸˜
pec´fico ou sobre um comando ou funcao espec´fica pode ser obtida com o comando
ı
>> help nome,
(sem a v´rgula e sem o prompt >>) em que nome pode ser o nome de um pacote ou o nome de um comando
ı
¸˜
ou funcao.
¸˜ ¸˜
Al´ m dos comandos e funcoes pr´ -definidas, escrevemos um pacote chamado gaal com funcoes es-
e e
ı ı ´
pec´ficas para a aprendizagem de Geometria Anal´tica e Algebra Linear. Este pacote pode ser obtido
gratuitamente atrav´ s da internet no endereco http://www.mat.ufmg.br/~regi, assim como um texto
e ¸
¸˜ ¸˜
com uma introducao ao M ATLAB e instrucoes de como instalar o pacote gaal. Depois deste pacote
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

31. 1.1 Matrizes 19
ser devidamente instalado, o comando help gaal no prompt do M ATLAB ¸˜
d´ informacoes sobre este
a
pacote.
¸˜
Mais informacoes sobre as capacidades do M ATLAB podem ser obtidas em [4, 17].
¸˜
Vamos descrever aqui alguns comandos que podem ser usados para a manipulacao de matrizes. Outros
comandos ser˜ o introduzidos a medida que forem necess´ rios.
a a
>> syms x y z diz ao M ATLAB ´
que as vari´ veis x y e z s˜ o simbolicas.
a a
>> A=[a11,a12,...,a1n;a21,a22,...; ...,amn] cria uma matriz, m por n, usando os elementos a11,
a12, ..., amn e a armazena numa vari´ vel de nome A. Por exemplo, >> A=[1,2,3;4,5,6] cria a matriz
a
1 2 3
A= ;
4 5 6
>> I=eye(n) cria a matriz identidade n por n e a armazena numa vari´ vel I;
a
>> O=zeros(n) ou >> O=zeros(m,n) cria a matriz nula n por n ou m por n, respectivamente, e a arma-
zena numa vari´ vel O;
a
´
>> A+B e a soma de A e B, ´
>> A-B e a diferenca A menos B,
¸
´
>> A*B e o produto de A por B, ´
>> num*A e o produto do escalar num por A,
´
>> A.’ e a transposta de A, >> A^k e a potˆ ncia A elevado a k.
´ e
>> A(:,j) e a coluna j da matriz A, >> A(i,:) e a linha i da matriz A.
´ ´
>> diag([d1,...,dn]) cria uma matriz diagonal, cujos elementos da diagonal s˜ o iguais aos elementos
a
da matriz [d1,...,dn], ou seja, s˜ o d1,...,dn.
a
>> A=sym(A) converte a matriz A numa matriz em que os elementos s˜ o armazenados no formato
a
´ ¸˜
simbolico. A funcao numeric faz o processo inverso.
>> solve(expr) determina a ¸˜
solucao da ¸˜
equacao expr=0. Por exemplo,
>> solve(x^2-4) determina as solucoes da equacao x2 − 4 = 0;
¸˜ ¸˜
Comando do pacote GAAL:
>> A=randi(n) ou >> A=randi(m,n) cria uma matriz n por n ou m por n, respectivamente, com elementos
inteiros aleatorios entre −5 e 5.
´
Marco 2012
¸ Reginaldo J. Santos

32. 20 Matrizes e Sistemas Lineares
1.1.9. Use o M ATLAB para calcular alguns membros da sequˆ ncia A, A2 , . . . , Ak , . . ., para
¨e
1 1 1
1 2 2 3
(a) A = 1 ; (b) A = 1 .
0 3 0 −5
¨e
A sequˆ ncia parece estar convergindo para alguma matriz? Se estiver, para qual?
1.1.10. Calcule as potˆ ncias das matrizes dadas a seguir e encontre experimentalmente (por tentativa!) o menor
e
inteiro k > 1 tal que (use o comando >> A=sym(A) depois de armazenar a matriz na vari´ vel A):
a
(a) Ak = I3 , em que  
0 0 1
A =  1 0 0 ;
0 1 0
(b) Ak = I4 , em que  
0 1 0 0
 −1 0 0 0 
A = 
 ;
0 0 0 1 
0 0 1 0
¯
(c) Ak = 0, em que  
0 1 0 0
 0 0 1 0 
A = 
 0
.
0 0 1 
0 0 0 0
e a ´
1.1.11. Vamos fazer um experimento no M ATLAB para tentar ter uma id´ ia do qu˜ o comum e encontrar ma-
trizes cujo produto comuta. No prompt do M ATLAB digite a seguinte linha:
>> c=0; for n=1:1000,A=randi(3);B=randi(3);if(A*B==B*A),c=c+1;end,end,c
(n˜ o esqueca das v´rgulas e pontos e v´rgulas!). O que esta linha est´ mandando o M ATLAB
a ¸ ı ı a ´
fazer e o
seguinte:
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

33. 1.1 Matrizes 21
• Criar um contador c e atribuir a ele o valor zero.
• Atribuir as vari´ veis A e B, 1000 matrizes 3 × 3 com entradas inteiras e aleatorias entre −5 e 5.
` a ´
• ´
Se AB=BA, ou seja, A e B comutarem, ent˜ o o contador c e acrescido de 1.
a
• ´
No final o valor existente na vari´ vel c e escrito.
a
Qual a conclus˜ o que vocˆ tira do valor obtido na vari´ vel c?
a e a
´
1.1.12. Faca um experimento semelhante ao anterior, mas para o caso em que cada uma das matrizes e diagonal,
¸
isto e, os elementos que est˜ o fora da diagonal s˜ o iguais a zero. Use a seta para cima ↑ para obter
´ a a
novamente a linha digitada e edite a linha no prompt do M ATLAB de forma a obter algo semelhante a `
linha:
>> c=0; for n=1:1000,A=diag(randi(1,3));B=diag(randi(1,3));if( ....
Qual a conclus˜ o que vocˆ tira do valor obtido na vari´ vel c?
a e a
´
1.1.13. Faca um experimento semelhante ao anterior, mas para o caso em que uma das matrizes e diagonal. Use
¸
a seta para cima ↑ para obter novamente a linha digitada e edite a linha no prompt do M ATLAB de
forma a obter a seguinte linha:
>> c=0; for n=1:1000,A=diag(randi(1,3));B=randi(3);if(A*B==B*A),c=c+1;A,B,end,end,c
Aqui s˜ o impressas as matrizes A e B quando elas comutarem. Qual a conclus˜ o que vocˆ tira deste
a a e
experimento? Qual a probabilidade de um tal par de matrizes comutarem?
1.1.14. Use o M ATLAB para resolver os Exerc´cios Num´ ricos.
ı e
Exerc´cios Teoricos
ı ´
     
1 0 0

 0 


 1 


 0 

0 0 .
.
1.1.15. Sejam E1 =   , E2 =  ,. . . , En =   matrizes n × 1.
     
. . .

 .
.



 .
.



 0


0 0 1
Marco 2012
¸ Reginaldo J. Santos

34. 22 Matrizes e Sistemas Lineares
(a) Mostre que se
 
a11 a12 ... a1n
 a21 a22 ... a2n 
A=
 
.
. .
. 
 . ... . 
am1 am2 ... amn
e uma matriz m × n, ent˜ o AEj e igual a coluna j da matriz A.
´ a ´ `
(b) Mostre que se
 
b11 b12 ... b1m
 b21 b22 ... b2m 
B= ,
 
.
. .
.
 . ... . 
bn1 bn2 ... bnm
e uma matriz n × m ent˜ o Eit B e igual a linha i da matriz B.
´ a ´ `
1.1.16. Seja
 
λ1 0 ... 0
 0 λ2 ... 0 
D=
 
.
. .. .
. 
 . . . 
0 ... 0 λn
uma matriz diagonal n × n, isto e, os elementos que est˜ o fora da diagonal s˜ o iguais a zero. Seja
´ a a
 
a11 a12 ... a1n
 a21 a22 ... a2n 
A= .
 
.
. .
.
 . ... . 
an1 an2 ... ann
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

35. 1.1 Matrizes 23
(a) Mostre que o produto AD e obtido da matriz A multiplicando-se cada coluna j por λ j , ou seja, se
´
 
a1j
A = [ A1 A2 . . . An ], em que A j =  .  e a coluna j de A, ent˜ o
 . 
. ´ a
anj
AD = [ λ1 A1 λ2 A2 . . . λn An ].
(b) Mostre que  produto DA e obtido da matriz A multiplicando-se cada linha i por λi , ou seja, se
 o ´
A1
 A2 
A =  . , em que Ai = [ ai1 . . . ain ] e a linha i de A, ent˜ o
´ a
 
 . 
.
An
 
λ1 A1
 λ2 A2 
DA =  .
 
.
.
 . 
λn An
1.1.17. Sejam A e B matrizes m × p e p × n, respectivamente.

b1j
(a) Mostre que a j-´ sima coluna do produto AB e igual ao produto ABj , em que Bj =  .  e a
 . 
e ´ . ´
b pj
j-´ sima coluna de B, ou seja, se B = [ B1 . . . Bn ], ent˜ o
e a
AB = A[ B1 . . . Bn ] = [ AB1 . . . ABn ];
(b) Mostre que a i-´ sima linha do produto AB e igual ao produto Ai B, em que Ai = [ ai1 . . . aip ] e a
e ´ ´
Marco 2012
¸ Reginaldo J. Santos

36. 24 Matrizes e Sistemas Lineares
 
A1
 A2 
i-´ sima linha de A, ou seja, se A = 
e , ent˜ o
a
 
.
.
 . 
Am
   
A1 A1 B
 A2   A2 B 
AB =  B =  .
   
.
. .
.
 .   . 
Am Am B
 
x1
 . 
1.1.18. Seja A uma matriz m × n e X =  . 
. uma matriz n × 1. Prove que
xn
n
AX = ∑ xj Aj, em que A j e a j-´ sima coluna de A. (Sugest˜ o: Desenvolva o lado direito e che-
´ e a
j =1
gue ao lado esquerdo.)
1.1.19. ´ ¯ a ¯
(a) Mostre que se A e uma matriz m × n tal que AX = 0, para toda matriz X, n × 1, ent˜ o A = 0.
(Sugest˜ o: use o Exerc´cio 15 na p´ gina 21.)
a ı a
(b) Sejam B e C matrizes m × n, tais BX = CX, para todo X, n × 1. Mostre que B = C. (Sugest˜ o: use o
a
item anterior.)
1.1.20. Mostre que a matriz identidade In e a unica matriz tal que A In = In A = A para qualquer matriz A,
´ ´
n × n. (Sugest˜ o: Seja Jn uma matriz tal que A Jn = Jn A = A. Mostre que Jn = In .)
a
1.1.21. Se AB = BA e p e um inteiro positivo, mostre que ( AB) p = A p B p .
´
1.1.22. Sejam A, B e C matrizes n × n.
(a) ( A + B)2 = A2 + 2AB + B2 ? E se AB = BA? Justifique.
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

37. 1.1 Matrizes 25
(b) ( AB)C = C ( AB)? E se AC = CA e BC = CB? Justifique.
(Sugest˜ o: Veja o Exemplo 1.8 na p´ gina 12.)
a a
1.1.23. ¯ ¯ ¯
(a) Se A e B s˜ o duas matrizes tais que AB = 0, ent˜ o A = 0 ou B = 0? Justifique.
a a
¯ ¯
(b) Se AB = 0, ent˜ o BA = 0? Justifique.
a
¯ ¯
(c) Se A e uma matriz tal que A2 = 0, ent˜ o A = 0? Justifique.
´ a
1.1.24. Dizemos que uma matriz A, n × n, e sim´ trica se At = A e e anti-sim´ trica se At = − A.
´ e ´ e
(a) Mostre que se A e sim´ trica, ent˜ o aij = a ji , para i, j = 1, . . . n e que se A e anti-sim´ trica, ent˜ o
´ e a ´ e a
aij = − a ji , para i, j = 1, . . . n. Portanto, os elementos da diagonal principal de uma matriz anti-
sim´ trica s˜ o iguais a zero.
e a
(b) Mostre que se A e B s˜ o sim´ tricas, ent˜ o A + B e αA s˜ o sim´ tricas, para todo escalar α.
a e a a e
(c) Mostre que se A e B s˜ o sim´ tricas, ent˜ o AB e sim´ trica se, e somente se, AB = BA.
a e a ´ e
(d) Mostre que se A e B s˜ o anti-sim´ tricas, ent˜ o A + B e αA s˜ o anti-sim´ tricas, para todo escalar α.
a e a a e
(e) Mostre que para toda matriz A, n × n, A + At e sim´ trica e A − At e anti-sim´ trica.
´ e ´ e
(f) Mostre que toda matriz quadrada A pode ser escrita como a soma de uma matriz sim´ trica e uma
e
anti-sim´ trica. (Sugest˜ o: Observe o resultado da soma de A + At com A − At .)
e a
1.1.25. Para matrizes quadradas A = ( aij )n×n definimos o tra¸ o de A como sendo a soma dos elementos da
c
n
diagonal (principal) de A, ou seja, tr( A) = ∑ aii .
i =1
(a) Mostre que tr( A + B) = tr( A) + tr( B).
(b) Mostre que tr(αA) = αtr( A).
(c) Mostre que tr( At ) = tr( A).
(d) Mostre que tr( AB) = tr( BA). (Sugest˜ o: Prove inicialmente para matrizes 2 × 2.)
a
Marco 2012
¸ Reginaldo J. Santos

38. 26 Matrizes e Sistemas Lineares
¯ a ¯
1.1.26. Seja A uma matriz n × n. Mostre que se AAt = 0, ent˜ o A = 0. (Sugest˜ o: use o traco.) E se a matriz A
a ¸
for m × n, com m = n?
a a ´
1.1.27. J´ vimos que o produto de matrizes n˜ o e comutativo. Entretanto, certos conjuntos de matrizes s˜ o
a
comutativos. Mostre que:
(a) Se D1 e D2 s˜ o matrizes diagonais n × n, ent˜ o D1 D2 = D2 D1 .
a a
(b) Se A e uma matriz n × n e
´
B = a0 In + a1 A + a2 A2 + . . . + ak Ak ,
em que a0 , . . . , ak s˜ o escalares, ent˜ o AB = BA.
a a
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

39. 1.1 Matrizes 27
e ¸˜
Apˆ ndice I: Notacao de Somat´ rio
o
¸˜ ´
S˜ o v´ lidas algumas propriedades para a notacao de somatorio:
a a
(a) O ´ndice do somatorio e uma vari´ vel muda que pode ser substitu´da por qual-
ı ´ ´ a ı
quer letra:
n n
∑ fi = ∑ f j .
i =1 j =1
´ ´
(b) O somatorio de uma soma pode ser escrito como uma soma de dois somatorios:
n n n
∑ ( f i + gi ) = ∑ f i + ∑ gi .
i =1 i =1 i =1
Pois,
n
∑ ( f i + g i ) = ( f 1 + g1 ) + . . . + ( f n + g n ) = ( f 1 + . . . + f n ) + ( g1 + . . . + g n ) =
i =1
n n
∑ f i + ∑ gi . Aqui foram aplicadas as propriedades associativa e comutativa
i =1 i =1
´
da soma de numeros.
´
(c) Se no termo geral do somatorio aparece um produto, em que um fator n˜ o de-
a
pende do ´ndice do somatorio, ent˜ o este fator pode “sair” do somatorio:
ı ´ a ´
n n
∑ f i gk = gk ∑ f i .
i =1 i =1
Pois,
n n
∑ f i gk = f 1 gk + . . . + f n gk = gk ( f 1 + . . . + f n ) = gk ∑ fi . Aqui foram apli-
i =1 i =1
¸˜
cadas as propriedades distributiva e comutativa do produto em relacao a soma
´
de numeros.
Marco 2012
¸ Reginaldo J. Santos

40. 28 Matrizes e Sistemas Lineares
´ ´
(d) Num somatorio duplo, a ordem dos somatorios pode ser trocada:
n m m n
∑ ∑ fij = ∑ ∑ fij .
i =1 j =1 j =1 i =1
Pois,
n m n
∑∑ f ij = ∑ ( fi1 + . . . + fim ) = ( f11 + . . . + f1m ) + . . . + ( f n1 + . . . + f nm ) =
i =1 j =1 i =1
m m n
( f 11 + . . . + f n1 ) + . . . + ( f 1m + . . . + f nm ) = ∑ ( f1j + . . . + f nj ) = ∑ ∑ fij . Aqui
j =1 j =1 i =1
´
foram aplicadas as propriedades comutativa e associativa da soma de numeros.
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

41. 1.2 ¸˜
Sistemas de Equacoes Lineares 29
1.2 ¸˜
Sistemas de Equacoes Lineares
´ ¸˜
Muitos problemas em v´ rias areas da Ciˆ ncia recaem na solucao de sistemas lineares.
a e
´
Vamos ver como a algebra matricial pode simplificar o estudo dos sistemas lineares.
Uma equa¸ ao linear em n vari´ veis x1 , x2 , . . . , xn e uma equacao da forma
c˜ a ´ ¸˜
a1 x1 + a2 x2 + . . . + a n x n = b ,
em que a1 , a2 , . . . , an e b s˜ o constantes reais;
a
´
Um sistema de equa¸ oes lineares ou simplesmente sistema linear e um conjunto de
c˜
¸˜ ´ ¸˜
equacoes lineares, ou seja, e um conjunto de equacoes da forma

 a11 x1 + a12 x2 +
 ... + a1n xn = b1
 a21 x1 + a22 x2 +

... + a2n xn = b2
.
. .
. .


 . . = . .
am1 x1 + am2 x2 + ... + amn xn = bm

em que aij e bk s˜ o constantes reais, para i, k = 1, . . . , m e j = 1, . . . , n.
a
¸˜
Usando o produto de matrizes que definimos na secao anterior, o sistema linear
¸˜
acima pode ser escrito como uma equacao matricial
A X = B,
em que
     
a11 a12 ... a1n x1 b1
 a21 a22 ... a2n   x2   b2 
A= , X= e B= .
     
.
. .
. .
.  .
.
 . ... .   .   . 
am1 am2 ... amn xn bm
Marco 2012
¸ Reginaldo J. Santos

42. 30 Matrizes e Sistemas Lineares
 
s1
 s2 
Uma solu¸ ao de um sistema linear e uma matriz S = 
c˜ ´ ¸˜
 tal que as equacoes
 
.
.
 . 
sn
do sistema s˜ o satisfeitas quando substitu´mos x1 = s1 , x2 = s2 , . . . , xn = sn . O
a ı
¸˜ ´
conjunto de todas as solucoes do sistema e chamado conjunto solu¸ ao ou solu¸ ao
c˜ c˜
geral do sistema. A matriz A e chamada matriz do sistema linear.
´
Exemplo 1.10. O sistema linear de duas equacoes e duas incognitas
¸˜ ´
x + 2y = 1
2x + y = 0
pode ser escrito como
1 2 x 1
= .
2 1 y 0
A solucao (geral) do sistema acima e x = −1/3 e y = 2/3 (verifique!) ou
¸˜ ´
1
−3
X= 2 .
3
´
Uma forma de resolver um sistema linear e substituir o sistema inicial por outro que
¸˜
tenha o mesmo conjunto solucao do primeiro, mas que seja mais f´ cil de resolver. O
a
´ ¸˜
outro sistema e obtido depois de aplicar sucessivamente uma s´ rie de operacoes, que
e
¸˜ ¸˜ ¸˜
n˜ o alteram a solucao do sistema, sobre as equacoes. As operacoes que s˜ o usadas
a a
s˜ o:
a
• Trocar a posicao de duas equacoes do sistema;
¸˜ ¸˜
• Multiplicar uma equacao por um escalar diferente de zero;
¸˜
• Somar a uma equacao outra equacao multiplicada por um escalar.
¸˜ ¸˜
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

43. 1.2 ¸˜
Sistemas de Equacoes Lineares 31
¸˜
Estas operacoes s˜ o chamadas de opera¸ oes elementares. Quando aplicamos
a c˜
¸˜ ¸˜
operacoes elementares sobre as equacoes de um sistema linear somente os coefici-
¸˜
entes do sistema s˜ o alterados, assim podemos aplicar as operacoes sobre a matriz
a
de coeficientes do sistema, que chamamos de matriz aumentada, ou seja, a matriz
 
a11 a12 ... a1n b1
 a21 a22 ... a2n b2 
[ A | B] =  . . .
 
.
 . . ... .
. . 
.
am1 am2 ... amn bm
Marco 2012
¸ Reginaldo J. Santos

44. 32 Matrizes e Sistemas Lineares
¸˜
Definicao 1.5. Uma opera¸ ao elementar sobre as linhas de uma matriz e uma das seguintes operacoes:
c˜ ´ ¸˜
¸˜
(a) Trocar a posicao de duas linhas da matriz;
(b) Multiplicar uma linha da matriz por um escalar diferente de zero;
´
(c) Somar a uma linha da matriz um multiplo escalar de outra linha.
´ ¸˜ ` ¸˜
O proximo teorema garante que ao aplicarmos operacoes elementares as equacoes
¸˜ a ´
de um sistema o conjunto solucao n˜ o e alterado.
Teorema 1.2. Se dois sistemas lineares AX = B e CX = D, s˜ o tais que a matriz aumentada [C | D] e obtida de [ A | B]
a ´
aplicando-se uma opera¸ ao elementar, ent˜ o os dois sistemas possuem as mesmas solu¸ oes.
c˜ a c˜
¸˜ ¸˜ ¸˜
Demonstracao. A demonstracao deste teorema segue-se de duas observacoes:
(a) Se X e solucao de um sistema, ent˜ o X tamb´ m e solucao do sistema obtido
´ ¸˜ a e ´ ¸˜
¸˜ ¸˜
aplicando-se uma operacao elementar sobre suas equacoes (verifique!).
(b) Se o sistema CX = D, e obtido de AX = B aplicando-se uma operacao elemen-
´ ¸˜
` ¸˜ `
tar as suas equacoes (ou equivalentemente as linhas da sua matriz aumentada),
ent˜ o o sistema AX = B tamb´ m pode ser obtido de CX = D aplicando-se
a e
¸˜ ` ¸˜ ¸˜
uma operacao elementar as suas equacoes, pois cada operacao elementar pos-
¸˜
sui uma operacao elementar inversa do mesmo tipo, que desfaz o que a anterior
fez (verifique!).
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

45. 1.2 ¸˜
Sistemas de Equacoes Lineares 33
Pela observacao (b), AX = B e CX = D podem ser obtidos um do outro aplicando-
¸˜
¸˜ ¸˜ ¸˜
se uma operacao elementar sobre as suas equacoes. E pela observacao (a), os dois
¸˜
possuem as mesmas solucoes.
¸˜ a
Dois sistemas que possuem o mesmo conjunto solucao s˜ o chamados sistemas equi-
¸˜
valentes. Portanto, segue-se do Teorema 1.2 que aplicando-se operacoes elementares
` ¸˜
as equacoes de um sistema linear obtemos sistemas equivalentes.
1.2.1 M´ todo de Gauss-Jordan
e
¸˜
O m´ todo que vamos usar para resolver sistemas lineares consiste na aplicacao de
e
¸˜ `
operacoes elementares as linhas da matriz aumentada do sistema at´ que obtenha-
e
mos uma matriz numa forma em que o sistema associado a esta matriz seja de f´ cil
a
¸˜
resolucao.
Vamos procurar obter uma matriz numa forma em que todas as linhas n˜ o nulas
a
a ˆ ´
possuam como primeiro elemento n˜ o nulo (chamado pivo) o numero 1 . Al´ m e
e ˆ
disso, se uma coluna cont´ m um pivo, ent˜ o todos os seus outros elementos ter˜ o
a a
que ser iguais a zero. Vamos ver no exemplo seguinte como conseguimos isso. Neste
exemplo veremos como a partir do faturamento e do gasto com insumos podemos
´
determinar quanto foi produzido de cada produto manufaturado em uma industria.
Exemplo 1.11. Uma industria produz trˆ s produtos, X, Y e Z, utilizando dois tipos
´ e
de insumo, A e B. Para a manufatura de cada kg de X s˜ o utilizados 1 grama do
a
insumo A e 2 gramas do insumo B; para cada kg de Y, 1 grama de insumo A e 1
grama de insumo B e, para cada kg de Z, 1 grama de A e 4 gramas de B. O preco ¸
´
de venda do kg de cada um dos produtos X, Y e Z e R$ 2,00, R$ 3,00 e R$ 5,00,
¸˜
respectivamente. Com a venda de toda a producao de X, Y e Z manufaturada com 1
´
kg de A e 2 kg de B, essa industria arrecadou R$ 2500,00. Vamos determinar quantos
kg de cada um dos produtos X, Y e Z foram vendidos.
Marco 2012
¸ Reginaldo J. Santos

46. 34 Matrizes e Sistemas Lineares
¸˜
Como vimos no Exemplo 1.6 na p´ gina 6, usando matrizes o esquema de producao
a
pode ser descrito da seguinte forma:
X Y Z 
gramas de A/kg 1 1 1 x kg de X produzidos
gramas de B/kg  2 1 4  = A X =  y  kg de Y produzidos
preco/kg
¸ 2 3 5 z kg de Z produzidos
   
x+y+z 1000 gramas de A usados
AX =  2x + y + 4z  =  2000  gramas de B usados
2x + 3y + 5z 2500 ¸˜
arrecadacao
Assim precisamos resolver o sistema linear

 x + y + z = 1000
2x + y + 4z = 2000
2x + 3y + 5z = 2500

´
cuja matriz aumentada e  
1 1 1 1000
 2 1 4 2000 
2 3 5 2500
1a elimina¸ ao:
. c˜
Vamos procurar para pivo da 1a linha um elemento n˜ o nulo da primeira coluna n˜ o
ˆ . a a
nula (se for o caso, podemos usar a troca de linhas para “trazˆ -lo” para a primeira
e
´
linha). Como o primeiro elemento da primeira coluna e igual a 1 ele ser´ o primeiro
a
pivo. Agora, precisamos “zerar” os outros elementos da 1a coluna, que e a coluna
ˆ . ´
do pivo, para isto, adicionamos a 2a linha, −2 vezes a 1a linha e adicionamos a 3a
ˆ ` . . ` .
linha, tamb´ m, −2 vezes a 1a linha.
e .
 
1 1 1 1000
−2×1a linha + 2a linha −→ 2a linha
. . .
0 −1 2 0
 
−2×1 a linha + 3a linha −→ 3a linha
. . .  
0 1 3 500
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

47. 1.2 ¸˜
Sistemas de Equacoes Lineares 35
2a elimina¸ ao:
. c˜
Olhamos para a sub-matriz obtida eliminando-se a 1a linha. Escolhemos para pivo
. ˆ
um elemento diferente de zero na 1a coluna n˜ o nula desta sub-matriz. Vamos esco-
. a
¸˜ ˆ
lher o elemento de posicao 2,2. Como temos que “fazer” o pivo igual a um, vamos
multiplicar a 2a linha por −1.
.
 
1 1 1 1000
−1×2a linha −→ 2a linha
. .  0 1 −2 0 
0 1 3 500
Agora, precisamos “zerar” os outros elementos da 2a coluna, que e a coluna do pivo,
. ´ ˆ
`
para isto, somamos a 1 a linha, −1 vezes a 2a e somamos a 3a linha, tamb´ m, −1 vezes
. . ` . e
a 2a .
.
 
1 0 3 1000
−1×2a linha + 1a linha −→ 1a linha
. . .
 0 1 −2 0 
−1×2a linha + 3a linha −→ 3a linha
. . .
0 0 5 500
3a elimina¸ ao:
. c˜
Olhamos para a sub-matriz obtida eliminando-se a 1a e a 2a linha. Escolhemos para
. .
pivo um elemento diferente de zero na 1a coluna n˜ o nula desta sub-matriz. Temos
ˆ . a
¸˜ ˆ
de escolher o elemento de posicao 3,3 e como temos de “fazer” o pivo igual a 1,
vamos multiplicar a 3a linha por 1/5.
.
 
1 0 3 1000
1 a a
5 ×3 linha −→ 3 linha
. .  0 1 −2 0 
0 0 1 100
Agora, precisamos “zerar” os outros elementos da 3a coluna, que e a coluna do pivo,
. ´ ˆ
`
para isto, somamos a 1 a linha, −3 vezes a 3a e somamos a 2a linha, 2 vezes a 2a .
. . ` . .
 
a linha + 1a linha −→ 1a linha 1 0 0 700
−3×3 . . .
 0 1 0 200 
2×3a linha + 2a linha −→ 2a linha
. . .
0 0 1 100
Marco 2012
¸ Reginaldo J. Santos

48. 36 Matrizes e Sistemas Lineares
´
Portanto o sistema dado e equivalente ao sistema

 x = 700
y = 200
z = 100

¸˜
que possui solucao geral dada por
   
x 700
X =  y  =  200  .
z 100
Portanto, foram vendidos 700 kg do produto X, 200 kg do produto Y e 100 kg do
produto Z.
´
A ultima matriz que obtivemos no exemplo anterior est´ na forma que chamamos
a
de escalonada reduzida.
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

49. 1.2 ¸˜
Sistemas de Equacoes Lineares 37
¸˜
Definicao 1.6. Uma matriz A = ( aij )m×n est´ na forma escalonada reduzida quando satisfaz as seguintes
a
¸˜
condicoes:
(a) Todas as linhas nulas (formadas inteiramente por zeros) ocorrem abaixo das linhas n˜ o nulas;
a
(b) O pivo (1o elemento n˜ o nulo de uma linha) de cada linha n˜ o nula e igual a 1;
ˆ . a a ´
ˆ ` ˆ
(c) O pivo de cada linha n˜ o nula ocorre a direita do pivo da linha anterior.
a
e ˆ
(d) Se uma coluna cont´ m um pivo, ent˜ o todos os seus outros elementos s˜ o iguais a zero.
a a
Se uma matriz satisfaz as propriedades (a) e (c), mas n˜ o necessariamente (b) e (d),
a
dizemos que ela est´ na forma escalonada.
a
Exemplo 1.12. As matrizes
   
1 0 0 1 3 0 2
 0 1 0  e  0 0 1 −3 
0 0 1 0 0 0 0
s˜ o escalonadas reduzidas, enquanto
a
   
1 1 1 1 3 −1 5
 0 −1 2  e  0 0 −5 15 
0 0 5 0 0 0 0
s˜ o escalonadas, mas n˜ o s˜ o escalonadas reduzidas.
a a a
Marco 2012
¸ Reginaldo J. Santos

50. 38 Matrizes e Sistemas Lineares
¸˜ ¸˜
Este m´ todo de resolucao de sistemas, que consiste em aplicar operacoes elemen-
e
`
tares as linhas da matriz aumentada at´ que a matriz do sistema esteja na forma
e
´
escalonada reduzida, e conhecido como m´ todo de Gauss-Jordan.
e
Exemplo 1.13. Considere o seguinte sistema

 x + 3y + 13z = 9
y + 5z = 2
−2y − 10z = −8

´
A sua matriz aumentada e
 
1 3 13 9
 0 1 5 2 
0 −2 −10 −8
1a elimina¸ ao:
. c˜
Como o pivo da 1a linha e igual a 1 e os outros elementos da 1a coluna s˜ o iguais a
ˆ . ´ . a
zero, n˜ o h´ nada o que fazer na 1a eliminacao.
a a . ¸˜
 
1 3 13 9
 0 1 5 2 
 
0 −2 −10 −8
2a elimina¸ ao:
. c˜
Olhamos para submatriz obtida eliminando-se a 1a linha. Escolhemos para pivo um
. ˆ
elemento n˜ o nulo da 1a coluna n˜ o nula da submatriz. Escolhemos o elemento de
a . a
¸˜ ´
posicao 2,2. Como ele e igual a 1, precisamos, agora, “zerar” os outros elementos da
coluna do pivo. Para isto somamos a 1a linha, −3 vezes a 2a e somamos a 3a linha, 2
ˆ ` . . ` .
vezes a 2a .
.
 
−3×2a linha + 1a linha −→ 1a linha
. . . 1 0 −2 3
2×2a linha + 3a linha −→ 3a linha
. . .  0 1 5 2 
0 0 0 −4
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

51. 1.2 ¸˜
Sistemas de Equacoes Lineares 39
´
Portanto o sistema dado e equivalente ao sistema

 x − 2z = 3
y + 5z = 2
0 = −4

¸˜
que n˜ o possui solucao.
a
¸˜ ´
Em geral, um sistema linear n˜ o tem solucao se, e somente se, a ultima linha n˜ o nula
a a
da forma escalonada reduzida da sua matriz aumentada for da forma [ 0 . . . 0 | bm ],
com bm = 0.
Exemplo 1.14. Considere o seguinte sistema

 3z − 9w = 6
5x + 15y − 10z + 40w = −45
x + 3y − z + 5w = −7

´
A sua matriz aumentada e
 
0 0 3 −9 6
 5 15 −10 40 −45 
1 3 −1 5 −7
1a elimina¸ ao:
. c˜
ˆ ˆ
Como temos que “fazer” o pivo igual a um, escolhemos para pivo o elemento de
posicao 3,1. Precisamos “coloc´ -lo” na primeira linha, para isto, trocamos a 3a linha
¸˜ a .
com a 1a .
.
 
a linha ←→ 4a linha
1 3 −1 5 −7
1. .
 5 15 −10 40 −45 
0 0 3 −9 6
Marco 2012
¸ Reginaldo J. Santos

52. 40 Matrizes e Sistemas Lineares
Agora, precisamos “zerar” os outros elementos da 1a coluna, que e a coluna do pivo,
. ´ ˆ
para isto, adicionamos a 2a linha, −5 vezes a 1a .
` . .
 
1 3 −1 5 −7
−5×1a linha + 2a linha −→ 2a linha
. . . 
0 0 −5 15 −10

 
0 0 3 −9 6
2a elimina¸ ao:
. c˜
Olhamos para a sub-matriz obtida eliminando-se a 1a linha. Escolhemos para pivo
. ˆ
um elemento diferente de zero na 1a coluna n˜ o nula desta sub-matriz. Escolhemos
. a
¸˜ ˆ
o elemento de posicao 2,3. Como temos que fazer o pivo igual a 1, multiplicamos a
2a linha por −1/5.
.
 
1 3 −1 5 −7
−(1/5)×2a linha −→ 2a linha
. .  0 0 1 −3 2 
0 0 3 −9 6
Agora, precisamos “zerar” os outros elementos da 2a coluna, que e a coluna do pivo,
. ´ ˆ
`
para isto, adicionamos a 1 a linha a 2a e a 3a linha, −3 vezes a 2a .
. . ` . .
 
a linha + 1a linha −→ 1a linha
. . .
1 3 0 2 −5
2  0 0 1 −3 2 
−3×2a linha + 3a linha −→ 3a linha
. . .
0 0 0 0 0
´ ´
Esta matriz e escalonada reduzida. Portanto o sistema dado e equivalente ao sistema
seguinte
x + 3y + 2w = −5
z − 3w = 2.
ˆ
A matriz deste sistema possui duas colunas sem pivos. As vari´ veis que n˜ o est˜ o
a a a
ˆ ´
associadas a pivos podem ser consideradas vari´ veis livres, isto e, podem assumir
a
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

53. 1.2 ¸˜
Sistemas de Equacoes Lineares 41
valores arbitr´ rios. Neste exemplo as vari´ veis y e w n˜ o est˜ o associadas a pivos
a a a a ˆ
e podem ser consideradas vari´ veis livres. Sejam w = α e y = β. As vari´ veis
a a
associadas aos pivos ter˜ o os seus valores dependentes das vari´ veis livres, z =
ˆ a a
2 + 3α, x = −5 − 2α − 3β. Assim, a solucao geral do sistema e
¸˜ ´
 
 
x −5 − 2α − 3β
 y   β 
 z =
X=    para todos os valores de α e β reais.
2 + 3α 
w α
¸˜
Em geral, se o sistema linear tiver solucao e a forma escalonada reduzida da matriz
ˆ a a a ˆ
aumentada possuir colunas sem pivos, as vari´ veis que n˜ o est˜ o associadas a pivos
a ´
podem ser consideradas vari´ veis livres, isto e, podem assumir valores arbitr´ rios.
a
a ˆ
As vari´ veis associadas aos pivos ter˜ o os seus valores dependentes das vari´ veis
a a
livres.
¸˜ ´
Lembramos que o sistema linear n˜ o tem solucao se a ultima linha n˜ o nula da forma
a a
escalonada reduzida da matriz aumentada do sistema for da forma [ 0 . . . 0 | bm ],
com bm = 0, como no Exemplo 1.13 na p´ gina 38.
a
¸˜ a ´
Observa¸ ao. Para se encontrar a solucao de um sistema linear n˜ o e necess´ rio transformar a matriz aumen-
c˜ a
´
tada do sistema na sua forma escalonada reduzida, mas se a matriz est´ nesta forma, o sistema associado e o
a
ı e e ¸˜
mais simples poss´vel. Um outro m´ todo de resolver sistemas lineares consiste em, atrav´ s da aplicacao de
¸˜ ` ´
operacoes elementares a matriz aumentada do sistema, se chegar a uma matriz que e somente escalonada (isto
´ ¸˜ ¸˜
e, uma matriz que satisfaz as condicoes (a) e (c), mas n˜ o necessariamente (b) e (d) da Definicao 1.6). Este
a
e ´
m´ todo e conhecido como m´ todo de Gauss.
e
Marco 2012
¸ Reginaldo J. Santos

54. 42 Matrizes e Sistemas Lineares
´ ¸˜
O proximo resultado mostra que um sistema linear que tenha mais de uma solucao
´ ¸˜
n˜ o pode ter um numero finito de solucoes.
a
¸˜
Proposicao 1.3. Sejam A uma matriz m × n e B uma matriz m × 1. Se o sistema linear A X = B possui duas solu¸ oes
c˜
distintas X0 = X1 , ent˜ o ele tem infinitas solu¸ oes.
a c˜
¸˜
Demonstracao. Seja
Xλ = (1 − λ) X0 + λX1 , para λ ∈ R.
Vamos mostrar que Xλ e solucao do sistema A X = B, para qualquer λ ∈ R. Para
´ ¸˜
isto vamos mostrar que A Xλ = B.
¸˜
Aplicando as propriedades (i), (j) das operacoes matriciais (Teorema 1.1 na p´ gina 8)
a
obtemos
A Xλ = A[(1 − λ) X0 + λX1 ] = A(1 − λ) X0 + AλX1 = (1 − λ) A X0 + λA X1
Como X0 e X1 s˜ o solucoes de A X = B, ent˜ o A X0 = B e A X1 = B, portanto
a ¸˜ a
A Xλ = (1 − λ) B + λB = [(1 − λ) + λ] B = B,
pela propriedade (f) do Teorema 1.1.
Assim o sistema A X = B tem infinitas solucoes, pois para todo valor de λ ∈ R, Xλ
¸˜
e solucao e Xλ − Xλ = (λ − λ )( X1 − X0 ), ou seja, Xλ = Xλ , para λ = λ .
´ ¸˜
Observe que na demonstracao, para λ = 0, ent˜ o Xλ = X0 , para λ = 1, ent˜ o Xλ = X1 , para λ = 1/2,
¸˜ a a
ent˜ o Xλ = 2 X0 + 1 X1 , para λ = 3, ent˜ o Xλ = −2X0 + 3X1 e para λ = −2, ent˜ o Xλ = 3X0 − 2X1 .
a 1
2 a a
¸˜ ¸˜
No Exemplo 3.4 na p´ gina 153 temos uma interpretacao geom´ trica desta demonstracao.
a e
¸˜ `
Para resolver sistemas lineares vimos aplicando operacoes elementares a matriz au-
mentada do sistema linear. Isto pode ser feito com quaisquer matrizes.
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

55. 1.2 ¸˜
Sistemas de Equacoes Lineares 43
1.2.2 Matrizes Equivalentes por Linhas
¸˜
Definicao 1.7. Uma matriz A = ( aij )m×n e equivalente por linhas a uma matriz B = (bij )m×n , se B pode ser
´
obtida de A aplicando-se uma sequencia de operacoes elementares sobre as suas linhas.
¸˜
Exemplo 1.15. Observando os Exemplos 1.11, 1.14 e 1.13, vemos que as matrizes
     
1 1 1 0 0 3 −9 1 3 13
 2 1 4 ,  5 15 −10 40  ,  0 1 5 
2 3 5 1 3 −1 5 0 −2 −10
`
s˜ o equivalentes por linhas as matrizes
a
     
1 0 0 1 3 0 2 1 0 −2
 0 1 0 ,  0 0 1 −3  ,  0 1 5 ,
0 0 1 0 0 0 0 0 0 0
respectivamente. Matrizes estas que s˜ o escalonadas reduzidas.
a
Cuidado: elas s˜ o equivalentes por linhas, n˜ o s˜ o iguais!
a a a
Marco 2012
¸ Reginaldo J. Santos

56. 44 Matrizes e Sistemas Lineares
¸˜
A relacao “ser equivalente por linhas” satisfaz as seguintes propriedades, cuja
¸˜
verificacao deixamos como exerc´cio para o leitor:
ı
• Toda matriz e equivalente por linhas a ela mesma (reflexividade);
´
• Se A e equivalente por linhas a B, ent˜ o B e equivalente por linhas a A (sime-
´ a ´
tria);
• Se A e equivalente por linhas a B e B e equivalente por linhas a C, ent˜ o A e
´ ´ a ´
equivalente por linhas a C (transitividade).
´
Toda matriz e equivalente por linhas a uma matriz na forma escalonada reduzida e
¸˜
a demonstracao, que omitiremos, pode ser feita da mesma maneira que fizemos no
caso particular das matrizes aumentadas dos Exemplos 1.11, 1.14 e 1.13. No Teorema
´ ´
1.10 na p´ gina 65 mostramos que essa matriz escalonada reduzida e a unica matriz
a
na forma escalonada reduzida equivalente a A.
Teorema 1.4. Toda matriz A = ( aij )m×n e equivalente por linhas a uma unica matriz escalonada reduzida R =
´ ´
(rij )m×n .
´
O proximo resultado ser´ usado para provar alguns resultados no cap´tulo de in-
a ı
vers˜ o de matrizes.
a
¸˜
Proposicao 1.5. Seja R uma matriz n × n, na forma escalonada reduzida. Se R = In , ent˜ o R tem uma linha nula.
a
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

57. 1.2 ¸˜
Sistemas de Equacoes Lineares 45
¸˜
Demonstracao. Observe que o pivo de uma linha i est´ sempre numa coluna j com
ˆ a
j ≥ i. Portanto, ou a ultima linha de R e nula ou o pivo da linha n est´ na posicao
´ ´ ˆ a ¸˜
n, n. Mas, neste caso todas as linhas anteriores s˜ o n˜ o nulas e os pivos de cada linha
a a ˆ
i est´ na coluna i, ou seja, R = In .
a
1.2.3 Sistemas Lineares Homogˆ neos
e
Um sistema linear da forma

 a11 x1 + a12 x2
 + ... + a1n xn = 0
 a21 x1 + a22 x2

+ ... + a2n xn = 0
. . . (1.7)

 .
. .
. = .
.

am1 x1 + am2 x2 + ... + amn xn = 0

´
e chamado sistema homogˆ neo. O sistema (1.7) pode ser escrito 
e ¯
como A X = 0.
  
x1 0
 x2   0 
Todo sistema homogˆ neo admite pelo menos a solucao X =  .  =  .  cha-
e ¸˜
   
 . 
.  . 
.
xn 0
c˜ e ¸˜
mada de solu¸ ao trivial. Portanto, todo sistema homogˆ neo tem solucao. Al´ m
e
¸˜ ¸˜
disso ou tem somente a solucao trivial ou tem infinitas solucoes
Marco 2012
¸ Reginaldo J. Santos

58. 46 Matrizes e Sistemas Lineares
c˜ e ¯
Observa¸ ao. Para resolver um sistema linear homogˆ neo A X = 0, basta escalonarmos a matriz A do sistema,
¸˜ ¸˜ a ´ ´
j´ que sob a acao de uma operacao elementar a coluna de zeros n˜ o e alterada. Mas, e preciso ficar atento
a
` ¸˜
quando se escreve o sistema linear associado a matriz resultante das operacoes elementares, para se levar em
¸˜
consideracao esta coluna de zeros que n˜ o vimos escrevendo.
a
a e ¯
Teorema 1.6. Se A = ( aij )m×n , e tal que m < n, ent˜ o o sistema homogˆneo AX = 0 tem solu¸ ao diferente da solu¸ ao
´ c˜ c˜
trivial, ou seja, todo sistema homogˆneo com menos equa¸ oes do que inc´ gnitas tem infinitas solu¸ oes.
e c˜ o c˜
¸˜
Demonstracao. Como o sistema tem menos equacoes do que incognitas (m < n), o
¸˜ ´
numero de linhas n˜ o nulas r da forma escalonada reduzida da matriz aumentada do
´ a
sistema tamb´ m e tal que r < n. Assim, temos r pivos e n − r vari´ veis (incognitas)
e ´ ˆ a ´
livres, que podem assumir todos os valores reais. Logo, o sistema admite solucao ¸˜
¸˜
n˜ o trivial e portanto infinitas solucoes.
a
¸˜
O conjunto solucao de um sistema linear homogˆ neo satisfaz duas propriedades
e
interessantes.
¸˜
Proposicao 1.7. Seja A = ( aij )m×n .
a c˜ e ¯
(a) Se X e Y s˜ o solu¸ oes do sistema homogˆneo, AX = 0, ent˜ o X + Y tamb´m o e.
a e ´
´ c˜ e ¯
(b) Se X e solu¸ ao do sistema homogˆneo, AX = 0, ent˜ o αX tamb´m o e.
a e ´
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

59. 1.2 ¸˜
Sistemas de Equacoes Lineares 47
¸˜ a ¸˜ e ¯
Demonstracao. (a) Se X e Y s˜ o solucoes do sistema homogˆ neo AX = 0, ent˜ o
a
¯ ¯
AX = 0 e AY = 0 e portanto X + Y tamb´ m e solucao pois, A( X + Y ) =
e ´ ¸˜
¯ ¯
AX + AY = 0 + 0 = 0;¯
´ ¸˜ e ¯
(b) Se X e solucao do sistema homogˆ neo AX = 0, ent˜ o αX tamb´ m o e, pois
a e ´
A(αX ) = αAX = α0 ¯ = 0.
¯
Estas propriedades n˜ o s˜ o v´ lidas para sistemas lineares em geral. Por exemplo,
a a a
considere o sistema linear A X = B, em que A = [1] e B = [1]. A solucao deste
¸˜
sistema e X = [1]. Mas, X + X = 2 X = 2, n˜ o e solucao do sistema.
´ a ´ ¸˜
Exemplo 1.16. Vamos retomar a cadeia de Markov do Exemplo 1.9 na p´ gina 14.
a
¸˜ ´
Vamos supor que uma populacao e dividida em trˆ s estados (por exemplo: ricos,
e
classe m´ dia e pobres) e que em cada unidade de tempo a probabilidade de mudanca
e ¸
´
de um estado para outro seja constante no tempo, so dependa dos estados.
Seja tij a probabilidade de mudanca do estado j para o estado i em uma unidade de
¸
¸˜ ¸˜ ´
tempo (geracao). A matriz de transicao e dada por
 1 2 3 
t11 t12 t13 1
T =  t21 t22 t23  2
t31 t32 t33 3
¸˜
Vamos considerar a matriz de transicao
1 2 3
 1 1 
2 4 0 1
T = 
 1 1 1  2
2 2 2 
0 1 1 3
4 2
Marco 2012
¸ Reginaldo J. Santos

60. 48 Matrizes e Sistemas Lineares
¸˜ ¸˜
Vamos descobrir qual distribuicao inicial da populacao entre os trˆ s estados perma-
e
nece inalterada, geracao apos geracao. Ou seja, vamos determinar P tal que
¸˜ ´ ¸˜
TP = P ou TP = I3 P ou ¯
( T − I3 ) P = 0.
Assim precisamos resolver o sistema linear homogˆ neo
e
 1 1
 −2x
 + 4y = 0
1 1 1
x − 2y + 2z = 0
 2
1 1
4y − 2z = 0

´
cuja matriz aumentada e
 1 1 
−2 4 0 0
1
−1 1
0 
 
 2 2 2
1
0 4 −1
2 0
1a elimina¸ ao:
. c˜
−1
 
1 2 0 0
1
−2×1a linha −→ 2a linha
. . −1 1
0 
 
 2 2 2
1
0 4 −1
2 0
1 −1
 
2 0 0
− 1 × 1a
. linha + 2a
. linha −→ 2a
. linha  0 −1 1
0 
 
2 4 2
1
0 4 −1
2 0
2a elimina¸ ao:
. c˜
−1
 
1 2 0 0
−4×2a linha −→ 2a linha
. .  0 1 −2 0 
1
0 4 −1
2 0
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

61. 1.2 ¸˜
Sistemas de Equacoes Lineares 49
 
1 a a a 1 0 −1 0
2 ×2 linha + 1 linha −→ 1 linha
. . .
1 a linha + 3a linha −→ 3a linha
 0 1 −2 0 
− 4 ×2 . . .
0 0 0 0
´
Portanto o sistema dado e equivalente ao sistema seguinte
x − z = 0
y − 2z = 0
Seja z = α. Ent˜ o y = 2α e x = α. Assim, a solucao geral do sistema e
a ¸˜ ´
   
p1 1
X =  p2  = α  2  , para todo α ∈ R.
p3 1
Tomando a solucao tal que p1 + p2 + p3 = 1 obtemos que se a populacao inicial for
¸˜ ¸˜
distribu´da de forma que p1 = 1/4 da populacao esteja no estado 1, p2 = 1/2 da
ı ¸˜
populacao esteja no estado 2 e p3 = 1/4, esteja no estado 3, ent˜ o esta distribuicao
¸˜ a ¸˜
¸˜ ´ ¸˜
permanecer´ constante geracao apos geracao.
a
1.2.4 Matrizes Elementares (opcional)
¸˜
Definicao 1.8. Uma matriz elementar n × n e uma matriz obtida da matriz identidade In aplicando-se uma, e
´
¸˜
somente uma, operacao elementar.
Vamos denotar por Eij a matriz elementar obtida trocando-se a linha i com a linha
j da matriz In , Ei (α) a matriz elementar obtida multiplicando-se a linha i da matriz
Marco 2012
¸ Reginaldo J. Santos

62. 50 Matrizes e Sistemas Lineares
In pelo escalar α = 0 e Ei,j (α) a matriz elementar obtida da matriz In , somando-se a
`
linha j, α vezes a linha i.
1 0 · · · · · · 0
 
· · · ·
 
1 0 0
 .. 

0 . ·
  .. 


 · 1 ·




 0 . · 


 · 0 ... 1 ·

←i
  · 1 · 
. .
  
Ei,j = 
. .. .

, Ei (α) =  · α · ←i

 · . . . ·

←j  

 · 1 ... 0 ·

  · 1 · 
· 1 ·
   
   .. 

 ..

  · . 0 
 · . 0 
0 · · · · · · 0 1 0 · · · · 0 1
· · · ·
 
1 0 0
 .. 

 0 . · 


 · 1 · ←i

e Ei,j (α) = 
 .
. .. 
· . . · 
· ← j
 

 · α ... 1 
 .. 
 · . 0 
0 · · · · 0 1
Exemplo 1.17. As matrizes seguintes s˜ o as matrizes elementares 2 × 2:
a
0 1 α 0 1 0
E1,2 = E2,1 = , E1 (α) = , E2 (α) = , com α = 0,
1 0 0 1 0 α
1 0 1 α
E1,2 (α) = e E2,1 (α) = .
α 1 0 1
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

63. 1.2 ¸˜
Sistemas de Equacoes Lineares 51
     
1 0 0
 0   1   0 
Sejam E1 =   , E2 =  ,. . . , En =   matrizes m × 1.
     
.
. .
. .
.
 .   .   . 
0 0 1
As matrizes elementares podem ser escritas em termos das matrizes Ei como
E1
 t  
E1 t 
 .  t  .
 .  .

. E1 
 .


 t 
 Ej   .  
Eit

←i  .  ←i
 . 
 
.
 
Ei,j =  . 
. , Ei (α) =  αEit  ← i e Ei,j (α) =  .
   
 .   t . t
  
 Et  ← j  .   E + αE ← j

 i   . 
.  j i 
 .  t .
 .  Em .
 
.  . 
Emt t
Em
¸˜
Aplicar uma operacao elementar em uma matriz, corresponde a multiplicar a matriz
`
a esquerda por uma matriz elementar, como mostra o resultado a seguir.
Teorema 1.8. Sejam E uma matriz elementar m × m e A uma matriz qualquer m × n. Ent˜ o, EA e igual a matriz
a ´ `
obtida aplicando-se na matriz A a mesma opera¸ ao elementar que originou E.
c˜
¸˜
Demonstracao. Como a i-´ sima linha de um produto de matrizes BA e igual a Bi A, em
e ´
que Bi e a i-´ sima linha da matriz B (Exerc´cio 1.1.17 (b) na p´ gina 23) e Eit A = Ai ,
´ e ı a
em que Ai e a linha i da matriz A (Exerc´cio 15 (b) na p´ gina 21), ent˜ o:
´ ı a a
Marco 2012
¸ Reginaldo J. Santos

64. 52 Matrizes e Sistemas Lineares
E1 t   t
E1 A A1
   
 .   .   . 
 . 
.  .  .  . 
 t   t   . 
 Ej   Ej A   Aj 
i →    ←i  ←i
=  . 
 .   . 
Ei,j A =  .  A=  .  .
 
 .   .   . 
j →  Et   Et A  ← j  Ai  ← j
 i   i   
 .   .   . 
 . 
.  .  .  . 
.
Emt t
Em A Am
 t   t   
E1 E1 A A1
 .  .  . 
 .  .  . 
 
 .t  .  . 
 
i →  αEi  A =  αEit A  ← i =  αAi  ← i
 
Ei (α) A =      
 .  .  . 
 .  .  . 
 
.  .  .
Em t t
Em A Am
E1 t t
E1 A A1
     
 .
.   .
.   .
. 
 .   .   . 
Eit Eit A
     
i→ 
  
←i
  Ai ←i

. . .
  
Ei,j (α) A =
 .  A= 
  . 
= 
 . 
 t . t . .
  
j →  E + αE ← j ← j
 t
 E A + αEt A
   
  A j + αAi
 j i   j i   
 .
.
  .
.
  .
.

 .   .   . 
t
Em t
Em A Am
¸˜
Assim, aplicar uma sequencia de operacoes elementares em uma matriz, corres-
`
ponde a multiplicar a matriz a esquerda por um produto de matrizes elementares.
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

65. 1.2 ¸˜
Sistemas de Equacoes Lineares 53
Exemplo 1.18. Quando usamos o m´ todo de Gauss-Jordan para resolver o sistema
e
¸˜
do Exemplo 1.11 na p´ gina 33, aplicamos uma sequencia de operacoes elementares
a
na matriz aumentada do sistema. Isto corresponde a multiplicar a matriz aumentada
 
1 1 1 1000
[ A | B ] =  2 1 4 2000 
2 3 5 2500
a esquerda pelas matrizes elementares
`
   
1 0 0 1 0 0
E1,2 (−2) =  −2 1 0  , E1,3 (−2) =  0 1 0 ,
0 0 1 −2 0 1
     
1 0 0 1 −1 0 1 0 0
E2 (−1) =  0 −1 0  , E2,1 (−1) =  0 1 0  , E2,3 (−1) =  0 1 0 
0 0 1 0 0 1 0 −1 1
     
1 0 0 1 0 −3 1 0 0
E3 ( 1 ) =  0 1 0  , E3,1 (−3) =  0 1
5 0  , E3,2 (2) =  0 1 2 ,
0 0 1
5
0 0 1 0 0 1
ou seja,
 
1 0 0 700
E3,2 (2) E3,1 (−3) E3 ( 1 ) E2,3 (−1) E2,1 (−1) E2 (−1) E1,3 (−2) E1,2 (−2) [ A | B ] =  0 1 0
5 200  .
0 0 1 100
Marco 2012
¸ Reginaldo J. Santos

66. 54 Matrizes e Sistemas Lineares
Exerc´cios Num´ ricos (respostas na p´ gina 517)
ı e a
1.2.1. Quais das seguintes matrizes est˜ o na forma escalonada reduzida:
a
   
1 0 0 0 3 0 1 0 0 −4
A =  0 0 1 0 −4 , B= 0 0 1 0 5 ,
 0 0 0 1 2  0 0 0 −1 2
1 0 0 0 3 0 0 0 0 0
 0 0 1 0 0   0 0 1 2 −4 
C=  0 0 0 1 2 ,
 D= .
 0 0 0 1 0 
0 0 0 0 0 0 0 0 0 0
¸˜
1.2.2. Em cada item suponha que a matriz aumentada de um sistema foi transformada usando operacoes ele-
mentares na matriz escalonada reduzida dada. Resolva o sistema correspondente.
   
1 0 0 −7 8 1 0 0 0 6
(a)  0 1 0 3 2 ; (c)  0 1 0 0 3 ;
0 0 1 1 −5 0 0 1 1 2
   
1 −6 0 0 3 −2 1 7 0 0 −8 −3
 0 0 1 0 4 7   0 0 1 0 6 5 
(b) 
 0
; (d)  .
0 0 1 5 8   0 0 0 1 3 9 
0 0 0 0 0 0 0 0 0 0 0 0
1.2.3. Resolva, usando o m´ todo de Gauss-Jordan, os seguintes sistemas:
e

 x1 + x2 + 2x3 = 8
(a) − x1 − 2x2 + 3x3 = 1 ;
3x1 − 7x2 + 4x3 = 10


 2x1 + 2x2 + 2x3 = 0
(b) −2x1 + 5x2 + 2x3 = 1 ;
8x1 + x2 + 4x3 = −1

Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

67. 1.2 ¸˜
Sistemas de Equacoes Lineares 55

 − 2x2 + 3x3 = 1
(c) 3x1 + 6x2 − 3x3 = −2 .
6x1 + 6x2 + 3x3 = 5

1.2.4. Os sistemas lineares seguintes possuem a mesma matriz A. Resolva-os usando o m´ todo de Gauss-
e
Jordan. Observe que os dois sistemas podem ser resolvidos ao mesmo tempo escalonando a matriz
aumentada [ A | B1 | B2 ].
 
 x1 − 2x2 + x3 = 1  x1 − 2x2 + x3 = 2
(a) 2x1 − 5x2 + x3 = −2 ; (b) 2x1 − 5x2 + x3 = −1 .
3x1 − 7x2 + 2x3 = −1 3x1 − 7x2 + 2x3 = 2
 
 
1 0 5
1.2.5. Seja A =  1 1 1 .
0 1 −4
¯
(a) Encontre a solucao geral do sistema ( A + 4I3 ) X = 0;
¸˜
¯
(b) Encontre a solucao geral do sistema ( A − 2I3 ) X = 0.
¸˜
1.2.6. Para cada sistema linear dado, encontre todos os valores de a para os quais o sistema n˜ o tem solucao,
a ¸˜
¸˜ ´ ¸˜
tem solucao unica e tem infinitas solucoes:

 x + 2y − 3z = 4
(a) 3x − y + 5z = 2 ;
4x + y + ( a2 − 14)z = a + 2


 x + y + z = 2
(b) 2x + 3y + 2z = 5 .
2x + 3y + ( a2 − 1)z = a + 1

´
1.2.7. Uma industria produz trˆ s produtos, X, Y e Z, utilizando dois tipos de insumo, A e B. Para a manufatura
e
de cada kg de X s˜ o utilizados 2 gramas do insumo A e 1 grama do insumo B; para cada kg de Y, 1 grama
a
de insumo A e 3 gramas de insumo B e, para cada kg de Z, 3 gramas de A e 5 gramas de B. O preco de ¸
´
venda do kg de cada um dos produtos X, Y e Z e R$ 3,00, R$ 2,00 e R$ 4,00, respectivamente. Com a venda
Marco 2012
¸ Reginaldo J. Santos

68. 56 Matrizes e Sistemas Lineares
¸˜ ´
de toda a producao de X, Y e Z manufaturada com 1,9 kg de A e 2,4 kg de B, essa industria arrecadou
R$ 2900,00. Determine quantos kg de cada um dos produtos X, Y e Z foram vendidos. (Sugest˜ o: veja o
a
Exemplo 1.11 na p´ gina 33.)
a
1.2.8. Determine os coeficientes a, b, c e d da funcao polinomial p( x ) = ax3 + bx2 + cx + d, cujo gr´ fico passa
¸˜ a
pelos pontos P1 = (0, 10), P2 = (1, 7), P3 = (3, −11) e P4 = (4, −14).
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

69. 1.2 ¸˜
Sistemas de Equacoes Lineares 57
30
y
20
10
0
x
−10
−20
−30
−2 −1 0 1 2 3 4 5
Marco 2012
¸ Reginaldo J. Santos

70. 58 Matrizes e Sistemas Lineares
1.2.9. Determine coeficientes a, b e c da equacao do c´rculo, x2 + y2 + ax + by + c = 0, que passa pelos pontos
¸˜ ı
P1 = (−2, 7), P2 = (−4, 5) e P3 = (4, −3).
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

71. 1.2 ¸˜
Sistemas de Equacoes Lineares 59
y
8
6
4
2
0
x
−2
−4
−6 −4 −2 0 2 4 6 8
Marco 2012
¸ Reginaldo J. Santos

72. 60 Matrizes e Sistemas Lineares
1.2.10. Encontre condicoes sobre os bi ’s para que cada um dos sistemas seja consistente (isto e, tenha solucao):
¸˜ ´ ¸˜
 
 x1 − 2x2 + 5x3 = b1  x1 − 2x2 − x3 = b1
(a) 4x1 − 5x2 + 8x3 = b2 ; (b) −4x1 + 5x2 + 2x3 = b2 .
−3x1 + 3x2 − 3x3 = b3 −4x1 + 7x2 + 4x3 = b3
 
` ¸˜
1.2.11. (Relativo a sub-secao 1.2.4) Considere a matriz
 
0 1 7 8
A= 1 3 3 8 .
−2 −5 1 −8
Encontre matrizes elementares E, F, G e H tais que R = EFGH A e uma matriz escalonada reduzida.
´
(Sugest˜ o: veja o Exemplo 1.18 na p´ gina 53.)
a a
1.2.12. Resolva, usando o m´ todo de Gauss-Jordan, os seguintes sistemas:
e

 x1 + 2x2
 − 3x4 + x5 = 2
x1 + 2x2 + x3 − 3x4 + x5 + 2x6 = 3

(a) ;
 x1 + 2x2
 − 3x4 + 2x5 + x6 = 4
3x1 + 6x2 + x3 − 9x4 + 4x5 + 3x6 = 9


 x1 + 3x2 − 2x3
 + 2x5 = 0
2x1 + 6x2 − 5x3 − 2x4 + 4x5 − 3x6 = −1

(b) ;

 5x3 + 10x4 + 15x6 = 5
2x1 + 6x2 + 8x4 + 4x5 + 18x6 = 6

 
1 1 1 1
 1 3 −2 a 
1.2.13. Considere a matriz A =  ¸˜
 2 2 a − 2 − a − 2 3 a − 1 . Determine o conjunto solucao do sistema

3 a+2 −3 2a+1
t
AX = B, em que B = [ 4 3 1 6 ] , para todos os valores de a.
1.2.14. Resolva os sistemas lineares cujas matrizes aumentadas s˜ o:
a
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

73. 1.2 ¸˜
Sistemas de Equacoes Lineares 61
 
1 2 3 1 8
(a)  1 3 0 1 7 ;
 
1 2 3 0
1 0 2 1 3  1 1 1 0 
(c) 
 1
;
1 2 0 
 
1 1 3 −3 0
(b)  0 2 1 −3 3 ; 1 3 3 0
1 0 2 −1 −1
Exerc´cios usando o M ATLAB
ı
Comandos do M ATLAB :
>> A=[A1,...,An] cria uma matriz A formada pelas matrizes, definidas anteriormente, A1, ..., An
colocadas uma ao lado da outra;
>> expr=subs(expr,x,num) substitui na express˜ o expr a vari´ vel x por num.
a a
>> p=poly2sym([an,...,a0],x) armazena na vari´ vel p o polinomio an x n + . . . + a0 .
a ˆ
>> clf limpa a figura ativa.
Comandos do pacote GAAL:
¸˜
>> B=opel(alpha,i,A) ou >> oe(alpha,i,A)faz a operacao elementar
alpha×linha i ==> linha i da matriz A e armazena a matriz resultante em B.
¸˜
>> B=opel(alpha,i,j,A) ou >> oe(alpha,i,j,A) faz a operacao elementar
alpha×linha i + linha j ==> linha j da matriz A e armazena em B.
>> B=opel(A,i,j) ou >> oe(A,i,j) faz a troca da linha i com a linha j da matriz A e armazena a matriz
resultante em B.
>> B=escalona(A) calcula passo a passo a forma escalonada reduzida da matriz A e armazena a matriz
resultante na vari´ vel B.
a
>> matvand(P,k) obt´ m a matriz de Vandermonde de ordem k, se P=[x1;...;xn] e a matriz de Vander-
e
monde generalizada no caso em que P=[x1,y1;...;xn,yn].
Marco 2012
¸ Reginaldo J. Santos

74. 62 Matrizes e Sistemas Lineares
>> po([x1,y1;x2,y2;...xk,yk]) desenha os pontos (x1,y1),...,(xk,yk).
¸˜ ´
>> plotf1(f,[a,b]) desenha o gr´ fico da funcao dada pela express˜ o simbolica f no intervalo [a,b].
a a
>> plotci(f,[a,b],[c,d]) desenha o gr´ fico da curva dada implicitamente pela express˜ o f(x,y)=0
a a
na regi˜ o do plano [a,b]x[c,d].
a
>> p=poly2sym2([a,b,c,d,e,f],x,y) armazena na vari´ vel p o polinomio em duas vari´ veis ax2 +
a ˆ a
bxy + cy2 + dx + ey + f .
>> eixos desenha os eixos coordenados.
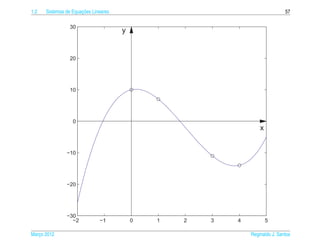
1.2.15. (a) Use o comando P=randi(4,2), para gerar 4 pontos com entradas inteiras e aleatorias entre −5 e 5.
´
Os pontos est˜ o armazenados nas linhas da matriz P.
a
(b) Use o M ATLAB para tentar encontrar os coeficientes a, b, c e d da funcao polinomial p( x ) =
¸˜
ax3 + bx2 + cx + d cujo gr´ fico passa pelos pontos dados pelas linhas da matriz P. A matriz
a
´ ¸˜
A=matvand(P(:,1),3) pode ser util na solucao deste problema, assim como a matriz B=P(:,2).
Se n˜ o conseguiu, repita o passo anterior. Por que pode n˜ o ser poss´vel?
a a ı
ˆ
(c) Desenhe os pontos e o gr´ fico do polinomio com os comandos
a
´
clf, po(P), syms x, p=poly2sym(R(:,5),x), plotf1(p,[-5,5]), em que R e forma escalonada re-
duzida da matriz [A,B].
(d) Desenhe os eixos coordenados com o comando eixos.
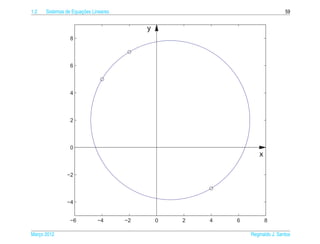
1.2.16. (a) Use o comando P=randi(5,2), para gerar 5 pontos com entradas inteiras e aleatorias entre −5 e 5.
´
Os pontos est˜ o armazenados nas linhas da matriz P.
a
(b) Use o M ATLAB para tentar encontrar os coeficientes a, b, c, d, e e f da conica, curva de equacao
ˆ ¸˜
ax2 + bxy + cy2 + dx + ey + f = 0, cujo gr´ fico passa pelos pontos cujas coordenadas s˜ o dadas
a a
´ ¸˜
pelas linhas da matriz P. A matriz A=matvand(P,2) pode ser util na solucao deste problema. Se n˜ o
a
conseguiu, repita o passo anterior. Por que pode n˜ o ser poss´vel?
a ı
ˆ
(c) Desenhe os pontos e a conica com os comandos
´
clf, po(P), syms x y, p=poly2sym2([-R(:,6);1],x,y), plotci(p,[-5,5],[-5,5]), em que R e a
forma escalonada reduzida da matriz A.
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

75. 1.2 ¸˜
Sistemas de Equacoes Lineares 63
(d) Desenhe os eixos coordenados com o comando eixos.
1.2.17. Use o M ATLAB e resolva os Exerc´cios Num´ ricos a partir do Exerc´cio 1.2.3.
ı e ı
Exerc´cios Teoricos
ı ´
¸˜ ¸˜
1.2.18. Mostre que toda operacao elementar possui inversa, do mesmo tipo, ou seja, para cada operacao elemen-
¸˜ ¸˜
tar existe uma outra operacao elementar do mesmo tipo que desfaz o que a operacao anterior fez.
1.2.19. Prove que:
´
(a) Toda matriz e equivalente por linhas a ela mesma (reflexividade);
(b) Se A e equivalente por linhas a B, ent˜ o B e equivalente por linhas a A (simetria);
´ a ´
(c) Se A e equivalente por linhas a B e B e equivalente por linhas a C, ent˜ o A e equivalente por linhas
´ ´ a ´
a C (transitividade).
1.2.20. e ¯
(a) Sejam X1 e X2 solucoes do sistema homogˆ neo A X = 0. Mostre que αX1 + βX2 e solucao, para
¸˜ ´ ¸˜
quaisquer escalares α e β. (Sugest˜ o: veja o Exemplo 1.7.)
a
(b) Sejam X1 e X2 solucoes do sistema A X = B. Mostre que se αX1 + βX2 e solucao, para quaisquer
¸˜ ´ ¸˜
a ¯
escalares α e β, ent˜ o B = 0. (Sugest˜ o: faca α = β = 0.)
a ¸
¯
1.2.21. Sejam A uma matriz m × n e B = 0 uma matriz m × 1.
(a) Mostre que se X1 e uma solucao do sistema AX = B e Y1 e uma solucao do sistema homogˆ neo
´ ¸˜ ´ ¸˜ e
¯
associado AX = 0, ent˜ o X1 + Y1 e solucao de AX = B.
a ´ ¸˜
(b) Seja X0 solucao particular do sistema AX = B. Mostre que toda solucao X do sistema AX = B, pode
¸˜ ¸˜
ser escrita como X = X0 + Y, em que Y e uma solucao do sistema homogˆ neo associado, AX = 0.
´ ¸˜ e ¯
Assim, a solucao geral do sistema AX = B e a soma de uma solucao particular de AX = B com a
¸˜ ´ ¸˜
¸˜ e ¯
solucao geral do sistema homogˆ neo associado AX = 0. (Sugest˜ o: Escreva X = X0 + ( X − X0 ) e
a
mostre que X − X0 e solucao do sistema homogˆ neo AX = 0.)
´ ¸˜ e ¯
Marco 2012
¸ Reginaldo J. Santos

76. 64 Matrizes e Sistemas Lineares
Apˆ ndice II: Unicidade da Forma Escalonada Reduzida
e
¸˜
Proposicao 1.9. Sejam A e B matrizes m × n equivalentes por linhas. Sejam A1 , . . . , An as colunas 1, . . . , n, respecti-
vamente, da matriz A e B1 , . . . , Bn as colunas 1, . . . , n, respectivamente, da matriz B. Se existem escalares α j1 , . . . , α jk
tais que
Ak = α j1 A j1 + · · · + α jk A jk ,
ent˜ o
a
Bk = α j1 Bj1 + · · · + α jk Bjk ,
¸˜
Demonstracao. Se B e equivalente por linhas a A, ent˜ o B pode ser obtida de A
´ a
¸˜
aplicando-se uma sequencia de operacoes elementares. Aplicar uma operacao ele-¸˜
`
mentar a uma matriz corresponde a multiplicar a matriz a esquerda por uma matriz
invert´vel (Teorema 1.8 na p´ gina 51). Seja M o produto das matrizes invert´veis cor-
ı a ı
respondentes as operacoes elementares aplicadas na matriz A para se obter a matriz
` ¸˜
B. Ent˜ o M e invert´vel e B = MA.
a ´ ı
Sejam α j1 , . . . , α jk escalares tais que
Ak = α j1 A j1 + · · · + α jk A jk ,
ent˜ o multiplicando-se a esquerda pela matriz M obtemos
a `
MAk = α j1 MA j1 + · · · + α jk MA jk .
Como MA j = Bj , para j = 1, . . . , n (Exerc´cio 1.1.17 (a) na p´ gina 23), ent˜ o
ı a a
Bk = α j1 Bj1 + · · · + α jk Bjk .
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

77. 1.2 ¸˜
Sistemas de Equacoes Lineares 65
Teorema 1.10. Se R = (rij )m×n e S = (sij )m×n s˜ o matrizes escalonadas reduzidas equivalentes por linhas a uma
a
matriz A = ( aij )m×n , ent˜ o R = S.
a
¸˜
Demonstracao. Sejam S e R matrizes escalonadas reduzidas equivalentes a A. Sejam
R1 , . . . , Rn as colunas de R e S1 , . . . , Sn as colunas de S. Seja r o numero de linhas
´
n˜ o nulas de R. Sejam j1 , . . . , jr as colunas onde ocorrem os pivos das linhas 1, . . . , r,
a ˆ
respectivamente, da matriz R. Pelo Exerc´cio 19 na p´ gina 63, R e S s˜ o equivalen-
ı a a
¸˜
tes por linha, ou seja, existe uma sequencia de operacoes elementares que podemos
aplicar em R para chegar a S e uma outra sequencia de operacoes elementares que
¸˜
podemos aplicar a S e chegar a R.
Assim, como as colunas 1, . . . , j1 − 1 de R s˜ o nulas o mesmo vale para as colunas
a
1, . . . , j1 − 1 de S. Logo o pivo da 1a linha de S ocorre numa coluna maior ou igual a
ˆ .
j1 . Trocando-se R por S e usando este argumento chegamos a conclus˜ o que R j1 = S j1
a
e assim R1 = S1 , . . . , R j1 = S j1 .
Vamos supor que R1 = S1 , . . . , R jk = S jk e vamos mostrar que
R jk +1 = S jk +1 , . . . , R jk+1 = S jk+1 , se k < r ou
R jr +1 = S jr +1 , . . . , Rn = Sn , se k = r.
Observe que para j = jk + 1, . . . , jk+1 − 1, se k < r, ou para j = jr + 1, . . . , n, se k = r,
temos que
R j = (r1j , . . . , rkj , 0, . . . , 0) = r1j R j1 + . . . + rkj R jk ,
¸˜
o que implica pela Proposicao 1.9 que
S j = r1j S j1 + . . . + rkj S jk .
Mas por hipotese R j1 = S j1 , . . . , R jk = S jk , ent˜ o,
´ a
S j = r1j R j1 + . . . + rkj R jk = R j ,
Marco 2012
¸ Reginaldo J. Santos

78. 66 Matrizes e Sistemas Lineares
para j = jk + 1, . . . , jk+1 − 1, se k < r ou para j = jr + 1, . . . , n, se k = r.
Logo, se k < r, o pivo da (k + 1)-´ sima linha de S ocorre numa coluna maior ou igual
ˆ e
a jk+1 . Trocando-se R por S e usando o argumento anterior chegamos a conclus˜ o a
que R jk+1 = S jk+1 e assim R1 = S1 , . . . , R jr = S jr . E se k = r, ent˜ o R1 = S1 , . . . , Rn =
a
Sn .
Portanto R = S.
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

79. 1.2 ¸˜
Sistemas de Equacoes Lineares 67
Teste do Cap´tulo
ı
1. Para o sistema linear dado, encontre todos os valores de a para os quais o sistema n˜ o tem solucao, tem
a ¸˜
¸˜ ´ ¸˜
solucao unica e tem infinitas solucoes:

 x + 2y + z = 3
x + y − z = 2
x + y + ( a2 − 5) z = a

2. Se poss´vel, encontre os valores de x, y e z tais que:
ı
    
1 2 3 −40 16 x 1 0 0
 2 5 3   13 −5 y = 0 1 0 
1 0 8 5 −2 z 0 0 1
3. Sejam
1 0 cos θ sen θ
D= . e P= .
0 −1 − sen θ cos θ
Sabendo-se que A = Pt DP, calcule D2 , PPt e A2 .
4. Responda Verdadeiro ou Falso, justificando:
(a) Se A2 = −2A4 , ent˜ o ( In + A2 )( In − 2A2 ) = In ;
a
(b) Se A = P t DP, onde D e uma matriz diagonal, ent˜ o At = A;
´ a
(c) Se D e uma matriz diagonal, ent˜ o DA = AD, para toda matriz A, n × n;
´ a
(d) Se B = AAt , ent˜ o B = Bt .
a
(e) Se B e A s˜ o tais que A = At e B = Bt , ent˜ o C = AB, e tal que C t = C.
a a ´
Marco 2012
¸ Reginaldo J. Santos

80. 2
Invers˜ o de Matrizes e Determinantes
a
2.1 Matriz Inversa
Todo numero real a, n˜ o nulo, possui um inverso (multiplicativo), ou seja, existe
´ a
um numero b, tal que a b = b a = 1. Este numero e unico e o denotamos por a−1 .
´ ´ ´ ´
´ ` ´ ´
Apesar da algebra matricial ser semelhante a algebra dos numeros reais, nem todas
as matrizes A n˜ o nulas possuem inversa, ou seja, nem sempre existe uma matriz B
a
tal que A B = B A = In . De in´cio, para que os produtos AB e BA estejam definidos
ı
e sejam iguais e preciso que as matrizes A e B sejam quadradas. Portanto, somente
´
´
as matrizes quadradas podem ter inversa, o que j´ diferencia do caso dos numeros
a
´
reais, pois todo numero n˜ o nulo tem inverso. Mesmo entre as matrizes quadradas,
a
muitas n˜ o possuem inversa, apesar do conjunto das que n˜ o tem inversa ser bem
a a
menor do que o conjunto das que tem (Exerc´cio 2.2.9 na p´ gina 124).
ı a
68

81. 2.1 A Inversa de uma Matriz 69
¸˜
Definicao 2.1. Uma matriz quadrada A = ( aij )n×n e invert´vel ou n˜ o singular, se existe uma matriz B =
´ ı a
(bij )n×n tal que
A B = B A = In , (2.1)
em que In e a matriz identidade. A matriz B e chamada de inversa de A. Se A n˜ o tem inversa, dizemos que
´ ´ a
A e n˜ o invert´vel ou singular.
´ a ı
Exemplo 2.1. Considere as matrizes
−2 1 −1/2 1/6
A= e B= .
0 3 0 1/3
A matriz B e a inversa da matriz A, pois A B = B A = I2 .
´
Teorema 2.1. Se uma matriz A = ( aij )n×n possui inversa, ent˜ o a inversa e unica.
a ´´
Marco 2012
¸ Reginaldo J. Santos

82. 70 Invers˜ o de Matrizes e Determinantes
a
¸˜
Demonstracao. Suponhamos que B e C sejam inversas de A. Ent˜ o, AB = BA = In =
a
AC = CA e assim,
B = B In = B( AC ) = ( BA)C = In C = C .
Denotamos a inversa de A, quando ela existe, por A−1 . Devemos chamar atencao ¸˜
para o fato de que o ´ndice superior −1, aqui, n˜ o significa uma potˆ ncia, t˜ o pouco
ı a e a
uma divis˜ o. Assim como no caso da transposta, em que At significa a transposta de
a
A, aqui, A−1 significa a inversa de A.
2.1.1 Propriedades da Inversa
Teorema 2.2. (a) Se A e invert´vel, ent˜ o A−1 tamb´m o e e
´ ı a e ´
( A −1 ) −1 = A ;
(b) Se A = ( aij )n×n e B = (bij )n×n s˜ o matrizes invert´veis, ent˜ o AB e invert´vel e
a ı a ´ ı
( AB)−1 = B−1 A−1 ;
(c) Se A = ( aij )n×n e invert´vel, ent˜ o At tamb´m e invert´vel e
´ ı a e ´ ı
( A t ) −1 = ( A −1 ) t .
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

83. 2.1 A Inversa de uma Matriz 71
¸˜ ´
Demonstracao. Se queremos mostrar que uma matriz e a inversa de uma outra, temos
`
que mostrar que os produtos das duas matrizes s˜ o iguais a matriz identidade.
a
(a) Uma matriz B e a inversa de A−1 se
´
A−1 B = BA−1 = In .
Mas, como A−1 e a inversa de A, ent˜ o
´ a
AA−1 = A−1 A = In .
Como a inversa e unica, ent˜ o B = A e a inversa de A−1 , ou seja, ( A−1 )−1 = A.
´ ´ a ´
(b) Temos que mostrar que a inversa de AB e B−1 A−1 , ou seja, mostrar que os
´
produtos ( AB)( B−1 A−1 ) e ( B−1 A−1 )( AB) s˜ o iguais a matriz identidade. Mas,
a `
pelas propriedades (h) e (i) do Teorema 1.1 na p´ gina 8:
a
( AB)( B−1 A−1 ) = A( BB−1 ) A−1 = AIn A−1 = AA−1 = In ,
−1 −1 −1 −1 −1 −1
(B A )( AB) = B (A A) B = B In B = B B = In .
(c) Queremos mostrar que a inversa de At e ( A−1 )t . Pela propriedade (o) do Teo-
´
rema 1.1 na p´ gina 8:
a
At ( A−1 )t = ( A−1 A)t = In
t
= In ,
−1 t t −1 t t
(A ) A = ( AA ) = In = In .
Marco 2012
¸ Reginaldo J. Santos

84. 72 Invers˜ o de Matrizes e Determinantes
a
¸˜ ¸˜
O teorema seguinte, cuja demonstracao ser´ omitida no momento (Subsecao 2.1.2),
a
garante que basta verificarmos uma das duas igualdades em (2.1) para sabermos se
´
uma matriz e a inversa de outra.
Teorema 2.3. Sejam A e B matrizes n × n.
(a) Se BA = In , ent˜ o AB = In ;
a
(b) Se AB = In , ent˜ o BA = In ;
a
Assim, para verificar que uma matriz A e invert´vel, quando temos uma matriz B
´ ı
que e candidata a inversa de A, basta fazer um dos produtos AB ou BA e verificar se
´
e igual a In . O proximo exemplo ilustra este fato.
´ ´
¯
Exemplo 2.2. Seja A = ( aij )n×n uma matriz tal que A3 = 0 (A pode n˜ o ser a matriz
a
nula!). Vamos mostrar que a inversa de In − A e In + A + A2 . Para provar isto,
´
devemos multiplicar a matriz In − A, pela matriz que possivelmente seja a inversa
dela, aqui I + A + A2 , e verificar se o produto das duas e igual a matriz identidade
´
In .
( In − A)( In + A + A2 ) = In ( In + A + A2 ) − A( In + A + A2 ) = In + A + A2 − A − A2 − A3 = In .
Aqui foram usadas as propriedades (i) e (j) do Teorema 1.1 na p´ gina 8.
a
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

85. 2.1 A Inversa de uma Matriz 73
2.1.2 Matrizes Elementares e Invers˜ o (opcional)
a
As matrizes elementares tˆ m um papel importante no estudo da invers˜ o de matri-
e a
¸˜
zes e da solucao de sistemas lineares.
¸˜
Proposicao 2.4. Toda matriz elementar e invert´vel e sua inversa e tamb´m uma matriz elementar. Usando a nota¸ ao
´ ı ´ e c˜
introduzida na p´ gina 49, temos:
a
−
(a) Ei,j1 = Ej,i = Ei,j ;
(b) Ei (α)−1 = Ei (1/α), para α = 0;
(c) Ei,j (α)−1 = Ei,j (−α).
¸˜
Demonstracao. Seja E uma matriz elementar. Esta matriz e obtida de In aplicando-
´
se uma operacao elementar. Seja F a matriz elementar correspondente a operacao
¸˜ ¸˜
que transforma E de volta em In . Agora, pelo Teorema 1.8 na p´ gina 51, temos que
a
F E = E F = In . Portanto, F e a inversa de E.
´
Marco 2012
¸ Reginaldo J. Santos

86. 74 Invers˜ o de Matrizes e Determinantes
a
Teorema 2.5. Seja A uma matriz n × n. As seguintes afirma¸ oes s˜ o equivalentes:
c˜ a
(a) Existe uma matriz B, n × n, tal que BA = In .
(b) A matriz A e equivalente por linhas a matriz identidade In .
´ `
(c) A matriz A e invert´vel.
´ ı
¸˜ a ¯
Demonstracao. (a)⇒(b) Se BA = In , ent˜ o o sistema A X = 0 tem somente a
solucao trivial, pois X = In X = BAX = B 0
¸˜ ¯ = 0. Isto implica que a matriz
¯
A e equivalente por linhas a matriz identidade In , pois caso contr´ rio a forma
´ ` a
escalonada reduzida de A teria uma linha nula (Proposicao 1.5 na p´ gina 44).
¸˜ a
(b)⇒(c) A matriz A ser equivalente por linhas a In significa, pelo Teorema 1.8 na
`
p´ gina 51, que existem matrizes elementares E1 , . . . , Ek , tais que
a
Ek . . . E1 A = In (2.2)
−1 −1 − −
( E1 . . . Ek ) Ek . . . E1 A = E1 1 . . . Ek 1
− −
A = E1 1 . . . Ek 1 . (2.3)
a ı ¸˜
Aqui, usamos o fato de que as matrizes elementares s˜ o invert´veis (Proposicao
2.4). Portanto, A e invert´vel como o produto de matrizes invert´veis.
´ ı ı
(c)⇒(a) Claramente.
Se A e invert´vel, ent˜ o multiplicando-se ambos os membros de (2.2) a direita por
´ ı a `
A−1 obtemos
Ek . . . E1 In = A−1 .
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

87. 2.1 A Inversa de uma Matriz 75
Assim, a mesma sequencia de operacoes elementares que transforma a matriz A na
¸˜
matriz identidade In transforma tamb´ m In em A−1 .
e
¸˜ ´
A demonstracao do Teorema 2.3 na p´ gina 72, agora, e uma simples consequˆ ncia
a e
do Teorema anterior.
¸˜
Demonstracao do Teorema 2.3. (a) Vamos mostrar que se BA = In , ent˜ o A e
a ´
invert´vel e B = A−1 . Se BA = In , ent˜ o pelo Teorema 2.5, A e invert´vel e
ı a ´ ı
B = BIn = BAA−1 = In A−1 = A−1 . Logo, AB = BA = In .
(b) Se AB = In , ent˜ o pelo item anterior B e invert´vel e B−1 = A. Portanto BA =
a ´ ı
AB = In .
¸˜ ¸˜
Segue da demonstracao, do Teorema 2.5 (equacao (2.3)) o resultado seguinte.
Teorema 2.6. Uma matriz A e invert´vel se, e somente se, ela e um produto de matrizes elementares.
´ ı ´
Marco 2012
¸ Reginaldo J. Santos

88. 76 Invers˜ o de Matrizes e Determinantes
a
Exemplo 2.3. Vamos escrever a matriz A do Exemplo 2.5 na p´ gina 80 como o pro-
a
duto de matrizes elementares. Quando encontramos a inversa da matriz A, apli-
camos uma sequencia de operacoes elementares em [ A | I3 ] at´ que encontramos
¸˜ e
a matriz [ I3 | A−1 ]. Como as operacoes s˜ o por linha, esta mesma sequencia de
¸˜ a
operacoes elementares transforma A em In . Isto corresponde a multiplicar a matriz
˜
¸ 
1 1 1
A =  2 1 4  a esquerda pelas matrizes elementares
`
2 3 5
   
1 0 0 1 0 0
E1,2 (−2) =  −2 1 0 , E1,3 (−2) =  0 1 0 ,
0 0 1 −2 0 1
     
1 0 0 1 −1 0 1 0 0
E2 (−1) =  0 −1 0  , E2,1 (−1) =  0 1 0 , E2,3 (−1) =  0 1 0 
0 0 1 0 0 1 0 −1 1
     
1 0 0 1 0 −3 1 0 0
1
E3 ( 5 ) =  0 1 0 , E3,1 (−3) =  0 1 0 , E3,2 (2) =  0 1 2 ,
1 0 0 1 0 0 1
0 0 5
ou seja,
E3,2 (2) E3,1 (−3) E3 ( 1 ) E2,3 (−1) E2,1 (−1) E2 (−1) E1,3 (−2) E1,2 (−2) A = I3 .
5
`
Multiplicando a esquerda pelas inversas das matrizes elementares correspondentes
obtemos
A = E1,2 (2) E1,3 (2) E2 (−1) E2,1 (1) E2,3 (1) E3 (5) E3,1 (3) E3,2 (−2).
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

89. 2.1 A Inversa de uma Matriz 77
2.1.3 M´ todo para Invers˜ o de Matrizes
e a
O exemplo seguinte mostra, para matrizes 2 × 2, n˜ o somente uma forma de desco-
a
brir se uma matriz A tem inversa mas tamb´ m, como encontrar a inversa, no caso
e
em que ela exista. Ou seja, escalonamos a matriz [ A | I2 ] e encontramos a sua forma
escalonada reduzida [ R | S]. Se R = I2 , ent˜ o a matriz A e invert´vel e a inversa
a ´ ı
A−1 = S. Caso contr´ rio, a matriz A n˜ o e invert´vel.
a a ´ ı
a b x y
Exemplo 2.4. Seja A = c d
. Devemos procurar uma matriz B =
z w
tal
que AB = I2 , ou seja,

 ax
 + bz = 1
cx + dz = 0


 ay + bw = 0
cy + dw = 1

Este sistema pode ser desacoplado em dois sistemas independentes que possuem a
mesma matriz, que e a matriz A. Podemos resolvˆ -los simultaneamente. Para isto,
´ e
basta escalonarmos a matriz aumentada
a b 1 0
= [ A | I2 ].
c d 0 1
¸˜ ´
Os dois sistemas tˆ m solucao unica se, e somente se, a forma escalonada reduzida
e
1 0 s t
da matriz [ A | I2 ] for da forma [ I2 | S ] = (verifique, observando o
0 1 u v
que acontece se a forma escalonada reduzida da matriz A n˜ o for igual a I2 ). Neste
a
caso, x = s, z = u e y = t, w = v, ou seja, a matriz A possuir´ inversa, A−1 = B =
a
s t
S= .
u v
Marco 2012
¸ Reginaldo J. Santos

90. 78 Invers˜ o de Matrizes e Determinantes
a
¸˜ ´ ´
Para os leitores da Subsecao 2.1.2 o proximo teorema e uma simples consequˆ ncia do
e
¸˜
Teorema 2.5 na p´ gina 74. Entretanto a demonstracao que daremos a seguir fornece
a
um m´ todo para encontrar a inversa de uma matriz, se ela existir.
e
Teorema 2.7. Uma matriz A, n × n, e invert´vel se, e somente se, A e equivalente por linhas a matriz identidade In .
´ ı ´ `
¸˜
Demonstracao. Pelo Teorema 2.3 na p´ gina 72, para verificarmos se uma matriz A,
a
n × n, e invert´vel, basta verificarmos se existe uma matriz B, tal que
´ ı
A B = In . (2.4)
Vamos denotar as colunas de B por X1 , X2 , . . . , Xn , ou seja, B = [ X1 . . . Xn ], em que
     
x11 x12 x1n
 x21   x22   x2n 
X1 =  .  , X2 =  .  , . . . , X n =  . 
     
 . 
.  .  .  . 
.
xn1 xn2 xnn
e as colunas da matriz identidade In , por E1 , E2 , . . . , En , ou seja, In = [ E1 . . . En ], em
que      
1 0 0
 0   1   0 
E1 =  .  , E2 =  .  , . . . , En =  .  .
     
 . 
.  . 
.  . 
.
0 0 1
¸˜
Assim a equacao (2.4) pode ser escrita como
A [ X1 . . . Xn ] = [ AX1 . . . AXn ] = [ E1 . . . En ],
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

91. 2.1 A Inversa de uma Matriz 79
pois a j-´ sima coluna do produto AB e igual a A vezes a j-´ sima coluna da matriz B
e ´ e
ı a ¸˜
(Exerc´cio 17 na p´ gina 23). Analisando coluna a coluna a equacao anterior vemos
que encontrar B e equivalente a resolver n sistemas lineares
´
A X j = Ej para j = 1 . . . , n.
Cada um dos sistemas pode ser resolvido usando o m´ todo de Gauss-Jordan. Para
e
isso, formar´amos as matrizes aumentadas [ A | E1 ], [ A | E2 ], . . . , [ A | En ]. Entre-
ı
tanto, como as matrizes dos sistemas s˜ o todas iguais a A, podemos resolver todos
a `
os sistemas simultaneamente formando a matriz n × 2n
[ A | E1 E2 . . . En ] = [ A | In ].
Transformando [ A | In ] na sua forma escalonada reduzida, que vamos denotar por
[ R | S ], vamos chegar a duas situacoes poss´veis: ou a matriz R e a matriz identi-
¸˜ ı ´
a ´
dade, ou n˜ o e.
• Se R = In , ent˜ o a forma escalonada reduzida da matriz [ A | In ] e da
a ´
forma [ In | S ]. Se escrevemos a matriz S em termos das suas colunas S =
[ S1 S2 . . . Sn ], ent˜ o as solucoes dos sistemas A X j = Ej s˜ o X j = S j e assim
a ¸˜ a
B = S e tal que A B = In e pelo Teorema 2.3 na p´ gina 72 A e invert´vel.
´ a ´ ı
• Se R = In , ent˜ o a matriz A n˜ o e equivalente por linhas a matriz identidade
a a ´ `
In . Ent˜ o, pela Proposicao 1.5 na p´ gina 44 a matriz R tem uma linha nula. O
a ¸˜ a
que implica que cada um dos sistemas A X j = Ej ou n˜ o tem solucao unica ou
a ¸˜ ´
n˜ o tem solucao. Isto implica que a matriz A n˜ o tem inversa, pois as colunas
a ¸˜ a
da (unica) inversa seriam X j , para j = 1, . . . n.
´
Observa¸ ao. Da demonstracao do Teorema 2.7 obtemos n˜ o somente uma forma de descobrir se uma matriz A
c˜ ¸˜ a
tem inversa mas tamb´ m, como encontrar a inversa, no caso em que ela exista. Ou seja, escalonamos a matriz
e
[ A | In ] e encontramos a sua forma escalonada reduzida [ R | S]. Se R = In , ent˜ o a matriz A e invert´vel e a
a ´ ı
inversa A−1 = S. Caso contr´ rio, a matriz A n˜ o e invert´vel. Vejamos os exemplos seguintes.
a a ´ ı
Marco 2012
¸ Reginaldo J. Santos

92. 80 Invers˜ o de Matrizes e Determinantes
a
Exemplo 2.5. Vamos encontrar, se existir, a inversa de
 
1 1 1
A= 2 1 4 
2 3 5
1a elimina¸ ao:
. c˜
 
1 1 1 1 0 0
−2×1a linha + 2a linha −→ 2a linha
. . .
 0 −1 2 −2 1 0 
−2×1a linha + 3a linha −→ 3a linha
. . .
0 1 3 −2 0 1
2a elimina¸ ao:
. c˜
 
1 1 1 1 0 0
− 1 × 2a
. linha −→ 2a
. linha  0 1 −2 2 −1 0 
0 1 3 −2 0 1
 
−1×2a linha + 1a linha −→ 1a linha
. . . 1 0 3 −1 1 0
−1×2a linha + 3a linha −→ 3a linha
. . .  0 1 −2 2 −1 0 
0 0 5 −4 1 1
3a elimina¸ ao:
. c˜
 
1 0 3 −1 1 0
1 a
5 ×3
. linha −→ 3a linha
.  0 1 −2 2 −1 0 
0 0 1 −4
5
1
5
1
5
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

93. 2.1 A Inversa de uma Matriz 81
7 2
−3
 
1 0 0 5 5 5
−3×3a linha + 1a linha −→ 1a linha
. . . 2
 0 1 0 −3 2
 
2×3a linha + 2a linha −→ 2a linha
. . . 5 5 5 
0 0 1 −4
5
1
5
1
5
Assim, a matriz [ A | I3 ] e equivalente por linhas a matriz acima, que e da forma
´ ` ´
[ I3 | S], portanto a matriz A e invert´vel e a sua inversa e a matriz S, ou seja,
´ ı ´
7 2
−3
 
5 5 5
A −1 =  2
−3 2
.
 
5 5 5
−4
5
1
5
1
5
Exemplo 2.6. Vamos determinar, se existir, a inversa da matriz
 
1 2 3
A= 1 1 2 .
0 1 1
Para isso devemos escalonar a matriz aumentada
 
1 2 3 1 0 0
[ A | I3 ] =  1 1 2 0 1 0 
0 1 1 0 0 1
1a elimina¸ ao:
. c˜
 
1 2 3 1 0 0
−1×1a linha + 2a linha −→ 2a linha
. . .  0 1 1 1 −1 0 
0 1 1 0 0 1
Marco 2012
¸ Reginaldo J. Santos

94. 82 Invers˜ o de Matrizes e Determinantes
a
2a elimina¸ ao:
. c˜
 
1 2 3 1 0 0
−1×2a linha −→ 2a linha
. .  0 1 1 1 −1 0 
0 1 1 0 0 1
 
1 0 1 −1 2 0
−2×2a linha + 1a linha −→ 1a linha
. . .
a linha + 3a linha −→ 3a linha
 0 1 1 1 −1 0 
−1×2 . . .
0 0 0 −1 1 1
Assim, a matriz [ A | I3 ] e equivalente por linhas a matriz acima, que e da forma
´ ` ´
[ R | S], com R = I3 . Assim, a matriz A n˜ o e equivalente por linhas a matriz identi-
a ´ `
a ´
dade e portanto n˜ o e invert´vel.
ı
Se um sistema linear A X = B tem o numero de equa¸ oes igual ao numero de
´ c˜ ´
incognitas, ent˜ o o conhecimento da inversa da matriz do sistema A−1 , reduz o
´ a
problema de resolver o sistema a simplesmente fazer um produto de matrizes, como
´
est´ enunciado no proximo teorema.
a
Teorema 2.8. Seja A uma matriz n × n.
(a) O sistema associado AX = B tem solu¸ ao unica se, e somente se, A e invert´vel. Neste caso a solu¸ ao e X = A−1 B;
c˜ ´ ´ ı c˜ ´
¯
(b) O sistema homogˆneo A X = 0 tem solu¸ ao n˜ o trivial se, e somente se, A e singular (n˜ o invert´vel).
e c˜ a ´ a ı
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

95. 2.1 A Inversa de uma Matriz 83
Demonstracao. (a) Se a matriz A e invert´vel, ent˜ o multiplicando A X = B por A−1
¸˜ ´ ı a
`
a esquerda em ambos os membros obtemos
A −1 ( A X ) = A −1 B
( A −1 A ) X = A −1 B
In X = A −1 B
X = A−1 B.
Aqui foram usadas as propriedades (h) e (i) do Teorema 1.1 na p´ gina 8. Por-
a
tanto, X = A−1 B e a unica solucao do sistema A X = B. Por outro lado, se o
´ ´ ¸˜
sistema A X = B possui solucao unica, ent˜ o a forma escalonada reduzida da
¸˜ ´ a
matriz aumentada do sistema [ A | B] e da forma [ R | S], em que R = In . Pois a
´
matriz A e quadrada e caso R fosse diferente da identidade possuiria uma linha
´
de zeros (Proposicao 1.5 na p´ gina 44) o que levaria a que o sistema A X = B ou
¸˜ a
n˜ o tivesse solucao ou tivesse infinitas solucoes. Logo, a matriz A e equivalente
a ¸˜ ¸˜ ´
`
por linhas a matriz identidade o que pelo Teorema 2.7 na p´ gina 78 implica que
a
A e invert´vel.
´ ı
¸˜
(b) Todo sistema homogˆ neo possui pelo menos a solucao trivial. Pelo item ante-
e
rior, esta ser´ a unica solucao se, e somente se, A e invert´vel.
a ´ ¸˜ ´ ı
´
Vamos ver no proximo exemplo que se conhecemos a inversa de uma matriz,
a ¸˜ ´
ent˜ o a producao de uma industria em v´ rios per´odos pode ser obtida apenas
a ı
¸˜
multiplicando-se a inversa por matrizes colunas que contenham a arrecadacao e as
quantidades dos insumos utilizados em cada per´odo.
ı
Exemplo 2.7. Uma industria produz trˆ s produtos, X, Y e Z, utilizando dois tipos de
´ e
insumo, A e B. Para a manufatura de cada kg de X s˜ o utilizados 1 grama do insumo
a
A e 2 gramas do insumo B; para cada kg de Y, 1 grama de insumo A e 1 grama de
insumo B e, para cada kg de Z, 1 grama de A e 4 gramas de B. O preco de venda do
¸
´
kg de cada um dos produtos X, Y e Z e R$ 2,00, R$ 3,00 e R$ 5,00, respectivamente.
Marco 2012
¸ Reginaldo J. Santos

96. 84 Invers˜ o de Matrizes e Determinantes
a
¸˜
Como vimos no Exemplo 1.6 na p´ gina 6, usando matrizes o esquema de producao
a
pode ser descrito da seguinte forma:
X Y Z  
gramas de A/kg 1 1 1 x kg de X produzidos
gramas de B/kg  2 1 4  = A X=  y  kg de Y produzidos
preco/kg
¸ 2 3 5 z kg de Z produzidos
 
x+y+z gramas de A usados
AX =  2x + y + 4z  gramas de B usados
2x + 3y + 5z ¸˜
arrecadacao
No Exemplo 2.5 na p´ gina 80 determinamos a inversa da matriz
a
 
1 1 1
A= 2 1 4 
2 3 5
´
que e
7 2
−3
   
5 5 5 7 −3
2
1
A −1 =  2
−3 2
 =  2 −3 2 .
  
5 5 5 5
−4
5
1
5
1
5
−4 1 1
Sabendo-se a inversa da matriz A podemos saber a producao da industria sempre
¸˜ ´
¸˜
que soubermos quanto foi gasto do insumo A, do insumo B e a arrecadacao.
¸˜
(a) Se em um per´odo com a venda de toda a producao de X, Y e Z manufaturada
ı
´
com 1 kg de A e 2 kg de B, essa industria arrecadou R$ 2500, 00, ent˜ o para
a
determinar quantos kg de cada um dos produtos X, Y e Z foram vendidos sim-
plesmente multiplicamos A−1 pela matriz
 
1000 gramas de A usados
B =  2000  gramas de B usados
2500 ¸˜
arrecadacao
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

97. 2.1 A Inversa de uma Matriz 85
ou seja,
 
kg de X produzidos

x
 7 2−3  1000   700 
kg de Y produzidos  y  = X = A −1 B = 1  2 −3 2   2000  =  200 

5

kg de Z produzidos z −4 1 1 2500 100
Portanto, foram produzidos 700 kg do produto X, 200 kg de Y e 100 kg de Z.
¸˜
(b) Se em outro per´odo com a venda de toda a producao de X, Y e Z manufatu-
ı
´
rada com 1 kg de A e 2, 1 kg de B, essa industria arrecadou R$ 2900, 00, ent˜ o
a
para determinar quantos kg de cada um dos produtos X, Y e Z foram vendidos
simplesmente multiplicamos A−1 pela matriz
 
1000 gramas de A usados
B =  2100  gramas de B usados
2900 ¸˜
arrecadacao
ou seja,
 
kg de X produzidos

x
 7 2−3  1000   500 
kg de Y produzidos  y  = X = A −1 B = 1  2 −3 2   2100  =  300 

5

kg de Z produzidos z −4 1 1 2900 200
Portanto, foram produzidos 500 kg do produto X, 300 kg de Y e 200 kg de Z.
Vamos mostrar a rec´proca do item (b) do Teorema 2.2 na p´ gina 70. Este resultado
ı a
a´ ¸˜ ´
ser´ util na demonstracao de que o determinante do produto de matrizes e o produto
¸˜
dos determinantes (Subsecao 2.2.2 na p´ gina 112).
a
Marco 2012
¸ Reginaldo J. Santos

98. 86 Invers˜ o de Matrizes e Determinantes
a
¸˜
Proposicao 2.9. Se A e B s˜ o matrizes n × n, com AB invert´vel, ent˜ o A e B s˜ o invert´veis.
a ı a a ı
¸˜ ¯
Demonstracao. Considere o sistema ( AB) X = 0. Se B n˜ o fosse invert´vel, ent˜ o exis-
a ı a
tiria X = 0,¯ tal que B X = 0 (Teorema 2.8 na p´ gina 82). Multiplicando-se por A,
¯ a
ı ¯
ter´amos AB X = 0, o que, novamente pelo Teorema 2.8 na p´ gina 82, contradiz o
a
fato de AB ser invert´vel. Portanto, B e invert´vel. Agora, se B e AB s˜ o invert´veis,
ı ´ ı a ı
ent˜ o A tamb´ m e invert´vel, pois A = ( AB) B−1 , que e o produto de duas matrizes
a e ´ ı ´
invert´veis.
ı
¸˜ ¸˜
2.1.4 Aplicacao: Interpolacao Polinomial
Sejam P1 = ( x1 , y1 ), . . . , Pn = ( xn , yn ), com x1 , . . . , xn numeros distintos. Considere
´
o problema de encontrar um polinomio de grau n − 1
ˆ
p ( x ) = a n −1 x n −1 + a n −2 x n −2 + · · · + a 1 x + a 0 ,
que interpola os dados, no sentido de que p( xi ) = yi , para i = 1, . . . , n.
Por exemplo se os pontos s˜ o P1 = (0, 10), P2 = (1, 7), P3 = (3, −11), P4 = (4, −14)
a
ˆ
ent˜ o o problema consiste em encontrar um polinomio de grau 3 que interpola os
a
pontos dados (veja o Exerc´cio 1.2.8 na p´ gina 56).
ı a
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

99. 2.1 A Inversa de uma Matriz 87
30
y
20
10
0
x
−10
−20
−30
−2 −1 0 1 2 3 4 5
ˆ
Vamos mostrar que existe, um e somente um, polinomio de grau no m´ ximo igual
a
a n − 1, que interpola n pontos, com abscissas distintas. Substituindo os pontos no
Marco 2012
¸ Reginaldo J. Santos

100. 88 Invers˜ o de Matrizes e Determinantes
a
polinomio p( x ), obtemos um sistema linear AX = B, em que
ˆ
 n −1
x 1 −2
n
    
a n −1 y1 x1 ... x1 1
 a n −2   y2   x n −1 x n −2 ... x2 1 
 2 2
X =  . , B =  .  e A =  . .
    
 .   .   . .
. .
.
. . . . . 
a0 yn x n −1
n x n −2
n ... xn 1
A matriz A e chamada matriz de Vandermonde.
´
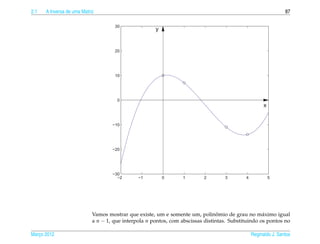
Vamos mostrar que AX = B tem somente uma solucao. Pelo Teorema 2.8 na p´ gina
¸˜ a
82, um sistema de n equacoes e n incognitas AX = B tem solucao unica se, e somente
¸˜ ´ ¸˜ ´
e ¯
se, o sistema homogˆ neo associado, AX = 0, tem somente a solucao trivial. X =
¸˜
[ an−1 · · · a0 ] e solucao do sistema homogˆ neo se, e somente se, o polinomio de
´ ¸˜ e ˆ
grau n − 1, p( x ) = an−1 x n−1 + · · · + a0 , se anula em n pontos distintos. O que
implica que o polinomio p( x ) e o polinomio com todos os seus coeficientes iguais a
ˆ ´ ˆ
e ¯
zero. Portanto, o sistema homogˆ neo A X = 0 tem somente a solucao trivial. Isto
¸˜
prova que existe, um e somente um, polinomio de grau no m´ ximo igual a n − 1,
ˆ a
que interpola n pontos, com abscissas distintas.
Assim a solucao do sistema linear e X = A−1 B. Como a matriz A depende apenas
¸˜ ´
das abscissas dos pontos, tendo calculado a matriz A−1 podemos determinar rapi-
ˆ
damente os polinomios que interpolam v´ rios conjuntos de pontos, desde que os
a
pontos de todos os conjuntos tenham as mesmas abscissas dos pontos do conjunto
inicial.
¸˜
2.1.5 Aplicacao: Criptografia
Vamos transformar uma mensagem em uma matriz da seguinte forma. Vamos que-
brar a mensagem em pedacos de tamanho 3 e cada pedaco ser´ convertido em uma
¸ ¸ a
´
matriz coluna usando a Tabela 2.1 de convers˜ o entre caracteres e numeros.
a
Considere a seguinte mensagem criptografada
1ydobbr,? (2.5)
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

101. 2.1 A Inversa de uma Matriz 89
a b c d e f g h i j k l m n
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
o p q r s t u v w x y z a
` a
´ a
^
15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
a
~ c
¸ e
´ e
^ ı
´ o
´ o
^ o
~ u
´ u
¨ A B C D E
30 31 32 33 34 35 36 37 38 39 40 41 42 43 44
F G H I J K L M N O P Q R S T
45 46 47 48 49 50 51 52 53 54 55 56 57 58 59
U V W X Y Z `
A ´
A ^
A ~
A ¸
C ´
E ^
E ´
I ´
O
60 61 62 63 64 65 66 67 68 69 70 71 72 73 74
^
O ~
O ´
U ¨
U 0 1 2 3 4 5 6 7 8 9 :
75 76 77 78 79 80 81 82 83 84 85 86 87 88 89
; < = > ? @ ! " # $ % & ’ ( )
90 91 92 93 94 95 96 97 98 99 100 101 102 103 104
* + , - . / [ ] _ { | }
105 106 107 108 109 110 111 112 113 114 115 116 117
´
Tabela 2.1 – Tabela de convers˜ o de caracteres em numeros
a
Quebrando a mensagem criptografada em pedacos de tamanho 3 e convertendo
¸
´
cada pedaco para uma coluna de numeros usando a Tabela 2.1 obtemos a matriz
¸
 
80 15 18
Y =  25 2 107 
4 2 94
Sabendo-se que esta mensagem foi criptografada fazendo o produto da mensagem
Marco 2012
¸ Reginaldo J. Santos

102. 90 Invers˜ o de Matrizes e Determinantes
a
inicial pela matriz  
1 1 0
M= 0 1 1 
0 0 1
ent˜ o
a
X = M −1 Y
´
ser´ a mensagem inicial convertida para numeros, ou seja,
a
    
1 −1 1 80 15 18 59 15 5
X = M −1 Y =  0 1 −1   25 2 107  =  21 0 13 
0 0 1 4 2 94 4 2 94
Convertendo para texto usando novamente a Tabela 2.1 obtemos que a mensagem
´
que foi criptografada e
Tudo bem? (2.6)
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

103. 2.1 A Inversa de uma Matriz 91
Exerc´cios Num´ ricos (respostas na p´ gina 539)
ı e a

1
´ ¸˜ e ¯
2.1.1. Seja A uma matriz 3 × 3. Suponha que X =  −2  e solucao do sistema homogˆ neo A X = 0. A matriz
3
A e singular ou n˜ o? Justifique.
´ a
2.1.2. Se poss´vel, encontre as inversas das seguintes matrizes:
ı
   
1 2 3 1 2 3
(a)  1 1 2 ; (d)  0 2 3 ;
0 1 2 1 2 4
   
1 2 2 1 2 3
(b)  1 3 1 ; (e)  1 1 2 ;
1 3 2 0 1 1
   
1 1 1 1 1 1 1 1
 1 2 −1 2   1 3 1 2 
(c) 
 1 −1
; (f)  ;
2 1   1 2 −1 1 
1 3 3 2 5 9 1 6
 
1 1 0
2.1.3. Encontre todos os valores de a para os quais a matriz A =  1 0 0  tem inversa.
1 2 a
2.1.4. Se
3 2 2 5
A −1 = e B −1 = ,
1 3 3 −2
encontre ( A B)−1 .
2 3 5
2.1.5. Resolva o sistema A X = B, se A−1 = eB= .
4 1 3
Marco 2012
¸ Reginaldo J. Santos

104. 92 Invers˜ o de Matrizes e Determinantes
a
2.1.6. (Relativo a Subsecao 2.1.2) Encontre matrizes elementares E1 , . . . , Ek tais que A = E1 . . . Ek , para
` ¸˜
 
1 2 3
A =  2 1 2 .
0 1 2
Exerc´cios usando o M ATLAB
ı
Comandos do M ATLAB :
`
>> M=[A,B] atribui a matriz M a matriz obtida colocando lado a lado as matrizes A e B.
>> A=[A1,...,An] cria uma matriz A formada pelas matrizes, definidas anteriormente, A1, ..., An
colocadas uma ao lado da outra;
` `
>> M=A(:,k:l) atribui a matriz M a submatriz da matriz A obtida da coluna l a coluna k da matriz A.
Comando do pacote GAAL:
>> B=escalona(A) calcula passo a passo a forma escalonada reduzida da matriz A e armazena a matriz
resultante na vari´ vel B.
a
2.1.7. O pacote GAAL cont´ m alguns arquivos com mensagens criptografadas e uma chave para decifr´ -las. Use
e a
`
os comandos a seguir para ler dos arquivos e atribuir as vari´ veis correspondentes, uma mensagem crip-
a
tografada e a uma chave para decifr´ -la.
a
>> menc=lerarq(’c:/matlab/toolbox/gaal/menc1.txt’)
>> key=lerarq(’c:/matlab/toolbox/gaal/key.txt’)
ı `
Com estes comandos foram lidos os arquivos menc1.txt e key.txt e atribu´dos os resultados as vari´ veis
a
menc e key respectivamente. Para converter a mensagem criptografada e a chave para matrizes num´ ricas
e
use os comandos do pacote gaal:
>> y=char2num(menc), M=char2num(key)
´
Sabendo-se que a mensagem criptografada (convertida para numeros), y, foi originalmente obtida
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

105. 2.1 A Inversa de uma Matriz 93
´
multiplicando-se a matriz M pela mensagem original (convertida para numeros), x, determine x. Des-
cubra a mensagem usando o comando do pacote gaal, num2char(x), que converte a matriz para texto.
Decifre as mensagens que est˜ o nos arquivos menc2.txt e menc3.txt. Como deve ser a matriz M para
a
que ela possa ser uma matriz chave na criptografia?
Exerc´cios Teoricos
ı ´
a b
2.1.8. (a) Mostre que a matriz A = e invert´vel se, e somente se, ad − bc = 0 e neste caso a inversa
´ ı
c d
´
e dada por
1 d −b
A −1 = .
ad − bc −c a
(Sugest˜ o: encontre a forma escalonada reduzida da matriz [ A | I2 ], para a = 0 e para a = 0.)
a
(b) Mostre que se ad − bc = 0, ent˜ o o sistema linear
a
ax + by = g
cx + dy = h
¸˜
tem como solucao
gd − bh ah − gc
x= , y=
ad − bc ad − bc
Sugest˜ o para os proximos 4 exerc´cios: Para verificar que uma matriz B e a inversa de uma matriz A,
a ´ ı ´
basta fazer um dos produtos AB ou BA e verificar que e igual a In .
´
¯
2.1.9. Se A e uma matriz n × n e Ak = 0, para k um inteiro positivo, mostre que
´
( In − A)−1 = In + A + A2 + . . . + Ak−1 .
2.1.10. Seja A uma matriz diagonal, isto e, os elementos que est˜ o fora da diagonal s˜ o iguais a zero (aij = 0,
´ a a
para i = j). Se aii = 0, para i = 1, . . . , n, mostre que A e invert´vel e a sua inversa e tamb´ m uma matriz
´ ı ´ e
diagonal com elementos na diagonal dados por 1/a11 , 1/a22 , . . . , 1/ann .
Marco 2012
¸ Reginaldo J. Santos

106. 94 Invers˜ o de Matrizes e Determinantes
a
2.1.11. Sejam A e B matrizes quadradas. Mostre que se A + B e A forem invert´veis, ent˜ o
ı a
( A + B)−1 = A−1 ( In + BA−1 )−1 .
2.1.12. Seja Jn a matriz n × n, cujas entradas s˜ o iguais a 1. Mostre que se n > 1, ent˜ o
a a
1
( In − Jn )−1 = In − Jn .
n−1
2
(Sugest˜ o: observe que Jn = nJn .)
a
2.1.13. Mostre que se B e uma matriz invert´vel, ent˜ o AB−1 = B−1 A se, e somente se, AB = BA. (Sugest˜ o:
´ ı a a
multiplique a equacao AB = BA por B−1 .)
¸˜
2.1.14. Mostre que se A e uma matriz invert´vel, ent˜ o A + B e In + BA−1 s˜ o ambas invert´veis ou ambas n˜ o
´ ı a a ı a
invert´veis. (Sugest˜ o: multiplique A + B por A−1 .)
ı a
2.1.15. Sejam A e B matrizes n × n. Mostre que se B n˜ o e invert´vel, ent˜ o AB tamb´ m n˜ o o e.
a ´ ı a e a ´
2.1.16. Mostre que se A e B s˜ o matrizes n × n, invert´veis, ent˜ o A e B s˜ o equivalentes por linhas.
a ı a a
2.1.17. Sejam A uma matriz m × n e B uma matriz n × m, com n < m. Mostre que AB n˜ o e invert´vel. (Sugest˜ o:
a ´ ı a
¯
Mostre que o sistema ( AB) X = 0 tem solucao n˜ o trivial.)
¸˜ a
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

107. 2.2 Determinantes 95
2.2 Determinantes
Vamos inicialmente definir o determinante de matrizes 1 × 1. Para cada matriz A =
[ a] definimos o determinante de A, indicado por det( A), por det( A) = a. Vamos,
agora, definir o determinante de matrizes 2 × 2 e a partir da´ definir para matrizes
ı
de ordem maior. A cada matriz A, 2 × 2, associamos um numero real, denominado
´
determinante de A, por:
a11 a12
det( A) = det = a11 a22 − a12 a21 .
a21 a22
Para definir o determinante de matrizes quadradas maiores, precisamos definir o
que s˜ o os menores de uma matriz. Dada uma matriz A = ( aij )n×n , o menor do ele-
a
˜ ´
mento aij , denotado por Aij , e a submatriz (n − 1) × (n − 1) de A obtida eliminando-
se a i-´ sima linha e a j-´ sima coluna de A, que tem o seguinte aspecto:
e e
 j 
a11 ... ... a1n
 
 .
. .
.

. .
 
 
 
 
 
˜
Aij = 

aij

 i
 
 
 .
. .
.

. .
 
 
 
 
an1 ... ... ann
Marco 2012
¸ Reginaldo J. Santos

108. 96 Invers˜ o de Matrizes e Determinantes
a
Exemplo 2.8. Para uma matriz A = ( aij )3×3 ,
 
a11 a12 a13
a11 a12
 
˜
A23 =  a21

a22 a23 =

  a31 a32
a31 a32 a33
Agora, vamos definir os cofatores de uma matriz quadrada A = ( aij )3×3 . O cofator
˜ ´
do elemento aij , denotado por aij , e definido por
aij = (−1)i+ j det( Aij ),
˜ ˜
˜
ou seja, o cofator aij , do elemento aij e igual a mais ou menos o determinante do
´
menor A ˜ ij , sendo o mais e o menos determinados pela seguinte disposicao:
¸˜
 
+ − +
 − + − 
+ − +
Exemplo 2.9. Para uma matriz A = ( aij )3×3 ,
 
a11 a12 a13
a11 a12
 
a23 = (−1)2+3 det( A23 ) = −det  a21
˜ ˜ a22 a23  = −det = a31 a12 − a11 a32
 
  a31 a32
a31 a32 a33
Vamos, agora, definir o determinante de uma matriz 3 × 3. Se
 
a11 a12 a13
A= a ,
 
21 a22 a23
a31 a32 a33
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

109. 2.2 Determinantes 97
ent˜ o, o determinante de A e igual a soma dos produtos dos elementos da 1a linha
a ´ ` .
pelos seus cofatores.
det( A) ˜ ˜ ˜
= a11 a11 + a12 a12 + a13 a13
a22 a23 a21 a23 a21 a22
= a11 det − a12 det + a13 det
a32 a33 a31 a33 a31 a32
= a11 ( a22 a33 − a32 a23 ) − a12 ( a21 a33 − a31 a23 ) + a13 ( a21 a32 − a31 a22 ).
Da mesma forma que a partir do determinante de matrizes 2 × 2, definimos o deter-
minante de matrizes 3 × 3, podemos definir o determinante de matrizes quadradas
de ordem maior. Supondo que sabemos como calcular o determinante de matrizes
(n − 1) × (n − 1) vamos definir o determinante de matrizes n × n.
Vamos definir, agora, os cofatores de uma matriz quadrada A = ( aij )n×n . O cofator
˜ ´
do elemento aij , denotado por aij , e definido por
aij = (−1)i+ j det( Aij ),
˜ ˜
˜
ou seja, o cofator aij , do elemento aij e igual a mais ou menos o determinante do
´
menor A ˜ ij , sendo o mais e o menos determinados pela seguinte disposicao:
¸˜
 
+ − + − ...
 − + − + ... 
 
 + − + − ... 
. . . ..
 
. . . ..
. . . . .
¸˜
Definicao 2.2. Seja A = ( aij )n×n . O determinante de A, denotado por det( A), e definido por
´
n
˜ ˜ ˜
det( A) = a11 a11 + a12 a12 + . . . + a1n a1n = ∑ a1j a1j ,
˜ (2.7)
j =1
Marco 2012
¸ Reginaldo J. Santos

110. 98 Invers˜ o de Matrizes e Determinantes
a
˜
em que a1j = (−1)1+ j det( A1j ) e o cofator do elemento a1j . A express˜ o (2.8) e chamada desenvolvimento em
˜ ´ a ´
cofatores do determinante de A em termos da 1a linha.
.
Exemplo 2.10. Seja  
0 0 0 −3
 
A=
 1 2 3 4 .

 −1 3 2 5 
2 1 −2 0
Desenvolvendo-se o determinante de A em cofatores, obtemos
 
1 2 3
det( A) = 0a11 + 0a12 + 0a13 + (−3)(−1)1+4 det( B),
˜ ˜ ˜ em que B= .
 
−1 3 2
2 1 −2
Mas o det( B) tamb´ m pode ser calculado usando cofatores,
e
det( B) ˜ ˜ ˜
= 1b11 + 2b12 + 3b13
= 1(−1)1+1 det( B11 ) + 2(−1)1+2 det( B12 ) + 3(−1)1+3 det( B13 )
˜ ˜ ˜
32 −1 2 −1 3
= det − 2 det + 3 det
−2
1 2 −2 2 1
= −8 − 2 (−2) + 3 (−7)
= −25
Portanto,
det( A) = 3 det( B) = −75.
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

111. 2.2 Determinantes 99
Exemplo 2.11. Usando a definicao de determinante, vamos mostrar que o determi-
¸˜
´
nante de uma matriz triangular inferior (isto e, os elementos situados acima da dia-
´
gonal principal s˜ o iguais a zero) e o produto dos elementos da diagonal principal.
a
Vamos mostrar inicialmente para matrizes 3 × 3. Seja
 
a11 0 0
A= a
 
21 a22 0 
a31 a32 a33
Desenvolvendo-se o determinante de A em cofatores, obtemos
a22 0
det( A) = a11 det = a11 a22 a33 .
a32 a33
Vamos supor termos provado que para qualquer matriz (n − 1) × (n − 1) triangular
´
inferior, o determinante e o produto dos elementos da diagonal principal. Ent˜ o
a
vamos provar que isto tamb´ m vale para matrizes n × n. Seja
e
 
a11 0 . . . . . . 0
 
 . 
. 
 a21 a22 0 . 
A=
 .
. .. 
 . . 0 
an1 ... ann
Desenvolvendo-se o determinante de A em cofatores, obtemos
 
a22 0 . . . . . . 0
 . 
. 
 a a33 0 . 
det( A) = a11 det  32
 .  = a11 a22 . . . ann ,
. ..
 . . 0 
an2 ... ann
Marco 2012
¸ Reginaldo J. Santos

112. 100 Invers˜ o de Matrizes e Determinantes
a
pois o determinante acima e de uma matriz (n − 1) × (n − 1) triangular inferior. Em
´
particular, para a matriz identidade, In ,
det( In ) = 1.
2.2.1 Propriedades do Determinante
Vamos provar uma propriedade importante do determinante. Para isso vamos es-
crever a matriz A = ( aij )n×n em termos das suas linhas
 
A1
 .
. 

 . 

 A k −1 
 
A =  Ak

,

 A k +1 
 
 .
 .

. 
An
em que Ai e a linha i da matriz A, ou seja, Ai = [ ai1 ai2 . . . ain ]. Se a linha Ak e
´ ´
escrita na forma Ak = αX + βY, em que X = [ x1 . . . xn ], Y = [ y1 . . . yn ] e α e β
s˜ o escalares, dizemos que a linha Ak e combina¸ ao linear de X e Y. Se a linha Ak
a ´ c˜
e combinacao linear de X e Y, ent˜ o o determinante pode ser decomposto como no
´ ¸˜ a
resultado seguinte.
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

113. 2.2 Determinantes 101
Teorema 2.10. Seja A = ( aij )n×n escrita em termos das suas linhas, denotadas por Ai , ou seja,
Ai = [ ai1 ai2 . . . ain ]. Se para algum k, a linha Ak = αX + βY, em que X = [ x1 . . . xn ],
Y = [ y1 . . . yn ] e α e β s˜ o escalares, ent˜ o:
a a
     
A1 A1 A1
.
.  .   .
 .   .
  

 . 
  .   .


 A k −1   A k −1   A k −1 
     
 αX + βY  = α det  X  + β det  Y
det  .
    
 A k +1   A k +1   A k +1 
     
.
.
 .   .
 .   .
  
 .  . . 
An An An
Aqui, Ak = αX + βY = [ αx1 + βy1 . . . αxn + βyn ].
¸˜
Demonstracao. Vamos provar aqui somente para k = 1. Para k > 1 e demonstrado ´
no Apˆ ndice III na p´ gina 127. Se A1 = αX + βY, em que X = [ x1 . . . xn ], Y =
e a
[ y1 . . . yn ] e α e β s˜ o escalares, ent˜ o:
a a
 
αX + βY
 A2  n
det   = ∑ (−1)1+ j (αx j + βy j ) det( A1j )
˜
 
.
.
 .  j =1
An
n n
= α ∑ x j det( A1j ) + β ∑ y j det( A1j )
˜ ˜
j =1 j =1
   
X Y
 A2   A2 
= α det   + β det 
   
.
. .
. 
 .   . 
An An
Marco 2012
¸ Reginaldo J. Santos

114. 102 Invers˜ o de Matrizes e Determinantes
a
Exemplo 2.12. O c´ lculo do determinante da matriz a seguir pode ser feito da se-
a
guinte forma:
cos t sen t cos t sen t cos t sen t
det = 2 det + 3 det =3
2 cos t − 3 sen t 2 sen t + 3 cos t cos t sen t − sen t cos t
¸˜
Pela definicao de determinante, o determinante deve ser calculado fazendo-se o de-
senvolvimento em cofatores segundo a 1a linha. O proximo resultado, que n˜ o va-
. ´ a
mos provar neste momento (Apˆ ndice III na p´ gina 127), afirma que o determinante
e a
pode ser calculado fazendo-se o desenvolvimento em cofatores segundo qualquer li-
nha ou qualquer coluna.
Teorema 2.11. Seja A uma matriz n × n. O determinante de A pode ser calculado fazendo-se o desenvolvimento em
cofatores segundo qualquer linha ou qualquer coluna.
n
det( A) ˜ ˜ ˜
= ai1 ai1 + ai2 ai2 + . . . + ain ain = ∑ aij aij ,
˜ para i = 1, . . . , n, (2.8)
j =1
n
˜ ˜ ˜
= a1j a1j + a2j a2j + . . . + anj anj = ∑ aij aij ,
˜ para j = 1, . . . , n, (2.9)
i =1
˜ ˜ ´
em que aij = (−1)i+ j det( Aij ) e o cofator do elemento aij . A express˜ o (2.8) e chamada desenvolvimento em co-
a ´
fatores do determinante de A em termos da i-´ sima linha e (2.9) e chamada desenvolvimento em cofatores do
e ´
determinante de A em termos da j-´ sima coluna.
e
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

115. 2.2 Determinantes 103
Temos a seguinte consequˆ ncia deste resultado.
e
Corol´ rio 2.12. Seja A uma matriz n × n. Se A possui duas linhas iguais, ent˜ o det( A) = 0.
a a
Demonstracao. O resultado e claramente verdadeiro para matrizes 2 × 2. Supondo que
¸˜ ´
o resultado seja verdadeiro para matrizes (n − 1) × (n − 1), vamos provar que ele e
´
verdadeiro para matrizes n × n. Suponhamos que as linhas k e l sejam iguais, para
k = l. Desenvolvendo o determinante de A em termos de uma linha i, com i = k, l,
obtemos
n n
det( A) = ∑ aij aij = ∑ (−1)i+ j aij det( Aij ).
˜ ˜
j =1 j =1
˜ ´
Mas, cada Aij e uma matriz (n − 1) × (n − 1) com duas linhas iguais. Como estamos
˜
supondo que o resultado seja verdadeiro para estas matrizes, ent˜ o det( Aij ) = 0.
a
Isto implica que det( A) = 0.
Marco 2012
¸ Reginaldo J. Santos

116. 104 Invers˜ o de Matrizes e Determinantes
a
´
No proximo resultado mostramos como varia o determinante de uma matriz quando
¸˜
aplicamos operacoes elementares sobre suas linhas.
Teorema 2.13. Sejam A e B matrizes n × n.
(a) Se B e obtida de A multiplicando-se uma linha por um escalar α, ent˜ o
´ a
det( B) = α det( A) ;
(b) Se B resulta de A pela troca da posi¸ ao de duas linhas k = l, ent˜ o
c˜ a
det( B) = − det( A) ;
(c) Se B e obtida de A substituindo a linha l por ela somada a um multiplo escalar de uma linha k, k = l, ent˜ o
´ ´ a
det( B) = det( A) .
¸˜
Demonstracao. (a) Segue diretamente do Teorema 2.10 na p´ gina 100.
a
(b) Sejam
   
A1 A1
 .   . 
 .   . 
 .   . 
 Ak   Al 
   
A= .  B =  . .
 .   . 
e
 .   . 
 Al   Ak 
   
 .   . 
 ..   .. 
An An
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

117. 2.2 Determinantes 105
Agora, pelo Teorema 2.10 na p´ gina 100 e o Corol´ rio 2.12, temos que
a a
         
A1 A1 A1 A1 A1
.
.  .   .   .   . 
 .   .   .   . 
 

 . 
  .   .   .   . 
 Ak + Al   Ak   Ak   Al   Al 
         
.
.  .   .   .   . 
0 = det   = det  .  + det  .  + det  .  + det  . 
 
 .   .   .   .   . 
 Ak + Al   Ak   Al   Ak   Al 
         
 .
.
  . 
 . 
 . 
 . 
 . 
 . 
 . 
 . 
 .  . . . .
An An An An An
= 0 + det( A) + det( B) + 0.
Portanto, det( A) = − det( B).
(c) Novamente, pelo Teorema 2.10 na p´ gina 100, temos que
a
       
A1 A1 A1 A1
.
.  .   .   . 
 .   .   . 
 

 . 
  .   .   . 

 Ak 

 Ak 
 
 Ak 
 
 Ak 
 
.
.  .   .   . 
det   = det  .  + α det  .  = det  .  .
 
 .   .   .   . 
 Al + αAk   Al   Ak   Al 
       
 .
.
  . 
 . 
 . 
 . 
 . 
 . 
 .  . . .
An An An An
Exemplo 2.13. Vamos calcular o determinante da matriz
 
0 1 5
A= 3 −6 9 
2 6 1
Marco 2012
¸ Reginaldo J. Santos

118. 106 Invers˜ o de Matrizes e Determinantes
a
¸˜
usando operacoes elementares para transform´ -la numa matriz triangular superior
a
e aplicando o Teorema 2.13.
 
3 −6 9
det( A) = − det  0 1 5  1a linha ←→ 2a linha
. .
 2 6 1 
1 −2 3
= −3 det  0 1 5  1/3×1a linha −→ 1a linha
. .
 2 6 1 
1 −2 3
= −3 det  0 1 5  −2×1a linha+3a linha −→ 3a linha
. . .
 0 10 −5 
1 −2 3
= −3 det  0 1 5  −10×2a linha+3a linha −→ 3a linha
. . .
0 0 −55
= (−3)(−55) = 165
Quando multiplicamos uma linha de uma matriz por um escalar α o determinante
´
da nova matriz e igual a α multiplicado pelo determinante da matriz antiga. Mas o
´ ´
que estamos calculando aqui e o determinante da matriz antiga, por isso ele e igual
a 1/α multiplicado pelo determinante da matriz nova.
Para se calcular o determinante de uma matriz n × n pela expans˜ o em cofatores, pre-
a
cisamos fazer n produtos e calcular n determinantes de matrizes (n − 1) × (n − 1),
que por sua vez vai precisar de n − 1 produtos e assim por diante. Portanto, ao todo
s˜ o necess´ rios da ordem de n! produtos. Para se calcular o determinante de uma
a a
matriz 20 × 20, e necess´ rio se realizar 20! ≈ 1018 produtos. Os computadores pes-
´ a
soais realizam da ordem de 108 produtos por segundo. Portanto, um computador
pessoal precisaria de cerca de 1010 segundos ou 103 anos para calcular o determi-
nante de uma matriz 20 × 20 usando a expans˜ o em cofatores. Entretanto usando
a
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

119. 2.2 Determinantes 107
e a ´
o m´ todo apresentado no exemplo anterior para o c´ lculo do determinante, e ne-
cess´ rio apenas da ordem de n3 produtos. Ou seja, para calcular o determinante de
a
uma matriz 20 × 20 usando o m´ todo apresentado no exemplo anterior um compu-
e
tador pessoal gasta muito menos de um segundo.
A seguir estabelecemos duas propriedades do determinante que ser˜ o demonstradas
a
¸˜
somente na Subsecao 2.2.2 na p´ gina 112.
a
Teorema 2.14. Sejam A e B matrizes n × n.
(a) Os determinantes de A e de sua transposta At s˜ o iguais,
a
det( A) = det( At ) ;
(b) O determinante do produto de A por B e igual ao produto dos seus determinantes,
´
det( AB) = det( A) det( B) .
Marco 2012
¸ Reginaldo J. Santos

120. 108 Invers˜ o de Matrizes e Determinantes
a
´
Observa¸ ao. Como o determinante de uma matriz e igual ao determinante da sua transposta (Teorema 2.14
c˜
¸˜ `
(b)), segue-se que todas as propriedades que se referem a linhas s˜ o v´ lidas com relacao as colunas.
a a
Exemplo 2.14. Seja A = ( aij )n×n . Vamos mostrar que se A e invert´vel, ent˜ o
´ ı a
1
det( A−1 ) = .
det( A)
Como A A−1 = In , aplicando-se o determinante a ambos os membros desta igual-
dade e usando o Teorema 2.14, obtemos
det( A) det( A−1 ) = det( In ).
Mas, det( In ) = 1 (Exemplo 2.11 na p´ gina 99, a matriz identidade tamb´ m e trian-
a e ´
−1 1
gular inferior!). Logo, det( A ) = .
det( A)
Exemplo 2.15. Se uma matriz quadrada e tal que A2 = A−1 , ent˜ o vamos mostrar
´ a
que det( A) = 1. Aplicando-se o determinante a ambos os membros da igualdade
acima, e usando novamente o Teorema 2.14 e o resultado do exemplo anterior, obte-
mos
1
(det( A))2 = .
det( A)
Logo, (det( A))3 = 1. Portanto, det( A) = 1.
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

121. 2.2 Determinantes 109
O resultado seguinte caracteriza em termos do determinante as matrizes invert´veis
ı
¸˜ a
e os sistemas lineares homogˆ neos que possuem solucao n˜ o trivial.
e
Teorema 2.15. Seja A uma matriz n × n.
(a) A matriz A e invert´vel se, e somente se, det( A) = 0.
´ ı
e ¯
(b) O sistema homogˆneo AX = 0 tem solu¸ ao n˜ o trivial se, e somente se, det( A) = 0.
c˜ a
¸˜
Demonstracao. (a) Seja R a forma escalonada reduzida da matriz A.
¸˜ ¸˜
A demonstracao deste item segue-se de trˆ s observacoes:
e
• Pelo Teorema 2.13 na p´ gina 104, det( A) = 0 se, e somente se, det( R) = 0.
a
• Pela Proposicao 1.5 da p´ gina 44, ou R = In ou a matriz R tem uma linha
¸˜ a
nula. Assim, det( A) = 0 se, e somente se, R = In .
• Pelo Teorema 2.7 na p´ gina 78, R = In se, e somente se, A e invert´vel.
a ´ ı
a e ¯
(b) Pelo Teorema 2.8 na p´ gina 82, o sistema homogˆ neo AX = 0 tem solucao n˜ o
¸˜ a
trivial se, e somente se, a matriz A n˜ o e invert´vel. E pelo item anterior, a
a ´ ı
matriz A e n˜ o invert´vel se, e somente se, det( A) = 0.
´ a ı
Exemplo 2.16. Considere a matriz
 
2 2 2
A= 0 2 0 .
0 1 3
Marco 2012
¸ Reginaldo J. Santos

122. 110 Invers˜ o de Matrizes e Determinantes
a
 
x
¯
(a) Determinar os valores de λ ∈ R tais que existe X =  y  = 0 que satisfaz
z
AX = λX.
(b) Para 
cada  dos valores de λ encontrados no item anterior determinar todos
um
x
¯
X =  y  = 0 tais que AX = λX.
z
Solu¸ ao:
c˜
(a) Como a matriz identidade I3 e o elemento neutro do produto, ent˜ o
´ a
AX = λX ⇔ AX = λI3 X.
Subtraindo-se λI3 X obtemos
¯
AX − λI3 X = 0 ⇔ ¯
( A − λI3 ) X = 0.
e ¸˜ a ¯
Agora, este sistema homogˆ neo tem solucao n˜ o trivial (X = 0) se, e somente
se,
det( A − λI3 ) = 0.
Mas  
2−λ 2 2
det  0 2−λ 0  = −(λ − 2)2 (λ − 3) = 0
0 1 3−λ
se, e somente se, λ = 2 ou λ = 3. Assim, somente para λ = 2 e λ = 3 existem
 
x
¯
vetores X =  y  = 0 tais que AX = λX.
z
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

123. 2.2 Determinantes 111
(b) Para λ = 2:
    
0 2
2 x 0
¯ 2y + 2z = 0
( A − 2I3 ) X = 0 ⇔  0 0  y  =  0  ⇔
0
y + z = 0
0 1
1 z 0
   
x β
que tem solucao o conjunto dos X =  y  =  −α , para todos os valores
¸˜
z α
de α, β ∈ R.
Para λ = 3:
     
−1 2 2 x 0  − x + 2y + 2z = 0
¯
( A − 3I3 ) X = 0 ⇔  0 −1 0   y  =  0  ⇔ −y = 0
0 1 0 z 0 y = 0

   
x 2α
que tem solucao o conjunto dos X =  y  =  0 , para todos os valores
¸˜
z α
de α ∈ R.
a b
Exemplo 2.17. A matriz A = c d
e invert´vel se, e somente se, det( A) = ad −
´ ı
bc = 0. Neste caso a inversa de A e dada por
´
1 d −b
A −1 = ,
det( A) −c a
como pode ser verificado multiplicando-se a candidata a inversa pela matriz A.
Observe que este exemplo fornece uma regra para se encontrar a inversa de uma
matriz 2 × 2: troca-se a posicao dos elementos da diagonal principal, troca-se o sinal
¸˜
dos outros elementos e divide-se todos os elementos pelo determinante de A.
Marco 2012
¸ Reginaldo J. Santos

124. 112 Invers˜ o de Matrizes e Determinantes
a
Exemplo 2.18. Considere o sistema linear de 2 equacoes e 2 incognitas
¸˜ ´
ax + by = g
cx + dy = h
´
A matriz deste sistema e
a b
A= .
c d
Se det( A) = 0, ent˜ o a solucao do sistema e
a ¸˜ ´
 
g b
1 d −b g 1 dg − bh 1  det h d
X = A −1 B =

= =  
det( A) −c a h det( A) −cg + ah det( A)  a g 
det
c h
ou seja,
g b a g
det det
h d c h
x= , y=
a b a b
det det
c d c d
´ ¸˜ ´
esta e a chamada Regra de Cramer para sistemas de 2 equacoes e 2 incognitas.A
Regra de Cramer para sistemas de n equacoes e n incognitas ser´ apresentada na
¸˜ ´ a
¸˜
Subsecao 2.2.3.
2.2.2 Matrizes Elementares e o Determinante (opcional)
´
Relembramos que uma matriz elementar e uma matriz que se obt´ m aplicando-se
e
¸˜
uma operacao elementar na matriz identidade. Assim, aplicando-se o Teorema 2.13
na p´ gina 104 obtemos o resultado seguinte.
a
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

125. 2.2 Determinantes 113
¸˜
Proposicao 2.16. (a) Se Ei,j e a matriz elementar obtida trocando-se as linhas i e j da matriz identidade, ent˜ o
´ a
det( Ei,j ) = −1.
(b) Se Ei (α) e a matriz elementar obtida da matriz identidade, multiplicando-se a linha i por α, ent˜ o
´ a
det( Ei (α)) = α.
(c) Se Ei,j (α) e a matriz elementar obtida da matriz identidade, somando-se a linha j, α vezes a linha i, ent˜ o
´ ` a
det( Ei,j (α)) = 1.
Marco 2012
¸ Reginaldo J. Santos

126. 114 Invers˜ o de Matrizes e Determinantes
a
´ ´
Lembramos tamb´ m que uma matriz e invert´vel se, e somente se, ela e o produto
e ı
de matrizes elementares (Teorema 2.6 na p´ gina 75). Al´ m disso, o resultado da
a e
¸˜ ¸˜ ´
aplicacao de uma operacao elementar em uma matriz e o mesmo que multiplicar a
`
matriz a esquerda pela matriz elementar correspondente.
Usando matrizes elementares podemos provar o Teorema 2.14 na p´ gina 107.
a
¸˜
Demonstracao do Teorema 2.14.
(a) Queremos provar que det( AB) = det( A) det( B). Vamos dividir a demonstracao
¸˜
deste item em trˆ s casos:
e
Caso 1: Se A = E e uma matriz elementar. Este caso segue-se diretamente da
´
¸˜
proposicao anterior e do Teorema 2.13 na p´ gina 104.
a
Caso 2: Se A e invert´vel, ent˜ o pelo Teorema 2.6 na p´ gina 75 ela e o produto de
´ ı a a ´
matrizes elementares, A = E1 . . . Ek . Aplicando-se o caso anterior sucessivas vezes,
obtemos
det( AB) = det( E1 ) . . . det( Ek ) det( B) = det( E1 . . . Ek ) det( B) = det( A) det( B).
Caso 3: Se A e singular, pela Proposicao 2.9 na p´ gina 86, AB tamb´ m e singular.
´ ¸˜ a e ´
Logo,
det( AB) = 0 = 0 det( B) = det( A) det( B).
(b) Queremos provar que det( A) = det( At ). Vamos dividir a demonstracao deste
¸˜
item em dois casos.
Caso 1: Se A e uma matriz invert´vel, pelo Teorema 2.6 na p´ gina 75 ela e o produto
´ ı a ´
´ a
de matrizes elementares, A = E1 . . . Ek . E f´ cil ver que se E e uma matriz elementar,
´
ent˜ o det( E) = det( Et ) (verifique!). Assim,
a
det( At ) = det( Ek ) . . . det( E1 ) = det( Ek ) . . . det( E1 ) = det( E1 . . . Ek ) = det( A).
t t
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

127. 2.2 Determinantes 115
Caso 2: Se A n˜ o e invert´vel, ent˜ o At tamb´ m n˜ o o e, pois caso contr´ rio, pelo
a ´ ı a e a ´ a
Teorema 2.2 na p´ gina 70, tamb´ m A = ( At )t seria invert´vel. Assim neste caso,
a e ı
det( At ) = 0 = det( A).
2.2.3 Matriz Adjunta e Invers˜ o (opcional)
a
Vamos definir a adjunta de uma matriz quadrada e em seguida enunciar e provar um
teorema sobre a adjunta que permite provar v´ rios resultados sobre matrizes, entre
a
´
eles um que fornece uma formula para a inversa de uma matriz e tamb´ m a regra de
e
Cramer. Tanto a adjunta quanto os resultados que vem a seguir s˜ o de importˆ ncia
a a
´
teorica.
¸˜
Definicao 2.3. Seja A uma matriz n × n. Definimos a matriz adjunta (cl´ ssica) de A, denotada por adj( A),
a
como a transposta da matriz formada pelos cofatores de A, ou seja,
 t  
˜
a11 ˜
a12 ... ˜
a1n ˜
a11 ˜
a21 ... ˜
an1
 ˜
a21 ˜
a22 ... ˜
a2n   ˜
a12 ˜
a22 ... ˜
an2 
adj( A) =   = ,
   
.
. .
. .
. .
.
 . ... .   . ... . 
˜
an1 ˜
an2 ... ˜
ann ˜
a1n ˜
a2n ... ˜
ann
˜ ´
em que, aij = (−1)i+ j det( Aij ) e o cofator do elemento aij , para i, j = 1, . . . , n.
˜
Marco 2012
¸ Reginaldo J. Santos

128. 116 Invers˜ o de Matrizes e Determinantes
a
Exemplo 2.19. Seja  
1 2 3
B= 0 3 2 .
0 0 −2
Vamos calcular a adjunta de B.
˜ 3 2 ˜ 0 2
b11 = (−1)1+1 det = −6, b12 = (−1)1+2 det = 0,
0 −2 0 −2
˜ 0 3 ˜ 2 3
b13 = (−1)1+3 det = 0, b21 = (−1)2+1 det = 4,
0 0 0 −2
˜ 1 3 ˜ 1 2
b22 = (−1)2+2 det = −2, b23 = (−1)2+3 det = 0,
0 −2 0 0
˜ 2 3 ˜ 1 3
b31 = (−1)3+1 det = −5, b32 = (−1)3+2 det = −2,
3 2 0 2
˜ 1 2
b33 = (−1)3+3 det = 3,
0 3
Assim, a adjunta de B e
´
 t  
−6 0 0 −6 4 −5
adj( B) =  4 −2 0  =  0 −2 −2 
−5 −2 3 0 0 3
¸˜
Na definicao do determinante s˜ o multiplicados os elementos de uma linha pelos
a
cofatores da mesma linha. O teorema seguinte diz o que acontece se somamos os
produtos dos elementos de uma linha com os cofatores de outra linha ou se somamos
os produtos dos elementos de uma coluna com os cofatores de outra coluna.
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

129. 2.2 Determinantes 117
Lema 2.17. Se A e uma matriz n × n, ent˜ o
´ a
˜ ˜ ˜
ak1 ai1 + ak2 ai2 + . . . + akn ain = 0 se k = i; (2.10)
˜ ˜ ˜
a1k a1j + a2k a2j + . . . + ank anj = 0 se k = j; (2.11)
˜ ´
em que, aij = (−1)i+ j det( Aij ) e o cofator do elemento aij , para i, j = 1, . . . , n.
˜
Demonstracao. Para demonstrar a equacao (2.10), definimos a matriz A∗ como sendo a
¸˜ ¸˜
matriz obtida de A substituindo a i-´ sima linha de A por sua k-´ sima linha, ou seja,
e e
   
A1 A1
 .   . 
 .   . 
 .   . 
 Ai   Ak 
 ←i  ←i
 . 
A=  .  e A∗ =  . 
 . 
.
 .   . 
 Ak  ← k  Ak  ← k
   
 .   . 
 . 
.  . 
.
An An
Assim, A∗ possui duas linhas iguais e pelo Corol´ rio 2.12 na p´ gina 103, det( A∗ ) =
a a
0. Mas, o determinante de A∗ desenvolvido segundo a sua i-´ sima linha e exata-
e ´
¸˜
mente a equacao (2.10).
¸˜ ´
A demonstracao de (2.11) e feita de forma an´ loga, mas usando o item (d) do Teo-
a
rema 2.13, ou seja, que det( A) = det( At ).
Teorema 2.18. Se A e uma matriz n × n, ent˜ o
´ a
A(adj( A)) = (adj( A)) A = det( A) In
Marco 2012
¸ Reginaldo J. Santos

130. 118 Invers˜ o de Matrizes e Determinantes
a
¸˜
Demonstracao. O produto da matriz A pela matriz adjunta de A e dada por
´

a11 a12 . . . a1n

 
. . ˜ ˜
a j1 ˜
. .   a11 ... ... an1
 
 . ... .
 ˜
  a12
... ˜
a j2 ... ˜
an2


 ai1 ai2 . . . ain  
 
.
. ... .
. ... .
.

 . . .
 
 .
. .
.

... ...

 . ... .  ˜
a1n ˜
a jp ˜
ann
an1 an2 . . . anp
O elemento de posicao i, j de A adj( A) e
¸˜ ´
n
( A adj( A))ij = ∑ aik a jk = ai1 a j1 + ai2 a j2 + . . . ain a jn .
˜ ˜ ˜ ˜
k =1
¸˜
Pelo Lema 2.17, equacao (2.10) e do Teorema 2.11 na p´ gina 102 segue-se que
a
det( A) se i = j
( A adj( A))ij =
0 se i = j.
Assim,
 
det( A) 0 ... 0
 0 det( A) ... 0 
A adj( A) =   = det( A) In .
 
.
. .
.
 . ... . 
0 0 ... det( A)
Analogamente, usando Lema 2.17, ¸˜
equacao (2.11), se prova que
adj( A) A = det( A) In .
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

131. 2.2 Determinantes 119
Exemplo 2.20. Vamos mostrar que se uma matriz A e singular, ent˜ o adj( A) tamb´ m
´ a e
´
e singular. Vamos separar em dois casos.
¯
(a) Se A = 0, ent˜ o adj( A) tamb´ m e a matriz nula, que e singular.
a e ´ ´
¯ a a ¯
(b) Se A = 0, ent˜ o pelo Teorema 2.18 na p´ gina 117, adj( A) A = 0. Mas, ent˜ o,
a
se adj( A) fosse invert´vel, ent˜ o A seria igual a matriz nula (por que?), que
ı a `
estamos assumindo n˜ o ser este o caso. Portanto, adj( A) tem que ser singular.
a
Corol´ rio 2.19. Seja A uma matriz n × n. Se det( A) = 0, ent˜ o
a a
1
A −1 = adj( A) ;
det( A)
1
¸˜
Demonstracao. Se det( A) = 0, ent˜ o definindo B =
a adj( A), pelo Teorema 2.18
det( A)
temos que
1 1 1
A B = A( adj( A)) = ( A adj( A)) = det( A) In = In .
det( A) det( A) det( A)
Aqui, usamos a propriedade (j) do Teorema 1.1 na p´ gina 8. Portanto, A e invert´vel
a ´ ı
e B e a inversa de A.
´
Exemplo 2.21. No Exemplo 2.17 na p´ gina 111 mostramos como obter rapidamente
a
a inversa de ma matriz 2 × 2. Usando o Corol´ rio 2.19 podemos tamb´ m obter a
a e
inversa de uma matriz 2 × 2,
a b
A= ,
c d
Marco 2012
¸ Reginaldo J. Santos

132. 120 Invers˜ o de Matrizes e Determinantes
a
1 1 d −b
A −1 = adj( A) = , se det( A) = 0
det( A) det( A) −c a
Ou seja, a inversa de uma matriz 2 × 2 e facilmente obtida trocando-se a posicao
´ ¸˜
dos elementos da diagonal principal, trocando-se o sinal dos outros elementos e
dividindo-se todos os elementos pelo determinante de A.
Exemplo 2.22. Vamos calcular a inversa da matriz
 
1 2 3
B= 0 3 2 .
0 0 −2
A sua adjunta foi calculada no Exemplo 2.19 na p´ gina 116. Assim,
a
1 −2 5 
  
−6 4 −5 3 6
1 1 
B −1 = adj( B) = 0 −2 −2  =  0 1
3
1  .
3
det( B) −6 0 0 3 0 0 −1
2
Corol´ rio 2.20 (Regra de Cramer). Se o sistema linear AX = B e tal que a matriz A e n × n e invert´vel, ent˜ o a
a ´ ´ ı a
solu¸ ao do sistema e dada por
c˜ ´
det( A1 ) det( A2 ) det( An )
x1 = , x2 = , . . . , xn = ,
det( A) det( A) det( A)
em que A j e a matriz que se obtem de A substituindo-se a sua j-´sima coluna por B, para j = 1, . . . , n.
´ e
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

133. 2.2 Determinantes 121
¸˜
Demonstracao. Como A e invert´vel, pelo Corol´ rio 2.19
´ ı a
1
X = A −1 B = adj( A) B.
det( A)
A entrada x j e dada por
´
1 det( A j )
xj = ˜ ˜
( a b + . . . + anj bn ) = ,
det( A) 1j 1 det( A)
em que A j e a matriz que se obtem de A substituindo-se a sua j-´ sima coluna por
´ e
B, para j = 1, . . . , n e det( A j ) foi calculado fazendo o desenvolvimento em cofatores
em relacao a j-´ sima coluna de A j .
¸˜ e
Se a matriz A n˜ o e invert´vel, ent˜ o a regra de Cramer n˜ o pode ser aplicada. Pode
a ´ ı a a
ocorrer que det( A) = det( A j ) = 0, para j = 1, . . . , n e o sistema n˜ o tenha solucao
a ¸˜
´ ´
(verifique!). A regra de Cramer tem um valor teorico, por fornecer uma formula para
¸˜ ´
a solucao de um sistema linear, quando a matriz do sistema e quadrada e invert´vel. ı
Marco 2012
¸ Reginaldo J. Santos

134. 122 Invers˜ o de Matrizes e Determinantes
a
Exerc´cios Num´ ricos (respostas na p´ gina 540)
ı e a
2.2.1. Se det( A) = −3, encontre
(a) det( A2 ); (b) det( A3 ); (c) det( A−1 ); (d) det( At );
2.2.2. Se A e B s˜ o matrizes n × n tais que det( A) = −2 e det( B) = 3, calcule det( At B−1 ).
a
2.2.3. Seja A = ( aij )3×3 tal que det( A) = 3. Calcule o determinante das matrizes a seguir:
   
a11 a12 a13 + a12 a11 + a12 a11 − a12 a13
(a)  a21 a22 a23 + a22  (b)  a21 + a22 a21 − a22 a23 
a31 a32 a33 + a32 a31 + a32 a31 − a32 a33
2.2.4. Calcule o determinante das matrizes a seguir:
ert tert cos βt sen βt
(a) (b)
rert (1 + rt)ert α cos βt − β sen βt α sen βt + β cos βt
¸˜
2.2.5. Calcule o determinante de cada uma das matrizes seguintes usando operacoes elementares para trans-
form´ -las em matrizes triangulares superiores.
a
   
1 −2 3 1 2 1 3 1
 5 −9 6 3   1 0 1 1 
(a) 
 −1
 (b)  .
2 −6 −2   0 2 1 0 
2 8 6 1 0 1 2 3
2.2.6. Determine todos os valores de λ para os quais det( A − λIn ) = 0, em que
   
0 1 2 1 0 0
(a) A =  0 0 3  (b) A =  −1 3 0 
0 0 0 3 2 −2
   
2 −2 3 2 2 3
(c) A =  0 3 −2  (d) A =  1 2 1 
0 −1 2 2 −2 1
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

135. 2.2 Determinantes 123
 
x1
2.2.7. Determine os valores de λ ∈ R tais que existe X =  .  = 0 que satisfaz
¯
 . 
. AX = λX.
xn
   
2 0 0 2 3 0
(a) A =  3 −1 0 ; (b) A =  0 1 0 ;
 0 4 3   0 0 2 
1 2 3 4 2 2 3 4
 0 −1 3 2   0 2 3 2 
(c) A = 
 ; (d) A =  .
0 0 3 3  0 0 1 1 
0 0 0 2 0 0 0 1
¸˜
2.2.8. Para as matrizes do exerc´cio anterior, e os valores de λ encontrados, encontre a solucao geral do sistema
ı
AX = λX, ou equivalentemente, do sistema homogˆ neo ( A − λIn ) X = 0.
e ¯
Marco 2012
¸ Reginaldo J. Santos

136. 124 Invers˜ o de Matrizes e Determinantes
a
Exerc´cios usando o M ATLAB
ı
Comandos do M ATLAB :
>> det(A) calcula o determinante da matriz A.
Comando do pacote GAAL:
¸˜
>> detopelp(A) calcula o determinante de A aplicando operacoes elementares at´ que a matriz esteja na
e
forma triangular superior.
e a ´
2.2.9. Vamos fazer um experimento no M ATLAB para tentar ter uma id´ ia do qu˜ o comum e encontrar ma-
trizes invert´veis. No prompt do M ATLAB digite a seguinte linha:
ı
>> c=0; for n=1:1000,A=randi(2);if(det(A)~=0),c=c+1;end,end,c
(n˜ o esqueca das v´rgulas e pontos e v´rgulas!). O que esta linha est´ mandando o M ATLAB
a ¸ ı ı a ´
fazer e o
seguinte:
• Criar um contador c e atribuir a ele o valor zero.
• Atribuir a vari´ vel A, 1000 matrizes 2 × 2 com entradas inteiras aleatorias entre −5 e 5.
` a ´
• Se det(A) = 0, ent˜ o o contador c e acrescido de 1.
a ´
• No final o valor existente na vari´ vel c e escrito.
a ´
Qual a conclus˜ o que vocˆ tira do valor obtido na vari´ vel c?
a e a
2.2.10. Resolva, com o M ATLAB , os Exerc´cios Num´ ricos a partir do Exerc´cio 4.
ı e ı
Exerc´cios Teoricos
ı ´
2.2.11. Mostre que se det( AB) = 0, ent˜ o ou A e singular ou B e singular.
a ´ ´
2.2.12. O determinante de AB e igual ao determinante de BA? Justifique.
´
2.2.13. Mostre que se A e uma matriz n˜ o singular tal que A2 = A, ent˜ o det( A) = 1.
´ a a
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

137. 2.2 Determinantes 125
¯
2.2.14. Mostre que se Ak = 0, para algum k inteiro positivo, ent˜ o A e singular.
a ´
2.2.15. Mostre que se At = A−1 , ent˜ o det( A) = ±1;
a
2.2.16. Mostre que se α e um escalar e A e uma matriz n × n, ent˜ o det(αA) = αn det( A).
´ ´ a
2.2.17. Mostre que A, n × n, e invert´vel se, e somente se, At A e invert´vel.
´ ı ´ ı
2.2.18. Sejam A e P matrizes n × n, sendo P invert´vel. Mostre que det( P−1 AP) = det( A).
ı
2.2.19. Mostre que se uma matriz A = ( aij )n×n e triangular superior, (isto e, os elementos situados abaixo da
´ ´
diagonal s˜ o iguais a zero) ent˜ o det( A) = a11 a22 . . . ann .
a a
a b
2.2.20. (a) Mostre que se A = , ent˜ o det( A) = 0 se, e somente se, uma linha e multiplo escalar da
a ´ ´
c d
outra. E se A for uma matriz n × n?
(b) Mostre que se uma linha Ai de uma matriz A = ( aij )n×n , e tal que Ai = αAk + βAl , para α e β
´
escalares e i = k, l, ent˜ o det( A) = 0.
a
(c) Mostre que se uma linha Ai de uma matriz A = ( aij )n×n , e tal que Ai = ∑ αk Ak , para α1 , . . . , αk
´
k =i
escalares, ent˜ o det( A) = 0.
a
´
2.2.21. Mostre que o determinante de Vandermonde e dado por
1 x 1 x 1 . . . x 1 −1
2 n
 
 1 x 2 x 2 . . . x n −1 
∏ ( x i − x j ).
2 2
Vn = det  . =
 
.
 . .
. .
.
. .  i> j
1 xn 2
xn ... x n −1
n
A express˜ o a direita significa o produto de todos os termos xi − x j tais que i > j e i, j = 1, . . . , n.
a `
(Sugest˜ o: Mostre primeiro que V3 = ( x3 − x2 )( x2 − x1 )( x3 − x1 ). Suponha que o resultado e verdadeiro
a ´
para matrizes de Vandermonde de ordem n − 1, mostre que o resultado e verdadeiro para matrizes de
´
Vandermonde de ordem n. Faca as seguintes operacoes nas colunas da matriz, − x1 Ci−1 + Ci → Ci , para
¸ ¸˜
i = n, . . . , 2. Obtenha Vn = ( xn − x1 ) . . . ( x2 − x1 )Vn−1 .)
Marco 2012
¸ Reginaldo J. Santos

138. 126 Invers˜ o de Matrizes e Determinantes
a
2.2.22. Sejam A, B e D matrizes p × p, p × (n − p) e (n − p) × (n − p), respectivamente. Mostre que
A B
det ¯ = det( A) det( D ).
0 D
(Sugest˜ o: O resultado e claramente verdadeiro para n = 2. Suponha que o resultado seja verdadeiro
a ´
para matrizes de ordem n − 1. Desenvolva o determinante da matriz em termos da 1a coluna, escreva
.
o resultado em termos de determinantes de ordem n − 1 e mostre que o resultado e verdadeiro para
´
matrizes de ordem n.)
2.2.23. Dˆ um exemplo de sistema linear de 3 equacoes e 3 incognitas, AX = B, em que det( A) = det( A1 ) =
e ¸˜ ´
det( A2 ) = det( A3 ) = 0 e o sistema n˜ o tenha solucao, em que A j e a matriz que se obtem de A
a ¸˜ ´
substituindo-se a sua j-´ sima coluna por B, para j = 1, . . . , n.
e
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

139. 2.2 Determinantes 127
e ¸˜
Apˆ ndice III: Demonstracao do Teorema 2.11 na p´ gina 102
a
¸˜ ´
Demonstracao do Teorema 2.10 na pagina 100 para k > 1. Deixamos como
exerc´cio para o leitor a verificacao de que para matrizes 2 × 2 o resultado e verda-
ı ¸˜ ´
deiro. Supondo que o resultado seja verdadeiro para matrizes (n − 1) × (n − 1),
vamos provar para matrizes n × n. Sejam
     
A1 A1 A1
.
.  .   . 
 .   . 
 

 . 
  .   . 
 A k −1   A k −1   A k −1 
     
A =  αX + βY  , B =  X  e C =  Y  .
     
 A k +1   A k +1   A k +1 
     
.
.
 .   . 
 .   . 
 
 .  . .
An An An
˜ ˜ ˜
Suponha que k = 2, . . . , n. As matrizes A1j , B1j e C1j so diferem na (k − 1)-´ sima
´ e
linha (lembre-se que a primeira linha e retirada!). Al´ m disso, a (k − 1)-´ sima linha
´ e e
˜ ´ ˜
de A1j e igual a α vezes a linha correspondente de B1j mais β vezes a linha cor-
˜
respondente de C1j (esta e a relacao que vale para a k-´ sima linha de A). Como
´ ¸˜ e
estamos supondo o resultado verdadeiro para matrizes (n − 1) × (n − 1), ent˜ o a
˜ ˜ ˜
det( A1j ) = α det( B1j ) + β det(C1j ). Assim,
n
det( A) = ∑ (−1)1+ j a1j det( A1j )
˜
j =1
n
= ∑ (−1)1+ j a1j ˜ ˜
α det( B1j ) + β det(C1j )
j =1
n n
= α ∑ (−1)1+ j b1j det( B1j ) + β ∑ (−1)1+ j c1j det(C1j )
˜ ˜
j =1 j =1
= α det( B) + β det(C ),
Marco 2012
¸ Reginaldo J. Santos

140. 128 Invers˜ o de Matrizes e Determinantes
a
pois a1j = b1j = c1j , para j = 1, . . . , n.
Lema 2.21. Sejam E1 = [ 1 0 . . . 0 ], E2 = [ 0 1 0 . . . 0 ], . . . , En = [ 0 . . . 0 1 ]. Se A e uma matriz n × n, cuja i-´sima
´ e
linha e igual a Ek , para algum k (1 ≤ k ≤ n), ent˜ o
´ a
det( A) = (−1)i+k det( Aik ).
˜
¸˜ ´ a
Demonstracao. E f´ cil ver que para matrizes 2 × 2 o lema e verdadeiro. Suponha que
´
ele seja verdadeiro para matrizes (n − 1) × (n − 1) e vamos provar que ele e verda-
´
deiro para matrizes n × n. Podemos supor que 1 < i ≤ n.
Seja Bj a matriz (n − 2) × (n − 2) obtida de A eliminando-se as linhas 1 e i e as
colunas j e k, para 1 ≤ j ≤ n.
˜ ´
Para j < k, a matriz A1j e uma matriz (n − 1) × (n − 1) cuja (i − 1)-´ sima linha e igual
e ´
˜ ´
a Ek−1 . Para j > k, a matriz A1j e uma matriz (n − 1) × (n − 1) cuja (i − 1)-´ sima
e
linha e igual a Ek . Como estamos supondo o lema verdadeiro para estas matrizes
´
e como pelo Teorema 2.10 na p´ gina 100 se uma matriz tem uma linha nula o seu
a
´ a ˜
determinante e igual a zero, ent˜ o det( A1k ) = 0, segue-se que
 (−1)(i−1)+(k−1) det( Bj ) se j < k,

˜
det( A1j ) = 0 se j = k, (2.12)
(−1)(i−1)+k det( Bj ) se j > k.

Usando (2.12), obtemos
n
det( A) = ∑ (−1)1+ j a1j det( Aij )
˜
j =1
n n
= ∑ (−1)1+ j a1j (−1)(i−1)+(k−1) det( Bj ) + ∑ (−1)1+ j a1j (−1)(i−1)+k det( Bj )
j<k j>k
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

141. 2.2 Determinantes 129
Por outro lado, temos que
n n
(−1)i+k det( Aik ) = (−1)i+k
˜ ∑ (−1)1+ j a1j det( Bj ) + ∑ (−1)1+( j−1) a1j det( Bj )
j<k j>k
´ ¸˜ ˜
E simples a verificacao de que as duas expressoes acima s˜ o iguais.
a
¸˜
Demonstracao do Teorema 2.11 na pagina 102.´
Pelo Teorema 2.14 na p´ gina 107 basta provarmos o resultado para o desenvolvi-
a
mento em termos das linhas de A. Sejam E1 = [1 0 . . . 0], E2 = [0 1 0 . . . 0], . . . , En =
[0 . . . 0 1]. Observe que a linha i de A pode ser escrita como Ai = ∑n=1 aij Ej . Seja Bj
j
a matriz obtida de A substituindo-se a linha i por Ej . Pelo Teorema 2.10 na p´ gina a
100 e o Lema 2.21 segue-se que
n n
det( A) = ∑ aij det( Bj ) = ∑ (−1)i+ j aij det( Aij ).
˜
j =1 j =1
Marco 2012
¸ Reginaldo J. Santos

142. 130 Invers˜ o de Matrizes e Determinantes
a
Teste do Cap´tulo
ı
1. Calcule o determinante da matriz seguinte usando ¸˜
operacoes elementares para transform´ -la em uma
a
matriz triangular superior.  
1 3 9 7
 2 3 2 5 
 
 0 3 4 1 
4 6 9 1
2. Se poss´vel, encontre a inversa da seguinte matriz:
ı
 
1 0 0 2
 0 1 0 0 
 
 0 0 1 0 
2 0 0 2
3. Encontre todos os valores de λ para os quais a matriz A − λI4 tem inversa, onde
 
2 0 0 0
 2 0 0 0 
A=  1 2

1 0 
3 2 −1 2
4. Responda Verdadeiro ou Falso, justificando:
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

143. 2.2 Determinantes 131
(a) Se A2 = −2A4 , ent˜ o ( I + A2 )−1 = I − 2A2 ;
a
(b) Se At = − A2 e A e n˜ o singular, ent˜ o determinante de A e -1;
´ a a ´
(c) Se B = AAt A−1 , ent˜ o det( A) = det( B).
a
(d) det( A + B) = det A + det B
Marco 2012
¸ Reginaldo J. Santos

144. 3
Vetores no Plano e no Espaco
¸
Muitas grandezas f´sicas, como velocidade, forca, deslocamento e impulso, para se-
ı ¸
¸˜
rem completamente identificadas, precisam, al´ m da magnitude, da direcao e do
e
sentido. Estas grandezas s˜ o chamadas grandezas vetoriais ou simplesmente veto-
a
res.
Geometricamente, vetores s˜ o representados por segmentos (de retas) orientados
a
(segmentos de retas com um sentido de percurso) no plano ou no espaco. A ponta
¸
´
da seta do segmento orientado e chamada ponto final ou extremidade e o outro
´
ponto extremo e chamado de ponto inicial ou origem do segmento orientado.
¸˜
Segmentos orientados com mesma direcao, mesmo sentido e mesmo comprimento
¸˜
representam o mesmo vetor. A direcao, o sentido e o comprimento do vetor s˜ o
a
¸˜
definidos como sendo a direcao, o sentido e o comprimento de qualquer um dos
segmentos orientados que o representam.
132

145. 133
Figura 3.1 – Segmentos orientados representando o mesmo vetor
Marco 2012
¸ Reginaldo J. Santos

146. 134 Vetores no Plano e no Espaco
¸
´ ´ ¸˜
Este fato e an´ logo ao que ocorre com os numeros racionais e as fracoes. Duas
a
¸˜ ´
fracoes representam o mesmo numero racional se o numerador e o denominador
¸˜ ¸˜
de cada uma delas estiverem na mesma proporcao. Por exemplo, as fracoes 1/2, 2/4
´ ¸˜
e 3/6 representam o mesmo numero racional. A definicao de igualdade de vetores
tamb´ m e an´ loga a igualdade de numeros racionais. Dois numeros racionais a/b e
e ´ a ´ ´
c/d s˜ o iguais, quando ad = bc. Dizemos que dois vetores s˜ o iguais se eles possuem
a a
¸˜
o mesmo comprimento, a mesma direcao e o mesmo sentido.
Na Figura 3.1 temos 4 segmentos orientados, com origens em pontos diferentes, que
representam o mesmo vetor, ou seja, s˜ o considerados como vetores iguais, pois
a
¸˜
possuem a mesma direcao, mesmo sentido e o mesmo comprimento.
Se o ponto inicial de um representante de um vetor V e A e o ponto ´
−→
final e B, ent˜ o escrevemos
´ a V = AB
−→
q
AB
B
¨
¨ B
¨¨
q
¨
¨
A
3.1 ¸˜
Soma de Vetores e Multiplicacao por Escalar
A soma, V + W, de dois vetores V e W e determinada da seguinte forma:
´
• tome um segmento orientado que representa V;
• tome um segmento orientado que representa W, com origem na extremidade
de V;
• o vetor V + W e representado pelo segmento orientado que vai da origem de V
´
at´ a extremidade de W.
e
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

147. 3.1 ¸˜
Soma de Vetores e Multiplicacao por Escalar 135
W
W
V U
W +U
W
+
V
W
V
+
+
V V
W
V +U
W)
(V + U)
(W +
W V+
Figura 3.2 – V + W = W + V Figura 3.3 – V + (W + U ) = (V + W ) + U
Marco 2012
¸ Reginaldo J. Santos

148. 136 Vetores no Plano e no Espaco
¸
´
Da Figura 3.2, deduzimos que a soma de vetores e comutativa, ou seja,
V + W = W + V, (3.1)
para quaisquer vetores V e W. Observamos tamb´ m que a soma V + W est´ na
e a
diagonal do paralelogramo determinado por V e W, quando est˜ o representados
a
com a mesma origem.
´
Da Figura 3.3, deduzimos que a soma de vetores e associativa, ou seja,
V + (W + U ) = (V + W ) + U, (3.2)
para quaisquer vetores V, W e U.
´
O vetor que tem a sua origem coincidindo com a sua extremidade e chamado vetor
¯
nulo e denotado por 0. Segue ent˜ o, que
a
¯ ¯
V + 0 = 0 + V = V, (3.3)
para todo vetor V.
Para qualquer vetor V, o sim´ trico de V, denotado por −V, e o vetor que tem mesmo
e ´
comprimento, mesma direcao e sentido contr´ rio ao de V. Segue ent˜ o, que
¸˜ a a
¯
V + (−V ) = 0. (3.4)
Definimos a diferen¸ a W menos V, por
c
W − V = W + (−V ).
¸˜
Segue desta definicao, de (3.1), (3.2), (3.4) e de (3.3) que
¯
W + (V − W ) = (V − W ) + W = V + (−W + W ) = V + 0 = V.
Assim, a diferenca V − W e um vetor que somado a W d´ V, portanto ele vai da
¸ ´ a
extremidade de W at´ a extremidade de V, desde que V e W estejam representados
e
por segmentos orientados com a mesma origem.
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

149. 3.1 ¸˜
Soma de Vetores e Multiplicacao por Escalar 137
V −W
V V V −W
−W W W
Figura 3.4 – A diferenca V − W
¸
Marco 2012
¸ Reginaldo J. Santos

150. 138 Vetores no Plano e no Espaco
¸
A multiplica¸ ao de um vetor V por um escalar α, α V, e determinada pelo vetor que
c˜ ´
possui as seguintes caracter´sticas:
ı
¯
(a) e o vetor nulo, se α = 0 ou V = 0,
´
(b) caso contr´ rio,
a
i. tem comprimento |α| vezes o comprimento de V,
ii. a direcao e a mesma de V (neste caso, dizemos que eles s˜ o paralelos),
¸˜ ´ a
iii. tem o mesmo sentido de V, se α > 0 e
tem o sentido contr´ rio ao de V, se α < 0.
a
¸˜
As propriedades da multiplicacao por escalar ser˜ o apresentadas mais a frente. Se
a
´ ´ ´ a
W = α V, dizemos que W e um multiplo escalar de V. E f´ cil ver que dois vetores
´ ´
n˜ o nulos s˜ o paralelos (ou colineares) se, e somente se, um e um multiplo escalar
a a
do outro.
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

151. 3.1 ¸˜
Soma de Vetores e Multiplicacao por Escalar 139
V
3V
−2V
1
2V
¸˜
Figura 3.5 – Multiplicacao de vetor por escalar
Marco 2012
¸ Reginaldo J. Santos

152. 140 Vetores no Plano e no Espaco
¸
¸˜
As operacoes com vetores podem ser definidas utilizando um sistema de coordena-
das retangulares ou cartesianas. Em primeiro lugar, vamos considerar os vetores no
plano.
Seja V um vetor no plano. Definimos as componentes de V como sendo as coorde-
nadas (v1 , v2 ) do ponto final do representante de V que tem ponto inicial na origem.
Vamos identificar o vetor com as suas componentes e vamos escrever simplesmente
V = ( v1 , v2 ).
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

153. 3.1 ¸˜
Soma de Vetores e Multiplicacao por Escalar 141
y y
V = ( v1 , v2 ) P = ( x, y)
v2 y
−→
OP
v1 O x
O x x
Figura 3.6 – As componentes do vetor V no Figura 3.7 – As coordenadas de P s˜ o iguais as
a
−→
plano componentes de OP
Marco 2012
¸ Reginaldo J. Santos

154. 142 Vetores no Plano e no Espaco
¸
−→
Assim, as coordenadas de um ponto P s˜ o iguais as componentes do vetor OP, que
a
vai da origem do sistema de coordenadas ao ponto P. Em particular, o vetor nulo,
¯
0 = (0, 0). Em termos das componentes, podemos realizar facilmente as operacoes:
¸˜
¸˜
soma de vetores e multiplicacao de vetor por escalar.
• Como ilustrado na Figura 3.8, a soma de dois vetores V = (v1 , v2 ) e W =
(w1 , w2 ) e dada por
´
V + W = ( v 1 + w1 , v 2 + w2 ) ;
• Como ilustrado na Figura 3.9, a multiplica¸ ao de um vetor V = (v1 , v2 ) por um
c˜
´
escalar α e dada por
α V = ( α v1 , α v2 ).
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

155. 3.1 ¸˜
Soma de Vetores e Multiplicacao por Escalar 143
y
y
V +W αv2
v2+w2 αV
V
v2
v2
V
w2
W
x
v1 αv1
v1 w1 v 1 + w1 x
¸˜
Figura 3.9 – A multiplicacao de vetor por escalar
Figura 3.8 – A soma de dois vetores no plano
no plano
Marco 2012
¸ Reginaldo J. Santos

156. 144 Vetores no Plano e no Espaco
¸
Definimos as componentes de um vetor no espa¸ o de forma an´ loga a que fizemos
c a
com vetores no plano. Vamos inicialmente introduzir um sistema de coordenadas
retangulares no espa¸ o. Para isto, escolhemos um ponto como origem O e como ei-
c
xos coordenados, trˆ s retas orientadas (com sentido de percurso definido), passando
e
pela origem, perpendiculares entre si, sendo uma delas vertical orientada para cima.
Estes ser˜ o os eixos x, y e z. O eixo z e o eixo vertical. Os eixos x e y s˜ o horizon-
a ´ a
tais e satisfazem a seguinte propriedade. Suponha que giramos o eixo x pelo menor
angulo at´ que coincida com o eixo y. Se os dedos da m˜ o direita apontam na direcao
ˆ e a ¸˜
do semieixo x positivo de forma que o semieixo y positivo esteja do lado da palma
da m˜ o, ent˜ o o polegar aponta no sentido do semieixo z positivo. Cada par de ei-
a a
xos determina um plano chamado de plano coordenado. Portanto os trˆ s planos e
coordenados s˜ o: xy, yz e xz.
a
A cada ponto P no espaco associamos um terno de numeros ( x, y, z), chamado de
¸ ´
coordenadas do ponto P como segue.
• Trace uma reta paralela ao eixo z, passando por P;
• A intersecao da reta paralela ao eixo z, passando por P, com o plano xy e o
¸˜ ´
ponto P . As coordenadas de P , ( x, y), no sistema de coordenadas xy s˜ o as
a
duas primeiras coordenadas de P.
• A terceira coordenada e igual ao comprimento do segmento PP , se P estiver
´
acima do plano xy e ao comprimento do segmento PP com o sinal negativo, se
P estiver abaixo do plano xy.
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

157. 3.1 ¸˜
Soma de Vetores e Multiplicacao por Escalar 145
z z
z
P = ( x, y, z) P = ( x, y, z)
z
x y x y
x P y x y
Figura 3.10 – As coordenadas de um ponto no espaco
¸
Marco 2012
¸ Reginaldo J. Santos

158. 146 Vetores no Plano e no Espaco
¸
As coordenadas de um ponto P s˜ o determinadas tamb´ m da maneira dada a seguir.
a e
• Passe trˆ s planos por P paralelos aos planos coordenados.
e
• A intersecao do plano paralelo ao plano xy, passando por P, com o eixo z de-
¸˜
termina a coordenada z.
• A intersecao do plano paralelo ao plano xz, passando por P, com o eixo y de-
¸˜
termina a coordenada y
• A intersecao do plano paralelo ao plano yz, passando por P, com o eixo x de-
¸˜
termina a coordenada x.
Agora, estamos prontos para utilizarmos um sistema de coordenadas cartesianas
tamb´ m nas operacoes de vetores no espaco. Seja V um vetor no espaco. Como no
e ¸˜ ¸ ¸
caso de vetores do plano, definimos as componentes de V como sendo as coordena-
das (v1 , v2 , v3 ) do ponto final do representante de V que tem ponto inicial na origem.
Tamb´ m vamos identificar o vetor com as suas componentes e vamos escrever sim-
e
plesmente
V = ( v1 , v2 , v3 ).
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

159. 3.1 ¸˜
Soma de Vetores e Multiplicacao por Escalar 147
z z
v3 z
V = ( v1 , v2 , v3 ) P = ( x, y, z)
−→
OP
v1 v2 x y
O
x y x y
Figura 3.11 – As componentes de um vetor no Figura 3.12 – As coordenadas de P s˜ o iguais as
a
−→
espaco
¸ componentes de OP
Marco 2012
¸ Reginaldo J. Santos

160. 148 Vetores no Plano e no Espaco
¸
−→
Assim, as coordenadas de um ponto P s˜ o iguais as componentes do vetor OP que
a
vai da origem do sistema de coordenadas ao ponto P. Em particular, o vetor nulo,
¯
0 = (0, 0, 0). Assim como fizemos para vetores no plano, para vetores no espaco ¸
¸˜
a soma de vetores e a multiplicacao de vetor por escalar podem ser realizadas em
termos das componentes.
• Se V = (v1 , v2 , v3 ) e W = (w1 , w2 , w3 ), ent˜ o a adicao de V com W e dada por
a ¸˜ ´
V + W = ( v 1 + w1 , v 2 + w2 , v 3 + w3 ) ;
• Se V = (v1 , v2 , v3 ) e α e um escalar, ent˜ o a multiplicacao de V por α e dada por
´ a ¸˜ ´
α V = ( α v1 , α v2 , α v3 ).
Exemplo 3.1. Se V = (1, −2, 3), W = (2, 4, −1), ent˜ o
a
V + W = (1 + 2, −2 + 4, 3 + (−1)) = (3, 2, 2), 3V = (3 · 1, 3 (−2), 3 · 3) = (3, −6, 9).
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

161. 3.1 ¸˜
Soma de Vetores e Multiplicacao por Escalar 149
z
V Q
P
O
x y
−→ −→ −→
Figura 3.13 – V = PQ=OQ − OP
Marco 2012
¸ Reginaldo J. Santos

162. 150 Vetores no Plano e no Espaco
¸
Quando um vetor V est´ representado por um segmento orientado com ponto ini-
a
cial fora da origem (Figura 3.13), digamos em P = ( x1 , y1 , z1 ), e ponto final em
Q = ( x2 , y2 , z2 ), ent˜ o as componentes do vetor V s˜ o dadas por
a a
−→ −→ −→
V = PQ=OQ − OP= ( x2 − x1 , y2 − y1 , z2 − z1 ).
Portanto, as componentes de V s˜ o obtidas subtraindo-se as coordenadas do ponto
a
Q (extremidade) das do ponto P (origem). O mesmo se aplica a vetores no plano.
Exemplo 3.2. As componentes do vetor V que tem um representante com ponto ini-
cial P = (5/2, 1, 2) e ponto final Q = (0, 5/2, 5/2) s˜ o dadas por
a
−→
V = PQ= (0 − 5/2, 5/2 − 1, 5/2 − 2) = (−5/2, 3/2, 1/2).
c˜ ´ a ¸˜
Observa¸ ao. O vetor e “livre”, ele n˜ o tem posicao fixa, ao contr´ rio do ponto e do segmento orientado. Por
a
exemplo, o vetor V = (−5/2, 3/2, 1/2), no exemplo acima, estava representado por um segmento orientado
com a origem no ponto P = (5/2, 1, 2). Mas, poderia ser representado por um segmento orientado cujo ponto
inicial poderia estar em qualquer outro ponto.
Um vetor no espaco V = (v1 , v2 , v3 ) pode tamb´ m ser escrito na notacao matricial
¸ e ¸˜
como uma matriz linha ou como uma matriz coluna:
 
v1
V =  v2  ou V = v1 v2 v3 .
v3
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

163. 3.1 ¸˜
Soma de Vetores e Multiplicacao por Escalar 151
¸˜ ¸˜
Estas notacoes podem ser justificadas pelo fato de que as operacoes matriciais
         
v1 w1 v 1 + w1 v1 αv1
V + W =  v2  +  w2  =  v2 + w2  , αV = α  v2  =  αv2 
v3 w3 v 3 + w3 v3 αv3
ou
V +W = v1 v2 v3 + w1 w2 w3 = v 1 + w1 v 2 + w2 v 3 + w3 ,
αV = α v1 v2 v3 = αv1 αv2 αv3
¸˜
produzem os mesmos resultados que as operacoes vetoriais
V + W = ( v 1 , v 2 , v 3 ) + ( w1 , w2 , w3 ) = ( v 1 + w1 , v 2 + w2 , v 3 + w3 ) ,
αV = α(v1 , v2 , v3 ) = (αv1 , αv2 , αv3 ).
O mesmo vale, naturalmente, para vetores no plano.
No teorema seguinte enunciamos as propriedades mais importantes da soma de ve-
¸˜
tores e multiplicacao de vetores por escalar.
Teorema 3.1. Sejam U, V e W vetores e α e β escalares. S˜ o v´ lidas as seguintes propriedades:
a a
(a) U + V = V + U; (e) α( βU ) = (αβ)U;
(b) (U + V ) + W = U + (V + W ); (f) α(U + V ) = αU + αV;
¯
(c) U + 0 = U; (g) (α + β)U = αU + βU;
¯
(d) U + (−U ) = 0; (h) 1U = U.
Marco 2012
¸ Reginaldo J. Santos

164. 152 Vetores no Plano e no Espaco
¸
¸˜ ´
Demonstracao. Segue diretamente das propriedades da algebra matricial (Teorema 1.1
na p´ gina 8).
a
Exemplo 3.3. Seja um triˆ ngulo ABC e sejam M e N os pontos m´ dios de AC e BC,
a e
respectivamente. Vamos provar que MN e paralelo a AB e tem comprimento igual
´
a metade do comprimento de AB.
Devemos provar que
−→ 1 −→
MN = AB .
2
C
M N
A B
Agora, a partir da figura acima temos que
−→ −→ −→
MN = MC + CN .
Como M e ponto m´ dio de AC e N e ponto m´ dio de BC, ent˜ o
´ e ´ e a
−→ 1 −→ −→ 1 −→
MC = AC e CN = CB .
2 2
Logo,
−→ 1 −→ 1 −→ 1 −→ −→ 1 −→
MN = AC + CB= ( AC + CB) = AB .
2 2 2 2
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

165. 3.1 ¸˜
Soma de Vetores e Multiplicacao por Escalar 153
−→ −→
Exemplo 3.4. Dados quatro pontos A, B, C e X tais que AX = λ AB, vamos escre-
−→ −→ −→
ver CX como combina¸ ao linear de CA e CB, isto e, como uma soma de multiplos
c˜ ´ ´
−→ −→
escalares de CA e CB.
−→ −→ −→ −→
Como AX = λ AB, ent˜ o os vetores AX e AB s˜ o paralelos e portanto o ponto X so
a a ´
pode estar na reta definida por A e B. Vamos desenh´ -lo entre A e B, mas isto n˜ o
a a
¸˜
representar´ nenhuma restricao, como veremos a seguir.
a
O vetor que vai de C para X, pode ser escrito como uma soma de um vetor que vai
de C para A com um vetor que vai de A para X,
−→ −→ −→
CX =CA + AX .
B
X
C
A
−→ −→ −→ −→ −→
Agora, por hipotese AX = λ AB, o que implica que CX =CA +λ AB.
´
−→ −→ −→ −→ −→ −→ −→
Mas, AB=CB − CA, portanto CX =CA +λ(CB − CA). Logo,
−→ −→ −→
CX = (1 − λ) CA +λ CB .
Observe que:
−→ −→
• Se λ = 0, ent˜ o CX =CA.
a
Marco 2012
¸ Reginaldo J. Santos

166. 154 Vetores no Plano e no Espaco
¸
−→ −→
• Se λ = 1, ent˜ o CX =CB.
a
−→ −→ −→
1
• Se λ = 1/2, ent˜ o CX =
a 2 CA + 1 CB.
2
−→ −→ −→
2
• Se λ = 1/3, ent˜ o CX =
a 3 CA + 1 CB.
3
• Se 0 ≤ λ ≤ 1, ent˜ o X pertence ao segmento AB, enquanto que se λ < 0 ou
a
λ > 1, ent˜ o X pertence a um dos prolongamentos do segmento AB.
a
Exemplo 3.5. Vamos mostrar, usando vetores, que o ponto m´ dio de um segmento
e
que une os pontos A = ( x1 , y1 , z1 ) e B = ( x2 , y2 , z2 ) e
´
x1 + x2 y1 + y2 z1 + z2
M= , , .
2 2 2
−→ −→
1
O ponto M e o ponto m´ dio de AB se, e somente se, AM =
´ e 2 AB. Ent˜ o, aplicando
a
−→ −→ −→
o exemplo anterior (com o ponto C sendo a origem O), OM = 1 OA + 1 OB. Como
2 2
as coordenadas de um ponto s˜ o iguais as componentes do vetor que vai da origem
a
−→
e 2
1
at´ aquele ponto, segue-se que OM = 1 ( x1 , y1 , z1 ) + 2 ( x2 , y2 , z2 ) e
x1 + x2 y1 + y2 z1 + z2
M= , , .
2 2 2
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

167. 3.1 ¸˜
Soma de Vetores e Multiplicacao por Escalar 155
Exerc´cios Num´ ricos (respostas na p´ gina 548)
ı e a
−→ −→
3.1.1. Determine o ponto C tal que AC = 2 AB sendo A = (0, −2) e B = (1, 0).
3.1.2. Uma reta no plano tem equacao y = 2x + 1. Determine um vetor paralelo a esta reta.
¸˜
3.1.3. Determine uma equacao para a reta no plano que e paralela ao vetor V = (2, 3) e passa pelo ponto
¸˜ ´
P0 = (1, 2).
3.1.4. Determine o vetor X, tal que 3X − 2V = 15( X − U ).
6X − 2Y = U
3.1.5. Determine os vetores X e Y tais que
3X + Y = U+V
3.1.6. Determine as coordenadas da extremidade do segmento orientado que representa o vetor V = (3, 0, −3),
sabendo-se que sua origem est´ no ponto P = (2, 3, −5).
a
3.1.7. Quais s˜ o as coordenadas do ponto P , sim´ trico do ponto P = (1, 0, 3) em relacao ao ponto M =
a e ¸˜
−→ −→
(1, 2, −1)? (Sugest˜ o: o ponto P e tal que o vetor MP = − MP)
a ´
´
3.1.8. Verifique se os pontos dados a seguir s˜ o colineares, isto e, pertencem a uma mesma reta:
a
(a) A = (5, 1, −3), B = (0, 3, 4) e C = (0, 3, −5);
(b) A = (−1, 1, 3), B = (4, 2, −3) e C = (14, 4, −15);
3.1.9. Dados os pontos A = (1, −2, −3), B = (−5, 2, −1) e C = (4, 0, −1). Determine o ponto D tal que A, B, C
e D sejam v´ rtices consecutivos de um paralelogramo.
e
3.1.10. Verifique se o vetor U e combinacao linear (soma de multiplos escalares) de V e W:
´ ¸˜ ´
(a) V = (9, −12, −6), W = (−1, 7, 1) e U = (−4, −6, 2);
(b) V = (5, 4, −3), W = (2, 1, 1) e U = (−3, −4, 1);
´
3.1.11. Verifique se e um paralelogramo o quadril´ tero de v´ rtices (n˜ o necessariamente consecutivos)
a e a
Marco 2012
¸ Reginaldo J. Santos

168. 156 Vetores no Plano e no Espaco
¸
(a) A = (4, −1, 1), B = (9, −4, 2), C = (4, 3, 4) e D = (4, −21, −14)
(b) A = (4, −1, 1), B = (9, −4, 2), C = (4, 3, 4) e D = (9, 0, 5)
3.1.12. Quais dos seguintes vetores s˜ o paralelos U = (6, −4, −2), V = (−9, 6, 3), W = (15, −10, 5).
a
Exerc´cios usando o M ATLAB
ı
>> V=[v1,v2,v3] cria um vetor V, usando as componentes num´ ricas v1, v2, v3. Por exemplo >>
e
V=[1,2,3] cria o vetor V = (1, 2, 3);
´ ´ ´
>> V+W e a soma de V e W; >> V-W e a diferenca V menos W; >> num*V e o produto do vetor V pelo escalar
¸
num;
>> subs(expr,x,num) substitui x por num na express˜ o expr;
a
¸˜ ¸˜
>> solve(expr) determina a solucao da equacao expr=0;
Comandos gr´ ficos do pacote GAAL:
a
>> desvet(P,V) desenha o vetor V com origem no ponto P e >> desvet(V) desenha o vetor V com origem
no ponto O = (0, 0, 0).
>> po([P1;P2;...;Pn]) desenha os pontos P1, P2, ..., Pn.
>> lineseg(P1,P2,’cor’) desenha o segmento de reta P1P2. >> tex(P,’texto’) coloca o texto no
ponto P.
>> axiss reescala os eixos com a mesma escala. >> eixos desenha os eixos coordenados.
>> box desenha uma caixa em volta da figura. >> rota faz uma rotacao em torno do eixo z. >>
¸˜
zoom3(fator) amplifica a regi˜ o pelo fator.
a
3.1.13. Coloque em duas vari´ veis V e W dois vetores do plano ou do espaco a seu crit´ rio
a ¸ e
¸˜
(a) Use a funcao ilsvw(V,W) para visualizar a soma dos dois vetores.
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

169. 3.1 ¸˜
Soma de Vetores e Multiplicacao por Escalar 157
´ ¸˜ ¸˜
(b) Coloque em uma vari´ vel a um numero e use a funcao ilav(a,V) para visualizar a multiplicacao
a
do vetor V pelo escalar a.
3.1.14. Use o M ATLAB para resolver os Exerc´cios Num´ ricos a partir do Exerc´cio 1.3.
ı e ı
Exerc´cios Teoricos
ı ´
e a e ´
3.1.15. Demonstre que o segmento que une os pontos m´ dios dos lados n˜ o paralelos de um trap´ zio e paralelo
−→ −→
as bases, e sua medida e a m´ dia aritm´ tica das medidas das bases. (Sugest˜ o: mostre que MN = 1 ( AB
` ´ e e a 2
−→ −→ −→
+ DC ) e depois conclua que MN e um multiplo escalar de AB. Revise o Exemplo 3.3 na p´ gina 152)
´ ´ a
D C
M N
A B
3.1.16. Demonstre que as diagonais de um paralelogramo se cortam ao meio. (Sugest˜ o: Sejam M e N os pontos
a
−→
e ¯ ent˜ o conclua que M = N.)
m´ dios das duas diagonais do paralelogramo. Mostre que o vetor MN = 0, a
Marco 2012
¸ Reginaldo J. Santos

170. 158 Vetores no Plano e no Espaco
¸
D C
M N
A B
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

171. 3.1 ¸˜
Soma de Vetores e Multiplicacao por Escalar 159
3.1.17. Considere o triˆ ngulo ABC e sejam M o ponto m´ dio de BC, N o ponto m´ dio de AC e P o ponto m´ dio
a e e e
de AB. Mostre que as medianas (os segmentos AM, BN e CP) se cortam num mesmo ponto que divide
−→ −→
2
as medianas na proporcao 2/3 e 1/3. (Sugest˜ o: Sejam G, H e I os pontos definidos por AG =
¸˜ a 3 AM,
−→ −→ −→ −→ −→ −→
2 2 ¯ ¯
BH = 3 BN e CI = 3 CP. Mostre que GH = 0, GI = 0, conclua que G = H = I.)
C
N
H G M
I
A
P B
3.1.18. Sejam A, B e C pontos quaisquer com A = B. Prove que:
−→ −→
(a) Um ponto X pertence a reta determinada por A e B ( AX = λ AB) se, e somente se,
−→ −→ −→
CX = α CA + β CB, com α + β = 1.
−→ −→
(b) Um ponto X pertence ao interior do segmento AB ( AX = λ AB, com 0 < λ < 1) se, e somente se,
−→ −→ −→
CX = α CA + β CB, com α > 0, β > 0 e α + β = 1.
−→ −→
(c) Um ponto X e um ponto interior ao triˆ ngulo ABC ( A X = λ A B , com 0 < λ < 1, em que A e um
´ a ´
ponto interior ao segmento AC e B e interior ao segmento CB) se, e somente se,
´
−→ −→ −→
CX = α CA + β CB, com α > 0, β > 0 e α + β < 1.
Marco 2012
¸ Reginaldo J. Santos

172. 160 Vetores no Plano e no Espaco
¸
B
C
A
¯ ¯
3.1.19. Mostre que se αV = 0, ent˜ o α = 0 ou V = 0.
a
3.1.20. Se αU = αV, ent˜ o U = V ? E se α = 0 ?
a
¯
3.1.21. Se αV = βV, ent˜ o α = β ? E se V = 0 ?
a
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

173. 3.2 Produtos de Vetores 161
3.2 Produtos de Vetores
3.2.1 Norma e Produto Escalar
J´ vimos que o comprimento de um vetor V e definido como sendo o comprimento
a ´
de qualquer um dos segmentos orientados que o representam. O comprimento do
vetor V tamb´ m e chamado de norma de V e e denotado(a) por ||V ||. Segue do
e ´ ´
Teorema de Pit´ goras que a norma de um vetor pode ser calculada usando as suas
a
componentes, por
||V || = v2 + v2 ,
1 2
no caso em que V = (v1 , v2 ) e um vetor no plano, e por
´
||V || = v2 + v2 + v2 ,
1 2 3
no caso em que V = (v1 , v2 , v3 ) e um vetor no espaco (verifique usando as Figuras
´ ¸
3.14 e 3.15).
Marco 2012
¸ Reginaldo J. Santos

174. 162 Vetores no Plano e no Espaco
¸
y z
V = ( v1 , v2 , v3 )
V = ( v1 , v2 )
||
| |V
| v2 | | v3 |
|v 1 |
| v1 | x |v2 |
x y
Figura 3.14 – A norma de um vetor V no plano Figura 3.15 – A norma de um vetor V no espaco
¸
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

175. 3.2 Produtos de Vetores 163
´
Um vetor de norma igual a 1 e chamado vetor unit´ rio.
a
A distˆ ncia entre dois pontos P = ( x1 , y1 , z1 ) e Q = ( x2 , y2 , z2 ) e igual a norma do
a ´ `
−→ −→ −→ −→
vetor PQ (Figura 3.13 na p´ gina 149). Como PQ=OQ − OP= ( x2 − x1 , y2 − y1 , z2 −
a
z1 ), ent˜ o a distˆ ncia de P a Q e dada por
a a ´
−→
dist( P, Q) = || PQ || = ( x2 − x1 )2 + ( y2 − y1 )2 + ( z2 − z1 )2 .
Analogamente, a distˆ ncia entre dois pontos P = ( x1 , y1 ) e Q = ( x2 , y2 ) no plano e
a ´
−→
igual a norma do vetor PQ, que e dada por
` ´
−→
dist( P, Q) = || PQ || = ( x2 − x1 )2 + ( y2 − y1 )2 .
Exemplo 3.6. A norma do vetor V = (1, −2, 3) e
´
√
||V || = 12 + (−2)2 + 32 = 14.
A distˆ ncia entre os pontos P = (2, −3, 1) e Q = (−1, 4, 5) e
a ´
−→ √
dist( P, Q) = || PQ || = ||(−1 − 2, 4 − (−3), 5 − 1)|| = ||(−3, 7, 4)|| = (−3)2 + 72 + 42 = 74.
Se V = (v1 , v2 , v3 ) e α e um escalar, ent˜ o da definicao da multiplicacao de vetor por
´ a ¸˜ ¸˜
escalar e da norma de um vetor segue-se que
||αV || = ||(αv1 , αv2 , αv3 )|| = (αv1 )2 + (αv2 )2 + (αv3 )2 = α2 ( v2 + v2 + v2 ),
1 2 3
Marco 2012
¸ Reginaldo J. Santos

176. 164 Vetores no Plano e no Espaco
¸
ou seja,
||αV || = |α| ||V ||. (3.5)
Dado um vetor V n˜ o nulo, o vetor
a
1
U= V.
||V ||
e um vetor unit´ rio na dire¸ ao de V, pois por (3.5), temos que
´ a c˜
1
||U || = ||V || = 1.
||V ||
Exemplo 3.7. Um vetor unit´ rio na direcao do vetor V = (1, −2, 3) e o vetor
a ¸˜ ´
1 1 1 −2 3
U= V= √ (1, −2, 3) = ( √ , √ , √ ).
||V || 14 14 14 14
O angulo entre dois vetores n˜ o nulos, V e W, e definido pelo angulo θ determinado
ˆ a ´ ˆ
por V e W que satisfaz 0 ≤ θ ≤ π, quando eles est˜ o representados com a mesma
a
origem (Figura 3.16).
Quando o angulo θ entre dois vetores V e W e reto (θ = 90o), ou um deles e o vetor
ˆ ´ ´
nulo, dizemos que os vetores V e W s˜ o ortogonais ou perpendiculares entre si.
a
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

177. 3.2 Produtos de Vetores 165
V
V
θ
θ W W
ˆ
Figura 3.16 – Angulo entre dois vetores, agudo (` esquerda) e obtuso (` direita)
a a
Marco 2012
¸ Reginaldo J. Santos

178. 166 Vetores no Plano e no Espaco
¸
´
Vamos definir, agora, um produto entre dois vetores, cujo resultado e um escalar.
´ ¸˜
Por isso ele e chamado produto escalar. Este produto tem aplicacao, por exemplo,
ı ¸ ´
em F´sica: o trabalho realizado por uma forca e o produto escalar do vetor forca pelo
¸
´
vetor deslocamento, quando a forca aplicada e constante.
¸
¸˜
Definicao 3.1. O produto escalar ou interno de dois vetores V e W e definido por
´
0, se V ou W e o vetor nulo,
´
V ·W =
||V || ||W || cos θ, caso contr´ rio,
a
´ ˆ
em que θ e o angulo entre eles.
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

179. 3.2 Produtos de Vetores 167
Quando os vetores s˜ o dados em termos das suas componentes n˜ o sabemos direta-
a a
ˆ
mente o angulo entre eles. Por isso, precisamos de uma forma de calcular o produto
ˆ
escalar que n˜ o necessite do angulo entre os vetores.
a
Marco 2012
¸ Reginaldo J. Santos

180. 168 Vetores no Plano e no Espaco
¸
V
V V −W
V −W
θ
θ W W
a `
Figura 3.17 – Triˆ ngulo formado por representantes de V, W e V − W. A esquerda o angulo entre V e W e agudo
ˆ ´
` ´
e a direita e obtuso.
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

181. 3.2 Produtos de Vetores 169
Se V e W s˜ o dois vetores n˜ o nulos e θ e o angulo entre eles, ent˜ o pela lei dos
a a ´ ˆ a
cossenos,
||V − W ||2 = ||V ||2 + ||W ||2 − 2||V || ||W || cos θ.
Assim,
1
V · W = ||V || ||W || cos θ = ||V ||2 + ||W ||2 − ||V − W ||2 . (3.6)
2
a a ´
J´ temos ent˜ o uma formula para calcular o produto escalar que n˜ o depende dire-
a
ˆ
tamente do angulo entre eles. Substituindo-se as coordenadas dos vetores em (3.6)
obtemos uma express˜ o mais simples para o c´ lculo do produto interno.
a a
Por exemplo, se V = (v1 , v2 , v3 ) e W = (w1 , w2 , w3 ) s˜ o vetores no espaco, ent˜ o
a ¸ a
substituindo-se ||V ||2 = v2 + v2 + v2 , ||W ||2 = w1 + w2 + w3 e ||V − W ||2 = (v1 −
1 2 3
2 2 2
w1 )2 + (v2 − w2 )2 + (v3 − w3 )2 em (3.6) os termos v2 e wi s˜ o cancelados e obtemos
i
2 a
V · W = v 1 w1 + v 2 w2 + v 3 w3 .
Teorema 3.2. O produto escalar ou interno, V · W, entre dois vetores e dado por
´
V · W = v 1 w1 + v 2 w2 ,
se V = (v1 , v2 ) e W = (w1 , w2 ) s˜ o vetores no plano e por
a
V · W = v 1 w1 + v 2 w2 + v 3 w3 ,
se V = (v1 , v2 , v3 ) e W = (w1 , w2 , w3 ) s˜ o vetores no espa¸ o.
a c
Marco 2012
¸ Reginaldo J. Santos

182. 170 Vetores no Plano e no Espaco
¸
Exemplo 3.8. Sejam V = (0, 1, 0) e W = (2, 2, 3). O produto escalar de V por W e
´
dado por
V · W = v 1 w1 + v 2 w2 + v 3 w3 = 0 · 2 + 1 · 2 + 0 · 3 = 2 .
ˆ
Podemos usar o Teorema 3.2 para determinar o angulo entre dois vetores n˜ o nulos,
a
V e W. O cosseno do angulo entre V e W e, ent˜ o, dado por
ˆ ´ a
V ·W
cos θ = .
||V || ||W ||
Se V e W s˜ o vetores n˜ o nulos e θ e o angulo entre eles, ent˜ o
a a ´ ˆ a
(a) θ e agudo (0 ≤ θ < 90o ) se, e somente se, V · W > 0,
´
(b) θ e reto (θ = 90o ) se, e somente se, V · W = 0 e
´
(c) θ e obtuso (90o < θ ≤ 180o ) se, e somente se, V · W < 0.
´
Exemplo 3.9. Vamos determinar o angulo entre uma diagonal de um cubo e uma de
ˆ
suas arestas. Sejam V1 = (1, 0, 0), V2 = (0, 1, 0) e V3 = (0, 0, 1) (Figura 3.18). Uma
diagonal do cubo e representada pelo vetor D dado por
´
D = V1 + V2 + V3 = (1, 1, 1) .
Ent˜ o o angulo entre D e V1 satisfaz
a ˆ
D · V1 1.1 + 0.1 + 0.1 1
cos θ = = √ √ = √
|| D ||||V1 || ( 12 + 12 + 12 )( 12 + 02 + 02 ) 3
ou seja,
1
θ = arccos( √ ) ≈ 54o .
3
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

183. 3.2 Produtos de Vetores 171
z
(0, 0, 1)
(1, 1, 1)
(1, 0, 0) θ
x (0, 1, 0)
y
ˆ
Figura 3.18 – Angulo entre a diagonal de um cubo e uma de suas arestas
Marco 2012
¸ Reginaldo J. Santos

184. 172 Vetores no Plano e no Espaco
¸
Teorema 3.3. Sejam U, V e W vetores e α um escalar. S˜ o v´ lidas as seguintes propriedades:
a a
(a) (comutatividade) U · V = V · U ;
(b) (distributividade) U · (V + W ) = U · V + U · W;
(c) (associatividade) α(U · V ) = (αU ) · V = U · (αV );
¯
(d) V · V = ||V ||2 ≥ 0, para todo V e V · V = 0 se, e somente se, V = 0.
¸˜
Demonstracao. Sejam U = (u1 , u2 , u3 ), V = (v1 , v2 , v3 ) e W = (w1 , w2 , w3 ).
(a) U · V = u1 v1 + u2 v2 + u3 v3 = v1 u1 + v2 u2 + v3 u3 = V · U;
(b) U · (V + W ) = (u1 , u2 , u3 ) · (v1 + w1 , v2 + w2 , v3 + w3 ) = u1 (v1 + w1 ) + u2 (v2 +
w2 ) + u 3 ( v 3 + w3 ) = ( u 1 v 1 + u 1 w1 ) + ( u 2 v 2 + u 2 w2 ) + ( u 3 v 3 + u 3 w3 ) = ( u 1 v 1 +
u2 v2 + u3 v3 ) + (u1 w1 + u2 w2 + u3 w3 ) = U · V + U · W;
(c) α(U · V ) = α(u1 v1 + u2 v2 + u3 v3 ) = (αu1 )v1 + (αu2 )v2 + (αu3 )v3 = (αU ) · V;
(d) V · V = ||V ||2 e uma soma de quadrados, por isso e sempre maior ou igual a
´ ´
´
zero e e zero se, e somente se, todas as parcelas s˜ o iguais a zero.
a
¸˜
3.2.2 Projecao Ortogonal
Dados dois vetores V e W a proje¸ ao ortogonal de V sobre W denotada por
c˜
projW V
e o vetor que e paralelo a W tal que V − projW V seja ortogonal a W (Figura 3.19).
´ ´
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

185. 3.2 Produtos de Vetores 173
V
V − projW V
V − projW V
V
projW V W projW V W
Figura 3.19 – Projecao ortogonal do vetor V sobre o vetor W
¸˜
Marco 2012
¸ Reginaldo J. Santos

186. 174 Vetores no Plano e no Espaco
¸
¸˜
Proposicao 3.4. Seja W um vetor n˜ o nulo. Ent˜ o, a proje¸ ao ortogonal de um vetor V em W e dada por
a a c˜ ´
V ·W
projW V = W.
||W ||2
Demonstracao. Sejam V1 = projW V e V2 = V − projW V. Como V1 e paralelo a W,
¸˜ ´
ent˜ o
a
V1 = αW. (3.7)
Assim,
V2 = V − αW .
Multiplicando-se escalarmente V2 por W e usando o Teorema 3.3 (d) obtemos
V2 · W = (V − αW ) · W = V · W − α||W ||2 . (3.8)
Mas, V2 e ortogonal a W, ent˜ o V2 · W = 0. Portanto, de (3.8) obtemos
´ a
V ·W
α= .
||W ||2
¸˜
Substituindo este valor de α na equacao (3.7) segue-se o resultado.
Exemplo 3.10. Sejam V = (2, −1, 3) e W = (4, −1, 2). Vamos encontrar dois vetores
V1 e V2 tais que V = V1 + V2 , V1 e paralelo a W e V2 e perpendicular a W (Figura 3.19).
´ ´
Temos que
V · W = 2 · 4 + (−1)(−1) + 3 · 2 = 15
||W ||2 = 42 + (−1)2 + 22 = 21 .
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

187. 3.2 Produtos de Vetores 175
V · W) 15 20 5 10
V1 = projW V = W= (4, −1, 2) = ( ,− , )
||W ||2 21 7 7 7
20 5 10 6 2 11
V2 = V − V1 = (2, −1, 3) − ( , − , ) = (− , − , ) .
7 7 7 7 7 7
3.2.3 Produto Vetorial
´
Vamos, agora, definir um produto entre dois vetores, cujo resultado e um vetor. Por
´ ¸˜
isso, ele e chamado produto vetorial. Este produto tem aplicacao, por exemplo, em
F´sica: a forca exercida sobre uma part´cula com carga unit´ ria mergulhada num
ı ¸ ı a
e ´
campo magn´ tico uniforme e o produto vetorial do vetor velocidade da part´cula
ı
pelo vetor campo magn´ tico.
e
Marco 2012
¸ Reginaldo J. Santos

188. 176 Vetores no Plano e no Espaco
¸
W
h = ||W || sen θ
||
| |W
θ
V
||V ||
´
Figura 3.20 – Area de um paralelogramo determinado por dois vetores
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

189. 3.2 Produtos de Vetores 177
¸˜
Definicao 3.2. Sejam V e W dois vetores no espaco. Definimos o produto vetorial, V × W, como sendo o vetor
¸
com as seguintes caracter´sticas:
ı
(a) Tem comprimento dado numericamente por
||V × W || = ||V || ||W || sen θ,
ou seja, a norma de V × W e numericamente igual a area do paralelogramo determinado por V e W.
´ ` ´
(b) Tem direcao perpendicular a V e a W.
¸˜
(c) Tem o sentido dado pela regra da m˜ o direita (Figura 3.21): Se o angulo entre V e W e θ, giramos o
a ˆ ´
vetor V de um angulo θ at´ que coincida com W e acompanhamos este movimento com os dedos da m˜ o
ˆ e a
direita, ent˜ o o polegar vai apontar no sentido de V × W.
a
Marco 2012
¸ Reginaldo J. Santos

190. 178 Vetores no Plano e no Espaco
¸
VxW
V
θ
W
V
θ
W
WxV
Figura 3.21 – Regra da m˜ o direita
a
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

191. 3.2 Produtos de Vetores 179
´
Da forma como definimos o produto vetorial e dif´cil o seu c´ lculo, mas as proprie-
ı a
´
dades que apresentaremos a seguir possibilitar˜ o obter uma formula para o produto
a
vetorial em termos das componentes dos vetores.
Teorema 3.5. Sejam U, V e W vetores no espa¸ o e α um escalar. S˜ o v´ lidas as seguintes propriedades:
c a a
(a) V × W = −(W × V ) (anti-comutatividade).
¯
(b) V × W = 0 se, e somente se, V = αW ou W = αV.
(c) (V × W ) · V = (V × W ) · W = 0.
(d) α(V × W ) = (αV ) × W = V × (αW ).
(e) V × (W + U ) = V × W + V × U e (V + W ) × U = V × U + W × U (Distributividade em rela¸ ao a soma de
c˜
vetores).
Demonstracao. (a) Pela definicao do produto vetorial V × W e W × V tˆ m o mesmo
¸˜ ¸˜ e
comprimento e a mesma direcao. Al´ m disso trocando-se V por W troca-se o
¸˜ e
sentido de V × W (Figura 3.21).
(b) ||V × W || = 0 se, e somente se, um deles e o vetor nulo ou sen θ = 0, em que θ
´
´ ˆ a ¯
e o angulo entre V e W, ou seja, V e W s˜ o paralelos. Assim, V × W = 0 se, e
somente se, V = αW ou W = αV.
¸˜
(c) Segue-se imediatamente da definicao do produto vetorial.
¸˜
(d) Segue-se facilmente da definicao do produto vetorial, por isso deixamos como
exerc´cio para o leitor.
ı
(e) Este item ser´ demonstrado no Apˆ ndice IV na p´ gina 201.
a e a
Marco 2012
¸ Reginaldo J. Santos

192. 180 Vetores no Plano e no Espaco
¸
Os vetores canonicos
ˆ
i = (1, 0, 0), j = (0, 1, 0) e k = (0, 0, 1)
s˜ o vetores unit´ rios (de norma igual a um) paralelos aos eixos coordenados. Todo
a a
vetor
V = ( v1 , v2 , v3 )
pode ser escrito como uma soma de multiplos escalares de i, j e k (combinacao linear),
´ ¸˜
pois
V = ( v1 , v2 , v3 ) = (v1 , 0, 0) + (0, v2 , 0) + (0, 0, v3 ) =
= v1 (1, 0, 0) + v2 (0, 1, 0) + v3 (0, 0, 1) =
= v1 i + v2 j + v3 k. (3.9)
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

193. 3.2 Produtos de Vetores 181
z z
v3 k
k
V = ( v1 , v2 , v3 )
i j
v1 i v2 j
x y x y
Figura 3.22 – Vetores i, j e k Figura 3.23 – V = v1 i + v2 j + v3 k
Marco 2012
¸ Reginaldo J. Santos

194. 182 Vetores no Plano e no Espaco
¸
¸˜ ¸˜
Da definicao de produto vetorial podemos obter facilmente as seguintes relacoes:
¯
i × i = 0, ¯
j × j = 0, ¯
k × k = 0,
i × j = k, j × k = i, k × i = j,
j × i = −k, k × j = −i, i × k = − j.
´
Agora, estamos prontos para obter uma formula que dˆ o produto vetorial de dois
e
vetores em termos das suas componentes.
Teorema 3.6. Sejam V = (v1 , v2 , v3 ) e W = (w1 , w2 , w3 ) vetores no espa¸ o. Ent˜ o o produto vetorial V × W e dado
c a ´
por
v2 v3 v1 v3 v1 v2
V ×W = det , − det , det . (3.10)
w2 w3 w1 w3 w1 w2
¸˜
Demonstracao. De (3.9) segue-se que podemos escrever
V = v1 i + v2 j + v3 k e W = w1 i + w2 j + w3 k.
¸˜
Assim, pela distributividade do produto vetorial em relacao a soma, temos que
V ×W = ( v 1 i + v 2 j + v 3 k ) × ( w1 i + w2 j + w3 k )
= v 1 w1 ( i × i ) + v 1 w2 ( i × j ) + v 1 w3 ( i × k ) +
+ v 2 w1 ( j × i ) + v 2 w2 ( j × j ) + v 2 w3 ( j × k ) +
+ v 3 w1 ( k × i ) + v 3 w2 ( k × j ) + v 3 w3 ( k × k )
= ( v 2 w3 − v 3 w2 ) i + ( v 3 w1 − v 1 w3 ) j + ( v 1 w2 − v 2 w1 ) k
v2 v3 v1 v3 v1 v2
= det i − det j + det k
w2 w3 w1 w3 w1 w2
v2 v3 v1 v3 v1 v2
= det , − det , det .
w2 w3 w1 w3 w1 w2
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

195. 3.2 Produtos de Vetores 183
Marco 2012
¸ Reginaldo J. Santos

196. 184 Vetores no Plano e no Espaco
¸
Para obter as componentes do produto vetorial V × W procedemos como segue:
• Escreva a matriz:
V v1 v2 v3
= ;
W w1 w2 w3
• Para calcular a primeira componente de V × W, elimine a primeira coluna da
matriz acima e calcule o determinante da sub-matriz resultante. A segunda
´
componente e obtida, eliminando-se a segunda coluna e calculando-se o deter-
minante da sub-matriz resultante com o sinal trocado. A terceira e obtida como
´
a primeira, mas eliminando-se a terceira coluna.
Exemplo 3.11. Sejam V = i + 2 j − 2k e W = 3i + k. Vamos determinar o produto
vetorial V × W. Como
V 1 2 −2
= ,
W 3 0 1
ent˜ o
a
2 −2 1 −2 1 2
V ×W = det , − det , det = (2, −7, −6) .
0 1 3 1 3 0
Usando os vetores i, j e k o produto vetorial V × W, pode ser escrito em termos do
“determinante”
 
i j k
v2 v3 v1 v3 v1 v2
V × W = det  v1 v2 v3  = det i − det j + det k.
w2 w3 w1 w3 w1 w2
w1 w2 w3
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

197. 3.2 Produtos de Vetores 185
Q
R
P
´
Figura 3.24 – Area do triˆ ngulo PQR
a
Marco 2012
¸ Reginaldo J. Santos

198. 186 Vetores no Plano e no Espaco
¸
Exemplo 3.12. Vamos calcular a area do triˆ ngulo PQR em que (Figura 3.24)
´ a
P = (3, 2, 0), Q = (0, 4, 3) e R = (1, 0, 2).
Sejam
−→
V = RP= (3 − 1, 2 − 0, 0 − 2) = (2, 2, −2)
−→
W = RQ= (0 − 1, 4 − 0, 3 − 2) = (−1, 4, 1) .
Ent˜ o,
a
V × W = (10, 0, 10) = 10(1, 0, 1).
A area do triˆ ngulo PQR e a metade da area do paralelogramo com lados determi-
´ a ´ ´
nados por V e W. Assim,
1 √
´
Area = ||V × W || = 5 2.
2
3.2.4 Produto Misto
O produto (V × W ) · U e chamado produto misto de U, V e W. O resultado abaixo
´
mostra como calcular o produto misto usando as componentes dos vetores.
Teorema 3.7. Sejam U = u1 i + u2 j + u3 k, V = v1 i + v2 j + v3 k e W = w1 i + w2 j + w3 k. Ent˜ o,
a
 
v1 v2 v3
(V × W ) · U = det  w1 w2 w3  .
u1 u2 u3
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

199. 3.2 Produtos de Vetores 187
¸˜
Demonstracao. Segue do Teorema 3.2 na p´ gina 169, do Teorema 3.6 na p´ gina 182 e
a a
¸˜
da definicao de determinante de uma matriz que
v2 v3 v1 v3 v1 v2
(V × W ) · U = (u1 , u2 , u3 ) · det , − det , det
w2 w3 w1 w3 w1 w2
v2 v3 v1 v3 v1 v2
= u1 det − u2 det + u3 det
w2 w3 w1 w3 w1 w2
 
v1 v2 v3
= det  w1 w2 w3  .
u1 u2 u3
Exemplo 3.13. O produto misto dos vetores U = 2i − j + 3k, V = −i + 4 j + k e
W = 5i + j − 2 k e
´
   
v1 v2 v3 −1 4 1
(V × W ) · U = det  w1 w2 w3  = det  5 1 −2  = −84.
u1 u2 u3 2 −1 3
Marco 2012
¸ Reginaldo J. Santos

200. 188 Vetores no Plano e no Espaco
¸
V ×W
U
h = ||U || | cos θ |
W
θ
V
Figura 3.25 – Volume do paralelep´pedo determinado por V, W e U
ı
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

201. 3.2 Produtos de Vetores 189
Teorema 3.8. Dados trˆs vetores no espa¸ o, U, V e W,
e c
|(V × W ) · U |
e numericamente igual ao volume do paralelep´pedo determinado por U, V e W.
´ ı
¸˜
Demonstracao. O volume do paralelep´pedo determinado por U, V e W e igual ao pro-
ı ´
´ ¸˜
duto da area da base pela altura, ou seja, pela definicao do produto vetorial, o vo-
´
lume e dado por
Volume = ||V × W || h .
Mas, como vemos na Figura 3.25 a altura e h = ||U ||| cos θ |, o que implica que
´
Volume = ||V × W || ||U ||| cos θ | = |(V × W ) · U | .
Exemplo 3.14. Sejam V = 4i, W = 2i + 5 j e U = 3i + 3 j + 4k. O volume do para-
lelep´pedo com um v´ rtice na origem e arestas determinadas por U, V e W e dado
ı e ´
por  
4 0 0
volume = |(V × W ) · U | = | det  2 5 0  | = |80| = 80 .
3 3 4
Marco 2012
¸ Reginaldo J. Santos

202. 190 Vetores no Plano e no Espaco
¸
U
V W
Figura 3.26 – Paralelep´pedo determinado por U, V e W do Exemplo 3.14
ı
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

203. 3.2 Produtos de Vetores 191
Segue imediatamente do Teorema 3.7 e do Teorema 3.8 um crit´ rio para saber se trˆ s
e e
vetores s˜ o paralelos a um mesmo plano.
a
Corol´ rio 3.9. Sejam U = u1 i + u2 j + u3 k, V = v1 i + v2 j + v3 k e W = w1 i + w2 j + w3 k. Estes vetores s˜ o copla-
a a
nares (isto e, s˜ o paralelos a um mesmo plano) se, e somente se,
´ a
 
v1 v2 v3
(V × W ) · U = det  w1 w2 w3  = 0 .
u1 u2 u3
Exemplo 3.15. Vamos verificar que os pontos P = (0, 1, 1), Q = (1, 0, 2),
R = (1, −2, 0) e S = (−2, 2, −2) s˜ o coplanares, isto e, pertencem a um mesmo
a ´
plano. Com estes pontos podemos construir os vetores
−→
PQ= (1 − 0, 0 − 1, 2 − 1) = (1, −1, 1),
−→
PR= (1 − 0, −2 − 1, 0 − 1) = (1, −3, −1) e
−→
PS = (−2 − 0, 2 − 1, −2 − 1) = (−2, 1, −3)
−→
Os pontos P, Q, R e S pertencem a um mesmo plano se, e somente se, os vetores PQ,
−→ −→
PR e PS s˜ o coplanares. E isto acontece se, e somente se, o produto misto deles e
a ´
igual zero.  
−→ −→ −→ 1 −3 −1
( PR × PS ) · PQ= det  −2 1 −3  = 0.
1 −1 1
Assim, P, Q, R e S s˜ o coplanares.
a
Marco 2012
¸ Reginaldo J. Santos

204. 192 Vetores no Plano e no Espaco
¸
´ ¸˜
O resultado a seguir ser´ usado no proximo cap´tulo para deduzir as equacoes pa-
a ı
ram´ tricas do plano.
e
Corol´ rio 3.10. Sejam U, V e W vetores coplanares n˜ o nulos no espa¸ o.
a a c
(a) Ent˜ o a equa¸ ao vetorial
a c˜
¯
xU + yV + zW = 0
tem solu¸ ao n˜ o trivial, em que x, y e z s˜ o escalares.
c˜ a a
(b) Ent˜ o um dos vetores U, V ou W e combina¸ ao linear (soma de multiplos escalares) dos outros dois.
a ´ c˜ ´
(c) Se V e W s˜ o n˜ o paralelos, ent˜ o U e combina¸ ao linear de V e W.
a a a ´ c˜
¸˜
Demonstracao. (a) Seja A a matriz cujas colunas s˜ o U, V e W escritos como vetores
a
¯ ´
colunas. A equacao xU + yV + zW = 0 e equivalente ao sistema AX = 0. Se
¸˜ ¯
U, V e W s˜ o coplanares, ent˜ o
a a
det( A) = det( At ) = (U × V ) · W = 0.
¸˜ ¯
Logo a equacao xU + yV + zW = 0 tem solucao n˜ o trivial.
¸˜ a
¸˜ ¯
(b) Pelo item anterior a equacao xU + yV + zW = 0 possui solucao n˜ o trivial. Mas,
¸˜ a
se isto acontece, ent˜ o um dos escalares x ou y ou z pode ser diferente de zero.
a
Se x = 0, ent˜ o U = (−y/x )V + (−z/x )W, ou seja, o vetor U e combinacao
a ´ ¸˜
linear de V e W. De forma semelhante, se y = 0, ent˜ o V e combinacao linear
a ´ ¸˜
de U e W e se z = 0, ent˜ o W e combinacao linear de U e V.
a ´ ¸˜
(c) Como U, V e W s˜ o coplanares, ent˜ o a equacao xU + yV + zW = 0 possui
a a ¸˜ ¯
solucao n˜ o trivial com x = 0. Pois, caso contr´ rio yV + zW = 0
¸˜ a a ¯ com y ou z
n˜ o simultaneamente nulos o que implicaria que V e W seriam paralelos (por
a
que?). Logo U = (−y/x )V + (−z/x )W.
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

205. 3.2 Produtos de Vetores 193
Exemplo 3.16. Considere os vetores
−→
U = PQ= (1, −1, 1),
−→
V = PR= (1, −3, −1) e
−→
W = PS = (−2, 1, −3)
¸˜
do Exemplo 3.15 na p´ gina 191. A equacao
a
¯
xU + yV + zW = 0
´
e equivalente ao sistema

 x + y − 2z = 0
− x − 3y + z = 0
x − y − 3z = 0

Escalonando a matriz do sistema obtemos
     
1 1 −2 1 1 −2 1 1 −2
 −1 −3 1  ∼  0 −2 −1  ∼  0 −2 −1 
1 −1 −3 0 −2 −1 0 0 0
´
A ultima matriz corresponde ao sistema
x + y − 2z = 0
− 2y − z = 0
Assim
5α α ¯
U − V + αW = 0.
2 2
Logo
5 1
W = − U + V.
2 2
Verifique que realmente vale esta relacao entre os vetores U, V e W.
¸˜
Marco 2012
¸ Reginaldo J. Santos

206. 194 Vetores no Plano e no Espaco
¸
Exerc´cios Num´ ricos (respostas na p´ gina 550)
ı e a
3.2.1. Determine a equacao da reta no plano que e perpendicular ao vetor N = (2, 3) e passa pelo ponto
¸˜ ´
P0 = (−1, 1).
−→
3.2.2. Seja O = (0, 0, 0). Qual o lugar geom´ trico dos pontos P = ( x, y, z) tais que || OP ||2 = 4? Qual figura e
e ´
representada pela equacao x2 + y2 = 4?
¸˜
3.2.3. Sejam V = i + 2 j − 3k e W = 2i + j − 2k. Determine vetores unit´ rios paralelos aos vetores
a
(a) V + W; (b) V − W; (c) 2V − 3W.
3.2.4. Determine o valor de x para o qual os vetores V = xi + 3 j + 4k e W = 3i + j + 2k s˜ o perpendiculares.
a
3.2.5. Demonstre que n˜ o existe x tal que os vetores V = xi + 2 j + 4k e W = xi − 2 j + 3k s˜ o perpendiculares.
a a
ˆ
3.2.6. Ache o angulo entre os seguintes pares de vetores:
(a) 2i + j e j − k; (b) i + j + k e −2 j − 2k; (c) 3i + 3 j e 2i + j − 2k.
3.2.7. Decomponha W = −i − 3 j + 2k como a soma de dois vetores W1 e W2 , com W1 paralelo ao vetor j + 3k e
W2 ortogonal a este ultimo. (Sugest˜ o: revise o Exemplo 3.10 na p´ gina 174)
´ a a
3.2.8. Ache o vetor unit´ rio da bissetriz do angulo entre os vetores V = 2i + 2 j + k e W = 6i + 2 j − 3k. (Su-
a ˆ
a a ¸˜
gest˜ o: observe que a soma de dois vetores est´ na direcao da bissetriz se, e somente se, os dois tiverem o
mesmo comprimento. Portanto, tome multiplos escalares de V e W de forma que eles tenham o mesmo
´
¸˜
comprimento e tome o vetor unit´ rio na direcao da soma deles.)
a
3.2.9. Verifique se os seguintes pontos pertencem a um mesmo plano:
(a) A = (2, 2, 1), B = (3, 1, 2), C = (2, 3, 0) e D = (2, 3, 2);
(b) A = (2, 0, 2), B = (3, 2, 0), C = (0, 2, 1) e D = (10, −2, 1);
3.2.10. Calcule o volume do paralelep´pedo que tem um dos v´ rtices no ponto A = (2, 1, 6) e os trˆ s v´ rtices
ı e e e
adjacentes nos pontos B = (4, 1, 3), C = (1, 3, 2) e D = (1, 2, 1).
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

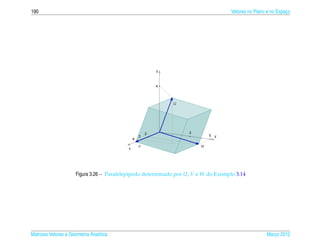
207. 3.2 Produtos de Vetores 195
3.2.11. Calcule a area do paralelogramo em que trˆ s v´ rtices consecutivos s˜ o A = (1, 0, 1), B = (2, 1, 3) e
´ e e a
C = (3, 2, 4).
3.2.12. Calcule a area do triˆ ngulo com v´ rtices A = (1, 2, 1), B = (3, 0, 4) e C = (5, 1, 3).
´ a e
√
3.2.13. Ache X tal que X × (i + k ) = 2(i + j − k) e || X || = 6.
√
3.2.14. Sabe-se que o vetor X e ortogonal a i + j e a −i + k, tem norma 3 e sendo θ o angulo entre X e j, tem-se
´ ˆ
cos θ > 0. Ache X.
3.2.15. Mostre que A = (3, 0, 2), B = (4, 3, 0) e C = (8, 1, −1) s˜ o v´ rtices de um triˆ ngulo retˆ ngulo. Em qual
a e a a
a ˆ
dos v´ rtices est´ o angulo reto?
e
3.2.16. Considere dois vetores V e W tais que ||V || = 5, ||W || = 2 e o angulo entre V e W e 60◦ . Determine,
ˆ ´
como combinacao linear de V e W (xV + yW):
¸˜
(a) Um vetor X tal que X · V = 20 e X · W = 5
¯
(b) Um vetor X tal que X × V = 0 e X · W = 12.
Exerc´cios usando o M ATLAB
ı
>> V=[v1,v2,v3] cria um vetor V, usando as componentes num´ ricas v1, v2, v3. Por exemplo >>
e
V=[1,2,3] cria o vetor V = (1, 2, 3);
>> subs(expr,x,num) substitui x por num na express˜ o expr;
a
¸˜ ¸˜
>> solve(expr) determina a solucao da equacao expr=0;
Comandos num´ ricos do pacote GAAL:
e
´
>> V=randi(1,3) cria um vetor aleatorio com componentes inteiras;
>> no(V) calcula a norma do vetor V.
Marco 2012
¸ Reginaldo J. Santos

208. 196 Vetores no Plano e no Espaco
¸
>> pe(V,W) calcula o produto escalar do vetor V pelo vetor W.
>> pv(V,W) calcula o produto vetorial do vetor V pelo vetor W.
Comandos gr´ ficos do pacote GAAL:
a
>> desvet(P,V) desenha o vetor V com origem no ponto P e >> desvet(V) desenha o vetor V com origem
no ponto O = (0, 0, 0).
>> po([P1;P2;...;Pn]) desenha os pontos P1, P2, ..., Pn.
>> lineseg(P1,P2,’cor’) desenha o segmento de reta P1P2.
>> eixos desenha os eixos coordenados.
>> box desenha uma caixa em volta da figura.
>> axiss reescala os eixos com a mesma escala.
>> rota faz uma rotacao em torno do eixo z.
¸˜
>> zoom3(fator) amplifica a regi˜ o pelo fator.
a
>> tex(P,’texto’) coloca o texto no ponto P.
3.2.17. Digite no prompt
demog21,
¸˜ ¸˜
(sem a v´rgula!). Esta funcao demonstra as funcoes gr´ ficas para vetores.
ı a
3.2.18. Coloque em duas vari´ veis V e W dois vetores bi-dimensionais ou tri-dimensionais a seu crit´ rio.
a e
¸˜ ´
(a) Use a funcao ilvijk(V) para visualizar o vetor V como uma soma de multiplos escalares
(combinacao linear) dos vetores i, j e k.
¸˜
(b) Use a funcao ilpv(V,W) para visualizar o produto vetorial V × W.
¸˜
(c) Use a funcao ilproj(W,V) para visualizar a projecao de V em W.
¸˜ ¸˜
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

209. 3.2 Produtos de Vetores 197
3.2.19. Use o M ATLAB para resolver os Exerc´cios Num´ ricos
ı e
Exerc´cios Teoricos
ı ´
´ ` ´ `
3.2.20. Mostre que em um triˆ ngulo isosceles a mediana relativa a base e perpendicular a base.
a
ˆ ´
3.2.21. Mostre que o angulo inscrito em uma semicircunferˆ ncia e reto.
e
−→ −→
Sugest˜ o para os proximos 2 exerc´cios: Considere o paralelogramo ABCD. Seja U = AB e V = AD.
a ´ ı
Observe que as diagonais do paralelogramo s˜ o U + V e U − V.
a
a a ´
3.2.22. Mostre que se as diagonais de um paralelogramo s˜ o perpendiculares ent˜ o ele e um losango.
e a ´
3.2.23. Mostre que se as diagonais de um paralelogramo tˆ m o mesmo comprimento ent˜ o ele e um retˆ ngulo.
a
¯
3.2.24. Se V · W = V · U e V = 0, ent˜ o W = U?
a
3.2.25. Mostre que se V e ortogonal a W1 e W2 , ent˜ o V e ortogonal a α1 W1 + α2 W2 .
´ a ´
3.2.26. Demonstre que as diagonais de um losango s˜ o perpendiculares. (Sugest˜ o: mostre que
a a
−→ −→ −→ −→ −→ −→
AC · BD = 0, usando o fato de que AB= DC e || AB || = || BC ||.)
3.2.27. Sejam V um vetor n˜ o nulo no espaco e α, β e γ os angulos que V forma com os vetores i, j e k, respecti-
a ¸ ˆ
vamente. Demonstre que
cos2 α + cos2 β + cos2 γ = 1 .
V ·i V·j V ·k
(Sugest˜ o: cos α =
a , cos β = e cos γ = )
||V ||||i || ||V |||| j|| ||V ||||k||
3.2.28. Demonstre que, se V e W s˜ o vetores quaisquer, ent˜ o:
a a
1
(a) V · W = ||V + W ||2 − ||V − W ||2 ;
4
Marco 2012
¸ Reginaldo J. Santos

210. 198 Vetores no Plano e no Espaco
¸
1
(b) ||V ||2 + ||W ||2 = ||V + W ||2 + ||V − W ||2 .
2
(Sugest˜ o:
a desenvolva os segundos membros das igualdades acima observando que
||V + W ||2 = (V + W ) · (V + W ) e ||V − W ||2 = (V − W ) · (V − W ))
3.2.29. Demonstre que se V e W s˜ o vetores quaisquer, ent˜ o:
a a
(a) |V · W | ≤ ||V || ||W ||;
(b) ||V + W || ≤ ||V || + ||W ||;
(Sugest˜ o: mostre que ||V + W ||2 = (V + W ) · (V + W ) ≤ (||V || + ||W ||)2 , usando o item anterior)
a
(c) ||V || − ||W || ≤ ||V − W ||.
(Sugest˜ o: defina U = V − W e aplique o item anterior a U e W)
a
3.2.30. O produto vetorial e associativo? Justifique a sua resposta. (Sugest˜ o: experimente com os vetores i, j, k)
´ a
¯
3.2.31. Se V × W = V × U e V = 0, ent˜ o W = U?
a
3.2.32. Demonstre que se V e W s˜ o vetores quaisquer no espaco, ent˜ o
a ¸ a
||V × W || ≤ ||V || ||W ||.
3.2.33. Se U, V e W s˜ o vetores no espaco, prove que |U · (V × W )| ≤ ||U || ||V || ||W ||. (Sugest˜ o: use o Teorema
a ¸ a
3.2 na p´ gina 169 e o exerc´cio anterior)
a ı
3.2.34. Mostre que U · (V × W ) = V · (W × U ) = W · (U × V ). (Sugest˜ o: use as propriedades do determinante)
a
3.2.35. Mostre que
(a) (αU1 + βU2 ) · (V × W ) = αU1 · (V × W ) + βU2 · (V × W );
(b) U · [(αV1 + βV2 ) × W ] = αU · (V1 × W ) + βU · (V2 × W );
(c) U · [V × (αW1 + βW2 )] = αU · (V × W1 ) + βU · (V × W2).
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

211. 3.2 Produtos de Vetores 199
(d) U · (V × W ) = U · [(V + αU + βW ) × W ].
(Sugest˜ o: use as propriedades dos produtos escalar e vetorial)
a
3.2.36. Prove a identidade de Lagrange
||V × W ||2 = ||V ||2 ||W ||2 − (V · W )2 .
3.2.37. Mostre que a area do triˆ ngulo com v´ rtices ( xi , yi ), para i = 1, 2, 3 e igual a | det( A)|/2, em que
´ a e ´
 
x1 y1 1
A =  x2 y2 1  .
x3 y3 1
(Sugest˜ o: Marque os pontos P1 = ( x1 , y1 , 1), P2 = ( x2 , y2 , 1), P3 = ( x3 , y3 , 1) e P1 = ( x1 , y1 , 0). O volume
a
−→ −→ −→
do paralelep´pedo determinado por P1 , P2 , P3 e P1 e dado por | P1 P1 · P1 P2 × P1 P3 |. Mas, a altura
ı ´
´ ´ ` ´ ´
deste paralelep´pedo e igual a 1. Assim, o seu volume e igual a area da base que e o paralelogramo
ı
−→ −→ −→
determinado por P1 , P2 e P3 . Observe que OP1 , P1 P2 e P1 P3 s˜ o paralelos ao plano xy.)
a
3.2.38. Sejam U1 , U2 e U3 trˆ s vetores unit´ rios mutuamente ortogonais. Se A = [ U1 U2 U3 ] e uma matriz
e a ´
3 × 3 cujas colunas s˜ o os vetores U1 , U2 e U3 , ent˜ o A e invert´vel e A−1 = At . (Sugest˜ o: mostre que
a a ´ ı a
At A = I3 .)
3.2.39. Sejam U = (u1 , u2 , u3 ), V = (v1 , v2 , v3 ) e W = (w1 , w2 , w3 ). Prove a formula seguinte para o produto
´
vetorial duplo
U × (V × W ) = (U · W )V − (U · V )W,
seguindo os seguintes passos:
(a) Prove que
U × (i × j ) = (U · j ) i − (U · i ) j
U × ( j × k) = (U · k ) j − (U · j ) k
U × (k × i ) = (U · i ) k − (U · k ) i
Marco 2012
¸ Reginaldo J. Santos

212. 200 Vetores no Plano e no Espaco
¸
(b) Prove usando o item anterior e as propriedades do produto vetorial que
U × (V × i ) = (U · i ) V − (U · V ) i
U × (V × j ) = (U · j ) V − (U · V ) j
U × (V × k ) = (U · k ) V − (U · V ) k
(c) Prove agora o caso geral usando o item anterior e as propriedades do produto vetorial.
3.2.40. (a) Prove que
[ A × ( B × C )] + [ B × (C × A)] + [C × ( A × B)] = 0
(Sugest˜ o: use o exerc´cio anterior).
a ı
¯
(b) Mostre que se ( A × C ) × B = 0, ent˜ oa
A × ( B × C ) = ( A × B) × C,
´
ou seja, o produto vetorial e, neste caso, associativo.
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

213. 3.2 Produtos de Vetores 201
e ¸˜
Apˆ ndice IV: Demonstracao do item (e) do Teorema 3.5 na p´ gina 179
a
¸˜ ¸˜
Vamos dividir a demonstracao da distributividade do produto vetorial em relacao a soma
V × (W + U ) = V × W + V × U e (V + W ) × U = V × U + W × U
da seguinte forma:
(a) (V × W ) · U > 0 se, e somente se, V, W e U satisfazem a regra da m˜ o direita, isto e, se o angulo entre
a ´ ˆ
V e W e θ, giramos o vetor V de um angulo θ at´ que coincida com W e acompanhamos este movimento
´ ˆ e
com os dedos da m˜ o direita, ent˜ o o polegar vai apontar no sentido de U.
a a
(b) (V × W ) · U = V · (W × U ), ou seja, pode-se trocar os sinais × e · em (V × W ) · U.
(c) V × (W + U ) = V × W + V × U e (V + W ) × U = V × U + W × U.
Provemos, agora, os trˆ s ´tens acima.
e ı
(a) Como vemos na Figura 3.25 na p´ gina 188 V, W e U satisfazem a regra da m˜ o direita se, e somente
a a
se, 0 < θ < π/2, ou seja, cos θ > 0, em que θ e o angulo entre V × W e U. Como, (V × W ) · U =
´ ˆ
||V × W ||||U || cos θ, ent˜ o V, W e U satisfazem a regra da m˜ o direita se, e somente se, (V × W ) · U > 0.
a a
´
(b) Como o produto escalar e comutativo, pelo Teorema 3.8 na p´ gina 189,
a
|(V × W ) · U | = |V · (W × U )|.
Agora, pelo item (a), temos que
(V × W ) · U e V · (W × U )
tˆ m o mesmo sinal, pois V, W e U satisfazem a regra da m˜ o direita se, e somente se, W, U e V tamb´ m
e a e
satisfazem.
¸˜
(c) Vamos provar a primeira igualdade e deixamos como exerc´cio para o leitor a demonstracao da segunda.
ı
Vamos mostrar que o vetor Y = V × (W + U ) − V × W − V × U e o vetor nulo. Para isso, vamos mostrar
´
que para qualquer vetor X no espaco X · Y = 0.
¸
Marco 2012
¸ Reginaldo J. Santos

214. 202 Vetores no Plano e no Espaco
¸
Pela distributividade do produto escalar, Teorema 3.3 item (b) na p´ gina 172, temos que
a
X · Y = X · V × (W + U ) − X · ( V × W ) − X · ( V × U ) .
Pelo item (b), temos que
X·Y = ( X × V ) · (W + U ) − ( X × V ) · W − ( X × V ) · U
= ( X × V ) · (W + U ) − ( X × V ) · (W + U ) = 0
Assim, X · Y = 0, para todo vetor X, em particular para X = Y, temos que Y · Y = ||Y ||2 = 0. Portanto
¯
Y = 0, ou seja, V × (W + U ) = V × W + V × U.
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

215. 3.2 Produtos de Vetores 203
Teste do Cap´tulo
ı
1. Mostre que os pontos A = (4, 0, 1), B = (5, 1, 3), C = (3, 2, 5), D = (2, 1, 3) s˜ o v´ rtices de um paralelo-
a e
´
gramo. Calcule a sua area.
2. Dado o triˆ ngulo de v´ rtices A = (0, 1, −1), B = (−2, 0, 1) e C = (1, −2, 0), determine a medida da altura
a e
relativa ao lado BC.
¯
3. Sejam U e V vetores no espaco, com V = 0.
¸
(a) Determine o numero α, tal que U − αV seja ortogonal a V.
´
(b) Mostre que (U + V ) × (U − V ) = 2V × U.
4. Determine x para que A = ( x, 1, 2), B = (2, −2, −3), C = (5, −1, 1) e D = (3, −2, −2) sejam coplanares.
Marco 2012
¸ Reginaldo J. Santos

216. 4
Retas e Planos
4.1 ¸˜
Equacoes de Retas e Planos
¸˜
4.1.1 Equacoes do Plano
¸˜
Equacao Geral
No plano a equacao geral de uma reta e ax + by + c = 0. No espaco um plano e o
¸˜ ´ ¸ ´
conjunto dos pontos P = ( x, y, z) que satisfazem a equacao
¸˜
ax + by + cz + d = 0, para a, b, c, d ∈ R,
´
que e chamada equa¸ ao geral do plano. Existe uma analogia entre uma reta no
c˜
¸˜ ´
plano e um plano no espaco. No plano, a equacao de uma reta e determinada se
¸
¸˜ ¸˜
forem dados sua inclinacao e um de seus pontos. No espaco, a inclinacao de um
¸
204

217. 4.1 ¸˜
Equacoes de Retas e Planos 205
´
plano e caracterizada por um vetor perpendicular a ele, chamado vetor normal ao
¸˜ ´
plano e a equacao de um plano e determinada se s˜ o dados um vetor normal e um
a
de seus pontos.
Marco 2012
¸ Reginaldo J. Santos

218. 206 Retas e Planos
N = ( a, b, c)
P0 = ( x0 , y0 , z0 )
π P = ( x, y, z)
Figura 4.1 – Plano perpendicular a N = ( a, b, c) e que passa por P0 = ( x0 , y0 , z0 )
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

219. 4.1 ¸˜
Equacoes de Retas e Planos 207
¸˜
Proposicao 4.1. A equa¸ ao geral de um plano π que passa por um ponto P0 = ( x0 , y0 , z0 ) e tem vetor normal N =
c˜
( a, b, c) e
´
ax + by + cz + d = 0 , (4.1)
em que d = −( ax0 + by0 + cz0 ).
¸˜
Demonstracao. Um ponto P = ( x, y, z) pertence ao plano π se, e somente se, o vetor
−→
P0 P for perpendicular ao vetor N, ou seja,
−→
N · P0 P= 0 . (4.2)
−→
Como, P0 P= ( x − x0 , y − y0 , z − z0 ), a equacao (4.2) pode ser reescrita como
¸˜
a( x − x0 ) + b(y − y0 ) + c(z − z0 ) = 0,
ou seja,
ax + by + cz − ( ax0 + by0 + cz0 ) = 0 .
Marco 2012
¸ Reginaldo J. Santos

220. 208 Retas e Planos
z
z z
−d
c
−d
a −d
b
x y
y x y
x
Figura 4.2 – Planos ax + d = 0, by + d = 0 e cz + d = 0
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

221. 4.1 ¸˜
Equacoes de Retas e Planos 209
z z z
−d
c
−d
c
−d
b
−d
a −d
a −d
b
x y y y
x x
Figura 4.3 – Planos by + cz + d = 0, ax + cz + d = 0 e ax + by + d = 0
Marco 2012
¸ Reginaldo J. Santos

222. 210 Retas e Planos
z z z
y
ax = 0
+ ,
0
cz
+ 0,
=
=
by =
cz
0
x
y
ax = 0 0, = 0
+ ,
cz x = + cz
= by
0
z = by =
0
ax +
y=
a x 0,
0,
y y y
+b
z=
x x x
0
Figura 4.4 – Planos ax + by + cz = 0
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

223. 4.1 ¸˜
Equacoes de Retas e Planos 211
z
z
−d
c
y
x
by = 0
+c ,
z=
0
−d −d
b
a
=0
x y
,
y
z=0
x
ax +b
Figura 4.5 – Planos ax + by + cz = 0 e ax + by + cz + d = 0
Marco 2012
¸ Reginaldo J. Santos

224. 212 Retas e Planos
Exemplo 4.1. Vamos encontrar a equacao do plano π que passa pelo ponto
¸˜
P0 = (1, −2, −2) e e perpendicular ao vetor N = (2, −1, 2). Da Proposicao 4.1,
´ ¸˜
¸˜ ´
a equacao do plano e da forma
ax + by + cz + d = 0 ,
em que os coeficientes de x, y e z s˜ o as componentes do vetor normal, ou seja, a = 2,
a
b = −1 e c = 2. Assim, a equacao de π e da forma
¸˜ ´
2x − y + 2z + d = 0 .
Para determinar o coeficiente d, ao inv´ s de usarmos a Proposicao 4.1, vamos usar o
e ¸˜
fato de que P0 = (1, −2, −2) pertence a π. Mas, o ponto P0 pertence a π se, e somente
¸˜
se, as suas coordenadas satisfazem a equacao de π, ou seja,
2 · 1 − 1 · (−2) + 2 · (−2) + d = 0 .
Logo, d = 2 + 2 − 4 = 0. Substituindo-se d = 0 na equacao anterior do plano
¸˜
¸˜ ´
obtemos que a equacao do plano π e
2x − y + 2z = 0 .
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

225. 4.1 ¸˜
Equacoes de Retas e Planos 213
z
2
2
4
y
x
Figura 4.6 – Plano 2x − y + 2z = 0
Marco 2012
¸ Reginaldo J. Santos

226. 214 Retas e Planos
¸˜ ´
No plano, a equacao de uma reta e determinada se forem dados dois pontos da reta.
¸ ¸˜ ´
Analogamente, no espaco, a equacao de um plano e determinada se s˜ o dados trˆ s
a e
pontos P1 , P2 e P3 n˜ o colineares (isto e, n˜ o pertencentes a uma mesma reta). Com
a ´ a
−→ −→
os trˆ s pontos podemos “formar” os vetores P1 P2 e P1 P3 (Figura 4.7).
e
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

227. 4.1 ¸˜
Equacoes de Retas e Planos 215
−→ −→
N = P1 P2 × P1 P3
P3 = ( x3 , y3 , z3 )
P1 = ( x1 , y1 , z1 )
π
P = ( x, y, z)
P2 = ( x2 , y2 , z2 )
Figura 4.7 – Plano que passa por trˆ s pontos
e
Marco 2012
¸ Reginaldo J. Santos

228. 216 Retas e Planos
z
1/4
1/2
1/2
y
x
Figura 4.8 – Plano 2x + 2y + 4z − 1 = 0
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

229. 4.1 ¸˜
Equacoes de Retas e Planos 217
Exemplo 4.2. Vamos encontrar a equacao do plano π que passa pelos pontos
¸˜
P1 = ( 2 , 0, 0), P2 = (0, 1 , 0) e P3 = (0, − 2 , 1 ). Com os trˆ s pontos podemos “for-
1
2
1
2 e
−→ −→
mar” os vetores P1 P2 e P1 P3 . O vetor
−→ −→ 1 1 1 1 1 1 1 1
N = P1 P2 × P1 P3 = (− , , 0) × (− , − , ) = ( , , )
2 2 2 2 2 4 4 2
´ ¸˜ ´
e um vetor normal ao plano. Assim, a equacao do plano e da forma
1 1 1
x + y + z + d = 0,
4 4 2
em que os coeficientes de x, y e z s˜ o as componentes do vetor N. Para determinar
a
1
o coeficiente d, vamos usar o fato de que o ponto P1 = ( 2 , 0, 0) pertence ao plano
π. Mas, o ponto P1 pertence a π se, e somente se, as suas coordenadas satisfazem a
¸˜
equacao de π, ou seja,
1 1 1 1
· + ·0+ ·0+ d = 0.
4 2 4 2
Logo, d = 1 . Finalmente, uma equacao do plano π e
8 ¸˜ ´
1 1 1 1
x+ y+ z− = 0
4 4 2 8
ou multiplicando por 8, obtemos
2x + 2y + 4z − 1 = 0.
¸˜
Alternativamente, podemos encontrar a equacao do plano da seguinte forma. Como
−→ −→ −→
vimos anteriormente (Corol´ rio 3.9 na p´ gina 191), trˆ s vetores, P1 P P1 P2 e P1 P3 , s˜ o
a a e a
´
coplanares se, e somente se, o produto misto entre eles e zero. Assim, um ponto
P = ( x, y, z) pertence a π se, e somente se,
−→ −→ −→
P1 P · ( P1 P2 × P1 P3 ) = 0 .
Marco 2012
¸ Reginaldo J. Santos

230. 218 Retas e Planos
Mas,
−→ 1
P1 P = ( x − , y, z)
2
−→ 1 1
P1 P2 = (− , , 0)
2 2
−→ 1 1 1
P1 P3 = (− , − , ).
2 2 2
Ent˜ o,
a
x− 1
 
2 y z
1 1 1 1 1 1
det  − 2 2 0  = (x − ) + y + z
1 1 1 4 2 4 2
−2 −2 2
¸˜ ´
e assim a equacao do plano e dada por
1 1 1 1
x + y + z − = 0.
4 4 2 8
ou multiplicando por 8,
2x + 2y + 4z − 1 = 0
¸˜ e ´
A equacao do plano tamb´ m e determinada se ao inv´ s de serem dados trˆ s pontos,
e e
forem dados um ponto P1 do plano e dois vetores paralelos ao plano, V = (v1 , v2 , v3 )
e W = (w1 , w2 , w3 ), desde que eles sejam n˜ o paralelos. Ou ainda se forem dados
a
dois pontos P1 e P2 do plano e um vetor paralelo ao plano V = (v1 , v2 , v3 ), j´ que
a
−→
neste caso podemos formar o vetor W = P1 P2 = (w1 , w2 , w3 ) que e tamb´ m paralelo
´ e
ao plano.
Nestes casos temos novamente pelo menos duas maneiras de encontrarmos a
equacao do plano. Uma delas e observando que o vetor N = V × W e um ve-
¸˜ ´ ´
tor normal ao plano. Desta forma temos um ponto do plano e um vetor nor-
´
mal ao plano. A outra e observando que temos trˆ s vetores paralelos ao plano:
e
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

231. 4.1 ¸˜
Equacoes de Retas e Planos 219
−→
P1 P= ( x − x1 , y − y1 , z − z1 ), V e W. Como vimos anteriormente (Corol´ rio 3.9 na
a
p´ gina 191), os trˆ s vetores s˜ o coplanares se, e somente se, o produto misto entre
a e a
´
eles e zero, ou seja,
 
−→ x − x1 y − y1 z − z1
P1 P · (V × W ) = det  v1 v2 v3  = 0 . (4.3)
w1 w2 w3
Assim, um ponto P = ( x, y, z) pertence a um plano π que passa pelo ponto P1 =
( x1 , y1 , z1 ) e e paralelo aos vetores V = (v1 , v2 , v3 ) e W = (w1 , w2 , w3 ) (n˜ o paralelos)
´ a
¸˜ ´
se, e somente se, a equacao (4.3) e verdadeira.
Observa¸ ao. N˜ o faz sentido dizer que um vetor pertence a um plano. Pois, por um lado, um plano e um
c˜ a ´
conjunto de pontos e por outro, os vetores s˜ o “livres”, podem ser “colocados” em qualquer ponto. O correto
a
´ ´
e dizer que um vetor e paralelo a um plano.
¸˜
Equacoes Param´ tricas
e
e ¸˜
Al´ m da equacao geral do plano podemos tamb´ m caracterizar os pontos de um
e
plano da seguinte forma. Considere um plano π, um ponto P0 = ( x0 , y0 , z0 )
pertencente a π e dois vetores V = (v1 , v2 , v3 ) e W = (w1 , w2 , w3 ) n˜ o colinea-
a
res, paralelos a π. Um ponto P = ( x, y, z) pertence a π se, e somente se, o vetor
−→
P0 P= ( x − x0 , y − y0 , z − z0 ) e uma combinacao linear de V e W (Corol´ rio 3.10 na
´ ¸˜ a
p´ gina 192), ou seja, se existem escalares t e s tais que
a
−→
P0 P= tV + sW. (4.4)
Marco 2012
¸ Reginaldo J. Santos

232. 220 Retas e Planos
Escrevendo em termos de componentes (4.4) pode ser escrito como
( x − x0 , y − y0 , z − z0 ) = (tv1 + sw1 , tv2 + sw2 , tv3 + sw3 ).
Logo um ponto P = ( x, y, z) pertence a π se, e somente se, satisfaz as equacoes
¸˜

 x = x 0 + v 1 t + w1 s
y = y 0 + v 2 t + w2 s para t, s ∈ R.
z = z 0 + v 3 t + w3 s

¸˜
Estas equacoes s˜ o chamadas equa¸ oes param´ tricas do plano.
a c˜ e
Exemplo 4.3. Podemos obter equacoes param´ tricas do plano do Exemplo 4.2 na
¸˜ e
p´ gina 217 usando o fato de que ele passa pelo ponto P1 = (1/2, 0, 0) e e paralelo
a ´
−→ −→
aos vetores P1 P2 = (−1/2, 1/2, 0), P1 P3 = (−1/2, −1/2, 1/2). Assim,
1
 x = 2 − 1t − 1s

 2 2
y = 1t − 1s
2 2 para t, s ∈ R.

1
z = 2s

Exemplo 4.4. Para encontrarmos as equacoes param´ tricas do plano do Exemplo 4.1
¸˜ e
na p´ gina 212 podemos resolver a equacao geral do plano 2x + 2y + 4z − 1 = 0.
a ¸˜
Podemos proceder como no caso de sistemas lineares e considerar as vari´ veis y e z
a
livres: z = t e y = s. Assim, x = 1 − 2 t − s e portanto
2
 x = 1 −2t− s

2
y = s para t, s ∈ R.
z = t

¸˜ ¸˜
s˜ o equacoes param´ tricas do plano. Destas equacoes obtemos que os vetores
a e
V1 = (−2, 0, 1) e V2 = (−1, 1, 0) s˜ o paralelos ao plano.
a
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

233. 4.1 ¸˜
Equacoes de Retas e Planos 221
z z
r r
−→
OP
P = ( x, y, z)
−→
P0 P
V = ( a, b, c) −→
P0 = ( x0 , y0 , z0 ) OP0 V
x y x y
Figura 4.9 – Reta paralela ao vetor V = ( a, b, c)
Marco 2012
¸ Reginaldo J. Santos

234. 222 Retas e Planos
¸˜
4.1.2 Equacoes da Reta
¸˜
Equacoes Param´ tricas
e
Vamos supor que uma reta r seja paralela a um vetor V = ( a, b, c) n˜ o nulo e que
a
passe por um ponto P0 = ( x0 , y0 , z0 ). Um ponto P = ( x, y, z) pertence a reta r se, e
−→ −→
somente se, o vetor P0 P e paralelo ao vetor V, isto e, se o vetor P0 P e um multiplo
´ ´ ´ ´
escalar de V, ou seja,
−→
P0 P= t V . (4.5)
¸˜
Em termos de componentes, a equacao (4.5) pode ser escrita como
( x − x0 , y − y0 , z − z0 ) = (ta, tb, tc).
Logo, x − x0 = t a, y − y0 = t b e z − z0 = t c.
Ou seja, a reta r pode ser descrita como sendo o conjunto dos pontos P = ( x, y, z)
tais que

 x = x0 + t a
y = y0 + t b, para t ∈ R. (4.6)
z = z0 + t c

As equacoes (4.6), chamadas equa¸ oes param´ tricas da reta, s˜ o de uma reta r que
¸˜ c˜ e a
passa por um ponto P0 = ( x0 , y0 , z0 ) e e paralela ao vetor V = ( a, b, c), chamado
´
vetor diretor da reta r.
O parˆ metro t nas equacoes (4.6) pode ser interpretado como o instante de tempo,
a ¸˜
se o ponto P = ( x, y, z) descreve o movimento de uma part´cula em movimento
ı
retil´neo uniforme com vetor velocidade V = ( a, b, c). Observe que para t = 1, P =
ı
( x, y, z) = ( x0 + a, y0 + b, z0 + c), para t = 2, P = ( x, y, z) = ( x0 + 2a, y0 + 2b, z0 + 2c)
e assim por diante.
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

235. 4.1 ¸˜
Equacoes de Retas e Planos 223
¸˜
As equacoes (4.6), podem ser reescritas como
( x, y, z) = ( x0 + at, y0 + bt, z0 + ct),
que e chamada equa¸ ao vetorial da reta r.
´ c˜
Marco 2012
¸ Reginaldo J. Santos

236. 224 Retas e Planos
z
z0
a y0
x y
Figura 4.10 – Reta ( x, y, z) = ( x0 + at, y0 , z0 )
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

237. 4.1 ¸˜
Equacoes de Retas e Planos 225
z
z0
x0
b
x y
Figura 4.11 – Reta ( x, y, z) = ( x0 , y0 + bt, z0 )
Marco 2012
¸ Reginaldo J. Santos

238. 226 Retas e Planos
z
c
x0
y0
x y
Figura 4.12 – Reta ( x, y, z) = ( x0 , y0 , z0 + ct)
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

239. 4.1 ¸˜
Equacoes de Retas e Planos 227
z
z0
x y
Figura 4.13 – Reta ( x, y, z) = ( x0 + at, y0 + bt, z0 )
Marco 2012
¸ Reginaldo J. Santos

240. 228 Retas e Planos
z
x0
x y
Figura 4.14 – Reta ( x, y, z) = ( x0 , y0 + bt, z0 + ct)
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

241. 4.1 ¸˜
Equacoes de Retas e Planos 229
z
y0
x y
Figura 4.15 – Reta ( x, y, z) = ( x0 + at, y0 , z0 + ct)
Marco 2012
¸ Reginaldo J. Santos

242. 230 Retas e Planos
z
c
b
a
x y
Figura 4.16 – Reta ( x, y, z) = ( at, bt, ct)
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

243. 4.1 ¸˜
Equacoes de Retas e Planos 231
z
x y
Figura 4.17 – Reta ( x, y, z)=( x0+at, y0+bt, z0+ct)
Marco 2012
¸ Reginaldo J. Santos

244. 232 Retas e Planos
c˜ a a ´
Observa¸ ao. N˜ o faz sentido dizer que o vetor est´ contido na reta. Por um lado, a reta e um conjunto de
¸˜
pontos e por outro um vetor n˜ o tem posicao fixa.
a
Exemplo 4.5. A reta que passa por P0 = (−3, 3/2, 4) e e paralela ao vetor V =
´
(−6, 1, 4) tem equacoes param´ tricas
¸˜ e

 x = −3 − 6 t
r: 3 para t ∈ R
y = 2 +t
z = 4 + 4t

Podemos encontrar a intersecao da reta r com os planos coordenados xy, yz e xz. A
¸˜
equacao do plano xy e z = 0, do plano yz e x = 0 e do plano xz e y = 0. Substituindo
¸˜ ´ ´ ´
z = 0 nas equacoes de r, obtemos t = −1, x = 3 e y = 1/2, ou seja,
¸˜
• o ponto de intersecao de r com o plano xy e
¸˜ ´
1
( x, y, z) = (3, , 0).
2
De forma an´ loga obtemos
a
• o ponto de intersecao de r com o plano yz e
¸˜ ´
( x, y, z) = (0, 1, 2),
• o ponto de intersecao de r com o plano xz
¸˜
( x, y, z) = (6, 0, −2).
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

245. 4.1 ¸˜
Equacoes de Retas e Planos 233
z
2
1/2
1
3
x y
Figura 4.18 – Reta que passa pelo ponto P0 = (−3, 3/2, 4) paralela ao vetor V = (−6, 1, 4)
Marco 2012
¸ Reginaldo J. Santos

246. 234 Retas e Planos
¸˜
Equacoes na Forma Sim´ trica
e
Se todas componentes do vetor diretor da reta r s˜ o n˜ o nulos, podemos resolver
a a
cada equacao em (4.6) para t e igualar os resultados obtendo o que chamamos de
¸˜
equa¸ oes na forma sim´ trica de r:
c˜ e
x − x0 y − y0 z − z0
= = .
a b c
No Exemplo 4.5 as equacoes de r na forma sim´ trica s˜ o:
¸˜ e a
x+3 y − 3/2 z−4
= = .
−6 1 4
Exemplo 4.6. Vamos encontrar as equacoes param´ tricas da reta r que passa pelos
¸˜ e
pontos P1 = (3, 0, 2) e P2 = (0, 3, 3). O vetor
−→
P1 P2 = (0 − 3, 3 − 0, 3 − 2) = (−3, 3, 1)
e paralelo a r e o ponto P1 = (3, 0, 2) pertence a r. Portanto, as equacoes param´ tricas
´ ¸˜ e
de r s˜ o
a 
 x = 3−3t
y = 3t para t ∈ R.
z = 2+t

Exemplo 4.7. Vamos encontrar as equacoes param´ tricas da reta r, intersecao dos
¸˜ e ¸˜
planos
π1 : 2x + y + 4z − 4 = 0
π2 : 2x − y + 2z = 0.
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

247. 4.1 ¸˜
Equacoes de Retas e Planos 235
z
3
P2
2
P1
r
3 3
x y
Figura 4.19 – Reta que passa pelos pontos P1 = (3, 0, 2) e P2 = (0, 3, 3)
Marco 2012
¸ Reginaldo J. Santos

248. 236 Retas e Planos
z
1
2
4
y
x
Figura 4.20 – π1 : 2x + y + 4z − 4 = 0
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

249. 4.1 ¸˜
Equacoes de Retas e Planos 237
z
5/2
5/2
5
y
x
Figura 4.21 – π2 : 2x − y + 2z = 0
Marco 2012
¸ Reginaldo J. Santos

250. 238 Retas e Planos
z
5/2
1
5/2 2
4
5
y
x
Figura 4.22 – π1 , π2 e π1 ∩ π2
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

251. 4.1 ¸˜
Equacoes de Retas e Planos 239
Vetores normais destes planos s˜ o
a
N1 = (2, 1, 4) e N2 = (2, −1, 2) .
A reta r est´ contida em ambos os planos, portanto e perpendicular a ambos os veto-
a ´
res normais. Assim, a reta r e paralela ao produto vetorial N1 × N2 (Teorema 3.5 (c)
´
na p´ gina 179).
a
1 4 2 4 2 1
N1 × N2 = det , − det , det = (6, 4, −4) .
−1 2 2 2 2 −1
Assim, V = N1 × N2 = (6, 4, −4) e um vetor diretor de r. Agora, precisamos encon-
´
trar um ponto da reta r. Este ponto e uma solucao particular do sistema
´ ¸˜
2x + y + 4z − 4 = 0
(4.7)
2x − y + 2z =0
¸˜
Para encontrar uma solucao particular do sistema, atribu´mos um valor a uma das
ı
incognitas (neste exemplo podemos fazer x = 0) e resolvemos o sistema obtido, que
´
´ ¸˜ ´
e de duas equacoes e duas incognitas
y + 4z − 4 = 0
−y + 2z =0
Obtemos ent˜ o, y = 4/3 e z = 2/3, ou seja, o ponto P0 = (0, 4/3, 2/3) e um ponto
a ´
da reta r, pois e uma solucao particular do sistema (4.7). Assim, as equacoes pa-
´ ¸˜ ¸˜
ram´ tricas de r s˜ o
e a

 x = 6t
y = 4/3 + 4t para todo t ∈ R. (4.8)
z = 2/3 − 4t

Alternativamente, podemos encontrar as equacoes param´ tricas de r determinando
¸˜ e
¸˜
a solucao geral do sistema (4.7). Para isto devemos escalonar a matriz do sistema
Marco 2012
¸ Reginaldo J. Santos

252. 240 Retas e Planos
(4.7):
2 1 4 4
2 −1 2 0
Precisamos “zerar” o outro elemento da 1a coluna, que e a coluna do pivo, para isto,
. ´ ˆ
` 2a linha, menos a 1a linha.
adicionamos a . .
2 1 4 4
-1a linha + 2a linha −→ 2a linha
. . .
0 −2 −2 −4
¸˜ ´
Agora, j´ podemos obter facilmente a solucao geral do sistema dado, j´ que ele e
a a
equivalente ao sistema
2x + y + 4z = 4
− 2y − 2z = −4
A vari´ vel z e uma vari´ vel livre. Podemos dar a ela um valor arbitr´ rio, digamos t,
a ´ a a
para t ∈ R qualquer. Assim, a solucao geral do sistema dado e
¸˜ ´
3

 x = 1 − 2t
y = 2 − t para todo t ∈ R. (4.9)
z = t

¸˜ ¸˜
Estas equacoes s˜ o diferentes das equacoes (4.8), mas representam a mesma reta,
a
pois os vetores diretores obtidos das duas equacoes s˜ o paralelos e o ponto P0 =
¸˜ a
(1, 2, 0) satisfaz tamb´ m as equacoes (4.9). Poder´amos dizer tamb´ m que (4.8) e
e ¸˜ ı e
(4.9) representam retas coincidentes.
´ ¸˜ ´
O proximo exemplo mostra como encontrar a equacao da reta que e perpendicular a
duas retas.
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

253. 4.1 ¸˜
Equacoes de Retas e Planos 241
Exemplo 4.8. Achar as equacoes da reta r3 que intercepta as retas
¸˜

 x = −1 + 2t
r1 : y = 1 + t, para todo t ∈ R
z = 0

e
y−4
r2 : x − 2 = e z=3
2
´
e e perpendicular a ambas.
Um ponto qualquer da reta r1 e descrito por Pr1 = (−1 + 2t, 1 + t, 0) e um ponto
´
qualquer da reta r2 e da forma Pr2 = (2 + s, 4 + 2s, 3). Aqui e necess´ rio o uso de um
´ ´ a
−→
parˆ metro diferente para a reta r2 . O vetor Pr1 Pr2 = (3 + s − 2t, 3 + 2s − t, 3) “liga”
a
um ponto qualquer de r1 a um ponto qualquer de r2 . Vamos determinar t e s tais
−→
que o vetor Pr1 Pr2 seja perpendicular ao vetor diretor V1 = (2, 1, 0) de r1 e ao vetor
diretor V2 = (1, 2, 0) de r2 , ou seja, temos que resolver o sistema
−→
Pr1 Pr2 ·V1 = 9 + 4s − 5t = 0
−→
Pr1 Pr2 ·V2 = 9 + 5s − 4t = 0
A solucao deste sistema e t = 1, s = −1. Logo Pr1 = (1, 2, 0), Pr2 = (1, 2, 3) e
¸˜ ´
−→
V3 = Pr1 Pr2 = (0, 0, 3). Assim as equacoes param´ tricas da reta procurada s˜ o
¸˜ e a

 x = 1
r3 : y = 2, para todo t ∈ R.
z = 3t

¸˜ ´
Esta solucao usou o fato de que as retas s˜ o reversas, isto e, elas n˜ o s˜ o paralelas,
a a a
e a ¸˜
mas tamb´ m n˜ o se interceptam. Como seria a solucao se elas se interceptassem?
Por exemplo se a reta r2 fosse dada por
y−4
r2 : x − 2 = e z=0?
2
Marco 2012
¸ Reginaldo J. Santos

254. 242 Retas e Planos
Exerc´cios Num´ ricos (respostas na p´ gina 556)
ı e a
4.1.1. Faca um esboco dos seguintes planos:
¸ ¸
(a) 2x + 3y + 5z − 1 = 0 (e) 3x + 2y − 1 = 0
(b) x − 2y + 4z = 0 (f) 5y − 2 = 0
(c) 3y + 2z − 1 = 0 (g) 3z − 2 = 0
(d) 2x + 3z − 1 = 0 (h) 2x − 1 = 0
4.1.2. Faca um esboco das retas dadas a seguir:
¸ ¸
3 1
(a) ( x, y, z) = (−3 + 3t, − t, 4 − 2t) (e) ( x, y, z) = (2 + 2t, 3 + t, 3)
2 2
3 (f) ( x, y, z) = (1, 2, 2 + 2t)
(b) ( x, y, z) = (2t, t, t)
2 (g) ( x, y, z) = (1, 2 + 2t, 3)
(c) ( x, y, z) = (1 + t, 2, 3 + 2t) (h) ( x, y, z) = (2 + 2t, 2, 3)
(d) ( x, y, z) = (1, 2 + 2t, 5 + 3 t)
2 2
4.1.3. Ache a equacao do plano paralelo ao plano 2x − y + 5z − 3 = 0 e que passa por P = (1, −2, 1).
¸˜
4.1.4. Encontre a equacao do plano que passa pelo ponto P = (2, 1, 0) e e perpendicular aos planos x + 2y −
¸˜ ´
3z + 2 = 0 e 2x − y + 4z − 1 = 0.
4.1.5. Encontrar a equacao do plano que passa pelos pontos P = (1, 0, 0) e Q = (1, 0, 1) e e perpendicular ao
¸˜ ´
plano y = z.
4.1.6. Determine a intersecao da reta que passa pela origem e tem vetor diretor V = i + 2 j + k com o plano
¸˜
2x + y + z = 5.
4.1.7. Verifique se as retas r : ( x, y, z) = (9t, 1 + 6t, −2 + 3t) e s : ( x, y, z) = (1 + 2t, 3 + t, 1) se interceptam e
¸˜ a ´ ´
em caso afirmativo determine a intersecao. (Sugest˜ o: a quest˜ o e se as trajetorias se cortam e n˜ o se as
a a
part´culas se chocam, ou seja, elas n˜ o precisam estar num ponto no mesmo instante.)
ı a
4.1.8. Dadas as retas
x−2 y
r: = =z e s : x−2 = y = z,
2 2
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

255. 4.1 ¸˜
Equacoes de Retas e Planos 243
obtenha uma equacao geral para o plano determinado por r e s.
¸˜
4.1.9. Sejam P = (4, 1, −1) e r : ( x, y, z) = (2 + t, 4 − t, 1 + 2t).
(a) Mostre que P ∈ r;
(b) Obtenha uma equacao geral do plano determinado por r e P.
¸˜
4.1.10. Dados os planos π1 : x − y + z + 1 = 0 e π2 : x + y − z − 1 = 0, determine o plano que cont´ m π1 ∩ π2
e
e e ortogonal ao vetor (−1, 1, −1).
´
4.1.11. Quais dos seguintes pares de planos se cortam segundo uma reta?
(a) x + 2y − 3z − 4 = 0 e x − 4y + 2z + 1 = 0;
(b) 2x − y + 4z + 3 = 0 e 4x − 2y + 8z = 0;
(c) x − y = 0 e x + z = 0.
4.1.12. Encontre as equacoes da reta que passa pelo ponto Q = (1, 2, 1) e e perpendicular ao plano x − y + 2z −
¸˜ ´
1 = 0.
4.1.13. Ache equacoes da reta que passa pelo ponto P = (1, 0, 1) e e paralela aos planos 2x + 3y + z + 1 = 0 e
¸˜ ´
x − y + z = 0.
4.1.14. Seja r a reta determinada pela intersecao dos planos x + y − z = 0 e 2x − y + 3z − 1 = 0. Ache a equacao
¸˜ ¸˜
do plano que passa por A = (1, 0, −1) e cont´ m a reta r.
e
4.1.15. Sejam r e s retas reversas passando por A = (0, 1, 0) e B = (1, 1, 0) e por C = (−3, 1, −4) e D =
(−1, 2, −7), respectivamente. Obtenha uma equacao da reta concorrente com r e s e paralela ao vetor
¸˜
V = (1, −5, −1).
4.1.16. (a) Mostre que os planos 2x − y + z = 0 e x + 2y − z = 1 se interceptam segundo uma reta r;
(b) Ache equacoes da reta que passa pelo ponto A = (1, 0, 1) e intercepta a reta r ortogonalmente.
¸˜
4.1.17. Considere as retas ( x, y, z) = t(1, 2, −3) e ( x, y, z) = (0, 1, 2) + s(2, 4, −6). Encontre a equacao geral do
¸˜
plano que cont´ m estas duas retas.
e
Marco 2012
¸ Reginaldo J. Santos

256. 244 Retas e Planos
¸˜ ¸˜
4.1.18. Determine as equacoes param´ tricas da reta intersecao dos planos:
e
(a) x + 2y − 3z − 4 = 0 e x − 4y + 2z + 1 = 0;
(b) x − y = 0 e x + z = 0.
4.1.19. Considere o plano π : 2x + 2y − z = 0.
(a) Determine as retas r, intersecao do plano π com o plano yz, s, intersecao do plano π com o plano xz
¸˜ ¸˜
e t, intersecao do plano π com o plano z = 2. Desenhe um esboco do plano π mostrando as retas r,
¸˜ ¸
s e t.
(b) Determine o volume do tetraedro determinado pelo plano π, os planos coordenados xz e yz e o
plano z = 2. (Sugest˜ o: este volume e igual a 1/6 do volume do paralelep´pedo determinado por
a ´ ı
−→ −→ −→
OA, OB e OC, em que O = (0, 0, 0), A e o ponto intersecao do eixo z com o plano z = 2, B e a
´ ¸˜ ´
intersecao das retas r e t e C e a intersecao das retas s e t.)
¸˜ ´ ¸˜
´
(c) Determine a area da face do tetraedro contida no plano π.
(d) Determine a altura do tetraedro relativa a face contida no plano π. (Sugest˜ o: a reta ortogonal ao
a
plano π que passa pelo ponto A intercepta o plano π num ponto P de forma que a altura procurada
−→
e igual a || AP ||)
´
4.1.20. Achar as equacoes da reta que intercepta as retas r1 e r2 e e perpendicular a ambas.
¸˜ ´
(a)

 x = 1+t
r1 : y = 2 + 3t, para t ∈ R
z = 4t

e
y−1 z+2
r2 : x + 1 = = .
2 3
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

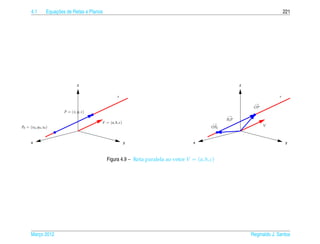
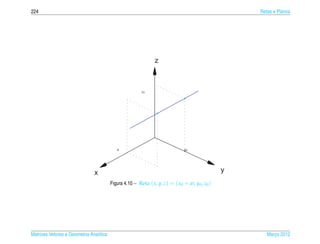
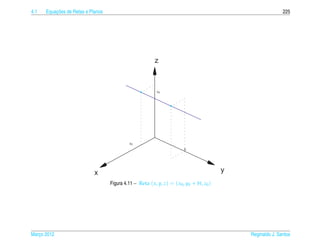
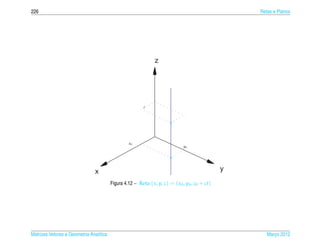
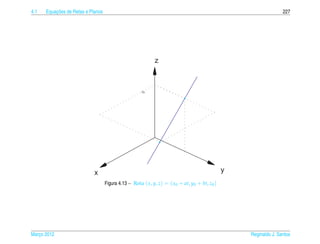
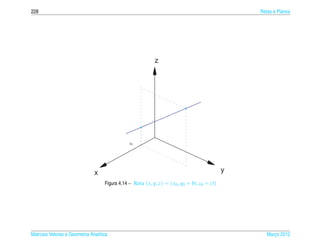
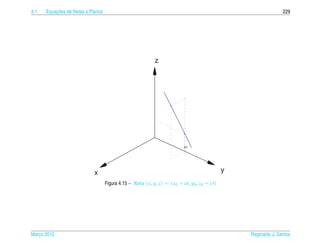
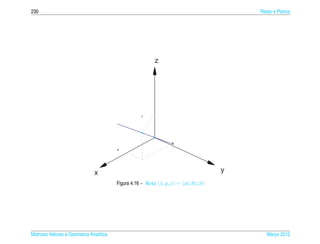
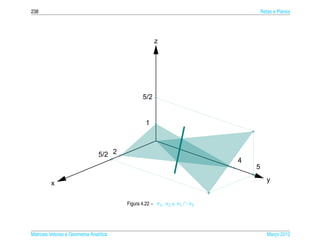
257. 4.1 ¸˜
Equacoes de Retas e Planos 245
(b) 
 x = −1 + t
r1 : y = 2 + 3t, para t ∈ R
z = 4t

e
y−4 z−3
r2 : x = = .
2 3
Exerc´cios usando o M ATLAB
ı
>> V=[v1,v2,v3] cria um vetor V, usando as componentes num´ ricas v1, v2, v3. Por exemplo >>
e
V=[1,2,3] cria o vetor V = (1, 2, 3);
´ ´ ´
>> V+W e a soma de V e W; >> V-W e a diferenca V menos W; >> num*V e o produto do vetor V pelo escalar
¸
num;
>> subs(expr,x,num,) substitui x por num na express˜ o expr;
a
¸˜ ¸˜
>> solve(expr) determina a solucao da equacao expr=0;
Comandos num´ ricos do pacote GAAL:
e
>> no(V) calcula a norma do vetor V.
>> pe(V,W) calcula o produto escalar do vetor V pelo vetor W.
>> pv(V,W) calcula o produto vetorial do vetor V pelo vetor W.
>> subst(expr,[x,y,z],[a,b,c]) substitui na express˜ o expr as vari´ veis x,y,z por a,b,c, respecti-
a a
vamente.
Comandos gr´ ficos do pacote GAAL:
a
¸˜
>> lin(P,V) desenha a reta que passa por P com direcao V.
Marco 2012
¸ Reginaldo J. Santos

258. 246 Retas e Planos
¸˜
>> lin(P1,V1,P2,V2) desenha retas que passam por P1, P2, direcoes V1, V2.
>> plan(P,N) desenha o plano que passa por P com normal N.
>> plan(P1,N1,P2,N2) desenha planos que passam por P1, P2, normais N1, N2.
>> plan(P1,N1,P2,N2,P3,N3) desenha planos que passam por P1, P2 e P3 com normais N1, N2 e N3.
>> poplan(P1,P2,N2) desenha ponto P1 e plano passando por P2 com normal N2.
¸˜
>> poline(P1,P2,V2) desenha ponto P2 e reta passando por P2 com direcao V2.
¸˜
>> lineplan(P1,V1,P2,N2) desenha reta passando por P1 com direcao V1 e plano passando por P2 com
normal N2.
>> axiss reescala os eixos com a mesma escala.
>> rota faz uma rotacao em torno do eixo z.
¸˜
¸˜ ¸˜ ¸˜
4.1.21. Digite no prompt demog22, (sem a v´rgula!). Esta funcao demonstra as funcoes gr´ ficas para visualizacao
ı a
de retas e planos.
4.1.22. Use o M ATLAB para resolver os Exerc´cios Num´ ricos
ı e
Exerc´cio Teorico
ı ´
4.1.23. Seja ax + by + cz + d = 0 a equacao de um plano π com abcd = 0.
¸˜
¸˜
(a) Determine a intersecao de π com os eixos;
(b) Se P1 = ( p1 , 0, 0), P2 = (0, p2 , 0) e P3 = (0, 0, p3 ) s˜ o as intersecoes de π com os eixos, a equacao de
a ¸˜ ¸˜
π pode ser posta sob a forma
x y z
+ + = 1.
p1 p2 p3
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

259. 4.1 ¸˜
Equacoes de Retas e Planos 247
z z z
3 3
3/2 1 3/22
3 3 3 3 3
6 6
x y x y x y
Figura 4.23 – Retas r1 , r2 e r3 do Exemplo 4.8
Marco 2012
¸ Reginaldo J. Santos

260. 248 Retas e Planos
ˆ
4.2 Angulos e Distˆ ncias
a
ˆ
4.2.1 Angulos
ˆ
Angulo entre Retas
Com duas retas no espaco pode ocorrer um dos seguintes casos:
¸
(a) As retas se interceptam em um ponto, ou seja, s˜ o concorrentes;
a
(b) As retas s˜ o paralelas (ou coincidentes);
a
a ´ a a
(c) As retas s˜ o reversas, isto e, n˜ o s˜ o paralelas mas tamb´ m n˜ o se interceptam.
e a
ˆ
Se as retas se interceptam, ent˜ o elas determinam quatro angulos, dois a dois opostos
a
ˆ ´ ˆ
pelo v´ rtice. O angulo entre elas e definido como sendo o menor destes angulos.
e
Se as retas r1 e r2 s˜ o reversas, ent˜ o por um ponto P de r1 passa um reta r2 que e
a a ´
paralela a r2 . O angulo entre r1 e r2 e definido como sendo o angulo entre r1 e r2
ˆ ´ ˆ
(Figura 4.24).
ˆ ´
Se as retas s˜ o paralelas o angulo entre elas e igual a zero.
a
Em qualquer dos casos, se V1 e V2 s˜ o vetores paralelos a r1 e r2 respectivamente,
a
ˆ
ent˜ o o cosseno do angulo entre elas e
a ´
cos(r1 , r2 ) = | cos θ | ,
em que θ e o angulo entre V1 e V2 .
´ ˆ
¸˜ ¸˜
Lembrando que da definicao de produto escalar (Definicao 3.1 na p´ gina 166), pode-
a
ˆ
mos encontrar o cosseno do angulo entre dois vetores, ou seja,
V1 · V2
cos θ = .
||V1 || ||V2 ||
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

261. 4.2 ˆ
Angulos e Distˆ ncias
a 249
z
r2
r2
V2
θ
x P V1 y
r1
ˆ
Figura 4.24 – O Angulo entre duas retas reversas r1 e r2
Marco 2012
¸ Reginaldo J. Santos

262. 250 Retas e Planos
Isto prova o resultado seguinte.
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

263. 4.2 ˆ
Angulos e Distˆ ncias
a 251
¸˜
Proposicao 4.2. Sejam duas retas
 
 x = x1 + t a1  x = x2 + t a2
r1 : y = y1 + t b1 r2 : y = y2 + t b2 para todo t ∈ R.
z = z1 + t c1 z = z2 + t c2
 
O cosseno do angulo entre r1 e r2 e
ˆ ´
|V1 · V2 |
cos(r1 , r2 ) = | cos θ | = ,
||V1 || ||V2 ||
em que V1 = ( a1 , b1 , c1 ) e V2 = ( a2 , b2 , c2 ).
Exemplo 4.9. Encontrar o angulo entre a reta
ˆ
x + y − z + 1 = 0
r1 :
2x − y + z = 0
e a reta 
 x = 2t
r2 : y = 1−t para todo t ∈ R.
z = 2+3t

Vamos encontrar vetores paralelos a estas retas. A reta r1 e dada como a intersecao
´ ¸˜
de dois planos, portanto o produto vetorial dos vetores normais dos dois planos e ´
paralelo a r1 .
N1 = (1, 1, −1),
N2 = (2, −1, 1),
Marco 2012
¸ Reginaldo J. Santos

264. 252 Retas e Planos
1 −1 1 −1 1 1
V1 = N1 × N2 = det , − det , det = (0, −3, −3)
−1 1 2 1 2 −1
e paralelo a r1 e V2 = (2, −1, 3) e paralelo a r2 . Assim,
´ ´
|V1 · V2 | |0 · 2 + (−3)(−1) + (−3) · 3|
cos(r1 , r2 ) = =
||V1 || ||V2 || 02 + (−3)2 + (−3)2 · 22 + (−1)2 + 32
| − 6| 1
= √ √ = √ .
18 · 14 7
Portanto, o angulo entre r1 e r2 e
ˆ ´
1
arccos ( √ ) ≈ 67o .
7
ˆ
Angulo entre Planos
Sejam π1 e π2 dois planos com vetores normais N1 = ( a1 , b1 , c1 ) e N2 = ( a2 , b2 , c2 ),
ˆ ´ ˆ
respectivamente. O angulo entre π1 e π2 e definido como o angulo entre duas retas
perpendiculares a eles. Como toda reta perpendicular a π1 tem N1 como vetor di-
retor e toda reta perpendicular a π2 tem N2 como vetor diretor, ent˜ o o cosseno do
a
ˆ ´
angulo entre eles e dado por
cos(π1 , π2 ) = | cos θ | ,
em que θ e o angulo entre os vetores normais N1 e N2 de π1 e π2 , respectivamente
´ ˆ
(Figura 4.25).
| N1 · N2 |
Portanto, o cosseno do angulo entre π1 e π2 e cos(π1 , π2 ) =
ˆ ´ . O que
|| N1 || || N2 ||
prova o resultado seguinte.
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

265. 4.2 ˆ
Angulos e Distˆ ncias
a 253
¸˜
Proposicao 4.3. Sejam dois planos
π1 : a1 x + b1 y + c1 z + d1 = 0,
π2 : a2 x + b2 y + c2 z + d2 = 0.
O cosseno do angulo entre π1 e π2 e
ˆ ´
| N1 · N2 |
cos(π1 , π2 ) = ,
|| N1 || || N2 ||
em que N1 = ( a1 , b1 , c1 ) e N2 = ( a2 , b2 , c2 ) s˜ o os vetores normais de π1 e π2 , respectivamente.
a
Marco 2012
¸ Reginaldo J. Santos

266. 254 Retas e Planos
N1
N2
θ
π2
θ
π1
ˆ
Figura 4.25 – Angulo entre dois planos
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

267. 4.2 ˆ
Angulos e Distˆ ncias
a 255
Dois planos π1 e π2 ou s˜ o paralelos ou se cortam segundo um reta. Eles s˜ o parale-
a a
´
los se, e somente se, os vetores normais de π1 e π2 , s˜ o paralelos, ou seja, um vetor e
a
´ ˆ
um multiplo escalar do outro. Assim, π e π2 s˜ o paralelos se, e somente se, o angulo
a
´
entre eles e igual a zero.
Exemplo 4.10. Determinar o angulo entre os planos cujas equacoes s˜ o
ˆ ¸˜ a
π1 : x+y+z = 0,
π2 : x − y − z = 0.
Os vetores normais a estes planos s˜ o os vetores cujas componentes s˜ o os coeficien-
a a
tes de x, y e z nas equacoes dos planos, ou seja,
¸˜
N1 = (1, 1, 1) e N2 = (1, −1, −1) .
ˆ ´
Assim, o cosseno do angulo entre π1 e π2 e
| N1 · N2 | 1 1
cos(π1 , π2 ) = = √ √ = .
|| N1 || || N2 || 3· 3 3
ˆ ´
Portanto, o angulo entre eles e
1
arccos ( ) ≈ 70o .
3
4.2.2 Distˆ ncias
a
Distˆ ncia de Um Ponto a Um Plano
a
Sejam P0 = ( x0 , y0 , z0 ) um ponto qualquer e π : ax + by + cz + d = 0 um plano. A
distˆ ncia de P0 a π e definida como sendo a distˆ ncia de P0 at´ o ponto de π mais
a ´ a e
proximo de P0 .
´
Marco 2012
¸ Reginaldo J. Santos

268. 256 Retas e Planos
−→
Dado um ponto P1 = ( x1 , y1 , z1 ) de π, podemos decompor o vetor P1 P0 em duas
parcelas, uma na direcao do vetor normal de π, N = ( a, b, c) e outra perpendicular
¸˜
−→
a ele. A componente na direcao do vetor N e a projecao ortogonal de P1 P0 em N.
¸˜ ´ ¸˜
Como vemos na Figura 4.26, a distˆ ncia de P0 a π e igual a norma da projecao, ou
a ´ ` ¸˜
seja,
−→
dist( P0 , π ) = ||proj N P1 P0 || .
¸˜
Mas, pela Proposicao 3.4 na p´ gina 174, temos que
a
 −→  −→
−→ P1 P0 · N  | P1 P0 · N |
||proj N P1 P0 || =  N = .
|| N ||2 || N ||
O que prova o resultado seguinte.
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

269. 4.2 ˆ
Angulos e Distˆ ncias
a 257
P0 = ( x0 , y0 , z0 )
dist( P0 , π )
proj N P1 P0
N = ( a, b, c)
−→
P1 = ( x1 , y1 , z1 )
π
Figura 4.26 – Distˆ ncia de um ponto P0 = ( x0 , y0 , z0 ) a um plano π
a
Marco 2012
¸ Reginaldo J. Santos

270. 258 Retas e Planos
¸˜
Proposicao 4.4. Sejam P0 = ( x0 , y0 , z0 ) um ponto qualquer e π : ax + by + cz + d = 0 um plano. A distˆ ncia de P0
a
a π e dada por
´
−→
−→ | P P ·N|
dist( P0 , π ) = ||proj N P1 P0 || = 1 0 ,
|| N ||
em que N = ( a, b, c) e P1 = ( x1 , y1 , z1 ) e um ponto de π (isto e, um ponto que satisfaz a equa¸ ao de π).
´ ´ c˜
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

271. 4.2 ˆ
Angulos e Distˆ ncias
a 259
Exemplo 4.11. Calcular a distˆ ncia entre o ponto P0 = (1, 2, 3) ao plano
a
π : x − 2y + z − 1 = 0.
Fazendo z = 0 e y = 0 na equacao de π, obtemos x = 1. Assim, o ponto P1 = (1, 0, 0)
¸˜
pertence a π.
−→
P1 P0 = (1 − 1, 2 − 0, 3 − 0) = (0, 2, 3)
e
N = (1, −2, 1) .
Assim,
−→
−→ | P P ·N| |0 · 1 + 2(−2) + 3 · 1| | − 1| 1
dist( P0 , π ) = ||proj N P1 P0 || = 1 0 = = √ = √ .
|| N || 1 2 + (−2)2 + 12 6 6
Distˆ ncia de Um Ponto a Uma Reta
a
Sejam P0 = ( x0 , y0 , z0 ) um ponto qualquer e r uma reta. A distˆ ncia de P0 a r e
a ´
definida como a distˆ ncia de P0 ao ponto de r mais proximo de P0 .
a ´
−→
Dado um ponto qualquer P1 = ( x1 , y1 , z1 ) de r podemos decompor o vetor P1 P0 em
duas parcelas, uma na direcao do vetor diretor V de r e outra perpendicular a ele.
¸˜
−→
A componente na direcao do vetor V e a projecao ortogonal de P1 P0 em V. Como
¸˜ ´ ¸˜
vemos na Figura 4.27,
−→ −→
(dist( P0 , r ))2 + ||projV P1 P0 ||2 = || P1 P0 ||2 ,
ou seja,
−→ −→
(dist( P0 , r ))2 = || P1 P0 ||2 − ||projV P1 P0 ||2 . (4.10)
Marco 2012
¸ Reginaldo J. Santos

272. 260 Retas e Planos
P0 = ( x0 , y0 , z0 )
dist( P0 , r )
−→
r P1 = ( x1 , y1 , z1 ) projV P1 P0 V = ( a, b, c)
Figura 4.27 – Distˆ ncia de um ponto P0 = ( x0 , y0 , z0 ) a uma reta r
a
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

273. 4.2 ˆ
Angulos e Distˆ ncias
a 261
¸˜
Mas, pela Proposicao 3.4 na p´ gina 174, temos que
a
 −→  2 −→
−→ P1 P0 ·V  ( P P ·V )2
||projV P1 P0 ||2 =  V = 1 0 2 .
||V ||2 ||V ||
¸˜
Substituindo esta express˜ o em (4.10) e usando a definicao do produto escalar na
a
p´ gina 166 e da norma do produto vetorial na p´ gina 177 obtemos
a a
−→ −→ −→
−→ ( P P ·V )2 || P1 P0 ||2 ||V ||2 − ( P1 P0 ·V )2
(dist( P0 , r )) 2
= || P1 P0 || − 1 0 2 =
2
||V || ||V ||2
−→ −→
|| P1 P0 ||2 ||V ||2 − || P1 P0 ||2 ||V ||2 cos2 θ
=
||V ||2
−→ −→
|| P1 P0 ||2 ||V ||2 sen2 θ || P1 P0 ×V ||2
= 2
= .
||V || ||V ||2
Isto prova o resultado seguinte.
¸˜
Proposicao 4.5. Sejam P0 = ( x0 , y0 , z0 ) um ponto qualquer e

 x = x1 + t a
r : y = y1 + t b para todo t ∈ R
z = z1 + t c

uma reta. A distˆ ncia de P0 a r e dada por
a ´
−→
|| P1 P0 ×V ||
dist( P0 , r ) = .
||V ||
em que V = ( a, b, c) e um vetor diretor e P1 = ( x1 , y1 , z1 ) e um ponto da reta r.
´ ´
Marco 2012
¸ Reginaldo J. Santos

274. 262 Retas e Planos
Exemplo 4.12. Calcular a distˆ ncia do ponto P0 = (1, −1, 2) a reta
a `

 x = 1+2t
r : y = −t para todo t ∈ R.
z = 2−3t

Um vetor diretor da reta r e V = (2, −1, −3) e um ponto de r e P1 = (1, 0, 2). Assim,
´ ´
−→
P1 P0 = (1 − 1, −1 − 0, 2 − 2) = (0, −1, 0) ,
−→
P1 P0 ×V = (3, 0, 2) ,
−→ √ √
|| P1 P0 ×V || = 13 e ||V || = 14 .
Portanto,
−→
|| P1 P0 ×V || 13
dist( P0 , r ) = = .
||V || 14
Distˆ ncia entre Dois Planos
a
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

275. 4.2 ˆ
Angulos e Distˆ ncias
a 263
π2
P2
dist(π1 , π2 )
proj N1 P1 P2
−→
N1
π1
P1
Figura 4.28 – Distˆ ncia entre dois planos
a
Marco 2012
¸ Reginaldo J. Santos

276. 264 Retas e Planos
´
Sejam dois planos π1 e π2 quaisquer. A distˆ ncia entre π1 e π2 e definida como a
a
menor distˆ ncia entre dois pontos, um de π1 e outro de π2 .
a
Se os seus vetores normais n˜ o s˜ o paralelos, ent˜ o os planos s˜ o concorrentes e
a a a a
a ´
neste caso a distˆ ncia entre eles e igual a zero. Se os seus vetores normais s˜ o pa-
a
a a a ´
ralelos, ent˜ o os planos s˜ o paralelos (ou coincidentes) e a distˆ ncia entre π1 e π2 e
igual a distˆ ncia entre um ponto de um deles, por exemplo P2 de π2 , e o ponto de
` a
π1 , mais proximo de P2 (Figura 4.28). Mas, esta distˆ ncia e igual a distˆ ncia de P2 a
´ a ´ ` a
π1 . Vamos ver isto em um exemplo.
Exemplo 4.13. Os planos π1 : x + 2y − 2z − 3 = 0 e π2 : 2x + 4y − 4z − 7 = 0
s˜ o paralelos, pois os seus vetores normais N1 = (1, 2, −2) e N2 = (2, 4, −4) s˜ o
a a
´ ´
paralelos (um e multiplo escalar do outro). Vamos encontrar a distˆ ncia entre eles.
a
Vamos encontrar dois pontos quaisquer de cada um deles. Fazendo z = 0 e y = 0
em ambas as equacoes obtemos x1 = 3 e x2 = 7/2. Assim, P1 = (3, 0, 0) pertence a
¸˜
π1 e P2 = (7/2, 0, 0) pertence a π2 . Portanto, pela Proposicao 4.4 temos que
¸˜
−→
−→
| P P ·N |
dist(π1 , π2 ) = dist(π1 , P2 ) = || = 1 2 1
||proj N1 P1 P2
|| N1 ||
|(7/2 − 3, 0 − 0, 0 − 0) · (1, 2, −2)| |(1/2) · 1 + 0 · 2 + 0(−2)| 1
= = √ = .
1 2 + 22 + (−2)2 9 6
Distˆ ncia entre Duas Retas
a
Sejam r1 e r2 duas retas quaisquer. A distˆ ncia entre r1 e r2 e definida como a menor
a ´
distˆ ncia entre dois pontos, um de r1 e outro de r2 .
a
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

277. 4.2 ˆ
Angulos e Distˆ ncias
a 265
P2
r2
dist(r1 , r2 )
−→
r1 projV P1 P2
1
V1
P1
Figura 4.29 – Distˆ ncia entre duas retas paralelas
a
Marco 2012
¸ Reginaldo J. Santos

278. 266 Retas e Planos
Para calcular a distˆ ncia entre duas retas, vamos dividir em dois casos:
a
(a) Se os vetores diretores s˜ o paralelos, ent˜ o as retas r1 e r2 s˜ o paralelas (ou
a a a
´ `
coincidentes). Neste caso, a distˆ ncia entre elas e igual a distˆ ncia entre um
a a
ponto de r2 e a reta r1 , ou vice-versa, entre um ponto de r1 e a reta r2 (Figura
¸˜
4.29). Assim, pela Proposicao 4.5 na p´ gina 261, temos que
a
−→
|| P1 P2 ×V2 ||
dist(r1 , r2 ) = dist( P1 , r2 ) = , (4.11)
||V2 ||
em que P1 e P2 s˜ o pontos de r1 e r2 e V1 e V2 s˜ o vetores diretores de r1 e r2 ,
a a
respectivamente.
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

279. 4.2 ˆ
Angulos e Distˆ ncias
a 267
r2
V2
P2
dist(r1 , r2 )
V1 × V2
V1
r1 P1
Figura 4.30 – Distˆ ncia entre duas retas reversas
a
Marco 2012
¸ Reginaldo J. Santos

280. 268 Retas e Planos
(b) Se os vetores diretores n˜ o s˜ o paralelos, ent˜ o elas s˜ o reversas ou concorren-
a a a a
tes. Os dois casos podem ser resolvidos da mesma forma. Estas retas definem
dois planos paralelos (que podem ser coincidentes, no caso em que elas s˜ o con-
a
correntes). Um e o plano que cont´ m r1 e e paralelo a r2 , vamos cham´ -lo de
´ e ´ a
π1 . O outro, cont´ m r2 e e paralelo a r1 , π2 . O vetor N = V1 × V2 , e normal (ou
e ´ ´
perpendicular) a ambos os planos, em que V1 e V2 s˜ o os vetores diretores de r1
a
e r2 respectivamente. Assim, a distˆ ncia entre as retas e igual a distˆ ncia entre
a ´ ` a
estes dois planos (Figura 4.30), ou seja,
−→ −→
| P1 P2 · N | | P P · (V1 × V2 )|
dist(r1 , r2 ) = dist(π1 , π2 ) = dist(π1 , P2 ) = = 1 2
|| N || ||V1 × V2 ||
(4.12)
em que P1 e P2 s˜ o pontos de r1 e r2 e V1 e V2 s˜ o vetores diretores de r1 e
a a
r2 , respectivamente. Observe que se as retas s˜ o concorrentes a distˆ ncia entre
a a
−→ −→
elas e zero, pois os vetores P1 P2 , V1 e V2 s˜ o coplanares e P1 P2 · (V1 × V2 ) = 0
´ a
(Corol´ rio 3.9 na p´ gina 191).
a a
Exemplo 4.14. Vamos determinar a distˆ ncia entre as retas
a
x−1 y+1 z−2
r1 : = = .
4 −2 −6
e 
 x = 1+2t
r2 : y = −t para todo t ∈ R.
z = 2−3t

As retas s˜ o paralelas, pois seus vetores diretores V1 = (4, −2, −6) e V2 = (2, −1, −3)
a
´ ´
(Exemplo 4.5 na p´ gina 232) s˜ o paralelos (um e um multiplo escalar do outro, ou
a a
ainda as componentes correspondentes s˜ o proporcionais). Al´ m disso, o ponto
a e
P1 = (1, −1, 2) pertence a reta r1 . Como dissemos acima, a distˆ ncia de r1 a r2 e igual
` a ´
a distˆ ncia entre um ponto de r2 e a reta r1 (Figura 4.29). Assim, pela Proposicao 4.5
` a ¸˜
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

281. 4.2 ˆ
Angulos e Distˆ ncias
a 269
na p´ gina 261, temos que
a
−→
|| P1 P2 ×V2 || 13
dist(r1 , r2 ) = dist( P1 , r2 ) = = .
||V2 || 14
As contas s˜ o as mesmas do Exemplo 4.12 na p´ gina 262.
a a
Exemplo 4.15. Determinar a distˆ ncia entre as retas
a
x+1 y−1
r1 : = = z.
3 2
e 
 x = t
r2 : y = 2t para qualquer t ∈ R.
z = 1−t

As retas r1 e r2 s˜ o paralelas aos vetores V1 = (3, 2, 1) e V2 = (1, 2, −1) e passam pelos
a
pontos P1 = (−1, 1, 0) e P2 = (0, 0, 1), respectivamente. As retas n˜ o s˜ o paralelas,
a a
pois seus vetores diretores n˜ o s˜ o paralelos (observe que a 1a componente de V1 e 3
a a . ´
vezes a 1a componente de V2 , mas as 2a ’s componentes s˜ o iguais). Logo,
. . a
−→
P1 P2 = (0 − (−1), 0 − 1, 1 − 0) = (1, −1, 1) .
´
Um vetor perpendicular a ambas as retas e
N = V1 × V2 = (−4, 4, 4) .
Este vetor e normal aos planos π1 (que cont´ m r1 e e paralelo a r2 ) e π2 (que cont´ m
´ e ´ e
r2 e e paralelo a r1 ) (veja a Figura 4.30). Assim,
´
−→
| P1 P2 · N |
dist(r1 , r2 ) = dist(π1 , π2 ) = dist(π1 , P2 ) =
|| N ||
|1(−4) + (−1) · 4 + 1 · 4| | − 4| 1
= = √ = √ .
(−4)2 + 42 + 42 4 3 3
Marco 2012
¸ Reginaldo J. Santos

282. 270 Retas e Planos
Exerc´cios Num´ ricos (respostas na p´ gina 570)
ı e a
4.2.1. Considere os vetores V = i + 3 j + 2k, W = 2i − j + k e U = i − 2 j. Seja π um plano paralelo aos vetores
W e U e r uma reta perpendicular ao plano π. Ache a projecao ortogonal do vetor V sobre a reta r, ou
¸˜
seja, a projecao ortogonal de V sobre o vetor diretor da reta r.
¸˜
4.2.2. Encontrar o angulo entre o plano 2x − y + z = 0 e o plano que passa pelo ponto P = (1, 2, 3) e e perpen-
ˆ ´
dicular ao vetor i − 2 j + k.
4.2.3. Seja π1 o plano que passa pelos pontos A = (1, 1, 1), B = (1, 0, 1), C = (1, 1, 0) e π2 o plano que passa
pelos pontos P = (0, 0, 1) e Q = (0, 0, 0) e e paralelo ao vetor i + j. Ache o angulo entre π1 e π2 .
´ ˆ
4.2.4. Ache uma reta que passa pelo ponto (1, −2, 3) e que forma angulos de 45o e 60o com os eixos x e y
ˆ
respectivamente.
4.2.5. Obtenha os v´ rtices B e C do triˆ ngulo equil´ tero ABC, sendo A = (1, 1, 0) e sabendo que o lado BC est´
e a a a
−→
contido na reta r : ( x, y, z) = t (0, 1, −1). (Sugest˜ o: Determine os pontos Pr da reta r tais que Pr A faz
a
angulo de 60o e 120o com o vetor diretor da reta r)
ˆ
4.2.6. Seja π o plano que passa pela origem e e perpendicular a reta que une os pontos A = (1, 0, 0) e B =
´ `
(0, 1, 0). Encontre a distˆ ncia do ponto C = (1, 0, 1) ao plano π.
a
4.2.7. Seja r1 a reta que passa pelos pontos A = (1, 0, 0) e B = (0, 2, 0), e r2 a reta
y−3 z−4
x−2 = = .
2 3
(a) Encontre as equacoes da reta perpendicular as retas r1 e r2 ;
¸˜ `
(b) Calcule a distˆ ncia entre r1 e r2 .
a
√
4.2.8. Dados A = (0, 2, 1), r : X = (0, 2, −2) + t (1, −1, 2), ache os pontos de r que distam
√ 3 de A. A distˆ ncia
a
do ponto A a reta r e maior, menor ou igual a 3? Por que?
` ´
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

283. 4.2 ˆ
Angulos e Distˆ ncias
a 271
4.2.9. Dada a reta r : X = (1, 0, 0) + t (1, 1, 1) e os pontos A = (1, 1, 1) e B = (0, 0, 1), ache o ponto de r
equidistante de A e B.
4.2.10. Encontre a equacao do lugar geom´ trico dos pontos equidistantes de A = (1, −1, 2) e B = (4, 3, 1). Este
¸˜ e
plano passa pelo ponto m´ dio de AB? Ele e perpendicular ao segmento AB?
e ´
√
4.2.11. Ache as equacoes dos planos em R3 ortogonais ao vetor (2, 2, 2), que distam 3 do ponto (1, 1, 1).
¸˜
¸˜
4.2.12. Obtenha uma equacao geral do plano π, que cont´ m a reta
e
x − 2y + 2z = 0
r :
3x − 5y + 7z = 0
e forma com o plano π1 : x + z = 0 um angulo de 60o .
ˆ
4.2.13. (a) Verifique que a reta r : ( x, y, z) = (1, 0, 1) + t(1, −1, 0) e paralela ao plano
´
π : x + y + z = 0.
(b) Calcule a distˆ ncia de r a π.
a
(c) Existem retas contidas no plano π, que s˜ o reversas a reta r e distam 2 desta?
a `
4.2.14. (a) Determine a equacao do plano π1 que passa por A = (10/3, 1, −1), B = (1, 9/2, −1) e C =
¸˜
(1, −1, 5/6).
(b) Determine a equacao do plano π2 que passa por D = (−1, 4, −1), E = (3/2, −1, 10) e e paralelo ao
¸˜ ´
eixo z.
(c) Escreva equacoes param´ tricas para a reta r intersecao dos planos π1 e π2 .
¸˜ e ¸˜
(d) Faca um esboco dos planos π1 , π2 e da reta r no primeiro octante.
¸ ¸
ˆ
(e) Qual o angulo entre os planos π1 e π2 ?
−→
(f) Qual o ponto P de π1 que est´ mais proximo da origem? (Sugest˜ o: este ponto e tal que OP e
a ´ a ´ ´
ortogonal ao plano π1 .)
Marco 2012
¸ Reginaldo J. Santos

284. 272 Retas e Planos
(g) Qual a area do triˆ ngulo ABC?
´ a
Exerc´cios usando o M ATLAB
ı
4.2.15. Use o M ATLAB para resolver os Exerc´cios Num´ ricos
ı e
Exerc´cios Teoricos
ı ´
4.2.16. Prove que o lugar geom´ trico dos pontos do espaco que equidistam de dois pontos distintos A =
e ¸
( x1 , y1 , z1 ) e B = ( x2 , y2 , z2 ) e um plano que passa pelo ponto m´ dio do segmento AB e e perpendicular
´ e ´
a ele. Esse plano e chamado plano mediador do segmento AB.
´
4.2.17. Mostre que a distˆ ncia de um ponto P0 = ( x0 , y0 , z0 ) a um plano π : ax + by + cz + d = 0 e
a ´
| ax0 + by0 + cz0 + d|
dist( P0 , π ) = √ .
a2 + b2 + c2
4.2.18. Mostre que a distˆ ncia entre dois planos paralelos π1 : ax + by + cz + d1 = 0 e π2 : ax + by + cz + d2 = 0
a
´
e
| d2 − d1 |
dist(π1 , π2 ) = √ .
a2 + b2 + c2
4.2.19. Mostre que a distˆ ncia entre duas retas n˜ o paralelas r1 : ( x, y, z) = ( x1 + ta1 , y1 + tb1 , z1 + tc1 ) e
a a
r2 : ( x, y, z) = ( x2 + ta2 , y2 + tb2 , z2 + tc2 ) e
´
 
x2 − x1 y2 − y1 z2 − z1
det  a1 b1 c1 
a2 b2 c2
2 2 2
b1 c1 a1 c1 a1 b1
det + det + det
b2 c2 a2 c2 a2 b2
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

285. 4.2 ˆ
Angulos e Distˆ ncias
a 273
r
r
π
π
Figura 4.31 – Reta e plano concorrentes Figura 4.32 – Reta e plano paralelos
Marco 2012
¸ Reginaldo J. Santos

286. 274 Retas e Planos
4.2.20. O angulo entre uma reta r que tem vetor diretor V = ( ar , br , cr ) e um plano π que tem vetor normal
ˆ
N = ( aπ , bπ , cπ ) e definido pelo complementar do angulo entre uma reta perpendicular ao plano π e a
´ ˆ
reta r. Mostre que
|N · V|
sen(r, π ) = .
|| N ||||V ||
4.2.21. A distˆ ncia entre uma reta r que passa por um ponto P0 = ( x0 , y0 , z0 ) e tem vetor diretor V = ( ar , br , cr )
a
e um plano π : aπ x + bπ y + cπ z + dπ = 0 e definida como a menor distˆ ncia entre dois pontos um de
´ a
r e outro de π. Se o vetor diretor da reta r, V = ( ar , br , cr ), n˜ o e ortogonal ao vetor normal do plano
a ´
π, N = ( aπ , bπ , cπ ), ent˜ o a reta e o plano s˜ o concorrentes e a distˆ ncia entre eles e igual a zero, caso
a a a ´
contr´ rio a distˆ ncia e igual a distˆ ncia de uma ponto da reta r ao plano π. Mostre que
a a ´ a
 | aπ x0 + bπ y0 + cπ z0 + dπ | , se V · N = 0


a 2 + bπ + c 2
2

dist(r, π ) = π π


0, caso contr´ rio
a

Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

287. 4.3 ¸˜
Posicoes Relativas de Retas e Planos 275
4.3 ¸˜
Posicoes Relativas de Retas e Planos
¸˜
Posicoes Relativas de Duas Retas
−→ −→ −→ −→
Consideremos duas retas quaisquer r1 : OP=OP1 +tV1 e r2 : OP=OP2 +tV2 . Para
¸˜
estudar a posicao relativa destas retas, vamos dividir em dois casos:
(a) Se os vetores diretores s˜ o paralelos, ent˜ o as retas s˜ o paralelas ou coinciden-
a a a
tes (Figura 4.29 na p´ gina 265). Al´ m de paralelas, elas s˜ o coincidentes se, e
a e a
somente se, um ponto de uma reta pertence a outra reta. Portanto, se, e somente
−→
se, P1 P2 e paralelo a V1 (e a V2 , pois V1 e V2 s˜ o paralelos).
´ a
(b) Se os vetores diretores n˜ o s˜ o paralelos, ent˜ o as retas s˜ o reversas ou concor-
a a a a
rentes (Figura 4.30 na p´ gina 267).
a
−→ −→
i. Se os vetores P1 P2 , V1 e V2 s˜ o coplanares, ou seja, se P1 P2 · (V1 × V2 ) = 0
a
(Corol´ rio 3.9 na p´ gina 191), ent˜ o as retas s˜ o concorrentes.
a a a a
−→ −→
ii. Se os vetores P1 P2 , V1 e V2 n˜ o s˜ o coplanares, ou seja, se P1 P2 · (V1 × V2 ) =
a a
0 (Corol´ rio 3.9 na p´ gina 191), ent˜ o as retas s˜ o reversas.
a a a a
¸˜
Posicoes Relativas de Dois Planos
Marco 2012
¸ Reginaldo J. Santos

288. 276 Retas e Planos
π1 π1
π2
π2
Figura 4.33 – Dois planos que se interceptam Figura 4.34 – Dois planos paralelos
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

289. 4.3 ¸˜
Posicoes Relativas de Retas e Planos 277
Sejam dois planos π1 : a1 x + b1 y + c1 z + d1 = 0 e π2 : a2 x + b2 y + c2 z + d2 = 0
quaisquer.
(a) Se os seus vetores normais N1 = ( a1 , b1 , c1 ) e N2 = ( a2 , b2 , c2 ) n˜ o s˜ o parale-
a a
los, ent˜ o os planos s˜ o concorrentes (Figura 4.33).
a a
(b) Se os seus vetores normais s˜ o paralelos, ou seja, se N2 = αN1 , ent˜ o os planos
a a
s˜ o paralelos distintos (Figura 4.34) ou coincidentes. Al´ m de paralelos, eles s˜ o
a e a
¸˜
coincidentes se, e somente se, todo ponto que satisfaz a equacao de π1 , satisfaz
¸˜
tamb´ m a equacao de π2 .
e
Assim
a2 x + b2 y + c2 z + d2 = αa1 x + αb1 y + αc1 z + d2 = α( a1 x + b1 y + c1 z) + d2 =
α(−d1 ) + d2 = 0. Portanto, d2 = αd1 e as equacoes de π1 e π2 s˜ o proporcionais.
¸˜ a
¸˜
Reciprocamente, se as equacoes de π1 e π2 s˜ o proporcionais, ent˜ o claramente
a a
os dois planos s˜ o coincidentes. Portanto, dois planos s˜ o coincidentes se, e
a a
somente se, al´ m dos vetores normais serem paralelos, as suas equacoes s˜ o
e ¸˜ a
proporcionais.
Marco 2012
¸ Reginaldo J. Santos

290. 278 Retas e Planos
r
r
π
π
Figura 4.35 – Reta e plano concorrentes Figura 4.36 – Reta e plano paralelos
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

291. 4.3 ¸˜
Posicoes Relativas de Retas e Planos 279
¸˜
Posicoes Relativas de Reta e Plano
−→ −→
Sejam a reta r : ( x, y, z) =OP=OP0 +tV e o plano π : ax + by + cz + d = 0.
(a) Se o vetor diretor da reta r, V, e o vetor normal do plano π, N = ( a, b, c), s˜ o
a
ortogonais (V · N = 0), ent˜ o a reta e o plano s˜ o paralelos.
a a
Se al´ m dos vetores V e N serem ortogonais, um ponto qualquer da reta per-
e
tence ao plano, por exemplo, se P0 pertence a π (P0 satisfaz a equacao de π),
¸˜
ent˜ o a reta est´ contida no plano.
a a
(b) Se o vetor diretor da reta r, V, e o vetor normal do plano π, N = ( a, b, c), n˜ o
a
s˜ o ortogonais (V · N = 0), ent˜ o a reta e concorrente ao plano.
a a ´
¸˜
Posicoes Relativas de Trˆ s Planos
e
Marco 2012
¸ Reginaldo J. Santos

292. 280 Retas e Planos
π1
π2
π3
Figura 4.37 – Trˆ s planos que se interceptam segundo um ponto
e
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

293. 4.3 ¸˜
Posicoes Relativas de Retas e Planos 281
¸˜
Consideremos trˆ s planos π1 , π2 , e π3 dados pelas equacoes:
e

 π1 : a1 x + b1 y + c1 z = d1
π : a2 x + b2 y + c2 z = d2 (4.13)
 2
π3 : a3 x + b3 y + c3 z = d3
Os vetores Ni = ( ai , bi , ci ) s˜ o normais aos planos πi , para i = 1, 2, 3. Os trˆ s vetores
a e
s˜ o coplanares ou n˜ o s˜ o coplanares.
a a a
(a) Se os vetores N1 , N2 e N3 n˜ o s˜ o coplanares, ent˜ o vamos mostrar que os pla-
a a a
nos se interceptam dois a dois segundo retas que se interceptam em um ponto.
As retas r = π1 ∩ π2 e s = π1 ∩ π3 est˜ o no plano π1 . Vamos mostrar que
a
−→
elas s˜ o concorrentes. Sejam A e B dois pontos distintos da reta r. O vetor AB
a
−→
e perpendicular a N1 e a N2 . Se as retas r e s fossem paralelas, ent˜ o AB se-
´ a
−→
ria perpendicular tamb´ m a N3 , ou seja, AB seria perpendicular a trˆ s vetores
e e
−→
n˜ o coplanares o que implicaria que AB= 0. Os vetores N1 , N2 e N3 n˜ o s˜ o
a a a
coplanares se, e somente se,
det( A) = 0,
 
a1 b1 c1
em que A =  a2 b2 c2 . Neste caso o sistema tem solucao unica (Figura
¸˜ ´
a3 b3 c3
4.37).
(b) Se os trˆ s vetores normais s˜ o coplanares, ent˜ o pode ocorrer uma das seguintes
e a a
¸˜
situacoes:
i. Os vetores normais s˜ o paralelos, ou seja, N1 = αN2 , N1 = βN3 e N2 =
a
γN3 . Neste caso, os planos s˜ o paralelos.
a
e ¸˜
Se al´ m disso, exatamente duas das equacoes s˜ o proporcionais, ent˜ o exa-
a a
a a ¸˜
tamente dois planos s˜ o coincidentes e o sistema n˜ o tem solucao. Se as
¸˜
trˆ s equacoes s˜ o proporcionais, ent˜ o os trˆ s planos s˜ o coincidentes e o
e a a e a
Marco 2012
¸ Reginaldo J. Santos

294. 282 Retas e Planos
π1 π1
π2
π2
π3 π3
Figura 4.38 – Trˆ s planos paralelos
e Figura 4.39 – Planos interceptando-se 2 a 2
π3
π1
π1
π2
π2
π3
Figura 4.40 – Trˆ s planos, sendo 2 paralelos
e ¸˜
Figura 4.41 – Reta intersecao de 3 planos
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

295. 4.3 ¸˜
Posicoes Relativas de Retas e Planos 283
¸˜ ¸˜
sistema tem infinitas solucoes. Se n˜ o ocorre nenhuma destas situacoes, os
a
a a ¸˜
planos s˜ o paralelos e distintos e o sistema n˜ o tem solucao (Figura 4.38).
ii. Exatamente dois vetores normais s˜ o paralelos, ou seja, vale uma, e so-
a
mente uma, equacao entre: N1 = αN2 , N1 = αN3 , N2 = αN3 . Neste caso,
¸˜
exatamente dois planos s˜ o paralelos.
a
Se al´ m de exatamente dois vetores normais serem paralelos, as equacoes
e ¸˜
correspondentes forem proporcionais, ent˜ o dois planos s˜ o coincidentes e
a a
o terceiro corta os dois segundo uma reta. Neste caso o sistema tem infinitas
¸˜
solucoes. Se isto n˜ o acontece, ent˜ o os planos paralelos s˜ o distintos e o
a a a
¸˜
sistema n˜ o tem solucao (Figura 4.40).
a
iii. Os vetores normais s˜ o coplanares e quaisquer dois vetores normais n˜ o
a a
s˜ o paralelos, ou seja, det( A) = 0 e quaisquer dois vetores normais n˜ o
a a
´
s˜ o multiplos escalares. Neste caso, quaisquer dois planos se interceptam
a
¸˜
segundo retas que s˜ o paralelas. Com estas condicoes podem ocorrer dois
a
casos: os trˆ s planos se interceptem segundo uma reta, (Figura 4.41) ou os
e
planos se interceptem, dois a dois, segundo retas distintas (Figura 4.39).
¸˜
No primeiro caso, o sistema (4.13) tem infinitas solucoes. No segundo caso,
o sistema n˜ o tem solucao.
a ¸˜
Marco 2012
¸ Reginaldo J. Santos

296. 284 Retas e Planos
Exerc´cios Num´ ricos (respostas na p´ gina 576)
ı e a
4.3.1. (a) Determine as equacoes da reta r que e a intersecao dos planos:
¸˜ ´ ¸˜
π1 : x − 2y + 2z = 0
π2 : 3x − 5y + 7z = 0.
(b) Qual a posicao relativa da reta r e do plano y + z = 0.
¸˜
4.3.2. Determine a posicao relativa das retas r e s
¸˜
r : ( x, y, z) = (1, 1, 1) + λ(2, 2, 1), ∀ λ ∈ R
s : ( x, y, z) = t(1, 1, 0), ∀ t ∈ R.
4.3.3. Sejam r1 : ( x, y, z) = (1, 0, 2) + (2t, t, 3t) e r2 : ( x, y, z) = (0, 1, −1) + (t, mt, 2mt) duas retas.
(a) Determine m para que as retas sejam coplanares (n˜ o sejam reversas).
a
(b) Para o valor de m encontrado, determine a posicao relativa entre r1 e r2 .
¸˜
(c) Determine a equacao do plano determinado por r1 e r2 .
¸˜
4.3.4. Sejam a reta r : ( x, y, z) = (1, 1, 1) + (2t, mt, t) e o plano π : 2x − y − 2z = 0. Determine o valor de m para
que a reta seja paralela ao plano. Para o valor de m encontrado a reta est´ contida no plano?
a
¸˜
4.3.5. Dˆ a posicao relativa dos seguintes ternos de planos:
e
(a) 2x + y + z = 1, x + 3y + z = 2, x + y + 4z = 3.
(b) x − 2y + z = 0, 2x − 4y + 2z = 1, x + y = 0.
(c) 2x − y + z = 3, 3x − 2y − z = −1, 2x − y + 3z = 7.
(d) 3x + 2y − z = 8, 2x − 5y + 2z = −3, x − y + z = 1.
(e) 2x − y + 3z = −2, 3x + y + 2z = 4, 4x − 2y + 6z = 3.
(f) −4x + 2y − 4z = 6, 3x + y + 2z = 2, 2x − y + 2z = −3.
(g) 6x − 3y + 9z = 3, 4x − 2y + 6z = 5, 2x − y + 3z = 2.
(h) x − 2y + 3z = 2, 3x + y − 2z = 1, 5x − 3y + 4z = 4.
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

297. 4.3 ¸˜
Posicoes Relativas de Retas e Planos 285
Teste do Cap´tulo
ı
1. Ache os pontos do plano π : y = x que equidistam dos pontos A = (1, 1, 0) e B = (0, 1, 1).
2. Quais s˜ o as coordenadas do ponto P , sim´ trico do ponto P = (1, 0, 0) em relacao a reta r : ( x, y, z) =
a e ¸˜ `
t(1, 1, 1)?
3. (a) Encontre a equacao do plano π que passa pelos pontos A = (0, 0, −1), B = (0, 1, 0) e C = (1, 0, 1).
¸˜
(b) Encontre a distˆ ncia da origem ao plano π.
a
4. (a) Mostre que os planos x − y = 0 e y − z = 1 se interceptam segundo uma reta r.
(b) Ache a equacao do plano que passa pelo ponto A = (1, 0, −1) e e perpendicular a reta r.
¸˜ ´ `
Marco 2012
¸ Reginaldo J. Santos

298. 5
¸˜
Secoes Cˆ nicas
o
Uma conica no plano e definida como o conjunto dos pontos P = ( x, y) que satisfa-
ˆ ´
¸˜
zem a equacao
ax2 + bxy + cy2 + dx + ey + f = 0,
em que a, b, c, d, e e f s˜ o numeros reais, com a, b e c n˜ o simultaneamente nulos.
a ´ a
Vamos estudar a elipse, a hip´ rbole e a par´ bola, que s˜ o chamadas conicas n˜ o de-
e a a ˆ a
´
generadas. As outras que incluem um unico ponto e um par de retas s˜ o chamadas
a
ˆ ˆ
conicas degeneradas. Como veremos adiante as conicas n˜ o degeneradas podem
a
¸˜
ser obtidas da intersecao de um cone circular com um plano.
ˆ
Vamos definir as conicas como conjunto de pontos que satisfazem certas proprieda-
¸˜
des e determinar as equacoes na forma mais simples poss´vel.
ı
286

299. 5.1 Cˆ nicas N˜ o Degeneradas
o a 287
5.1 Cˆ nicas N˜ o Degeneradas
o a
5.1.1 Elipse
Marco 2012
¸ Reginaldo J. Santos

300. 288 ¸˜
Secoes Cˆ nicas
o
P
F1 F2
Figura 5.1 – Elipse que e o conjunto dos pontos P tais que dist( P, F1 ) + dist( P, F2 ) = 2a
´
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

301. 5.1 Cˆ nicas N˜ o Degeneradas
o a 289
¸˜
Definicao 5.1. A elipse e o conjunto dos pontos P no plano tais que a soma das distˆ ncias de P a dois pontos
´ a
fixos F1 e F2 (focos) e constante, ou seja, se dist( F1 , F2 ) = 2c, ent˜ o a elipse e o conjunto dos pontos P tais que
´ a ´
dist( P, F1 ) + dist( P, F2 ) = 2a, em que a > c.
Marco 2012
¸ Reginaldo J. Santos

302. 290 ¸˜
Secoes Cˆ nicas
o
A elipse pode ser desenhada se fixarmos as extremidades de um barbante de com-
primento 2a nos focos e esticarmos o barbante com uma caneta. Movimentando-se a
caneta, mantendo o barbante esticado, a elipse ser´ tracada (Figura 5.1).
a ¸
¸˜
Proposicao 5.1. (a) A equa¸ ao da elipse cujos focos s˜ o F1 = (−c, 0) e F2 = (c, 0) e
c˜ a ´
x2 y2
2
+ 2 = 1, (5.1)
a b
(b) A equa¸ ao da elipse cujos focos s˜ o F1 = (0, −c) e F2 = (0, c) e
c˜ a ´
x2 y2
+ 2 = 1. (5.2)
b2 a
√
Em ambos os casos b = a2 − c2 .
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

303. 5.1 Cˆ nicas N˜ o Degeneradas
o a 291
y y
A2
F2
B2
a
c
a
b
A1 A2 B1 B2
F1 c F2 x b x
B1
A1 = (− a, 0) A2 = ( a, 0) A1 = (0, − a) F1 A2 = (0, a)
B1 = (−b, 0) B2 = (b, 0) B1 = (−b, 0) B2 = (b, 0)
F1 = (−c, 0) F2 = (c, 0) F1 = (0, −c) A1 F2 = (0, c)
Figura 5.2 – Elipse com focos nos pontos Figura 5.3 – Elipse com focos nos pontos
F1 = (−c, 0) e F2 = (c, 0) F1 = (0, −c) e F2 = (0, c)
Marco 2012
¸ Reginaldo J. Santos

304. 292 ¸˜
Secoes Cˆ nicas
o
¸˜
Demonstracao. Vamos provar a primeira parte e deixamos para o leitor, como
¸˜ ´
exerc´cio, a demonstracao da segunda parte. A elipse e o conjunto dos pontos
ı
P = ( x, y) tais que
dist( P, F1 ) + dist( P, F2 ) = 2a,
ou seja,
−→ −→
|| F1 P || + || F1 P || = 2a,
´
que neste caso e
( x + c )2 + y2 + ( x − c)2 + y2 = 2a
ou
( x + c)2 + y2 = 2a − ( x − c )2 + y2 .
Elevando ao quadrado e simplificando, temos
a ( x − c)2 + y2 = a2 − cx .
Elevando novamente ao quadrado e simplificando, temos
( a2 − c2 ) x 2 + a2 y2 = a2 ( a2 − c2 )
√
Como a > c, ent˜ o a2 − c2 > 0. Assim, podemos definir b =
a a2 − c2 e dividir e
equacao acima por a2 b2 = a2 ( a2 − c2 ), obtendo (5.1).
¸˜
Nas Figuras 5.2 e 5.3, os pontos A1 e A2 s˜ o chamados v´ rtices da elipse. Os seg-
a e
mentos A1 A2 e B1 B2 s˜ o chamados eixos da elipse.
a
c
A excentricidade da elipse e o numero e = . Como, c < a, a excentricidade de uma
´ ´
a
elipse e um numero real n˜ o negativo menor que 1. Observe que se F1 = F2 , ent˜ o a
´ ´ a a
elipse reduz-se ao c´rculo de raio a. Al´ m disso, como c = 0, ent˜ o e = 0. Assim, um
ı e a
´
c´rculo e uma elipse de excentricidade nula.
ı
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

305. 5.1 Cˆ nicas N˜ o Degeneradas
o a 293
Figura 5.4 – Elipse obtida seccionando-se um cone com um plano
Marco 2012
¸ Reginaldo J. Santos

306. 294 ¸˜
Secoes Cˆ nicas
o
´
A elipse e a curva que se obt´ m seccionando-se um cone com um plano que n˜ o
e a
a ´
passa pelo v´ rtice, n˜ o e paralelo a uma reta geratriz (reta que gira em torno do
e
eixo do cone de forma a ger´ -lo) e que corta apenas uma das folhas da superf´cie (a
a ı
¸˜
demonstracao deste fato est´ no Exerc´cio 7.3.11 na p´ gina 505).
a ı a
¸˜
A elipse tem a propriedade de refletir os raios vindos de um dos focos na direcao do
¸˜
outro foco (a demonstracao deste fato est´ no Exerc´cio 5.2.12 na p´ gina 351). Este
a ı a
´ ¸˜
fato e usado na construcao de espelhos para dentistas e para escaneres.
´
Os planetas possuem orbitas el´pticas em torno do Sol, assim como os sat´ lites em
ı e
´ ´
torno dos planetas. A excentricidade da orbita da Terra em torno do Sol e 0,017. Da
´ ´ ´
Lua em volta da Terra e 0,055. Netuno e o planeta, cuja orbita, tem a menor excentri-
´ ´ ´ ´
cidade do sistema solar, que e 0,005. Mercurio tem a orbita de maior, e e 0,206. Triton,
´ ´ ´
que e a maior lua de Netuno e o corpo, cuja orbita tem a menor excentricidade do
´ ´
sistema solar, que e de 0,00002. O cometa Halley tem uma orbita el´ptica em torno do
ı
sol com excentricidade 0,967. O coliseu de Roma tem a base el´ptica com eixo maior
ı
igual a 94 metros e eixo menor igual a 78 metros.
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

307. 5.1 Cˆ nicas N˜ o Degeneradas
o a 295
5.1.2 Hip´ rbole
e
Marco 2012
¸ Reginaldo J. Santos

308. 296 ¸˜
Secoes Cˆ nicas
o
P
F1 F2
Figura 5.5 – Hip´ rbole que e o conjunto dos pontos P = ( x, y) tais que | dist( P, F1 ) − dist( P, F2 )| = 2a
e ´
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

309. 5.1 Cˆ nicas N˜ o Degeneradas
o a 297
¸˜
Definicao 5.2. A hip´ rbole e o conjunto dos pontos P no plano tais que o modulo da diferenca entre as
e ´ ´ ¸
distˆ ncias de P a dois pontos fixos F1 e F2 (focos) e constante, ou seja, se dist( F1 , F2 ) = 2c, ent˜ o a hip´ rbole e
a ´ a e ´
o conjunto dos pontos P tais que
| dist( P, F1 ) − dist( P, F2 )| = 2a,
em que a < c.
Podemos desenhar uma parte de um ramo da hip´ rbole da seguinte forma. Fixamos
e
uma extremidade de uma r´ gua em um dos focos, fixamos uma extremidade de um
e
barbante (de comprimento igual ao comprimento da r´ gua menos 2a) na outra ponta
e
da r´ gua e a outra extremidade do barbante no outro foco. Esticamos o barbante com
e
uma caneta de forma que ela fique encostada na r´ gua. Girando-se a r´ gua em torno
e e
do foco no qual ela foi fixada, mantendo o barbante esticado com a caneta encostada
na r´ gua, uma parte de um ramo da hip´ rbole ser´ tracada (Figura 5.5).
e e a ¸
Marco 2012
¸ Reginaldo J. Santos

310. 298 ¸˜
Secoes Cˆ nicas
o
y y
y=−bx
a y= bx
a
y=−ax F2 y= ax
b b
A2
b
c
a
b c
A1 A2
a
F1 F2 x x
A1
F1
A1 = (− a, 0) A2 = ( a, 0) A1 = (0, − a) A2 = (0, a)
F1 = (0, −c) F2 = (0, c)
F1 = (−c, 0) F2 = (c, 0)
Figura 5.6 – Hip´ rbole com focos nos pontos
e Figura 5.7 – Hip´ rbole com focos nos pontos
e
F1 = (−c, 0) e F2 = (c, 0) F1 = (0, −c) e F2 = (0, c)
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

311. 5.1 Cˆ nicas N˜ o Degeneradas
o a 299
¸˜
Proposicao 5.2. (a) A equa¸ ao da hip´ rbole cujos focos s˜ o F1 = (−c, 0) e F2 = (c, 0) e
c˜ e a ´
x2 y2
2
− 2 =1 (5.3)
a b
e das ass´ntotas (retas para onde a curva se aproxima, quando x → ±∞) s˜ o
ı a
b
y = ± x,
a
(b) A equa¸ ao da hip´ rbole cujos focos s˜ o F1 = (0, −c) e F2 = (0, c) e
c˜ e a ´
y2 x2
2
− 2 =1 (5.4)
a b
e das ass´ntotas s˜ o
ı a
a
x = ± y.
b
√
Em ambos os casos b = c2 − a2 .
¸˜
Demonstracao. Vamos provar a primeira parte e deixamos para o leitor, como
¸˜ ´
exerc´cio, a demonstracao da segunda parte. A hip´ rbole e o conjunto dos pontos
ı e
P = ( x, y) tais que
dist( P, F1 ) − dist( P, F2 ) = ±2a,
ou seja,
−→ −→
|| F1 P || − || F2 P || = ±2a,
´
que neste caso e
( x + c )2 + y2 − ( x − c)2 + y2 = ±2a
Marco 2012
¸ Reginaldo J. Santos

312. 300 ¸˜
Secoes Cˆ nicas
o
ou
( x + c)2 + y2 = ±2a + ( x − c )2 + y2 .
Elevando ao quadrado e simplificando, temos
±a ( x − c)2 + y2 = a2 − cx .
Elevando novamente ao quadrado e simplificando, temos
( a2 − c2 ) x 2 + a2 y2 = a2 ( a2 − c2 )
√
Como a < c, ent˜ o c2 − a2 > 0. Assim, podemos definir b = c2 − a2 e dividir e
a
equacao acima por − a2 b2 = a2 ( a2 − c2 ), obtendo (5.3).
¸˜ √
Se a equacao (5.3) e resolvida em y obtemos y = ± b x2 − a2 que, para x > 0, pode
¸˜ ´ a
ser escrita como
b a2
y = ± x 1− 2.
a x
Para x > 0 muito grande, o radical no segundo membro e proximo de 1 e a equacao
´ ´ ¸˜
se aproxima de
b
y = ± x.
a
O mesmo ocorre para x < 0 muito grande em modulo (verifique!).
´
Nas Figuras 5.6 e 5.7, os pontos A1 e A2 s˜ o chamados v´ rtices da hip´ rbole. A
a e e
c
excentricidade da hip´ rbole e o numero e = . Como, c > a, a excentricidade de
e ´ ´
a
´ ´
uma hip´ rbole e um numero real maior que 1.
e
e ´
A hip´ rbole e a curva que se obt´ m seccionando-se um cone com um plano que n˜ o
e a
a ´
passa pelo v´ rtice, n˜ o e paralelo a uma reta geratriz e que corta as duas folhas da
e
¸˜
superf´cie (a demonstracao deste fato est´ no Exerc´cio 7.3.11 na p´ gina 505).
ı a ı a
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

313. 5.1 Cˆ nicas N˜ o Degeneradas
o a 301
¸˜
A hip´ rbole tem a propriedade de refletir os raios vindos na direcao de um dos focos
e
¸˜ ¸˜
na direcao do outro foco (a demonstracao deste fato est´ no Exerc´cio 5.2.13 na p´ gina
a ı a
´ ¸˜ ´
355). Este fato e usado na construcao de espelhos para telescopios e para m´ quinas
a
fotogr´ ficas.
a
O cometa C/1980 E1 foi descoberto em 1980 e est´ deixando o sistema solar numa
a
´ ´
trajetoria hiperbolica com a maior velocidade j´ observada em um corpo no sistema
a
solar.
Marco 2012
¸ Reginaldo J. Santos

314. 302 ¸˜
Secoes Cˆ nicas
o
Figura 5.8 – Hip´ rbole obtida seccionando-se um cone com um plano
e
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

315. 5.1 Cˆ nicas N˜ o Degeneradas
o a 303
5.1.3 Par´ bola
a
Marco 2012
¸ Reginaldo J. Santos

316. 304 ¸˜
Secoes Cˆ nicas
o
P
F
Figura 5.9 – Par´ bola que e o conjunto dos pontos P = ( x, y) tais que dist( P, F ) = dist( P, r )
a ´
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

317. 5.1 Cˆ nicas N˜ o Degeneradas
o a 305
¸˜
Definicao 5.3. Uma par´ bola e o conjunto dos pontos P no plano equidistantes de uma reta r (diretriz) e de
a ´
um ponto F (foco), n˜ o pertencente a r, ou seja, a par´ bola e o conjunto dos pontos P tais que
a a ´
dist( P, F ) = dist( P, r ).
Podemos desenhar uma parte de uma par´ bola da seguinte forma. Colocamos um
a
esquadro com um lado cateto encostado na reta diretriz, fixamos uma extremidade
de um barbante (de comprimento igual ao lado cateto do esquadro perpendicular a `
reta diretriz) no foco, a outra extremidade na ponta do esquadro oposta ao lado que
est´ encostado na reta diretriz. Esticamos o barbante com a caneta de forma que ela
a
`
fique encostada no lado do esquadro perpendicular a reta diretriz. Deslizando-se o
¸˜
esquadro na direcao da reta diretriz mantendo o lado encostado nela uma parte da
a ´
par´ bola e tracada (Figura 5.9).
¸
Marco 2012
¸ Reginaldo J. Santos

318. 306 ¸˜
Secoes Cˆ nicas
o
y y
r : x = −p
P0 F
x
F = (0, p)
P0 = (0, 0) x
r : y = −p
F = ( p, 0)
P0 = (0, 0)
Figura 5.10 – Par´ bola com foco no ponto F = ( p, 0) e
a Figura 5.11 – Par´ bola com foco no ponto F = (0, p) e
a
p>0 p>0
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

319. 5.1 Cˆ nicas N˜ o Degeneradas
o a 307
y y
r : y = −p
r : x = −p
P0
x
F
F P0
x
F = ( p, 0) F = (0, p)
P0 = (0, 0) P0 = (0, 0)
Figura 5.12 – Par´ bola com foco no ponto F = ( p, 0) e
a Figura 5.13 – Par´ bola com foco no ponto F = (0, p) e
a
p<0 p<0
Marco 2012
¸ Reginaldo J. Santos

320. 308 ¸˜
Secoes Cˆ nicas
o
¸˜
Proposicao 5.3. (a) A equa¸ ao da parabola com foco F = ( p, 0) e reta diretriz r : x = − p e
c˜ ´ ´
y2 = 4px . (5.5)
(b) A equa¸ ao de uma parabola com foco F = (0, p) e reta diretriz r : y = − p e
c˜ ´ ´
x2 = 4py . (5.6)
¸˜
Demonstracao. Vamos provar a primeira parte e deixamos para o leitor, como
¸˜ ´
exerc´cio, a demonstracao da segunda parte. A par´ bola e o conjunto dos pontos
ı a
P = ( x, y) tais que
dist( P, F ) = dist( P, r ) ,
´
que neste caso e
( x − p )2 + y2 = | x + p | ,
Elevando ao quadrado e simplificando, obtemos (5.5).
Nas Figuras 5.10, 5.11, 5.12 e 5.13, o ponto P0 e o ponto da par´ bola mais proximo
´ a ´
´ e a a ´
da reta diretriz e e chamado de v´ rtice da par´ bola. A par´ bola e a curva que se
obt´ m seccionando-se um cone por um plano paralelo a uma reta geratriz do cone
e
¸˜
conforme a Figura 5.14 (a demonstracao deste fato est´ no Exerc´cio 7.3.11 na p´ gina
a ı a
505).
¸˜
A par´ bola tem a propriedade de refletir os raios vindos do foco na direcao do seu
a
¸˜
eixo (a demonstracao deste fato est´ no Exerc´cio 5.2.12 na p´ gina 316). Este fato e
a ı a ´
¸˜ ´ ¸˜
usado na construcao de farois e lanternas. Tamb´ m, naturalmente, reflete na direcao
e
¸˜
do foco os raios que incidem paralelos ao eixo de simetria, fato usado na construcao
de antenas receptoras.
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

321. 5.1 Cˆ nicas N˜ o Degeneradas
o a 309
Figura 5.14 – Par´ bola obtida seccionando-se um cone com um plano
a
Marco 2012
¸ Reginaldo J. Santos

322. 310 ¸˜
Secoes Cˆ nicas
o
¸˜
5.1.4 Caracterizacao das Cˆ nicas
o
ˆ ¸˜
Vamos mostrar a seguir que todas as conicas n˜ o degeneradas, com excecao da cir-
a
cunferˆ ncia, podem ser descritas de uma mesma maneira.
e
¸˜
Proposicao 5.4. Seja s uma reta fixa (diretriz) e F um ponto fixo (foco) n˜ o pertencente a s. O conjunto dos pontos do
a
plano P = ( x, y) tais que
dist( P, F ) = e dist( P, s), (5.7)
em que e > 0 e uma constante fixa, e uma cˆ nica.
´ ´ o
(a) Se e = 1, ent˜ o a cˆ nica e uma par´ bola.
a o ´ a
(b) Se 0 < e < 1, ent˜ o a cˆ nica e uma elipse.
a o ´
(c) Se e > 1, ent˜ o a cˆ nica e uma hip´rbole.
a o ´ e
Reciprocamente, toda cˆ nica que n˜ o seja uma circunferˆncia pode ser descrita por uma equa¸ ao da forma (5.7).
o a e c˜
¸˜
Demonstracao. Se e = 1, a equacao (5.7) e a propria definicao da par´ bola. Vamos
¸˜ ´ ´ ¸˜ a
considerar o caso em que e > 0, com e = 1. Seja d = dist( F, s). Sem perda de
generalidade podemos tomar o foco como sendo o ponto F = ( p, 0) e a diretriz
p 2
como sendo a reta vertical s : x = 2 , em que p = 1dee2 se a reta s estiver a direita do
−
`
e
de 2
foco F (Figuras 5.15 e 5.16) e p = e2 −1 se a reta s estiver a esquerda do foco F (Figuras
`
5.17 e 5.18).
Assim o conjunto dos pontos P = ( x, y) tais que
dist( P, F ) = e dist( P, s) ,
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

323. 5.1 Cˆ nicas N˜ o Degeneradas
o a 311
pode ser descrito como sendo o conjunto dos pontos P = ( x, y) tais que
p
( x − p )2 + y2 = e x − ,
e2
Elevando ao quadrado e simplificando, obtemos
1
(1 − e2 ) x 2 + y2 = p2 −1
e2
que pode ainda ser escrito como
x2 y2
p2
+ p2 (1− e2 )
= 1. (5.8)
e2 e2
Se 0 < e < 1, esta e a equacao de uma elipse. Se e > 1, e a equacao de uma hip´ rbole.
´ ¸˜ ´ ¸˜ e
Para mostrar a rec´proca, considere uma elipse ou hip´ rbole com excentricidade e >
ı e
´ a
0 e um dos focos em F = ( p, 0). E f´ cil verificar que (5.8) e a equacao desta conica e
´ ¸˜ ˆ
p
portanto (5.7) tamb´ m o e, com a reta diretriz sendo s : x = 2 .
e ´
e
Marco 2012
¸ Reginaldo J. Santos

324. 312 ¸˜
Secoes Cˆ nicas
o
y y
s:x= 2
p
e
s:x= 2
p
e
F F
( p, 0) x ( p, 0) x
Figura 5.15 – Elipse, um de seus focos e a reta diretriz Figura 5.16 – Hip´ rbole, um de seus focos e a reta di-
e
`
a direita `
retriz a direita
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

325. 5.1 Cˆ nicas N˜ o Degeneradas
o a 313
y y
s:x= 2
s:x= 2
p
p
e
e
F F
( p, 0) x ( p, 0) x
Figura 5.17 – Elipse, um de seus focos e a reta diretriz Figura 5.18 – Hip´ rbole, um de seus focos e a reta di-
e
`
a esquerda `
retriz a esquerda
Marco 2012
¸ Reginaldo J. Santos

326. 314 ¸˜
Secoes Cˆ nicas
o
Exerc´cios Num´ ricos (respostas na p´ gina 580)
ı e a
¸˜ ˆ
5.1.1. Reduzir cada uma das equacoes de forma a identificar a conica que ela representa e faca um esboco do
¸ ¸
seu gr´ fico:
a
(a) 4x2 + 2y2 = 1
(c) x2 − 9y2 = 9
(b) x2 + y = 0
¸˜
5.1.2. Escreva as equacoes das seguintes elipses:
(a) Os focos s˜ o F1 = (−1, 2) e F2 = (3, 2) e satisfaz dist( P, F1 ) + dist( P, F2 ) = 6;
a
(b) Os focos s˜ o F1 = (−1, −1) e F2 = (1, 1) e satisfaz dist( P, F1 ) + dist( P, F2 ) = 4;
a
¸˜
5.1.3. Escreva as equacoes das seguintes hip´ rboles:
e
(a) Os focos s˜ o F1 = (3, −1) e F2 = (3, 4) e satisfaz | dist( P, F1 ) − dist( P, F2 )| = 3;
a
(b) Os focos s˜ o F1 = (−1, −1) e F2 = (1, 1) e satisfaz | dist( P, F1 ) − dist( P, F2 )| = 2;
a
¸˜
5.1.4. Escreva as equacoes das seguintes par´ bolas:
a
(a) O foco e F = (0, 2) e diretriz y = −2;
´
(b) O foco e F = (0, 0) e diretriz x + y = 2;
´
¸˜ ´
5.1.5. Determinar a equacao e identificar a trajetoria de um ponto que se move de maneira que sua distˆ ncia
a
ao ponto F = (6, 0) e sempre igual a duas vezes sua distˆ ncia a reta 2x − 3 = 0.
´ a
¸˜ ´
5.1.6. Determinar a equacao e identificar a trajetoria de um ponto que se move de maneira que sua distˆ ncia
a
ao eixo y e sempre igual a duas vezes sua distˆ ncia ao ponto F = (3, 2).
´ a
Exerc´cios Teoricos
ı ´
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

327. 5.1 Cˆ nicas N˜ o Degeneradas
o a 315
5.1.7. Mostre que a equacao da elipse com focos nos pontos F1 = ( x0 − c, y0 ) e F2 = ( x0 + c, y0 ) e satisfaz
¸˜
dist( P, F1 ) + dist( P, F2 ) = 2a, em que a > c
´
e
( x − x0 )2 ( y − y0 )2
+ = 1,
a2 b2
√
em que b = a2 − c2 .
5.1.8. Mostre que a equacao da hip´ rbole com focos nos pontos F1 = ( x0 − c, y0 ) e F2 = ( x0 + c, y0 ) e satisfaz
¸˜ e
| dist( P, F1 ) − dist( P, F2 )| = 2a, em que a < c
´
e
( x − x0 )2 ( y − y0 )2
− = 1,
a2 b2
√
em que b = c2 − a2 .
5.1.9. Mostre que a equacao da par´ bola com foco no ponto F = ( x0 + p, y0 ) e reta diretriz r : x = x0 − p e
¸˜ a ´
(y − y0 )2 = 4p( x − x0 ).
5.1.10. Seja uma elipse ou hip´ rbole com focos em F1 = ( p, 0) e F2 = (− p, 0).
e
(a) Mostre que
x2 y2
p2
+ p2 (1− e2 )
=1
e2 e2
e a equacao desta conica, em que e e a excentricidade.
´ ¸˜ ˆ ´
p
(b) Definindo a reta r : x = 2 , Mostre que esta conica pode ser descrita pelo conjunto de pontos
ˆ
e
P = ( x, y) tais que
dist( P, F ) = e dist( P, r ).
Marco 2012
¸ Reginaldo J. Santos

328. 316 ¸˜
Secoes Cˆ nicas
o
5.1.11. (a) Verifique que com o procedimento abaixo realmente desenhamos uma parte de um ramo de uma
hip´ rbole. Fixamos uma extremidade de uma r´ gua em um dos focos, fixamos uma extremidade de
e e
um barbante (de comprimento igual ao comprimento da r´ gua menos 2a) na outra ponta da r´ gua e
e e
a outra extremidade do barbante no outro foco. Esticamos o barbante com uma caneta de forma que
ela fique encostada na r´ gua. Girando-se a r´ gua em torno do foco no qual ela foi fixada, mantendo
e e
o barbante esticado com a caneta encostada na r´ gua, uma parte de um ramo da hip´ rbole ser´
e e a
tracada (Figura 5.5 na p´ gina 296).
¸ a
(b) Verifique que com o procedimento abaixo realmente desenhamos uma parte de um ramo de uma
par´ bola. Colocamos um esquadro com um lado cateto encostado na reta diretriz, fixamos uma ex-
a
`
tremidade de um barbante (de comprimento igual ao lado cateto do esquadro perpendicular a reta
diretriz) no foco, a outra extremidade na ponta do esquadro oposta ao lado que est´ encostado na
a
reta diretriz. Esticamos o barbante com a caneta de forma que ela fique encostada no lado do esqua-
` ¸˜
dro perpendicular a reta diretriz. Deslizando-se o esquadro na direcao da reta diretriz mantendo o
a ´
lado encostado nela uma parte da par´ bola e tracada (Figura 5.9 na p´ gina 304).
¸ a
´ ¸˜
5.1.12. Mostre que um espelho parabolico reflete na direcao do foco os raios que incidem paralelos ao seu eixo
de simetria seguindo os seguintes passos:
(a) Considere a par´ bola y2 = 4px. Usando o fato de que a inclinacao da reta tangente a parabola no
a ¸˜ `
0 y2 dy 2p
ponto P = ( 4p , y0 ) e tan(α) =
´ dx = y0 . Mostre que se o raio incidente tem equacao y = y0 , ent˜ o a
¸˜ a
0 y2
equacao do raio refletido que passa por P = ( 4p , y0 ) e
¸˜ ´
4py0 y2
y − y0 = ( x − 0 ).
y2 − 4p2
0
4p
2 tan α
Use o fato de que tan(2α) = 1−tan2 α
.
(b) Mostre que o raio refletido intercepta o eixo x em x = p.
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

329. 5.1 Cˆ nicas N˜ o Degeneradas
o a 317
a ¸˜
Figura 5.19 – Par´ bola refletindo na direcao do foco ¸˜
Figura 5.20 – Par´ bola refletindo na direcao do seu
a
os raios paralelos ao seu eixo de simetria. eixo de simetria os raios origin´ rios do foco.
a
Marco 2012
¸ Reginaldo J. Santos

330. 318 ¸˜
Secoes Cˆ nicas
o
y
P α
α
2α
α
x
¸˜
Figura 5.21 – Par´ bola refletindo na direcao do foco os raios paralelos ao seu eixo de simetria.
a
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

331. 5.2 ¸˜
Coordenadas Polares e Equacoes Param´ tricas
e 319
5.2 ¸˜
Coordenadas Polares e Equacoes Param´ tricas
e
At´ agora vimos usando o chamado sistema de coordenadas cartesianas, em que
e
´ ¸˜
um ponto do plano e localizado em relacao a duas retas fixas perpendiculares entre
si. Vamos definir um outro sistema de coordenadas chamado de sistema de coorde-
´ ¸˜
nadas polares em que um ponto do plano e localizado em relacao a um ponto e a
uma reta que passa por esse ponto.
Escolhemos um ponto O (usualmente a origem do sistema cartesiano), chamado
polo e uma reta orientada passando pelo polo chamada eixo polar (usualmente to-
´
mamos o proprio eixo x do sistema cartesiano). No sistema de coordenadas polares
um ponto no plano e localizado dando-se a distˆ ncia do ponto ao polo, r = dist( P, O)
´ a
−→
e o angulo, θ, entre os vetores OP e um vetor na direcao e sentido do eixo polar, com
ˆ ¸˜
¸˜ ´
a mesma convencao da trigonometria, ou seja, ele e positivo se medido no sentido
anti-hor´ rio a partir do eixo polar e negativo se medido no sentido hor´ rio a partir
a a
do eixo polar. As coordenadas polares de um ponto P do plano s˜ o escritas na forma
a
(r, θ ).
¸˜
Segue facilmente as relacoes entre as coordenadas cartesianas e as coordenadas po-
lares.
¸˜
Proposicao 5.5. Suponha que o polo e o eixo polar do sistema de coordenadas polares coincidem com a origem e o eixo x
do sistema de coordenadas cartesianas, respectivamente. Ent˜ o a transforma¸ ao entre os sistemas de coordenadas polares
a c˜
e o de coordenadas cartesianas podem ser realizadas pelas equa¸ oes
c˜
x = r cos θ e y = r sen θ
r= x 2 + y2 ,
x y
cos θ = e sen θ = , se x2 + y2 = 0.
x 2 + y2 x 2 + y2
Marco 2012
¸ Reginaldo J. Santos

332. 320 ¸˜
Secoes Cˆ nicas
o
y
P
y
r
θ
O x x
Figura 5.22 – Ponto P do plano em coordenadas polares (r, θ ) e cartesianas ( x, y)
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

333. 5.2 ¸˜
Coordenadas Polares e Equacoes Param´ tricas
e 321
y
(|r |, θ )
θ+π θ
x
(r, θ ) = (|r |, θ + π )
Figura 5.23 – Para r < 0, (r, θ ) = (|r |, θ + π )
Marco 2012
¸ Reginaldo J. Santos

334. 322 ¸˜
Secoes Cˆ nicas
o
Estendemos as coordenadas polares para o caso no qual r e negativo da seguinte
´
forma:
para r < 0, (r, θ ) = (|r |, θ + π ).
Assim, (r, θ ) e (−r, θ ) est˜ o na mesma reta que passa pelo polo, a distˆ ncia |r | do
a ` a
¸˜
polo, mas em lados opostos em relacao ao polo.
Exemplo 5.1. Vamos determinar a equacao em coordenadas polares da circun-
¸˜
¸˜ ´
ferˆ ncia cuja equacao em coordenadas retangulares e
e
( x − 1)2 + ( y − 1)2 = 2
ou simplificando
x2 + y2 − 2x − 2y = 0.
Substituindo-se x por r cos θ e y por r sen θ obtemos
r2 − 2r cos θ − 2r sen θ = 0.
Dividindo-se por r ficamos com
r − 2 cos θ − 2 sen θ = 0.
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

335. 5.2 ¸˜
Coordenadas Polares e Equacoes Param´ tricas
e 323
2.5
y
2
1.5
1
0.5
0
x
−0.5
−0.5 0 0.5 1 1.5 2 2.5
Figura 5.24 – Circunferˆ ncia com equacao em coordenadas polares r − 2 cos θ − 2 sen θ = 0
e ¸˜
Marco 2012
¸ Reginaldo J. Santos

336. 324 ¸˜
Secoes Cˆ nicas
o
y
1
0.8
0.6
0.4
0.2
0
x
−0.2
−0.4
−0.6
−0.8
−1
−1 −0.5 0 0.5
1
Figura 5.25 – Par´ bola com equacao em coordenadas polares r =
a ¸˜
1 − cos θ
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

337. 5.2 ¸˜
Coordenadas Polares e Equacoes Param´ tricas
e 325
Exemplo 5.2. Vamos determinar a equacao em coordenadas retangulares do lugar
¸˜
¸˜ ´
geom´ trico cuja equacao em coordenadas polares e
e
1
r= .
1 − cos θ
x
Substituindo-se r por x2 + y2 e cos θ por obtemos
x2 + y2
1
x 2 + y2 = x
1− √
x 2 + y2
ou simplificando
x2 + y2 − x = 1.
Somando-se x a ambos os membros obtemos
x2 + y2 = 1 + x.
Elevando-se ao quadrado obtemos
x 2 + y2 = (1 + x )2 .
Simplificando-se obtemos ainda
y2 = 1 + 2x = 2( x + 1/2),
que e uma par´ bola com foco na origem F = (0, 0) e reta diretriz x = −1 (verifique!).
´ a
5.2.1 Cˆ nicas em Coordenadas Polares
o
¸˜ ˆ a ´
A equacao polar de uma conica, que n˜ o e uma circunferˆ ncia, assume uma forma
e
simples quando um foco F est´ no polo e a reta diretriz s e paralela ou perpendicular
a ´
Marco 2012
¸ Reginaldo J. Santos

338. 326 ¸˜
Secoes Cˆ nicas
o
ao eixo polar. Seja d = dist( F, s). Para deduzir a equacao polar das conicas vamos
¸˜ ˆ
¸˜ ¸˜ ˆ
usar a caracterizacao dada na Proposicao 5.4 na p´ gina 310, ou seja, que uma conica
a
e o lugar geom´ trico dos pontos P que satisfazem
´ e
dist( P, F ) = e dist( P, s)
Como o foco F est´ no polo, temos que dist( P, F ) = r, em que (r, θ ) s˜ o as coordena-
a a
das polares de P.
(a) Se a reta diretriz, s, e perpendicular ao eixo polar.
´
(i) Se a reta s est´ a direita do polo, obtemos que dist( P, s) = d − r cos θ. Assim
a`
¸˜ ˆ
a equacao da conica fica sendo
r = e(d − r cos θ ).
Isolando r obtemos
de
r= .
1 + e cos θ
(ii) Se a reta s est´ a esquerda do polo, obtemos que dist( P, s) = d + r cos θ.
a `
¸˜ ˆ
Assim a equacao da conica fica sendo
r = e(d + r cos θ ).
Isolando r obtemos
de
r= .
1 − e cos θ
(b) Se a reta diretriz, s, e paralela ao eixo polar.
´
(i) Se a reta s est´ acima do polo, obtemos que dist( P, s) = d − r sen θ. Assim a
a
¸˜ ˆ
equacao da conica fica sendo
r = e(d − r sen θ ).
Isolando r obtemos
de
r= .
1 + e sen θ
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

339. 5.2 ¸˜
Coordenadas Polares e Equacoes Param´ tricas
e 327
(ii) Se a reta s est´ abaixo do polo, obtemos que dist( P, s) = d + r sen θ. Assim
a
¸˜ ˆ
a equacao da conica fica sendo
r = e(d + r sen θ ).
Isolando r obtemos
de
r= .
1 − e sen θ
Isto prova o seguinte resultado
¸˜
Proposicao 5.6. Considere uma cˆ nica com excentricidade e > 0 (que n˜ o e uma circunferˆncia), que tem um foco F no
o a ´ e
polo e a reta diretriz s e paralela ou perpendicular ou eixo polar, com d = dist(s, F ).
´
´ a`
(a) Se a reta diretriz correspondente a F e perpendicular ao eixo polar e est´ a direita do polo, ent˜ o a equa¸ ao polar da
a c˜
cˆ nica e
o ´
de
r=
1 + e cos θ
a`
e se est´ a esquerda do polo, ent˜ o a equa¸ ao polar da cˆ nica e
a c˜ o ´
de
r=
1 − e cos θ
(b) Se a reta diretriz correspondente a F e paralela ao eixo polar e est´ acima do polo, ent˜ o a equa¸ ao polar da cˆ nica e
´ a a c˜ o ´
de
r=
1 + e sen θ
e se est´ abaixo do polo, ent˜ o a equa¸ ao polar da cˆ nica e
a a c˜ o ´
de
r=
1 − e sen θ
Marco 2012
¸ Reginaldo J. Santos

340. 328 ¸˜
Secoes Cˆ nicas
o
y y
s s P
P
−r
=
|r |
r
θ
θ
x x
ˆ
Figura 5.26 – Parte de uma conica com foco no polo e Figura 5.27 – Hip´ rbole com foco no polo e reta dire-
e
`
reta diretriz perpendicular ao eixo polar a direita `
triz perpendicular ao eixo polar a direita
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

341. 5.2 ¸˜
Coordenadas Polares e Equacoes Param´ tricas
e 329
y y
s s
P
r
θ
θ
x x
−r
=
|r |
P
ˆ
Figura 5.28 – Parte de uma conica com foco no polo e Figura 5.29 – Hip´ rbole com foco no polo e reta dire-
e
`
reta diretriz perpendicular ao eixo polar a esquerda `
triz perpendicular ao eixo polar a esquerda
Marco 2012
¸ Reginaldo J. Santos

342. 330 ¸˜
Secoes Cˆ nicas
o
y y
P
s
−r
=
|r |
P
r
θ
x s
θ
x
ˆ
Figura 5.30 – Parte de uma conica com foco no polo e Figura 5.31 – Hip´ rbole com foco no polo e reta dire-
e
reta diretriz paralela ao eixo polar acima triz paralela ao eixo polar acima
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

343. 5.2 ¸˜
Coordenadas Polares e Equacoes Param´ tricas
e 331
y y
θ
x
s
θ
−r
x
=
r
|r |
P
P
s
ˆ
Figura 5.32 – Parte de uma conica com foco no polo e Figura 5.33 – Hip´ rbole com foco no polo e reta dire-
e
reta diretriz paralela ao eixo polar abaixo triz paralela ao eixo polar abaixo
Marco 2012
¸ Reginaldo J. Santos

344. 332 ¸˜
Secoes Cˆ nicas
o
Exemplo 5.3. Vamos identificar a conica cuja equacao em coordenadas polares e
ˆ ¸˜ ´
4
r= .
2 + cos θ
¸˜
Dividindo-se o numerador e o denominador do segundo membro da equacao por 2
obtemos
2
r= 1
,
1 + 2 cos θ
´ ¸˜
que e a equacao em coordenadas polares de uma elipse com excentricidade igual
a 1/2, um dos focos no polo, reta diretriz x = 4 (coordenadas cartesianas) ou
r cos θ = 4 (coordenadas polares). Fazendo θ = 0 e θ = π na equacao polar da
¸˜
elipse encontramos r = 4/3 e r = 2, respectivamente. (4/3, 0) e (2, π ) s˜ o coordena-
a
das polares de v´ rtices da elipse.
e
5.2.2 Circunferˆ ncia em Coordenadas Polares
e
¸˜
A forma mais simples da equacao de uma circunferˆ ncia em coordenadas polares
e
ocorre quando seu centro est´ no polo. Neste caso a equacao e simplesmente r =
a ¸˜ ´
a, em que a e o raio da circunferˆ ncia. Al´ m deste caso, a equacao polar de uma
´ e e ¸˜
circunferˆ ncia assume uma forma simples quando ela passa pelo polo e o seu centro
e
est´ no eixo polar ou na reta perpendicular ao eixo polar que passa pelo polo.
a
(a) Se o centro est´ no eixo polar.
a
(a) Se o raio e igual a a e o centro em coordenadas polares e C = ( a, 0). Se P e
´ ´ ´
um ponto qualquer da circunferˆ ncia, ent˜ o
e a
−→ −→ −→ −→ −→ −→ −→
a2 = || CP ||2 = || OP − OC ||2 = || OP ||2 + || OC ||2 − 2 OP · OC
= r2 + a2 − 2ra cos θ.
Assim,
r2 = 2ra cos θ
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

345. 5.2 ¸˜
Coordenadas Polares e Equacoes Param´ tricas
e 333
y y
P
P
r
r
θ
θ
C x C x
Figura 5.34 – Circunferˆ ncia que passa pelo polo com
e Figura 5.35 – Circunferˆ ncia que passa pelo polo com
e
`
centro no eixo polar a direita `
centro no eixo polar a esquerda
Marco 2012
¸ Reginaldo J. Santos

346. 334 ¸˜
Secoes Cˆ nicas
o
y y
θ
x
P
r
C
C
r
P
θ
x
Figura 5.36 – Circunferˆ ncia que passa pelo polo com
e Figura 5.37 – Circunferˆ ncia que passa pelo polo com
e
centro acima do polo na reta perpendicular ao eixo centro abaixo do polo na reta perpendicular ao eixo
polar que passa pelo polo polar que passa pelo polo
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

347. 5.2 ¸˜
Coordenadas Polares e Equacoes Param´ tricas
e 335
ou
r (r − 2a cos θ ) = 0
¸˜ ´
Logo a equacao em coordenadas polares da circunferˆ ncia e
e
r = 2a cos θ.
(b) Se o raio e igual a a e o centro em coordenadas polares e C = ( a, π ). Se P e
´ ´ ´
um ponto qualquer da circunferˆ ncia, ent˜ o
e a
−→ −→ −→ −→ −→ −→ −→
a2 = || CP ||2 = || OP − OC ||2 = || OP ||2 + || OC ||2 − 2 OP · OC
= r2 + a2 − 2ra cos(π − θ ).
Assim,
r2 = −2ra cos θ
ou
r (r + 2a cos θ ) = 0
¸˜ ´
Logo a equacao em coordenadas polares da circunferˆ ncia e
e
r = −2a cos θ.
(b) Se o centro est´ na reta perpendicular ao eixo polar que passa pelo polo.
a
(a) Se o raio e igual a a e o centro em coordenadas polares e C = ( a, π/2). Se P
´ ´
´
e um ponto qualquer da circunferˆ ncia, ent˜ o
e a
−→ −→ −→ −→ −→ −→ −→
a2 = || CP ||2 = || OP − OC ||2 = || OP ||2 + || OC ||2 − 2 OP · OC
= r2 + a2 − 2ra cos(π/2 − θ ).
Assim,
r2 = 2ra sen θ
Marco 2012
¸ Reginaldo J. Santos

348. 336 ¸˜
Secoes Cˆ nicas
o
ou
r (r − 2a sen θ ) = 0
¸˜ ´
Logo a equacao em coordenadas polares da circunferˆ ncia e
e
r = 2a sen θ.
(b) Se o raio e igual a a e o centro em coordenadas polares e C = ( a, −π/2). Se
´ ´
P e um ponto qualquer da circunferˆ ncia, ent˜ o
´ e a
−→ −→ −→ −→ −→ −→ −→
a2 = || CP ||2 = || OP − OC ||2 = || OP ||2 + || OC ||2 − 2 OP · OC
= r2 + a2 − 2ra cos(−π/2 − θ ).
Assim,
r2 = −2ra sen θ
ou
r (r + 2a sen θ ) = 0
¸˜ ´
Logo a equacao em coordenadas polares da circunferˆ ncia e
e
r = −2a sen θ.
¸˜
Proposicao 5.7. Considere uma circunferˆncia de raio a que passa pelo polo cujo centro est´ no eixo polar ou na reta
e a
perpendicular ao eixo polar que passa pelo polo.
`
(a) Se o centro est´ no eixo polar e a direita do polo, ent˜ o a equa¸ ao polar da circunferˆncia e dada por
a a c˜ e ´
r = 2a cos θ
a`
e se o centro est´ a esquerda do polo, ent˜ o a equa¸ ao polar da circunferˆncia e dada por
a c˜ e ´
r = −2a cos θ.
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

349. 5.2 ¸˜
Coordenadas Polares e Equacoes Param´ tricas
e 337
(b) Se o centro est´ na reta perpendicular ao eixo polar que passa pelo polo e acima do polo, ent˜ o a equa¸ ao polar e
a a c˜ ´
dada por
r = 2a sen θ,
e se est´ abaixo do polo, ent˜ o a equa¸ ao polar da circunferˆncia e dada por
a a c˜ e ´
r = −2a sen θ.
Exemplo 5.4. Uma circunferˆ ncia cuja equacao em coordenadas polares e
e ¸˜ ´
r = −3 cos θ
passa pelo polo, tem raio igual a 3/2 e as coordenadas polares do seu centro s˜ o
a
(3/2, π ).
¸˜
5.2.3 Equacoes Param´ tricas
e
Seja
F ( x, y) = 0 (5.9)
a equacao de uma curva plana C em coordenadas retangulares. Sejam x e y funcoes
¸˜ ¸˜
de uma terceira vari´ vel t em um subconjunto, I , do conjunto dos numeros reais, R,
a ´
ou seja,
x = f (t) e y = g(t), para todo t ∈ I . (5.10)
Se para qualquer valor da vari´ vel t no conjunto I , os valores de x e y determi-
a
¸˜ ¸˜
nados pelas equacoes (5.10) satisfazem (5.9), ent˜ o as equacoes (5.10) s˜ o chamadas
a a
equa¸ oes param´ tricas da curva C e a vari´ vel independente t e chamada parˆ metro.
c˜ e a ´ a
e ¸˜
Dizemos tamb´ m que as equacoes (5.10) formam uma representa¸ ao param´ trica
c˜ e
da curva C . A representacao param´ trica de curvas tem um papel importante no
¸˜ e
tracado de curvas pelo computador.
¸
Marco 2012
¸ Reginaldo J. Santos

350. 338 ¸˜
Secoes Cˆ nicas
o
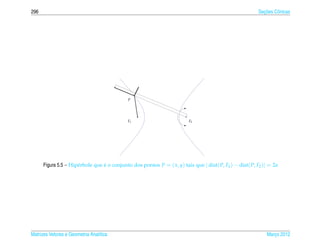
Exemplo 5.5. Seja a um numero real positivo fixo. A circunferˆ ncia de equacao
´ e ¸˜
x 2 + y2 = a2 (5.11)
¸˜
pode ser representada parametricamente pelas equacoes
x = a cos t e y = a sen t, para todo t ∈ [0, 2π ). (5.12)
¸˜
Pois elevando ao quadrado cada uma das equacoes (5.12) e somando os resultados
obtemos
x2 + y2 = a2 cos2 t + a2 sen2 t = a2 .
A circunferˆ ncia definida por (5.11) pode tamb´ m ser representada parametrica-
e e
mente por
x = t e y = a2 − t2 , para todo t ∈ [− a, a]. (5.13)
ou por
x=t e y=− a2 − t2 , para todo t ∈ [− a, a]. (5.14)
Apenas que com (5.13) obtemos somente a parte de cima da circunferˆ ncia e com
e
(5.14) obtemos somente a parte de baixo.
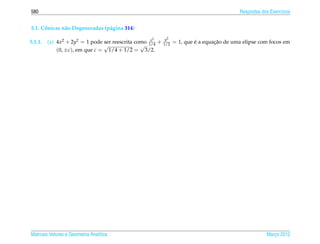
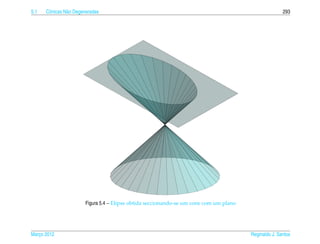
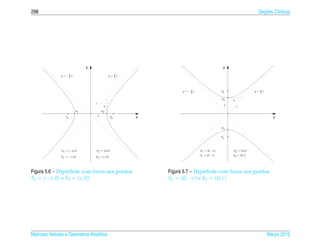
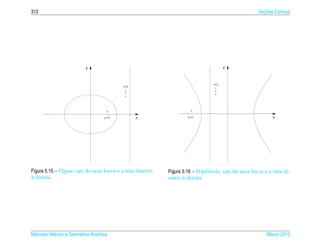
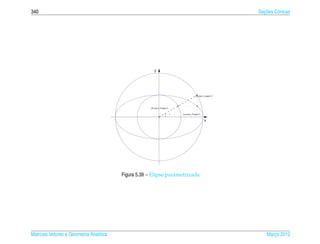
Exemplo 5.6. A elipse de equacao
¸˜
x2 y2
+ 2 =1 (5.15)
a2 b
¸˜
pode ser representada parametricamente pelas equacoes
x = a cos t e y = b sen t, para todo t ∈ [0, 2π ). (5.16)
Pois elevando-se ao quadrado e dividindo-se por a2 a primeira equacao em (5.16),
¸˜
elevando-se ao quadrado e dividindo-se por b2 a segunda equacao em (5.16) e
¸˜
somando-se os resultados obtemos
x2 y2
2
+ 2 = cos2 t + sen2 t = 1.
a b
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

351. 5.2 ¸˜
Coordenadas Polares e Equacoes Param´ tricas
e 339
y
(cos t, sen t)
t
x
Figura 5.38 – Circunferˆ ncia parametrizada
e
Marco 2012
¸ Reginaldo J. Santos

352. 340 ¸˜
Secoes Cˆ nicas
o
y
( a cos t, a sen t)
(b cos t, b sen t)
t ( a cos t, b sen t)
x
Figura 5.39 – Elipse parametrizada
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

353. 5.2 ¸˜
Coordenadas Polares e Equacoes Param´ tricas
e 341
Exemplo 5.7. A hip´ rbole de equacao
e ¸˜
x2 y2
− 2 =1 (5.17)
a2 b
¸˜
pode ser representada parametricamente pelas equacoes
x = a sec t e y = b tan t, para todo t ∈ [0, 2π ), t = π/2, 3π/2. (5.18)
Pois elevando-se ao quadrado e dividindo-se por a2 a primeira equacao em (5.18),
¸˜
elevando-se ao quadrado e dividindo-se por b2 a segunda equacao em (5.18) e
¸˜
subtraindo-se os resultados obtemos
x2 y2
2
− 2 = sec2 t − tan2 t = 1.
a b
¸˜
Vamos apresentar uma outra representacao param´ trica da hip´ rbole. Para isso va-
e e
¸˜
mos definir duas funcoes
et + e−t et − e−t
f 1 (t) = e f 2 (t) = . (5.19)
2 2
A hip´ rbole definida por (5.17) pode, tamb´ m, ser representada parametricamente
e e
por
x = a f 1 (t) e y = b f 2 (t), para todo t ∈ R. (5.20)
Pois elevando-se ao quadrado e dividindo-se por a2 a primeira equacao em (5.20),
¸˜
elevando-se ao quadrado e dividindo-se por b2 a segunda equacao em (5.20) e
¸˜
subtraindo-se os resultados obtemos
x 2 y2 1 2t 1 2t
2
− 2 = ( f 1 (t))2 − ( f 2 (t))2 = e + 2 + e−2t − e − 2 + e−2t = 1. (5.21)
a b 4 4
Marco 2012
¸ Reginaldo J. Santos

354. 342 ¸˜
Secoes Cˆ nicas
o
y
(0, 1)
(0, 1/2)
x
´
Figura 5.40 – Cosseno hiperbolico
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

355. 5.2 ¸˜
Coordenadas Polares e Equacoes Param´ tricas
e 343
y
(0, 1/2)
x
(0, −1/2)
´
Figura 5.41 – Seno hiperbolico
Marco 2012
¸ Reginaldo J. Santos

356. 344 ¸˜
Secoes Cˆ nicas
o
As funcoes f 1 (t) e f 2 (t) definidas por (5.19) recebem o nome de cosseno hiperbolico
¸˜ ´
e seno hiperbolico, respectivamente e s˜ o denotadas por cosh t e senh t. De (5.21)
´ a
¸˜ ´
segue-se a seguinte relacao fundamental entre o cosseno e o seno hiperbolicos
cosh2 t − senh2 t = 1. (5.22)
¸˜
e a representacao param´ trica (5.20) pode ser escrita como
e
x = a cosh t e y = b senh t, para todo t ∈ R. (5.23)
Tamb´ m
e
x = − a cosh t e y = b senh t, para todo t ∈ R. (5.24)
´ ¸˜
e uma representacao param´ trica da hip´ rbole (5.17). Apenas que com (5.23) obte-
e e
mos somente o ramo direito da hip´ rbole e com (5.24), somente o ramo esquerdo.
e
Exemplo 5.8. Vamos mostrar que a parametrizacao de uma curva em relacao a qual
¸˜ ¸˜
sabemos sua equacao em coordenadas polares r = f (θ ) pode ser feita da seguinte
¸˜
forma
x = f (t) cos t e y = f (t) sen t. (5.25)
¸˜ ´
A equacao da curva em coordenadas cartesianas e
x2 + y2 = f (θ ( x, y)), se f (θ ( x, y)) ≥ 0
− x 2 + y2 = f ( θ ( x, y )), se f ( θ ( x, y )) < 0.
ou
x2 + y2 = | f (θ ( x, y))|. (5.26)
¸˜
Para a parametrizacao (5.25) temos que
x2 + y2 − | f (θ ( x, y))| = ( f (t))2 cos2 t + ( f (t))2 sen2 t − | f (t)| = 0.
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

357. 5.2 ¸˜
Coordenadas Polares e Equacoes Param´ tricas
e 345
y y
( a cos t, a sen t)
(− a cosh t, b senh t)
(b, b tan t) ( a sec t, b tan t)
( a cosh t, b senh t)
t
x x
Figura 5.42 – Hip´ rbole parametrizada usando se-
e Figura 5.43 – Hip´ rbole parametrizada usando as
e
cante e tangente ¸˜ ´
funcoes hiperbolicas
Marco 2012
¸ Reginaldo J. Santos

358. 346 ¸˜
Secoes Cˆ nicas
o
O que mostra que (5.25) e uma parametrizacao para (5.26) e portanto para r = f (θ ).
´ ¸˜
Por exemplo,
e cos t e sen t
x= e y=
1 + e cos t 1 + e cos t
e uma parametrizacao de uma conica com excentricidade e > 0, reta diretriz locali-
´ ¸˜ ˆ
`
zada a direita a uma distˆ ncia igual a 1 e um dos focos na origem.
a
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

359. 5.2 ¸˜
Coordenadas Polares e Equacoes Param´ tricas
e 347
y
y
( 1+cos t t , 1+sen t t )
e
e cos
e
e cos
( 1+cos t t , 1+sen t t )
e
e cos
e
e cos ( e cos t , e sen t )
1+e cos t 1+e cos t
t
t
t
x
x
Figura 5.44 – Elipse com foco na origem parametri- Figura 5.45 – Hip´ rbole com foco na origem parame-
e
´ ´
trizada usando a sua formula em coordenadas pola-
zada usando a sua formula em coordenadas polares
res
Marco 2012
¸ Reginaldo J. Santos

360. 348 ¸˜
Secoes Cˆ nicas
o
Exerc´cios Num´ ricos (respostas na p´ gina 587)
ı e a
¸˜ ¸˜
5.2.1. Transformar a equacao em coordenadas retangulares em uma equacao em coordenadas polares:
(a) x2 + y2 = 4 (c) x2 + y2 − 2y = 0
(b) x2 − y2 = 4 (d) x2 − 4y − 4 = 0
¸˜ ¸˜
5.2.2. Transformar a equacao em coordenadas polares em uma equacao em coordenadas retangulares:
2 3
(a) r = (d) r =
1 − 3 cos θ 2 + sen θ
(b) r = 4 sen θ (e) r = tan θ
(c) r = 9 cos θ (f) r ( a cos θ + b sen θ ) − c = 0
ˆ ¸˜ ´ ¸˜
5.2.3. Identificar a conica cuja equacao em coordenadas polares e dada. Determine a excentricidade, a equacao
da diretriz, a distˆ ncia da diretriz ao foco e as coordenadas polares de dois v´ rtices:
a e
5 3
(a) r = (c) r =
2 − 2 cos θ 2 + 4 cos θ
6 4
(b) r = (d) r =
3 + sen θ 2 − 3 cos θ
¸˜
5.2.4. Determine o raio e e as coordenadas polares do centro da circunferˆ ncia cuja equacao em coordenadas
e
´
polares e dada:
3
(a) r = 4 cos θ (c) r = 2 cos θ
(b) r = −3 sen θ (d) r = − 4 sen θ
3
˜
5.2.5. Descreva as regioes a seguir usando coordenadas polares:
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

361. 5.2 ¸˜
Coordenadas Polares e Equacoes Param´ tricas
e 349
y
y
5
5 4
3
4 2 x2+y2 = 18
1
3 x
2 2
x +y = 25 -5 -4 -3 -2 -1 1 2 3 4 5
-1
2
-2
1 -3
x -4
-5
1 2 3 4 5
(a) (b)
y y
3 y = x/2
5
2
4
1 (x-2)2+y2 = 4
x
3 y=x
1 2 3 4 5 6
2
-1
1 x2+y2 = 4 y = x/2 -2
x
-3
1 2 3 4 5
(c) (d)
Marco 2012
¸ Reginaldo J. Santos

362. 350 ¸˜
Secoes Cˆ nicas
o
Exerc´cios Teoricos
ı ´
5.2.6. A equacao da trajetoria de uma part´cula lancada do ponto P0 = (0, 0), com velocidade v0 , fazendo um
¸˜ ´ ı ¸
angulo α com o eixo x e sujeita apenas a acao da aceleracao da gravidade g e dada por
ˆ ¸˜ ¸˜ ´
g
y = (tan α) x − x2 .
2v2 cos2
0 α
g 2
Mostre que x = (v0 cos α) t e y = (v0 sen α) t − t s˜ o equacoes param´ tricas da trajetoria da part´cula.
a ¸˜ e ´ ı
2
5.2.7. Se o centro de uma circunferˆ ncia que passa pelo polo e ( a, α), mostre que sua equacao em coordenadas
e ´ ¸˜
polares e r = 2a cos(θ − α).
´
de
5.2.8. Se a conica de equacao r =
ˆ ¸˜ representa uma par´ bola, determine as coordenadas polares do
a
1 − e cos θ
¸˜
seu v´ rtice e a equacao em coordenadas polares da reta diretriz.
e
de
5.2.9. Se a conica de equacao r =
ˆ ¸˜ representa uma elipse, mostre que o comprimento do seu eixo
1 + e cos θ
2de
menor e √
´ .
1 − e2
¸˜
5.2.10. Mostre que a equacao em coordenadas polares de uma elipse com um dos focos no polo, que tem eixo
maior igual a 2a e excentricidade e e
´
a (1 − e2 )
r= .
1 − e cos θ
5.2.11. Considere uma conica com excentricidade e > 0 (que n˜ o e uma circunferˆ ncia), que tem um foco F no
ˆ a ´ e
2
polo e a reta diretriz s e paralela ou perpendicular ou eixo polar, com d = dist(s, F ). Seja p = 1dee2 , se a
´ −
de2
reta s estiver a direita do foco F e p =
` e2 −1
, se a reta s estiver a esquerda do foco F.
`
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

363. 5.2 ¸˜
Coordenadas Polares e Equacoes Param´ tricas
e 351
(a) Se a reta diretriz correspondente a F e perpendicular ao eixo polar e est´ a direita ou a esquerda do
´ a` `
¸˜ ˆ ´
polo, ent˜ o a equacao cartesiana da conica e
a
( x + p )2 y2
p2
+ p2 (1− e2 )
=1
e2 e2
(b) Se a reta diretriz correspondente a F e paralela ao eixo polar e est´ acima ou abaixo do polo, ent˜ o
´ a a
¸˜ ˆ
a equacao cartesiana da conica e´
x2 ( y + p )2
2 2 +
p (1− e ) 2 =1p
e2 e2
¸˜
5.2.12. Mostre que um espelho el´ptico, reflete na direcao de um foco, os raios que incidem na elipse vindo do
ı
outro foco, seguindo os seguintes passos:
x2 y2
(a) Considere a elipse + 2 = 1. Usando o fato de que um ponto da elipse pode ser escrito na
a2 b
forma P = ( a cos t, b sen t), para t ∈ [0, 2π ) e que a inclinacao da reta tangente a elipse neste ponto
¸˜ `
dy b cos t
´
e =− , mostre que a equacao da reta tangente a elipse em P e
¸˜ ` ´
dx a sen t
b cos t
y = b sen t − ( x − a cos t), para t = 0, π,
a sen t
e que a equacao da reta que passa por F2 e e paralela ao raio que passa por F1 depois de ser refletido
¸˜ ´
em P e´
b sen t
y= ( x − c ).
c + a cos t
(b) Mostre que a intersecao da reta tangente a elipse que passa por P e a reta que passa por F2 e e
¸˜ ` ´
paralela ao raio que passa por F1 depois de ser refletido em P e o ponto
´
a(c sen2 t + a cos t + c) b sen t( a − c cos t)
P1 = ,
a + c cos t a + c cos t
Marco 2012
¸ Reginaldo J. Santos

364. 352 ¸˜
Secoes Cˆ nicas
o
(c) Mostre que dist( P, F2 ) = dist( P1 , F2 ) = a − c cos t. Logo o triˆ ngulo PF2 P1 e isosceles e assim o
a ´ ´
angulo de reflex˜ o do raio que passa por F1 depois de ser refletido em P, α1 , e o angulo de incidˆ ncia
ˆ a ˆ e
do raio que se reflete em P vindo de F2 , α2 , s˜ o iguais. Portanto o raio que vem de F2 e se reflete em
a
P necessariamente passa por F1 (veja a Figura 5.46).
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

365. 5.2 ¸˜
Coordenadas Polares e Equacoes Param´ tricas
e 353
y
P = ( a cos(t), b sen(t))
α1
α2
α1 P1
F1 = (−c, 0) F2 = (c, 0) x
¸˜
Figura 5.46 – Elipse refletindo, na direcao de um foco, os raios que incidem na elipse vindo do outro foco
Marco 2012
¸ Reginaldo J. Santos

366. 354 ¸˜
Secoes Cˆ nicas
o
¸˜
Figura 5.47 – Espelho el´ptico refletindo, na direcao de um foco, os raios que incidem vindo do outro foco
ı
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

367. 5.2 ¸˜
Coordenadas Polares e Equacoes Param´ tricas
e 355
´ ¸˜
5.2.13. Mostre que um espelho hiperbolico, reflete na direcao de um foco, os raios que incidem na hip´ rbole na
e
¸˜
direcao do outro foco, seguindo os seguintes passos:
x 2 y2
(a) Considere a hip´ rbole
e − 2 = 1. Usando o fato de que um ponto do ramo esquerdo da hip´ rbole e
a2 b
pode ser escrito na forma P = (− a sec t, b tan t), para t ∈ (−π/2, π/2) e que a inclinacao da reta
¸˜
dy b
` ´
tangente a hip´ rbole neste ponto e
e =− ¸˜ `
, mostre que a equacao da reta tangente a hip´ rbole
e
dx a sen t
em P e´
b
y = b tan t − ( x + a sec t), para t = 0,
a sen t
e que a equacao da reta que passa por F2 e e paralela ao raio que incide na direcao de F1 e se reflete
¸˜ ´ ¸˜
em P e´
b tan t
y= ( x − c ).
c − a sec t
(b) Mostre que a intersecao da reta tangente a hip´ rbole que passa por P e a reta que passa por F2 e e
¸˜ ` e ´
paralela ao raio que incide na direcao de F1 e se reflete em P e o ponto
¸˜ ´
a(2c cos2 t − a cos t − c) b sen t( a cos t + c)
P1 = ,
cos t( a cos t − c) cos t( a cos t − c)
(c) Mostre que dist( P, F2 ) = dist( P1 , F2 ) = a + c sec t. Logo o triˆ ngulo PF2 P1 e isosceles e assim o
a ´ ´
angulo de incidˆ ncia do raio que incide na direcao de F1 e se reflete em P, α1 , e o angulo de reflex˜ o
ˆ e ¸˜ ˆ a
do raio que se reflete em P na direcao de F2 , α2 , s˜ o iguais. Portanto o raio que incide na direcao de
¸˜ a ¸˜
F1 e se reflete em P necessariamente passa por F2 (veja as Figuras 5.48 e 5.49)
Marco 2012
¸ Reginaldo J. Santos

368. 356 ¸˜
Secoes Cˆ nicas
o
y
α1
P = (− a sec t, b tan t)
α2
F2 = (c, 0)
F1 = (−c, 0)
x
α1
P1
¸˜ ¸˜
Figura 5.48 – Hip´ rbole refletindo, na direcao de um foco, os raios que incidem na hip´ rbole na direcao do outro
e e
foco
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

369. 5.2 ¸˜
Coordenadas Polares e Equacoes Param´ tricas
e 357
y
α1
α2
P = (− a sec t, b tan t)
α1 α2
F2 = (c, 0)
F1 = (−c, 0)
x
α1
P1
¸˜ ¸˜
Figura 5.49 – Hip´ rbole refletindo, na direcao de um foco, os raios que incidem na hip´ rbole na direcao do outro
e e
foco
Marco 2012
¸ Reginaldo J. Santos

370. 358 ¸˜
Secoes Cˆ nicas
o
´ ¸˜
Figura 5.50 – Espelho maior parabolico refletindo na direcao do foco, em seguida os raios s˜ o refletidos por um
a
´ ¸˜
espelho hiperbolico na direcao do outro foco da hip´ rbole
e
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

371. 6
Superf´cies e Curvas no Espaco
ı ¸
6.1 Qu´ dricas
a
¸˜
Nesta secao estudaremos as superf´cies que podem ser representadas pelas equa¸ oes
ı c˜
quadr´ ticas nas vari´ veis x, y e z, ou seja, da forma
a a
ax2 + by2 + cz2 + dxy + exz + f yz + gx + hy + iz + j = 0,
em que a, b, c, d, e, f , g, h, i, j ∈ R, com a, b, c, d, e, f n˜ o simultaneamente nulos. Va-
a
mos nos limitar neste cap´tulo ao estudo de casos especiais da equacao acima.
ı ¸˜
359

372. 360 Superf´cies e Curvas no Espaco
ı ¸
z
x y
x2 y2 z2
¸˜
Figura 6.1 – Elipsoide de equacao a2
+ b2
+ c2
=1
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

373. 6.1 Qu´ dricas
a 361
z
x y
Figura 6.2 – Elipsoide e intersecoes com os planos z = k
¸˜
Marco 2012
¸ Reginaldo J. Santos

374. 362 Superf´cies e Curvas no Espaco
ı ¸
6.1.1 Elipsoide
´
Um elipsoide e um conjunto de pontos que em algum sistema de coordenadas satis-
¸˜
faz a equacao
x2 y2 z2
2
+ 2 + 2 = 1, (6.1)
a b c
em que a, b e c s˜ o numeros reais positivos.
a ´
Observe que se o ponto ( x, y, z) satisfaz (6.1), ent˜ o o ponto sim´ trico em relacao
a e ¸˜
ao plano xy, ( x, y, −z), tamb´ m satisfaz, por isso dizemos que o elipsoide (6.1) e
e ´
sim´ trico em relacao ao plano xy. Tamb´ m ( x, −y, z) satisfaz (6.1), por isso dizemos
e ¸˜ e
´ ¸˜
que o elipsoide (6.1) e sim´ trico em relacao ao plano xz. O mesmo acontece com
e
(− x, y, z), por isso dizemos que o elipsoide (6.1) e sim´ trico em relacao ao plano
´ e ¸˜
yz. Se o ponto ( x, y, z) satisfaz (6.1), ent˜ o o ponto sim´ trico em relacao ao eixo z,
a e ¸˜
(− x, −y, z), tamb´ m satisfaz, por isso dizemos que o elipsoide (6.1) e sim´ trico em
e ´ e
relacao ao eixo z. O mesmo acontece com (− x, y, −z), por isso dizemos que o elip-
¸˜
soide (6.1) e sim´ trico em relacao ao eixo y. O mesmo acontece com ( x, −y, −z),
´ e ¸˜
´ ¸˜
por isso dizemos que o elipsoide (6.1) e sim´ trico em relacao ao eixo x. Final-
e
mente se o ponto ( x, y, z) satisfaz (6.1), ent˜ o o ponto sim´ trico em relacao a origem,
a e ¸˜ `
(− x, −y, −z), tamb´ m satisfaz, por isso dizemos que o elipsoide (6.1) e sim´ trico em
e ´ e
¸˜ `
relacao a origem.
Se |k| < c, o plano z = k intercepta o elipsoide (6.1) segundo a elipse
x2 y2
+ = 1, z = k.
k2 k2
a2 1 − c2
b2 1 − c2
Observe que os eixos da elipse diminuem a medida que |k| aumenta.
`
As intersecoes do elipsoide (6.1) com o plano x = k, para |k| < a e com o plano
¸˜
y = k, para |k| < b, s˜ o tamb´ m elipses. Se a = b = c, o elipsoide e uma esfera de
a e ´
raio r = a = b = c.
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

375. 6.1 Qu´ dricas
a 363
z
x y
Figura 6.3 – Elipsoide e intersecoes com os planos y = k
¸˜
Marco 2012
¸ Reginaldo J. Santos

376. 364 Superf´cies e Curvas no Espaco
ı ¸
z
x y
Figura 6.4 – Elipsoide e intersecoes com os planos x = k
¸˜
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

377. 6.1 Qu´ dricas
a 365
6.1.2 Hiperboloide
Hiperboloide de Uma Folha
´
Um hiperboloide de uma folha e um conjunto de pontos que em algum sistema de
¸˜
coordenadas satisfaz a equacao
x2 y2 z2
+ 2 − 2 = 1, (6.2)
a2 b c
em que a, b e c s˜ o numeros reais positivos.
a ´
´
Observe que o hiperboloide de uma folha (6.2) e sim´ trico em relacao aos planos
e ¸˜
coordenados, aos eixos coordenados e a origem. Pois, se ( x, y, z) satisfaz (6.2), ent˜ o
` a
(− x, y, z), ( x, −y, z), ( x, y, −z), (− x, −y, z), ( x, −y, −z), (− x, y, −z) e (− x, −y, −z)
tamb´ m satisfazem.
e
O plano z = k intercepta o hiperboloide de uma folha (6.2) segundo a elipse
x2 y2
+ = 1, z = k.
k2 k2
a2 1 + c2
b2 1 + c2
Observe que os eixos da elipse aumentam a medida que |k| cresce.
`
O plano y = k intercepta o hiperboloide de uma folha (6.2) segundo uma curva cuja
¸˜ ´
equacao e
x2 z2 k2
2
− 2 = 1 − 2 , y = k.
a c b
Se |k/b| = 1, ent˜ o a intersecao e uma hip´ rbole e se |k/b| = 1, ent˜ o a intersecao e
a ¸˜ ´ e a ¸˜ ´
um par de retas concorrentes.
¸˜ ¸˜
Consideracoes semelhantes s˜ o v´ lidas para a intersecao do hiperboloide de uma
a a
folha (6.2) com o plano x = k.
¸˜
As equacoes
x2 y2 z2
2
− 2 + 2 =1
a b c
Marco 2012
¸ Reginaldo J. Santos

378. 366 Superf´cies e Curvas no Espaco
ı ¸
z
x y
x2 y2 z2
¸˜
Figura 6.5 – Hiperboloide de uma folha de equacao a2
+ b2
− c2
=1
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

379. 6.1 Qu´ dricas
a 367
z
x y
Figura 6.6 – Hiperboloide de uma folha e intersecoes com os planos z = k
¸˜
Marco 2012
¸ Reginaldo J. Santos

380. 368 Superf´cies e Curvas no Espaco
ı ¸
e
x2 y2 z2
2
−
+ 2 + 2 =1
a b c
tamb´ m representam hiperboloides de uma folha.
e
Hiperboloide de Duas Folhas
´
Um hiperboloide de duas folhas e um conjunto de pontos que em algum sistema
¸˜
de coordenadas satisfaz a equacao
x2 y2 z2
− − 2 + 2 = 1, (6.3)
a2 b c
em que a, b e c s˜ o numeros reais positivos.
a ´
´ ¸˜
Observe que o hiperboloide de duas folhas (6.3) e sim´ trico em relacao aos planos
e
coordenados, aos eixos coordenados e a origem. Pois, se ( x, y, z) satisfaz (6.3), ent˜ o
` a
(− x, y, z), ( x, −y, z), ( x, y, −z), (− x, −y, z), ( x, −y, −z), (− x, y, −z) e (− x, −y, −z)
tamb´ m satisfazem.
e
O plano z = k, para |k| > c, intercepta o hiperboloide de duas folhas (6.3) segundo a
elipse
x2 y2
2
+ 2
= 1, z = k.
a2 k2 − 1
c
b2 k2 − 1
c
O plano y = k intercepta o hiperboloide de duas folhas (6.3) segundo a hip´ rbole
e
x2 z2
− + = 1, y = k.
k2 k2
a2 1 + b2
c2 1 + b2
A intersecao do hiperboloide de duas folhas (6.3) com o plano x = k e tamb´ m uma
¸˜ ´ e
hip´ rbole.
e
¸˜
As equacoes
x2 y2 z2
2
− 2 − 2 =1
a b c
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

381. 6.1 Qu´ dricas
a 369
z
x y
Figura 6.7 – Hiperboloide de uma folha e intersecoes com os planos y = k
¸˜
Marco 2012
¸ Reginaldo J. Santos

382. 370 Superf´cies e Curvas no Espaco
ı ¸
z
x y
Figura 6.8 – Hiperboloide de uma folha e intersecoes com os planos x = k
¸˜
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

383. 6.1 Qu´ dricas
a 371
z
x y
Figura 6.9 – Hiperboloide de duas folhas
Marco 2012
¸ Reginaldo J. Santos

384. 372 Superf´cies e Curvas no Espaco
ı ¸
z
x y
Figura 6.10 – Hiperboloide de duas folhas e intersecoes com os planos z = k
¸˜
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

385. 6.1 Qu´ dricas
a 373
e
x2 y2 z2
− 2
+ 2 − 2 =1
a b c
tamb´ m representam hiperboloides de duas folhas.
e
Marco 2012
¸ Reginaldo J. Santos

386. 374 Superf´cies e Curvas no Espaco
ı ¸
z
x y
Figura 6.11 – Hiperboloide de duas folhas e intersecoes com os planos y = k
¸˜
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

387. 6.1 Qu´ dricas
a 375
z
x y
Figura 6.12 – Hiperboloide de duas folhas e intersecoes com os planos x = k
¸˜
Marco 2012
¸ Reginaldo J. Santos

388. 376 Superf´cies e Curvas no Espaco
ı ¸
6.1.3 Paraboloide
Paraboloide El´ptico
ı
´
Um paraboloide el´ptico e um conjunto de pontos que em algum sistema de coor-
ı
¸˜
denadas satisfaz a equacao
x2 y2
cz = + 2, (6.4)
a2 b
em que a, b e c s˜ o numeros reais, sendo a e b positivos.
a ´
O paraboloide el´ptico (6.4) e sim´ trico em relacao aos planos xz e yz. Pois, se ( x, y, z)
ı ´ e ¸˜
satisfaz (6.4), ent˜ o ( x, −y, z) e (− x, y, z) tamb´ m satisfazem. Ele tamb´ m e sim´ trico
a e e ´ e
em relacao ao eixo z, pois se ( x, y, z) satisfaz (6.4), ent˜ o (− x, −y, z) tamb´ m satisfaz.
¸˜ a e
A intersecao do paraboloide el´ptico (6.4) com o plano z = k, para k tal que ck > 0, e
¸˜ ı ´
a elipse
x2 y2
+ = 1, z = k.
cka2 ckb2
A intersecao do paraboloide el´ptico (6.4) com plano x = k e a par´ bola
¸˜ ı ´ a
k2 y2
z= + 2, x = k.
ca2 cb
A intersecao do paraboloide el´ptico (6.4) com plano y = k tamb´ m e uma par´ bola.
¸˜ ı e ´ a
¸˜
As equacoes
y2 z2
ax = 2 + 2
b c
e
x2 z2
by = 2 + 2
a c
tamb´ m representam paraboloides el´pticos.
e ı
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

389. 6.1 Qu´ dricas
a 377
z
x y
x2 y2
Figura 6.13 – Paraboloide el´ptico de equacao cz =
ı ¸˜ a2
+ b2
, para c > 0
Marco 2012
¸ Reginaldo J. Santos

390. 378 Superf´cies e Curvas no Espaco
ı ¸
z
x y
Figura 6.14 – Paraboloide el´ptico e intersecoes com os planos z = k
ı ¸˜
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

391. 6.1 Qu´ dricas
a 379
z
x y
Figura 6.15 – Paraboloide el´ptico e intersecoes com os planos y = k
ı ¸˜
Marco 2012
¸ Reginaldo J. Santos

392. 380 Superf´cies e Curvas no Espaco
ı ¸
z
x y
Figura 6.16 – Paraboloide el´ptico e intersecoes com os planos x = k
ı ¸˜
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

393. 6.1 Qu´ dricas
a 381
z
y
x
x2 y2
Figura 6.17 – Paraboloide hiperbolico de equacao cz =
´ ¸˜ a2
− b2
, para c < 0
Marco 2012
¸ Reginaldo J. Santos

394. 382 Superf´cies e Curvas no Espaco
ı ¸
z
y
x
Figura 6.18 – Paraboloide hiperbolico e intersecoes com os planos z = k
´ ¸˜
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

395. 6.1 Qu´ dricas
a 383
Paraboloide Hiperb´ lico
o
´
Um paraboloide hiperbolico e um conjunto de pontos que em algum sistema de
´
¸˜
coordenadas satisfaz a equacao
x2 y2
cz = 2
− 2, (6.5)
a b
em que a, b e c s˜ o numeros reais, sendo a e b positivos.
a ´
´ ´ ¸˜
O paraboloide hiperbolico (6.5) e sim´ trico em relacao aos planos xz e yz. Pois, se
e
( x, y, z) satisfaz (6.5), ent˜ o ( x, −y, z) e (− x, y, z) tamb´ m satisfazem. Ele tamb´ m
a e e
e sim´ trico em relacao ao eixo z, pois se ( x, y, z) satisfaz (6.5), ent˜ o (− x, −y, z)
´ e ¸˜ a
tamb´ m satisfaz.
e
A intersecao do plano z = k com o paraboloide hiperbolico (6.5) e dada por
¸˜ ´ ´
x2 y2
2
− 2 = k, z = k,
ca cb
que representa uma hip´ rbole, se k = 0 e um par de retas, se k = 0.
e
A intersecao do paraboloide hiperbolico (6.5) com plano y = k e a par´ bola
¸˜ ´ ´ a
x2 k2
z= 2
− 2, y=k
ca cb
que tem concavidade para cima se c > 0 e concavidade para baixo se c < 0.
A intersecao do paraboloide hiperbolico com plano x = k e a par´ bola
¸˜ ´ ´ a
y2 k2
z=− + 2, x=k
cb2 ca
que tem concavidade para baixo se c > 0 e concavidade para cima se c < 0. O
´ ´
paraboloide hiperbolico e tamb´ m chamado sela.
e
¸˜
As equacoes
y2 z2
ax = 2 − 2
b c
Marco 2012
¸ Reginaldo J. Santos

396. 384 Superf´cies e Curvas no Espaco
ı ¸
e
x2 z2
by = 2
− 2
a c
´
tamb´ m representam paraboloides hiperbolicos.
e
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

397. 6.1 Qu´ dricas
a 385
z
y
x
Figura 6.19 – Paraboloide hiperbolico e intersecoes com os planos y = k
´ ¸˜
Marco 2012
¸ Reginaldo J. Santos

398. 386 Superf´cies e Curvas no Espaco
ı ¸
z
y
x
Figura 6.20 – Paraboloide hiperbolico e intersecoes com os planos x = k
´ ¸˜
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

399. 6.1 Qu´ dricas
a 387
6.1.4 Cone El´ptico
ı
´ ¸˜
Um cone el´ptico e um conjunto de pontos que satisfaz a equacao
ı
x2 y2
z2 = + 2, (6.6)
a2 b
em que a e b s˜ o numeros reais positivos, em algum sistema de coordenadas. Se
a ´
a = b, o cone e chamado cone circular.
´
´ ¸˜
Observe que o cone el´ptico (6.6) e sim´ trico em relacao aos planos coordenados,
ı e
aos eixos coordenados e a origem. Pois, se ( x, y, z) satisfaz (6.6), ent˜ o (− x, y, z),
` a
( x, −y, z), ( x, y, −z), (− x, −y, z), ( x, −y, −z), (− x, y, −z) e (− x, −y, −z) tamb´ m sa-
e
tisfazem.
A intersecao do cone el´ptico (6.6) com o plano z = k, para k = 0, e a elipse
¸˜ ı ´
x2 y2
+ 2 2 = 1, z = k.
a2 k 2 b k
Observe que os eixos da elipse crescem a medida que |k| aumenta.
`
Os planos xz e yz cortam o cone el´ptico (6.6) segundo as retas
ı
x = ± az, y = 0 e y = ±bz, x = 0,
respectivamente.
A intersecao do cone el´ptico (6.6) com o plano y = k, para k = 0, e a hip´ rbole
¸˜ ı ´ e
z2 x2
− 2 2 2 = 1, y = k.
k2 /b2 a k /b
A intersecao do cone el´ptico (6.6) com o plano x = k, para k = 0, e a hip´ rbole
¸˜ ı ´ e
z2 y2
− = 1, x = k.
k2 /a2 b2 k2 /a2
Marco 2012
¸ Reginaldo J. Santos

400. 388 Superf´cies e Curvas no Espaco
ı ¸
z
x
y
x2 y2
¸˜
Figura 6.21 – Cone el´ptico de equacao
ı z2 = a2
+ b2
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

401. 6.1 Qu´ dricas
a 389
z
x
y
Figura 6.22 – Cone el´ptico e intersecoes com os planos z = k
ı ¸˜
Marco 2012
¸ Reginaldo J. Santos

402. 390 Superf´cies e Curvas no Espaco
ı ¸
¸˜
As equacoes
y2 z2 x2 z2
x2 = 2
+ 2 e y2 = 2
+ 2
b c a c
tamb´ m representam cones el´pticos.
e ı
6.1.5 Cilindro Qu´ drico
a
a ´
Um cilindro qu´ drico e um conjunto de pontos do espaco, que em algum sistema
¸
¸˜
de coordenadas satisfaz a equacao
f ( x, y) = 0 (6.7)
em que f ( x, y) = 0 e a equacao de uma conica no plano xy.
´ ¸˜ ˆ
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

403. 6.1 Qu´ dricas
a 391
z
x
y
Figura 6.23 – Cone el´ptico e intersecoes com os planos y = k
ı ¸˜
Marco 2012
¸ Reginaldo J. Santos

404. 392 Superf´cies e Curvas no Espaco
ı ¸
z
x
y
Figura 6.24 – Cone el´ptico e intersecoes com os planos x = k
ı ¸˜
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

405. 6.1 Qu´ dricas
a 393
z
x y
x2 y2
¸˜
Figura 6.25 – Cilindro el´ptico de equacao
ı a2
+ b2
=1
Marco 2012
¸ Reginaldo J. Santos

406. 394 Superf´cies e Curvas no Espaco
ı ¸
z
x y
x2 y2
´ ¸˜
Figura 6.26 – Cilindro hiperbolico de equacao a2
− b2
=1
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

407. 6.1 Qu´ dricas
a 395
z
x y
y2 x2
´ ¸˜
Figura 6.27 – Cilindro hiperbolico de equacao a2
− b2
=1
Marco 2012
¸ Reginaldo J. Santos

408. 396 Superf´cies e Curvas no Espaco
ı ¸
z
x
y
Figura 6.28 – Cilindro parabolico de equacao y2 = 4px, p > 0
´ ¸˜
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

409. 6.1 Qu´ dricas
a 397
z
x
y
Figura 6.29 – Cilindro parabolico de equacao x2 = 4py, p > 0
´ ¸˜
Marco 2012
¸ Reginaldo J. Santos

410. 398 Superf´cies e Curvas no Espaco
ı ¸
Chamamos o cilindro qu´ drico de cilindro el´ptico, se a conica de equacao f ( x, y) =
a ı ˆ ¸˜
0 e uma elipse. Por exemplo, a equacao x2 + 2y2 = 1 representa uma elipse no plano,
´ ¸˜
enquanto representa um cilindro el´ptico no espaco. Chamamos o cilindro qu´ drico
ı ¸ a
de cilindro hiperbolico, se a conica de equacao f ( x, y) = 0 e uma hip´ rbole. Por
´ ˆ ¸˜ ´ e
exemplo, a equacao x2 − 2y2 = 1 representa uma hip´ rbole no plano, enquanto
¸˜ e
´
representa um cilindro hiperbolico no espaco. Chamamos o cilindro qu´ drico de
¸ a
cilindro parabolico, se a conica de equacao f ( x, y) = 0 e uma par´ bola. Por exem-
´ ˆ ¸˜ ´ a
plo, a equacao x2 = 4y representa uma par´ bola no plano, enquanto representa um
¸˜ a
´
cilindro parabolico no espaco.
¸
A intersecao do plano z = k com o cilindro e a conica que o originou, chamada
¸˜ ´ ˆ
diretriz do cilindro:
f ( x, y) = 0, z = k.
Se a equacao f ( x, k ) = 0 tem m solucoes (m = 0, 1 ou 2), ent˜ o o plano y = k
¸˜ ¸˜ a
intercepta a superf´cie segundo m retas
ı
f ( x, y) = 0, y = k.
Consideracoes semelhantes s˜ o v´ lidas para a intersecao com o plano x = k.
¸˜ a a ¸˜
¸˜
As equacoes
g( x, z) = 0 e h(y, z) = 0
tamb´ m representam cilindros qu´ dricos desde que g( x, z) = 0 e h(y, z) = 0 sejam
e a
¸˜ ˆ
equacoes de conicas nos planos xz e yz, respectivamente.
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

411. 6.1 Qu´ dricas
a 399
Exerc´cios Num´ ricos (respostas na p´ gina 589)
ı e a
¸˜
6.1.1. Reduzir cada uma das equacoes de forma a identificar a qu´ drica que ela representa e faca um esboco do
a ¸ ¸
seu gr´ fico:
a
(a) 4x2 − 2y2 + z2 = 1 (c) x2 − 9y2 = 9
(b) x 2 + y + z2 = 0 (d) 4x2 − 9y2 − 36z = 0
6.1.2. Obtenha a equacao do lugar geom´ trico dos pontos equidistantes do plano π : x = 2 e do ponto P =
¸˜ e
(−2, 0, 0). Que conjunto e este?
´
¸˜ ¨
6.1.3. Obtenha uma equacao do lugar geom´ trico dos pontos que equidistam das retas
e
r : ( x, y, z) = (0, −1, 0) + t(1, 0, 0) e s : ( x, y, z) = (0, 1, 0) + t(0, 0, 1).
´
Que lugar geom´ trico e este?
e
6.1.4. Determine a equacao do lugar geom´ trico dos pontos P = ( x, y, z) tais que a soma das distˆ ncias de P
¸˜ e a
aos dois pontos (2, 0, 0) e (−2, 0, 0) e igual a 6. Que lugar geom´ trico e este?
´ e ´
6.1.5. Determine a equacao do lugar geom´ trico dos pontos P = ( x, y, z) tais que o modulo da diferenca entre
¸˜ e ´ ¸
as as distˆ ncias de P = ( x, y, z) aos dois pontos (2, 0, 0) e (−2, 0, 0) e igual a 3. Que lugar geom´ trico e
a ´ e ´
este?
Marco 2012
¸ Reginaldo J. Santos

412. 400 Superf´cies e Curvas no Espaco
ı ¸
6.2 ı ı o ¸˜
Superf´cies Cil´ndricas, Cˆ nicas e de Revolucao
6.2.1 Superf´cies Cil´ndricas
ı ı
ı ı ´
Uma superf´cie cil´ndrica e uma superf´cie que pode ser obtida quando uma reta,
ı
chamada geratriz, se move paralelamente passando por uma curva fixa, chamada
diretriz.
Suponhamos que a curva diretriz da superf´cie cil´ndrica S esteja no plano xy e tenha
ı ı
¸˜
equacao neste plano dada por
f ( x, y) = 0 (6.8)
a ´
e que as retas geratrizes sejam paralelas a um vetor que n˜ o e paralelo ao plano xy,
digamos V = ( a, b, 1). Seja P = ( x, y, z) um ponto qualquer sobre S e P = ( x , y , 0)
um ponto do plano xy que est´ na reta geratriz que passa por P. O ponto ( x, y, z)
a
−→
pertence a S se, e somente se, o vetor P P e paralelo a V e P e um ponto da curva
´ ´
diretriz, ou seja,
−→
P P= λV e f ( x , y ) = 0,
´
que e equivalente a
( x − x , y − y , z) = λ( a, b, 1) e f ( x , y ) = 0.
Destas equacoes obtemos que λ = z, x = x − az e y = y − bz. Assim a equacao da
¸˜ ¸˜
superf´cie cil´ndrica S que tem curva diretriz no plano xy com equacao (6.8) e retas
ı ı ¸˜
geratrizes paralelas ao vetor V = ( a, b, 1) e
´
f ( x − az, y − bz) = 0.
Resultados an´ logos s˜ o obtidos se a curva diretriz est´ situada nos planos coorde-
a a a
nados yz e xz.
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

413. 6.2 ı ı o ¸˜
Superf´cies Cil´ndricas, Cˆ nicas e de Revolucao 401
z
V P
P
x
y
Figura 6.30 – Superf´cie cil´ndrica
ı ı
Marco 2012
¸ Reginaldo J. Santos

414. 402 Superf´cies e Curvas no Espaco
ı ¸
¸˜
Proposicao 6.1. Considere uma superf´cie cil´ndrica.
ı ı
(a) Se a sua curva diretriz est´ no plano xy com equa¸ ao neste plano dada por
a c˜
f ( x, y) = 0
e as retas geratrizes s˜ o paralelas ao vetor V = ( a, b, 1), ent˜ o a sua equa¸ ao e
a a c˜ ´
f ( x − az, y − bz) = 0.
(b) Se a sua curva diretriz est´ no plano yz com equa¸ ao neste plano dada por
a c˜
f (y, z) = 0
e as retas geratrizes s˜ o paralelas ao vetor V = (1, b, c), ent˜ o a sua equa¸ ao e
a a c˜ ´
f (y − bx, z − cx ) = 0.
(c) Se a sua curva diretriz est´ no plano xz com equa¸ ao neste plano dada por
a c˜
f ( x, z) = 0
e as retas geratrizes s˜ o paralelas ao vetor V = ( a, 1, c), ent˜ o a sua equa¸ ao e
a a c˜ ´
f ( x − ay, z − cy) = 0.
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

415. 6.2 ı ı o ¸˜
Superf´cies Cil´ndricas, Cˆ nicas e de Revolucao 403
z
x y
Figura 6.31 – Superf´cie cil´ndrica com diretrizes paralelas ao vetor W = (1, −2, 3) e curva geratriz x2 − 4y = 0,
ı ı
z=0
Marco 2012
¸ Reginaldo J. Santos

416. 404 Superf´cies e Curvas no Espaco
ı ¸
Exemplo 6.1. Vamos determinar a equacao da superf´cie cil´ndrica que tem como
¸˜ ı ı
curva diretriz no plano xy a par´ bola de equacao x2 − 4y = 0 e retas diretrizes pa-
a ¸˜
ralelas ao vetor W = (1, −2, 3). Para obtermos um vetor que tem a 3a componente
igual a 1 multiplicamos o vetor W por 1/3 obtendo o vetor V = (1/3, −2/3, 1) que
e ´ ` ¸˜ ı ´
tamb´ m e paralelo as retas geratrizes. A equacao da superf´cie e ent˜ o
a
( x − z/3)2 − 4(y + 2z/3) = 0.
¸˜
Consideremos o problema inverso, ou seja, uma superf´cie de equacao
ı
F ( x, y, z) = 0
´
e uma superf´cie cil´ndrica se puder ser escrita na forma
ı ı
f ( x − az, y − bz) = 0 ou f (y − bx, z − cx ) = 0 ou f ( x − ay, z − cy) = 0.
Exemplo 6.2. Vamos mostrar que a superf´cie de equacao
ı ¸˜
−3x2 + 3y2 + 2xz + 4yz + z2 = 27
e uma superf´cie cil´ndrica. Fazendo z = 0 obtemos a curva candidata a diretriz no
´ ı ı
plano xy
−3x2 + 3y2 = 27
Agora, substituindo-se x por x − αz e y por y − βz na equacao da candidata a curva
¸˜
diretriz obtemos
−3( x − αz)2 + 3(y − βz)2 = −3x2 + 3y2 + 6αxz − 6βyz + (−3α2 + 3β2 )z2 = 27.
¸˜
Comparando-se com a equacao da superf´cie obtemos que
ı
α = 1/3 e β = −2/3
Portanto a superf´cie e cil´ndrica com retas geratrizes paralelas ao vetor V =
ı ´ ı
(1/3, −2/3, 1) e com curva diretriz −3x2 + 3y2 = 27.
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

417. 6.2 ı ı o ¸˜
Superf´cies Cil´ndricas, Cˆ nicas e de Revolucao 405
z
x y
Figura 6.32 – Superf´cie cil´ndrica de equacao −3x2 + 3y2 + 2xz + 4yz + z2 = 27
ı ı ¸˜
Marco 2012
¸ Reginaldo J. Santos

418. 406 Superf´cies e Curvas no Espaco
ı ¸
6.2.2 Superf´cies Cˆ nicas
ı o
ı ˆ ´
Uma superf´cie conica e uma superf´cie que pode ser obtida quando uma reta se
ı
move de maneira que sempre passa por uma curva fixa, chamada diretriz, e por um
ponto fixo, chamado v´ rtice, n˜ o situado no plano da geratriz.
e a
Suponhamos que a curva diretriz da superf´cie conica S esteja no plano z = c e tenha
ı ˆ
¸˜
equacao neste plano dada por
f ( x, y) = 0 (6.9)
e que o v´ rtice esteja na origem O = (0, 0, 0). Seja P = ( x, y, z) uma ponto qualquer
e
de S e P = ( x , y , c) o ponto da curva diretriz situado na reta que une P a origem.
`
−→ −→
O ponto P pertence a S se, e somente se, o vetor OP e paralelo a OP e P e um ponto
´ ´
da curva diretriz, ou seja,
−→ −→
OP= λ OP e f ( x , y ) = 0,
´
que e equivalente a
( x, y, z) = λ( x , y , c) e f ( x , y ) = 0.
Destas equacoes obtemos que λ = z/c, x = cx/z e y = cy/z. Assim a equacao da
¸˜ ¸˜
superf´cie conica S que tem curva diretriz no plano z = c com equacao (6.9) e v´ rtice
ı ˆ ¸˜ e
na origem e ´
cx cy
f ( , ) = 0.
z z
Resultados an´ logos s˜ o obtidos se a curva diretriz est´ situada nos planos y = b e
a a a
x = a.
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

419. 6.2 ı ı o ¸˜
Superf´cies Cil´ndricas, Cˆ nicas e de Revolucao 407
z
P
P
x
y
ˆ
Figura 6.33 – Superf´cie conica
ı
Marco 2012
¸ Reginaldo J. Santos

420. 408 Superf´cies e Curvas no Espaco
ı ¸
¸˜
Proposicao 6.2. Considere uma superf´cie cˆ nica.
ı o
(a) Se a sua curva diretriz est´ no plano z = c com equa¸ ao neste plano dada por
a c˜
f ( x, y) = 0
e o v´rtice est´ na origem, ent˜ o a sua equa¸ ao e
e a a c˜ ´
cx cy
f( , ) = 0.
z z
(b) Se a sua curva diretriz est´ no plano x = a com equa¸ ao neste plano dada por
a c˜
f (y, z) = 0
e o v´rtice est´ na origem, ent˜ o a sua equa¸ ao e
e a a c˜ ´
ay az
f( , ) = 0.
x x
(c) Se a sua curva diretriz est´ no plano y = b com equa¸ ao neste plano dada por
a c˜
f ( x, z) = 0
e o v´rtice est´ na origem, ent˜ o a sua equa¸ ao e
e a a c˜ ´
bx bz
f( , ) = 0.
y y
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

421. 6.2 ı ı o ¸˜
Superf´cies Cil´ndricas, Cˆ nicas e de Revolucao 409
z
y
x
Figura 6.34 – Superf´cie conica cuja curva diretriz e x2 − 2y = 0, z = 1.
ı ˆ ´
Marco 2012
¸ Reginaldo J. Santos

422. 410 Superf´cies e Curvas no Espaco
ı ¸
Exemplo 6.3. Considere a par´ bola situada no plano z = 1 de equacao
a ¸˜
x2 = 2y.
¸˜ ˆ ´
A equacao da superf´cie conica cuja curva diretriz e esta par´ bola e com v´ rtice na
ı a e
origem O = (0, 0, 0) e obtida trocando-se x por x/z e y por y/z na equacao acima.
´ ¸˜
Ou seja,
( x/z)2 = 2(y/z).
ou
x2 = 2yz.
¸˜
Consideremos o problema inverso, ou seja, uma superf´cie de equacao
ı
F ( x, y, z) = 0
e uma superf´cie conica com v´ rtice na origem O = (0, 0, 0) se sempre que um ponto
´ ı ˆ e
P = ( x, y, z) = (0, 0, 0) pertence a ela, ent˜ o a reta que passa pela origem e por P est´
a a
contida na superf´cie. Ou seja, se um ponto P = ( x, y, z) = (0, 0, 0) satisfaz a equacao
ı ¸˜
da superf´cie, ent˜ o o ponto P = (λx, λy, λz) tamb´ m satisfaz, para todo λ ∈ R.
ı a e
Exemplo 6.4. A superf´cie de equacao
ı ¸˜
4x2 − y2 + 4z2 = 0,
e uma superf´cie conica com v´ rtice na origem O = (0, 0, 0), pois se ( x, y, z) satisfaz a
´ ı ˆ e
equacao acima, ent˜ o tamb´ m (λx, λy, λz), para todo λ ∈ R. Fazendo z = 1 obtemos
¸˜ a e
a curva diretriz no plano z = 1 de equacao
¸˜
4x2 − y2 + 4 = 0,
´
que e uma hip´ rbole.
e
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

423. 6.2 ı ı o ¸˜
Superf´cies Cil´ndricas, Cˆ nicas e de Revolucao 411
z
y
x
Figura 6.35 – Superf´cie conica de equacao 4x2 − y2 + 4z2 = 0.
ı ˆ ¸˜
Marco 2012
¸ Reginaldo J. Santos

424. 412 Superf´cies e Curvas no Espaco
ı ¸
¸˜
6.2.3 Superf´cies de Revolucao
ı
c˜ ´ ¸˜
Uma superf´cie de revolu¸ ao e uma superf´cie que pode ser obtida pela rotacao de
ı ı
uma curva plana, chamada geratriz, em torno de uma reta fixa, chamada eixo (de
revolu¸ ao), no plano da referida curva. Cada ponto em cima da geratriz descreve
c˜
e e ´
uma circunferˆ ncia em torno do eixo. Esta circunferˆ ncia e chamada paralelo da
¸˜ ´
superf´cie e cada posicao da curva geratriz e chamada se¸ ao meridiana.
ı c˜
¸˜ ´
Se o eixo de revolucao e o eixo z e uma curva geratriz que est´ situada no plano yz
a
¸˜
tem equacao neste plano dada por
f (y, z) = 0, (6.10)
ent˜ o o paralelo que tem altura igual a z e uma circunferˆ ncia de raio dado por
a ´ e
r = x2 + y2 . Por outro lado, um dos pares (r, z) ou (−r, z) satisfaz a equacao¸˜
(6.10), pois o paralelo intercepta o plano yz nos pontos P = (0, r, z) e P = (0, −r, z).
Assim o ponto P = ( x, y, z) satisfaz a equacao
¸˜
f( x 2 + y2 , z ) = 0 ou f (− x2 + y2 , z) = 0. (6.11)
¸˜
Se uma curva geratriz que est´ situada no plano xz tem equacao neste plano dada
a
por
f ( x, z) = 0, (6.12)
ent˜ o o paralelo que tem altura igual a z e uma circunferˆ ncia de raio dado por
a ´ e
r = x 2 + y2 . Por outro lado, um dos pares (r, z ) ou (−r, z ) satisfaz a equacao
¸˜
(6.12), pois o paralelo intercepta o plano xz nos pontos (r, 0, z) e (−r, 0, z). Assim o
ponto ( x, y, z) satisfaz a equacao
¸˜
f( x 2 + y2 , z ) = 0 ou f (− x2 + y2 , z) = 0. (6.13)
a a ¸˜ ´
Resultados an´ logos s˜ o obtidos quando o eixo de revolucao e o eixo x e o eixo y.
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

425. 6.2 ı ı o ¸˜
Superf´cies Cil´ndricas, Cˆ nicas e de Revolucao 413
z
P P
x
y
¸˜
Figura 6.36 – Superf´cie de revolucao em torno do eixo z
ı
Marco 2012
¸ Reginaldo J. Santos

426. 414 Superf´cies e Curvas no Espaco
ı ¸
¸˜
Proposicao 6.3. Considere uma superf´cie de revolu¸ ao.
ı c˜
(a) Se o seu eixo de revolu¸ ao e o eixo x e a curva geratriz est´ situada no plano xz com equa¸ ao neste plano dada por
c˜ ´ a c˜
f ( x, z) = 0, ent˜ o a equa¸ ao da superf´cie e
a c˜ ı ´
f ( x, ± y2 + z2 ) = 0.
Se a curva geratriz est´ situada no plano xy com equa¸ ao neste plano dada por f ( x, y) = 0, ent˜ o a equa¸ ao da
a c˜ a c˜
superf´cie e
ı ´
f ( x, ± y2 + z2 ) = 0.
(b) Se o seu eixo de revolu¸ ao e o eixo y e a curva geratriz est´ situada no plano yz com equa¸ ao neste plano dada por
c˜ ´ a c˜
f (y, z) = 0, ent˜ o a equa¸ ao da superf´cie e
a c˜ ı ´
f (y, ± x2 + z2 ) = 0.
Se a curva geratriz est´ situada no plano xy com equa¸ ao neste plano dada por f ( x, y) = 0, ent˜ o a equa¸ ao da
a c˜ a c˜
superf´cie e
ı ´
f (± x2 + z2 , y) = 0.
(c) Se o seu eixo de revolu¸ ao e o eixo z e a curva geratriz est´ situada no plano yz com equa¸ ao neste plano dada por
c˜ ´ a c˜
f (y, z) = 0, ent˜ o a equa¸ ao da superf´cie e
a c˜ ı ´
f (± x2 + y2 , z) = 0.
Se a curva geratriz est´ situada no plano xz com equa¸ ao neste plano dada por f ( x, z) = 0, ent˜ o a equa¸ ao da
a c˜ a c˜
superf´cie e
ı ´
f (± x2 + y2 , z) = 0.
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

427. 6.2 ı ı o ¸˜
Superf´cies Cil´ndricas, Cˆ nicas e de Revolucao 415
Exemplo 6.5. (a) Considere a elipse situada no plano xz de equacao neste plano
¸˜
dada por
x2 z2
+ 2 = 1.
a2 b
¸˜ ¸˜ ¸˜
A equacao da superf´cie de revolucao gerada pela rotacao desta elipse em torno
ı
do eixo z e obtida trocando-se x por ± x
´ 2 + y2 na equacao acima. Ou seja,
¸˜
x2 y2 z2
2
+ 2 + 2 = 1,
a a b
´ ¸˜
que e a equacao de um elipsoide.
¸˜
(b) Considere a hip´ rbole situada no plano xz de equacao neste plano dada por
e
x2 z2
− 2 = 1.
a2 b
¸˜ ¸˜ ¸˜
A equacao da superf´cie de revolucao gerada pela rotacao desta hip´ rbole em
ı e
torno do eixo z e obtida trocando-se x por ± x
´ 2 + y2 na equacao acima. Ou
¸˜
seja,
x2 y2 z2
+ 2 − 2 = 1,
a2 a b
´ ¸˜
que e a equacao de um hiperboloide de uma folha.
¸˜
(c) Considere a hip´ rbole situada no plano xy de equacao neste plano dada por
e
y2 x2
2
− 2 = 1.
a b
Marco 2012
¸ Reginaldo J. Santos

428. 416 Superf´cies e Curvas no Espaco
ı ¸
z
x y
¸˜
Figura 6.37 – Elipsoide de revolucao em torno do eixo z
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

429. 6.2 ı ı o ¸˜
Superf´cies Cil´ndricas, Cˆ nicas e de Revolucao 417
z
x y
¸˜
Figura 6.38 – Hiperboloide de uma folha de revolucao em torno do eixo z
Marco 2012
¸ Reginaldo J. Santos

430. 418 Superf´cies e Curvas no Espaco
ı ¸
¸˜ ¸˜
A equacao da superf´cie de revolucao gerada √
ı ¸˜
pela rotacao desta hip´ rbole em
e
torno do eixo y e obtida trocando-se x por ± x
´ 2 + z2 na equacao acima. Ou
¸˜
seja,
y2 x2 z2
− 2 − 2 = 1,
a2 b b
´ ¸˜
que e a equacao de um hiperboloide de duas folhas.
¸˜
(d) Considere a par´ bola situada no plano xz de equacao neste plano dada por
a
x2
z=
a2
¸˜ ¸˜ ¸˜
A equacao da superf´cie de revolucao gerada pela rotacao desta par´ bola em
ı a
torno do eixo z e obtida trocando-se x por ± x2 + y2 na equacao acima. Ou
´ ¸˜
seja,
x2 y2
z = 2 + 2,
a a
´ ¸˜
que e a equacao de um paraboloide el´ptico.
ı
¸˜
(e) Considere a reta situada no plano xz de equacao neste plano dada por
x
z= .
a
¸˜ ¸˜ ¸˜
A equacao da superf´cie de revolucao gerada pela rotacao desta reta em torno
ı
do eixo z e obtida trocando-se x por ± x2 + y2 na equacao acima. Ou seja,
´ ¸˜
± x 2 + y2
z=
a
´ ` ¸˜
que e equivalente a equacao
x2 y2
z2 = 2
+ 2,
a a
´ ¸˜
que e a equacao de um cone circular.
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

431. 6.2 ı ı o ¸˜
Superf´cies Cil´ndricas, Cˆ nicas e de Revolucao 419
z
y
x
¸˜
Figura 6.39 – Hiperboloide de duas folhas de revolucao em torno do eixo y
Marco 2012
¸ Reginaldo J. Santos

432. 420 Superf´cies e Curvas no Espaco
ı ¸
z
x y
¸˜
Figura 6.40 – Paraboloide el´ptico de revolucao em torno do eixo z
ı
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

433. 6.2 ı ı o ¸˜
Superf´cies Cil´ndricas, Cˆ nicas e de Revolucao 421
z
x
y
¸˜
Figura 6.41 – Cone el´ptico de revolucao em torno do eixo z
ı
Marco 2012
¸ Reginaldo J. Santos

434. 422 Superf´cies e Curvas no Espaco
ı ¸
¸˜
Consideremos o problema inverso, ou seja, uma superf´cie de equacao
ı
F ( x, y, z) = 0
´ ¸˜
e uma superf´cie de revolucao em torno de um dos eixos coordenados se as in-
ı
˜
tercessoes da superf´cie com planos perpendiculares ao referido eixo s˜ o circun-
ı a
ferˆ ncias com centros no referido eixo.
e
Exemplo 6.6. A superf´cie de equacao
ı ¸˜
x2 + y2 = (cos(πz) − 3/2)2
e de uma superf´cie de revolucao, pois fazendo z = k obtemos a equacao de uma
´ ı ¸˜ ¸˜
circunferˆ ncia neste plano
e
x2 + y2 = (cos(πk) − 3/2)2
Exemplo 6.7. (a) Um elipsoide que tem dois dos seus parˆ metros iguais e um elip-
a ´
¸˜
soide de revolucao. Por exemplo,
x2 y2 z2
+ 2 + 2 = 1,
a2 a c
x2 y2 z2
+ 2 + 2 = 1,
a2 b b
x2 y2 z2
2
+ 2 + 2 = 1,
a b a
¸˜ ¸˜
s˜ o equacoes de elipsoides de revolucao. O primeiro, em torno do eixo z, o
a
segundo, em torno do eixo x e o terceiro, em torno do eixo y.
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

435. 6.2 ı ı o ¸˜
Superf´cies Cil´ndricas, Cˆ nicas e de Revolucao 423
z
x
y
Figura 6.42 – Superf´cie de revolucao em torno do eixo z de equacao x2 + y2 = (cos(πz) − 3/2)2
ı ¸˜ ¸˜
Marco 2012
¸ Reginaldo J. Santos

436. 424 Superf´cies e Curvas no Espaco
ı ¸
(b) O hiperboloide de uma folha que tem os parˆ metros iguais associados aos ter-
a
´ ¸˜
mos de sinal positivo e um hiperboloide uma folha de revolucao. Por exemplo,
x2 y2 z2
+ 2 − 2 = 1,
a2 a c
x2 y2 z2
− + 2 + 2 = 1,
a2 b b
x2 y2 z2
2
− 2 + 2 = 1,
a b a
¸˜ ¸˜
s˜ o equacoes de hiperboloides de uma folha de revolucao. O primeiro, em torno
a
do eixo z, o segundo, em torno do eixo x e o terceiro, em torno do eixo y.
(c) O hiperboloide de duas folhas que tem os parˆ metros iguais associados aos ter-
a
´ ¸˜
mos de sinal negativo e um hiperboloide duas folhas de revolucao. Por exem-
plo,
x2 y2 z2
− 2 − 2 + 2 = 1,
a a c
x2 y2 z2
− 2 − 2 = 1,
a2 b b
x2 y2 z2
−
+ 2 − 2 = 1,
a2 b a
¸˜ ¸˜
s˜ o equacoes de hiperboloides de duas folhas de revolucao. O primeiro, em
a
torno do eixo z, o segundo, em torno do eixo x e o terceiro, em torno do eixo y.
¸˜
(d) O cone circular de equacao
x2 y2
z2 =
+ 2,
a2 a
x
pode ser obtido pela rotacao da reta situada no plano xz de equacao z =
¸˜ ¸˜ a em
torno do eixo z.
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

437. 6.2 ı ı o ¸˜
Superf´cies Cil´ndricas, Cˆ nicas e de Revolucao 425
Exerc´cios Num´ ricos
ı e
¸˜ ` ¸˜
6.2.1. Dadas as equacoes da curva diretriz e um vetor paralelo as retas geratrizes determine a equacao da
superf´cie cil´ndrica
ı ı
(a) y2 = 4x, z = 0 e V = (1, −1, 1) (c) x2 − y2 = 1, z = 0 e V = (0, 2, −1)
(b) x 2 + z2 = 1, y = 0 e V = (2, 1, −1) (d) 4x2 + z2 + 4z = 0, y = 0 e V = (4, 1, 0)
¸˜ ¸˜
6.2.2. Mostre que cada uma das equacoes representa uma superf´cie cil´ndrica e determine a equacao da curva
ı ı
`
diretriz e um vetor paralelo as retas geratrizes
(a) x2 + y2 + 2z2 + 2xz − 2yz = 1 (c) 17x2 + 2y2 + z2 − 8xy − 6xz − 2 = 0
(b) x2 + y + 5z2 + 2xz + 4yz − 4 = 0 (d) xz + 2yz − 1 = 0
¸˜ ¸˜ ˆ
6.2.3. Dadas as equacoes da curva diretriz determine a equacao da superf´cie conica que tem v´ rtice na origem
ı e
O = (0, 0, 0).
(a) x2 + y2 = 4 e z = 2 (c) y = x2 e z = 2
(b) xz = 1 e y = 1 (d) x2 − 4z2 = 4 e y = 3
6.2.4. Mostre que cada uma das equacoes representa uma superf´cie conica com v´ rtice na origem O = (0, 0, 0)
¸˜ ı ˆ e
¸˜
e determine a equacao de uma curva diretriz
(a) x2 − 2y2 + 4z2 = 0 (c) 8y4 − yz3 = 0
(b) 4z3 − x2 y = 0 (d) xy + xz + yz = 0
¸˜ ¸˜ ¸˜
6.2.5. Determine a equacao da superf´cie de revolucao gerada pela rotacao da curva dada em torno do eixo
ı
especificado.
(a) 9x2 + 4y2 = 36 e z = 0 em torno do eixo y (c) yz = 1 e x = 0 em torno do eixo z
(b) x 2 − 2z2 + 4z = 6 e y = 0 em torno do eixo x (d) z = e x e y = 0 em torno do eixo z
¸˜ ¸˜
6.2.6. Mostre que cada uma das equacoes representa uma superf´cie de revolucao e determine o seu eixo de
ı
¸˜ ¸˜
revolucao e a equacao de uma curva geratriz
(a) x2 + y2 − z3 = 0 (c) y6 − x2 − z2 = 0
(b) x2 + z2 = 4 (d) x2 y2 + x2 z2 = 1
Marco 2012
¸ Reginaldo J. Santos

438. 426 Superf´cies e Curvas no Espaco
ı ¸
Exerc´cios Teoricos
ı ´
¸˜
6.2.7. Mostre que conjunto dos pontos do espaco que satisfazem uma equacao da forma
¸
f ( x, y) = 0 ou f ( x, z) = 0 ou f (y, z) = 0
representa uma superf´cie cil´ndrica que tem retas geratrizes paralelas ao eixo cuja vari´ vel n˜ o aparece
ı ı a a
¸˜ ¸˜ ´ ¸˜
na equacao. Equacao esta que e tamb´ m a equacao da curva diretriz no plano coordenado correspon-
e
` ¸˜
dente as vari´ veis que aparecem na equacao.
a
6.2.8. Mostre que a equacao de uma superf´cie conica com v´ rtice num ponto P0 = ( x0 , y0 , z0 ) e curva diretriz
¸˜ ı ˆ e
situada no plano z = c com equacao f ( x, y) = 0 e
¸˜ ´
c − z0 c − z0
f x0 + ( x − x0 ), y0 + ( y − y0 ) = 0.
z − z0 z − z0
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

439. 6.3 ı e ¸˜
Coordenadas Cil´ndricas, Esf´ ricas e Equacoes Param´ tricas
e 427
6.3 ı e ¸˜
Coordenadas Cil´ndricas, Esf´ ricas e Equacoes Param´ tricas
e
6.3.1 Coordenadas Cil´ndricas
ı
At´ agora vimos usando o chamado sistema de coordenadas cartesianas, em que
e
¸ ´ ¸˜
um ponto no espaco e localizado em relacao a trˆ s retas fixas perpendiculares entre
e
si. Vamos definir um outro sistema de coordenadas chamado de sistema de coorde-
¸ ´ ¸˜
nadas cil´ndricas em que um ponto do espaco e localizado em relacao a duas retas
ı
(usualmente o eixo z e o eixo x do sistema cartesiano) e um ponto (usualmente a
origem O do sistema cartesiano).
¸ ´
No sistema de coordenadas cil´ndricas um ponto no espaco e localizado da seguinte
ı
forma. Passa-se por P uma reta paralela ao eixo z. Seja P o ponto em que esta reta
intercepta o plano xy. Sejam (r, θ ) as coordenadas polares de P no plano xy. As
coordenadas cil´ndricas do ponto P s˜ o as coordenadas polares de P juntamente
ı a
com a terceira coordenada retangular, z, de P e s˜ o escritas na forma (r, θ, z).
a
¸˜
Segue facilmente as relacoes entre as coordenadas cartesianas e as coordenadas
cil´ndricas.
ı
¸˜
Proposicao 6.4. Suponha que o polo e o eixo polar do sistema de coordenadas polares no plano xy coincidem com a
origem e o eixo x do sistema de coordenadas cartesianas no plano xy, respectivamente. Ent˜ o a transforma¸ ao entre os
a c˜
sistemas de coordenadas cil´ndricas e o de coordenadas cartesianas podem ser realizadas pelas equa¸ oes
ı c˜
x = r cos θ e y = r sen θ
r= x 2 + y2 ,
x y
cos θ = e sen θ = , se x2 + y2 = 0
x2 + y2 x2 + y2
Marco 2012
¸ Reginaldo J. Santos

440. 428 Superf´cies e Curvas no Espaco
ı ¸
z
z
P
z
y
x θ r
P y
x
Figura 6.43 – Coordenadas cil´ndricas e cartesianas de um ponto P no espaco
ı ¸
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

441. 6.3 ı e ¸˜
Coordenadas Cil´ndricas, Esf´ ricas e Equacoes Param´ tricas
e 429
Exemplo 6.8. Vamos determinar a equacao em coordenadas cil´ndricas do parabo-
¸˜ ı
¸˜
loide el´ptico de equacao
ı
x2 + y2 = a2 z.
Substituindo x por r cos θ e y por sen θ obtemos
r2 = a2 z.
Exemplo 6.9. Vamos determinar a equacao em coordenadas cil´ndricas do parabo-
¸˜ ı
´ ¸˜
loide hiperbolico de equacao
y2 − x2 = a2 z.
Substituindo x por r cos θ e y por r sen θ obtemos
−r2 cos 2θ = a2 z.
Exemplo 6.10. Vamos determinar a equacao em coordenadas cartesianas da su-
¸˜
¸˜ ´
perf´cie cuja equacao em coordenadas cil´ndricas e
ı ı
r = a sen θ.
Multiplicando-se ambos os membros da equacao por r obtemos
¸˜
r2 = ar sen θ.
Como r2 = x2 + y2 e r sen θ = y, ent˜ o obtemos
a
x2 + y2 = ay,
´ ¸˜ ¸˜
que e a equacao de um cilindro gerado pela circunferˆ ncia no plano xy de equacao
e
em coordenadas polares e r = a sen θ, ou seja, uma circunferˆ ncia com raio a/2 e
´ e
centro no ponto cujas coordenadas cartesianas s˜ o (0, a/2).
a
Marco 2012
¸ Reginaldo J. Santos

442. 430 Superf´cies e Curvas no Espaco
ı ¸
z
x y
Figura 6.44 – Paraboloide el´ptico de equacao em coordenadas cil´ndricas r2 = a2 z
ı ¸˜ ı
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

443. 6.3 ı e ¸˜
Coordenadas Cil´ndricas, Esf´ ricas e Equacoes Param´ tricas
e 431
z
y
x
Figura 6.45 – Paraboloide hiperbolico de equacao em coordenadas cil´ndricas r2 cos 2θ = − a2 z
´ ¸˜ ı
Marco 2012
¸ Reginaldo J. Santos

444. 432 Superf´cies e Curvas no Espaco
ı ¸
z
x y
Figura 6.46 – Cilindro circular de equacao em coordenadas cil´ndricas r = a sen θ
¸˜ ı
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

445. 6.3 ı e ¸˜
Coordenadas Cil´ndricas, Esf´ ricas e Equacoes Param´ tricas
e 433
z
z
P
r
φ
y
x
θ
P y
x
Figura 6.47 – Coordenadas esf´ ricas e cartesianas de um ponto P no espaco
e ¸
Marco 2012
¸ Reginaldo J. Santos

446. 434 Superf´cies e Curvas no Espaco
ı ¸
6.3.2 Coordenadas Esf´ ricas
e
Vamos definir um outro sistema de coordenadas chamado de sistema de coorde-
¸ ´ ¸˜
nadas esf´ ricas em que um ponto do espaco e localizado em relacao a duas retas
e
(usualmente o eixo z e o eixo x do sistema cartesiano) e um ponto (usualmente a
origem O do sistema cartesiano).
¸ ´
No sistema de coordenadas esf´ ricas um ponto no espaco e localizado da seguinte
e
forma. Passa-se por P uma reta paralela ao eixo z. Seja P o ponto em que esta reta
intercepta o plano xy. Seja θ a segunda coordenada polar de P no plano xy. As
coordenadas esf´ ricas do ponto P s˜ o a distˆ ncia de P a origem, r = dist( P, O), o
e a a `
−→
angulo, φ, entre os vetores OP e k = (0, 0, 1) e a segunda coordenada polar de P , θ.
ˆ
As coordenadas esf´ ricas de um ponto P s˜ o escritas na forma (r, φ, θ ).
e a
¸˜
Segue facilmente as relacoes entre as coordenadas cartesianas e as coordenadas
esf´ ricas.
e
¸˜
Proposicao 6.5. Suponha que o polo e o eixo polar do sistema de coordenadas polares no plano xy coincidem com a
origem e o eixo x do sistema de coordenadas cartesianas no plano xy, respectivamente. Ent˜ o a transforma¸ ao entre os
a c˜
sistemas de coordenadas esf´ricas e o de coordenadas cartesianas podem ser realizadas pelas equa¸ oes
e c˜
x = r sen φ cos θ, y = r sen φ sen θ e z = r cos φ
x 2 + y2 π
r= x 2 + y2 + z2 , tan φ = , se z = 0, φ = , se z = 0,
z 2
x y
cos θ = e sen θ = , se x2 + y2 = 0.
x2 + y2 x 2 + y2
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

447. 6.3 ı e ¸˜
Coordenadas Cil´ndricas, Esf´ ricas e Equacoes Param´ tricas
e 435
Exemplo 6.11. Vamos determinar a equacao em coordenadas esf´ ricas do parabo-
¸˜ e
¸˜
loide el´ptico de equacao
ı
x2 + y2 = a2 z.
Substituindo x por r sen φ cos θ, y por r sen φ sen θ e z por r cos φ e dividindo por r
obtemos
r sen2 φ = a2 cos φ.
Exemplo 6.12. Vamos determinar a equacao em coordenadas esf´ ricas do parabo-
¸˜ e
´ ¸˜
loide hiperbolico de equacao
x2 − y2 = a2 z.
Substituindo x por r sen φ cos θ, y por r sen φ sen θ e z por r cos φ e dividindo por r
obtemos
r sen2 φ cos 2θ = a2 cos φ.
Exemplo 6.13. Vamos determinar a equacao em coordenadas cartesianas da su-
¸˜
¸˜ ´
perf´cie cuja equacao em coordenadas esf´ ricas e
ı e
r sen φ = a.
¸˜
Elevando-se ao quadrado a equacao acima obtemos
r2 sen2 φ = a2 .
Substituindo-se sen2 φ por 1 − cos2 φ obtemos
r2 − r2 cos2 φ = a2 .
Como r2 = x2 + y2 + z2 e r cos φ = z, ent˜ o obtemos
a
x 2 + y2 = a2 ,
´ ¸˜
que e a equacao de um cilindro circular.
Marco 2012
¸ Reginaldo J. Santos

448. 436 Superf´cies e Curvas no Espaco
ı ¸
z
x y
Figura 6.48 – Paraboloide el´ptico de equacao em coordenadas esf´ ricas r sen2 φ = a2 cos φ
ı ¸˜ e
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

449. 6.3 ı e ¸˜
Coordenadas Cil´ndricas, Esf´ ricas e Equacoes Param´ tricas
e 437
z
y
x
Figura 6.49 – Paraboloide hiperbolico de equacao em coordenadas esf´ ricas r sen2 φ cos 2θ = a2 cos φ
´ ¸˜ e
Marco 2012
¸ Reginaldo J. Santos

450. 438 Superf´cies e Curvas no Espaco
ı ¸
z
x y
Figura 6.50 – Cilindro circular de equacao em coordenadas esf´ ricas r sen φ = a
¸˜ e
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

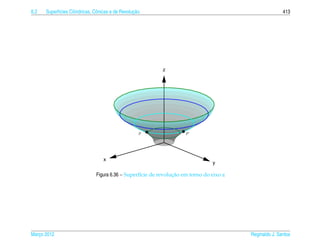
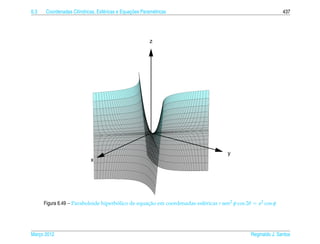
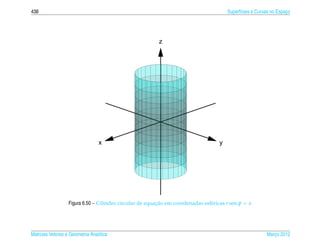
451. 6.3 ı e ¸˜
Coordenadas Cil´ndricas, Esf´ ricas e Equacoes Param´ tricas
e 439
¸˜
6.3.3 Equacoes Param´ tricas de Superf´cies
e ı
Seja
F ( x, y, z) = 0 (6.14)
a equacao de uma superf´cie S em coordenadas retangulares. Sejam x, y e z funcoes
¸˜ ı ¸˜
de um par de vari´ veis (s, t) numa regi˜ o, R, do plano, ou seja,
a a
x = f (s, t), y = g(s, t) e z = h(s, t), para todo (s, t) ∈ R. (6.15)
Se para quaisquer (s, t) ∈ R, os valores de x, y e z determinados pelas equacoes (6.15)
¸˜
¸˜
satisfazem (6.14), ent˜ o as equacoes (6.15) s˜ o chamadas equa¸ oes param´ tricas da
a a c˜ e
superf´cie S e as vari´ veis independentes s e t s˜ o chamadas parˆ metros. Dize-
ı a a a
e ¸˜
mos tamb´ m que as equacoes (6.15) formam uma representa¸ ao param´ trica da su-
c˜ e
perf´cie S .
ı
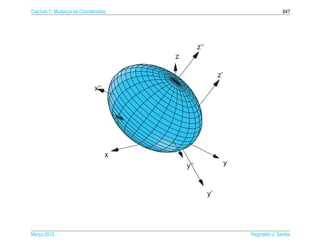
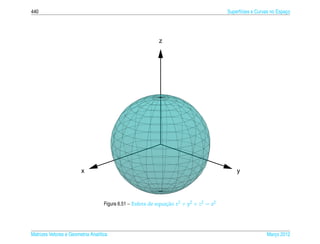
Exemplo 6.14. Seja a um numero real positivo fixo. A esfera de equacao
´ ¸˜
x 2 + y2 + z2 = a2 (6.16)
¸˜
pode ser representada parametricamente pelas equacoes
x = a sen s cos t, y = a sen s sen t e z = a cos s (6.17)
para todo s ∈ [0, π ] e para todo t ∈ [0, 2π ]. Pois elevando ao quadrado cada uma das
¸˜
equacoes (6.17) e somando os resultados obtemos
x 2 + y2 + z2 = a2 sen2 s cos2 t + a2 sen2 s sen2 t + a2 cos2 s
= a2 sen2 s(cos2 t + sen2 t) + a2 cos2 s = a2 .
A esfera definida por (6.16) pode tamb´ m ser representada parametricamente por
e
x = s, y=t e z= a2 − s2 − t2 , (6.18)
Marco 2012
¸ Reginaldo J. Santos

452. 440 Superf´cies e Curvas no Espaco
ı ¸
z
x y
Figura 6.51 – Esfera de equacao x2 + y2 + z2 = a2
¸˜
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

453. 6.3 ı e ¸˜
Coordenadas Cil´ndricas, Esf´ ricas e Equacoes Param´ tricas
e 441
para todo par (s, t) pertencente ao c´rculo de raio a. Ou ainda por
ı
x = s, y=t e z=− a2 − s2 − t2 , (6.19)
para todo par (s, t) pertencente ao c´rculo de raio a. Apenas que com (6.18) obtemos
ı
somente a parte de cima da esfera e com (6.19) obtemos somente a parte de baixo.
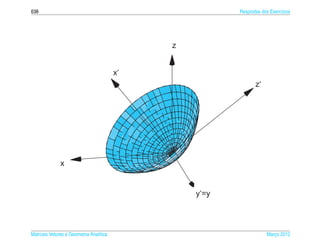
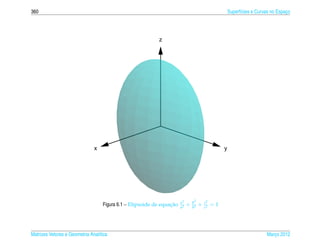
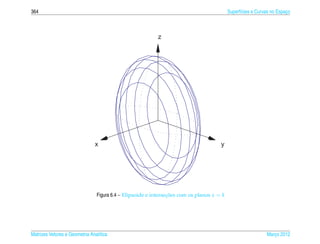
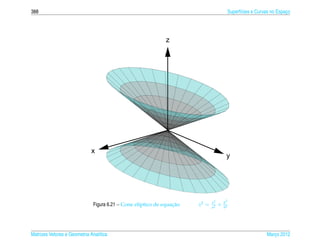
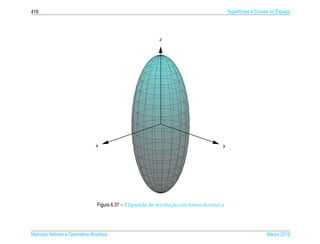
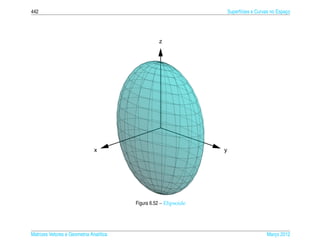
Exemplo 6.15. O elipsoide de equacao
¸˜
x2 y2 z2
2
+ 2 + 2 =1 (6.20)
a b c
¸˜
pode ser representada parametricamente pelas equacoes
x = a sen s cos t, y = b sen s sen t e z = c cos s (6.21)
para todo s ∈ [0, π ] e para todo t ∈ [0, 2π ]. Pois elevando ao quadrado e divi-
dindo por a2 a primeira equacao em (6.21), elevando ao quadrado e dividindo por
¸˜
b2 a segunda equacao em (6.21), elevando ao quadrado e dividindo por b2 a terceira
¸˜
¸˜
equacao em (6.21) e somando os resultados obtemos
x2 y2 z2
+ 2+ 2 = sen2 s cos2 t + sen2 s sen2 t + cos2 s
a2 b c
= sen2 s(cos2 t + sen2 t) + cos2 s = 1.
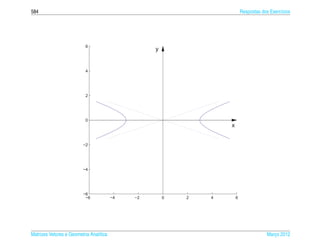
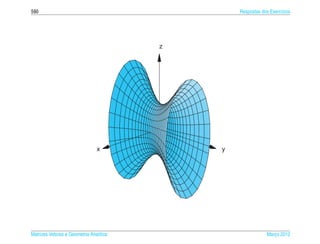
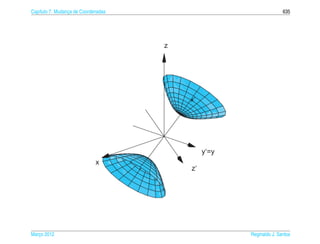
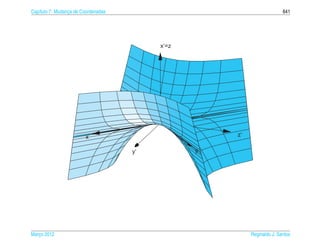
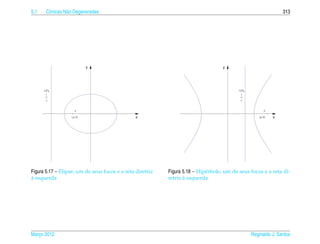
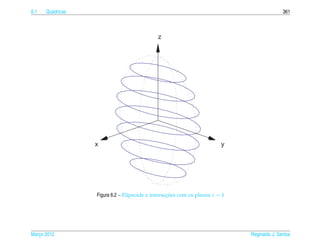
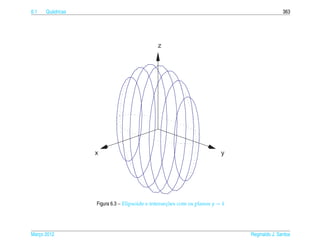
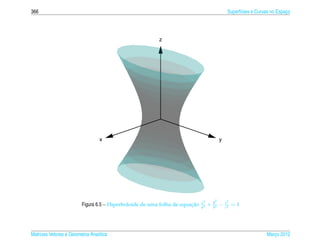
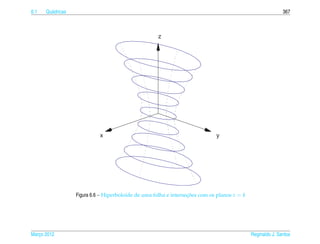
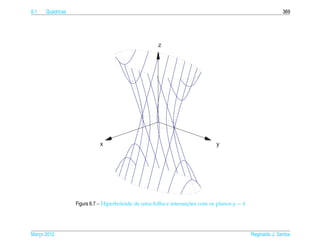
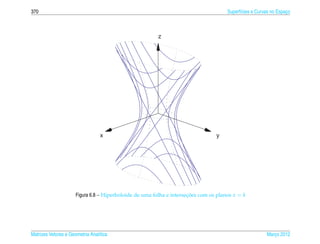
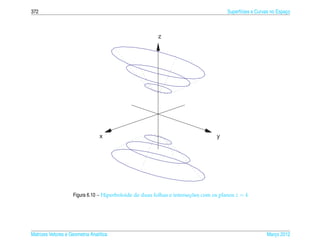
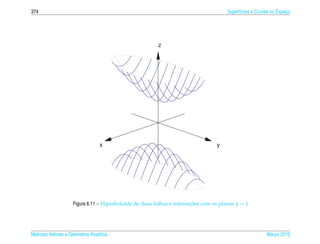
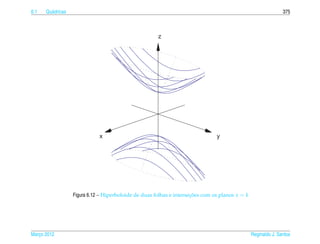
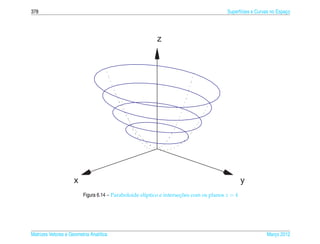
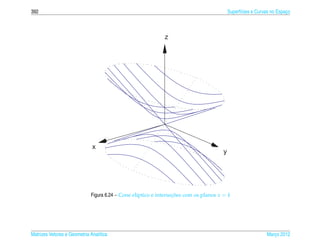
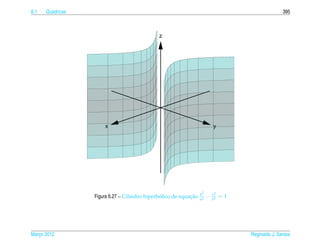
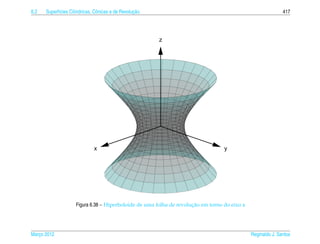
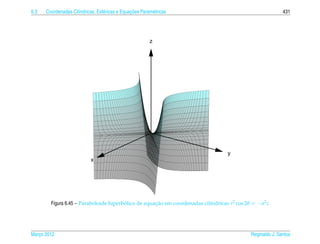
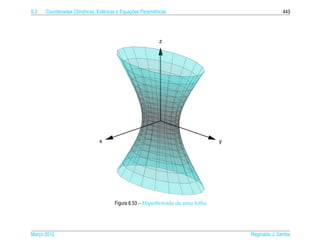
Exemplo 6.16. O hiperboloide de uma folha de equacao
¸˜
x2 y2 z2
+ 2 − 2 =1 (6.22)
a2 b c
¸˜
pode ser representado parametricamente pelas equacoes
x = a sec s cos t, y = b sec s sen t e z = c tan s, (6.23)
Marco 2012
¸ Reginaldo J. Santos

454. 442 Superf´cies e Curvas no Espaco
ı ¸
z
x y
Figura 6.52 – Elipsoide
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

455. 6.3 ı e ¸˜
Coordenadas Cil´ndricas, Esf´ ricas e Equacoes Param´ tricas
e 443
z
x y
Figura 6.53 – Hiperboloide de uma folha
Marco 2012
¸ Reginaldo J. Santos

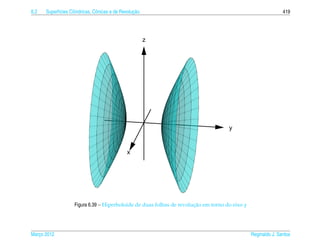
456. 444 Superf´cies e Curvas no Espaco
ı ¸
para todo s ∈ [0, 2π ], s = π/2, 3π/2 e para todo t ∈ [0, 2π ]. Pois elevando ao
quadrado e dividindo por a2 a primeira equacao em (6.23), elevando ao quadrado e
¸˜
dividindo por b2 a segunda equacao em (6.23), somando os resultados e subtraindo
¸˜
do quadrado da terceira equacao em (6.23) dividida por c2 obtemos
¸˜
x2 y2 z2
+ 2− 2 = sec2 s cos2 t + sec2 s sen2 t − tan2 s
a2 b c
= sec2 s (cos2 t + sen2 t) − tan2 s = 1.
¸˜ ´
Usando as funcoes hiperbolicas, o hiperboloide de uma folha definido por (6.22)
pode, tamb´ m, ser representado parametricamente, por
e
x = a cosh s cos t, y = b cosh s sen t e z = c senh s, (6.24)
para todo s ∈ R e para todo t ∈ [0, 2π ]. Pois elevando ao quadrado e dividindo
por a2 a primeira equacao em (6.24), elevando ao quadrado e dividindo por b2 a
¸˜
¸˜
segunda equacao em (6.24), somando os resultados e subtraindo do quadrado da
terceira equacao em (6.24) dividida por c2 obtemos
¸˜
x2 y2 z2
+ 2− 2 = cosh2 s cos2 t + cosh2 s sen2 t − senh2 s
a2 b c
= cosh2 s (cos2 t + sen2 t) − senh2 s = 1.
Exemplo 6.17. O paraboloide el´ptico de equacao
ı ¸˜
x2 y2
z= + 2 (6.25)
a2 b
¸˜
pode ser representado parametricamente pelas equacoes
x = as cos t, y = bs sen t e z = s2 , (6.26)
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

457. 6.3 ı e ¸˜
Coordenadas Cil´ndricas, Esf´ ricas e Equacoes Param´ tricas
e 445
z
x y
Figura 6.54 – Paraboloide el´ptico
ı
Marco 2012
¸ Reginaldo J. Santos

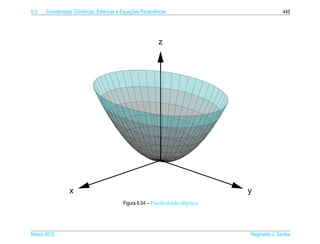
458. 446 Superf´cies e Curvas no Espaco
ı ¸
para todo s ∈ [0, +∞) e para todo t ∈ [0, 2π ]. Pois elevando ao quadrado e dividindo
por a2 a primeira equacao em (6.26), elevando ao quadrado e dividindo por b2 a
¸˜
¸˜
segunda equacao em (6.26), somando os resultados e subtraindo da terceira equacao ¸˜
em (6.26) obtemos
x2 y2
+ 2 −z = s2 cos2 t + s2 sen2 t − s2
a2 b
= s2 (cos2 t + sen2 t) − s2 = 0.
¸˜
6.3.4 Equacoes Param´ tricas de Curvas no Espaco
e ¸
a ¸˜
J´ estudamos a representacao param´ trica de uma curva no plano. Este conceito
e
pode ser estendido a curvas no espaco. Sejam x, y e z funcoes de uma vari´ vel t em
¸ ¸˜ a
um subconjunto, I , do conjunto dos numeros reais, R, ou seja,
´
x = f ( t ), y = g(t) e z = h ( t ), para todo t ∈ I . (6.27)
Quando t assume todos os valores em I , o ponto P(t) = ( f (t), g(t), g(t)) =
f (t)i + g(t) j + h(t)k descreve uma curva C no espaco. As equacoes (6.27) s˜ o chama-
¸ ¸˜ a
das equa¸ oes param´ tricas de C . A representacao param´ trica de curvas no espaco
c˜ e ¸˜ e ¸
tamb´ m tem um papel importante no tracado de curvas pelo computador. J´ vimos
e ¸ a
¸˜
um exemplo de representacao param´ trica de curvas no espaco quando estudamos
e ¸
a reta no espaco. ¸
Exemplo 6.18. Considere a curva parametrizada por
x = a cos t, y = b sen t e z = c t, para todo t ∈ R.
Vamos eliminar t nas duas primeiras equacoes. Para isso elevamos ao quadrado as
¸˜
duas primeiras equacoes, dividimos a primeira por a2 , a segunda por b2 e somamos
¸˜
obtendo
x2 y2
2
+ 2 = 1.
a a
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

459. 6.3 ı e ¸˜
Coordenadas Cil´ndricas, Esf´ ricas e Equacoes Param´ tricas
e 447
a ı ´
Portanto a curva est´ contida em um cilindro el´ptico. Esta curva e chamada h´ lice.
e
Exemplo 6.19. Vamos determinar uma parametrizacao para a curva √
¸˜ obtida da
¸˜ ¸˜2 2
intersecao do cone de equacao x + y 2 = z com o plano y + z = 2. Uma
¸˜ ´
parametrizacao para o cone e
x = s cos t, y = s sen t e z = s.
Vamos usar a equacao do plano para eliminar s na parametrizacao do cone.
¸˜ ¸˜
¸˜ ¸˜
Substituindo-se a parametrizacao do cone na equacao do plano obtemos
√
s sen t + s = 2.
Assim, √
2
s= .
sen t + 1
Portanto, √ √ √
2 cos t 2 sen t 2
x= , y= e z=
sen t + 1 sen t + 1 sen t + 1
para t ∈ (−π/2, 3π/2) e uma parametrizacao para a curva.
´ ¸˜
Marco 2012
¸ Reginaldo J. Santos

460. 448 Superf´cies e Curvas no Espaco
ı ¸
z
x y
Figura 6.55 – H´ lice
e
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

461. 6.3 ı e ¸˜
Coordenadas Cil´ndricas, Esf´ ricas e Equacoes Param´ tricas
e 449
z
y
x
√
Figura 6.56 – Curva obtida pelo corte do cone x2 + y2 = z2 pelo plano y − z = 2
Marco 2012
¸ Reginaldo J. Santos

462. 450 Superf´cies e Curvas no Espaco
ı ¸
Exerc´cios Num´ ricos (respostas na p´ gina 598)
ı e a
¸˜ ¸˜
6.3.1. Encontre uma equacao em coordenadas cil´ndricas da superf´cie cuja equacao em coordenadas cartesia-
ı ı
´
nas e dada
(a) x2 + y2 + 4z2 = 16 (c) x2 − y2 = 3z2
(b) x 2 − y2 = 9 (d) x2 + y2 = z2
¸˜ ¸˜
6.3.2. Encontre uma equacao em coordenadas esf´ ricas da superf´cie cuja equacao em coordenadas cartesianas
e ı
´
e dada
(a) x2 + y2 + z2 = 9z (c) x2 + y2 = 9
(b) x 2 + y2 = z2 (d) x2 + y2 = 2z
¸˜ ¸˜
6.3.3. Encontre uma equacao em coordenadas cartesianas da superf´cie cuja equacao em coordenadas
ı
´
cil´ndricas e dada
ı
(a) r = 4 (c) r2 cos 2θ = z3
(b) r = 3 cos θ (d) z2 sen θ = r3
¸˜ ¸˜
6.3.4. Encontre uma equacao em coordenadas cartesianas da superf´cie cuja equacao em coordenadas esf´ ricas
ı e
´
e dada
(a) φ = π/4 (c) r = 2 tan θ
(b) r = 9 sec φ (d) r = 6 sen φ sen θ + 3 cos φ
¸˜
6.3.5. Determine representacoes param´ tricas para as seguintes superf´cies:
e ı
x 2 y 2 z 2
(a) − 2 + 2 − 2 = 1 (d) f ( x, y) = 0
a b c x y
x2 y2 (e) f ( , ) = 0
(b) z = − 2 + 2 z z
a b (f) f ( x2 + y2 , z) = 0
x2 y2 (g) f ( x − az, y − bz) = 0.
(c) z2 = 2 + 2
a b
´
6.3.6. Mostre que a cubica retorcida
x = t, y = t2 e z = t3
est´ contida no cilindro de equacao y = x2 .
a ¸˜
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

463. 6.3 ı e ¸˜
Coordenadas Cil´ndricas, Esf´ ricas e Equacoes Param´ tricas
e 451
ˆ
6.3.7. Mostre que a h´ lice conica
e
x = t cos t, y = t sen t e z=t
est´ contida no cone de equacao z2 = x2 + y2 .
a ¸˜
6.3.8. Determine uma parametrizacao para a curva obtida da intersecao do cilindro de equacao x2 + y2 = 1
¸˜ ¸˜ ¸˜
com o plano y + z = 2
Marco 2012
¸ Reginaldo J. Santos

464. 7
Mudanca de Coordenadas
¸
7.1 ¸˜ ¸˜
Rotacao e Translacao
Se as coordenadas de um ponto P no espaco s˜ o ( x, y, z), ent˜ o as componentes do
¸ a a
−→
vetor OP tamb´ m s˜ o ( x, y, z) e ent˜ o podemos escrever
e a a
−→
OP = ( x, y, z) = ( x, 0, 0) + (0, y, 0) + (0, 0, z)
= x (1, 0, 0) + y(0, y, 0) + z(0, 0, 1) = xi + y j + zk,
em que i = (1, 0, 0), j = (0, 1, 0) e k = (0, 0, 1). Ou seja, as coordenadas de um ponto
−→
P s˜ o iguais aos escalares que aparecem ao escrevermos OP como uma combinacao
a ¸˜
linear dos vetores canonicos. Assim, o ponto O = (0, 0, 0) e os vetores i, j e k de-
ˆ
452

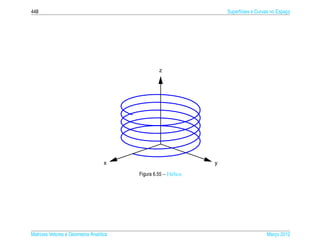
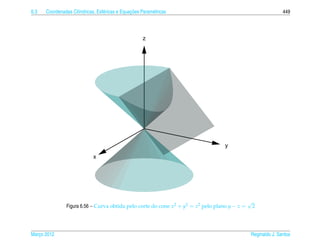
465. 7.0 ¸˜ ¸˜
Rotacao e Translacao 453
terminam um sistema de coordenadas ortogonal, {O, i, j, k}. Para resolver alguns
e ´
problemas geom´ tricos e necess´ rio usarmos um segundo sistema de coordenadas
a
ortogonal determinado por uma origem O e por vetores U1 , U2 e U3 unit´ rios e
√ a
mutuamente ortogonais. ∗ Por exemplo, se O = (2, 3/2, 3/2), U = ( 3/2, 1/2, 0),
√ 1
U2 = (−1/2, 3/2, 0) e U3 = (0, 0, 1) = k, ent˜ o {O , U1 , U2 , U3 } determina um
a
novo sistema de coordenadas: aquele com origem no ponto O , cujos eixos x , y e z
s˜ o retas que passam por O orientadas com os sentidos e direcoes de U1 , U2 e U3 ,
a ¸˜
respectivamente.
As coordenadas de um ponto P no sistema de coordenadas {O , U1 , U2 , U3 } e defi-
´
−→
nido como sendo os escalares que aparecem ao escrevermos O P como combinacao
¸˜
linear dos vetores U1 , U2 e U3 , ou seja, se
−→
O P= x U1 + y U2 + z U3 ,
ent˜ o as coordenadas de P no sistema {O , U1 , U2 , U3 } s˜ o dadas por
a a
 
x
[ P]{O ,U1 ,U2 ,U3 } =  y .
z
−→
Vamos considerar inicialmente o caso em que O = O . Assim, se OP= ( x, y, z), ent˜ o
a
−→
x U1 + y U2 + z U3 =OP pode ser escrito como
  
x x
[ U1 U2 U3 ]  y  =  y 
z z
∗ Em geral, um sistema de coordenadas (n˜ o necessariamente ortogonal) e definido por um ponto O e trˆ s vetores V , V e V n˜ o
´ e
a 1 2 3 a
coplanares (n˜ o necessariamente ortogonais e unit´ rios) (veja o Exerc´cio 7.1.6 na p´ gina 462).
a a ı a
Marco 2012
¸ Reginaldo J. Santos

466. 454 Mudanca de coordenadas
¸
Multiplicando-se a esquerda pela transposta da matriz Q = [ U1 U2 U3 ], obtemos
`
 t     t  
U1 x U1 x
 U t  [ U1 U2 U3 ]  y  =  U t   y 
2 2
U3t z U3t z
Mas, como U1 , U2 e U3 s˜ o unit´ rios e mutuamente ortogonais, ent˜ o
a a a
t
   t t t
  
U1 U1 U1 U1 U2 U1 U3 U1 · U1 U1 · U2 U1 · U3
Qt Q =  U2  [ U1 U2 U3 ] =  U2 U1
t t t
U2 U2 t
U2 U3  =  U2 · U1 U2 · U2 U2 · U3  = I3
t
U3 t
U3 U1 t
U3 U2 t
U3 U3 U3 · U1 U3 · U2 U3 · U3
Assim, a matriz Q = [ U1 U2 U3 ] e invert´vel e Q−1 = Qt . Desta forma as coorde-
´ ı
nadas de um ponto P no espaco em relacao ao sistema {O, U1 , U2 , U3 } est˜ o bem
¸ ¸˜ a
definidas, ou seja, x , y e z est˜ o unicamente determinados e s˜ o dados por
a a
   
x x
[ P]{O,U1 ,U2 ,U3 } =  y  = Qt  y  = Qt [ P]{O,i, j,k} .
z z
¸˜ ´
Tamb´ m no plano temos o mesmo tipo de situacao que e tratada de forma inteira-
e
mente an´ loga. As coordenadas de um ponto P no plano em relacao a um sistema de
a ¸˜
coordenadas {O , U1 , U2 }, em que U1 e U2 s˜ o vetores unit´ rios e ortogonais, e defi-
a a ´
−→
nido como sendo os escalares que aparecem ao escrevermos O P como combinacao
¸˜
linear de U1 e U2 , ou seja, se
−→
O P= x U1 + y U2 ,
ent˜ o as coordenadas de P no sistema {O , U1 , U2 } s˜ o dadas por
a a
x
[ P]{O ,U1 ,U2 } = .
y
Matrizes Vetores e Geometria Anal´tica
ı Marco 2012
¸

467. 7.0 ¸˜ ¸˜
Rotacao e Translacao 455
Vamos considerar, tamb´ m no plano, inicialmente o caso em que O = O . Assim, se
e
−→ −→
OP= ( x, y), ent˜ o x U1 + y U2 =OP pode ser escrito como