1. O documento apresenta notas de aulas sobre equações diferenciais ordinárias de primeira e segunda ordem. 2. São discutidos conceitos preliminares como problemas onde surgem EDOs, existência e unicidade de soluções. 3. Também são apresentados métodos de resolução de EDOs lineares e não lineares de primeira e segunda ordem, como equações exatas, variáveis separáveis, transformada de Laplace e sistemas de equações.

1. ˜
UNIVERSIDADE DE SAO PAULO
ˆ ´ ˜
INSTITUTO DE CIENCIAS MATEMATICAS DE SAO CARLOS
DEPARTAMENTO DE MATEMATICA APLICADA E ESTAT´
´ ISTICA
¸˜ ´
EQUACOES DIFERENCIAIS ORDINARIAS
NOTAS DE AULAS
Herminio Cassago Junior
Luiz Augusto da Costa Ladeira
˜
SAO CARLOS - SP
2011

2. Sum´rio
a
1 Preliminares 1
1.1 Problemas onde surgem E.D.O. . . . . . . . . . . 2
1.1.1 Um Problema Geometrico . . . . . . . . .
´ 2
1.1.2 ımico . . . . . . . . . . . .
Um Problema Qu´ 3
1.1.3 ısicos . . . . . . . . . . . . . . .
Problemas F´ 3
1.2 Existencia e Unicidade de Solucoes . . . . . . .
ˆ ¸˜ 7
2 Equa¸˜o Diferencial Linear de Primeira Ordem
ca 15
2.1 A Equacao Homogenea . . . . . . . . . . . . . . .
¸˜ ˆ 17
2.2 A Equacao nao Homogenea . . . . . . . . . . . .
¸˜ ˜ ˆ 19
2.3 Algumas Aplicacoes . . . . . . . . . . . . . . . . .
¸˜ 24
2.3.1 Desintegracao radioativa . . . . . . . . .
¸˜ 24
2.3.2 Circuito Eletrico . . . . . . . . . . . . . . .
´ 25
2.3.3 Resfriamento de um corpo . . . . . . . . . 26
i

3. 2.3.4 Diluicao de Misturas . . . . . . . . . . . .
¸˜ 28
2.3.5 Outras Aplicacoes . . . . . . . . . . . . . .
¸˜ 30
3 Equa¸˜es Lineares de Segunda Ordem
co 31
3.1 Teoria Geral para Equacoes de Segunda Ordem 33
¸˜
3.2 Reducao de Ordem . . . . . . . . . . . . . . . . . .
¸˜ 41
3.3 ¸˜ ˆ
Equacoes Homogeneas com Coeficientes Cons-
tantes . . . . . . . . . . . . . . . . . . . . . . . . . . 43
3.4 A Equacao Nao Homogenea . . . . . . . . . . . .
¸˜ ˜ ˆ 52
3.4.1 ´
Metodo dos Coeficientes a Determinar 55
3.4.2 ´ ¸˜ ˆ
Metodo de Variacao dos Parametros (ou
Variaca
¸ ˜ o das Constantes) . . . . . . . . . 64
3.5 Algumas Aplicacoes . . . . . . . . . . . . . . . . .
¸˜ 67
3.5.1 Vibracoes Mecanicas . . . . . . . . . . . . .
¸˜ ˆ 67
3.5.2 Circuitos Eletricos . . . . . . . . . . . . .
´ 70
3.5.3 Outras Aplicacoes . . . . . . . . . . . . . .
¸˜ 72
3.6 Equacoes de Ordem Superior . . . . . . . . . . .
¸˜ 73
3.7 Metodo dos Coeficientes a Determinar . . . .
´ 79
3.8 Metodo de Variacao dos Parametros . . . . . .
´ ¸˜ ˆ 80
4 Transformada de Laplace 82
4.1 Integrais Improprias . . . . . . . . . . . . . . . . .
´ 82

4. 4.2 A Transformada de Laplace . . . . . . . . . . . . 84
4.3 Algumas Propriedades . . . . . . . . . . . . . . . . 85
4.4 Transformada Inversa - Fracoes Parciais . .
¸˜ 89
4.5 Aplicacao a Equacoes Diferenciais . . . . . . .
¸˜ ¸˜ 92
4.6 Outras Propriedades . . . . . . . . . . . . . . . . . 94
4.7 Delta de Dirac . . . . . . . . . . . . . . . . . . . . . 97
4.7.1 Transformada de Laplace de δ(t − t0 ) . . 98
4.8 O Produto de Convolucao . . . . . . . . . . . . . 100
¸˜
4.9 Tabela de Algumas Transformadas . . . . . . . 103
5 Sistemas de Equa¸˜es Diferenciais
co 105
5.1 Teoria Geral para Sistemas . . . . . . . . . . . . . . . . 107
5.2 Sistemas Lineares com Coeficientes Constantes116
5.3 ˜ ˆ
Sistemas Lineares nao Homogeneos com Coefi-
cientes Constantes . . . . . . . . . . . . . . . . . . 128
5.4 Metodo da Variacao dos Parametros . . . . . . 131
´ ¸˜ ˆ
5.5 ¸˜
Resolucao de Sistemas pela Transformada de
Laplace . . . . . . . . . . . . . . . . . . . . . . . . . 135
6 Equa¸˜es N˜o Lineares de Primeira Ordem
co a 138
6.1 Equacoes Exatas . . . . . . . . . . . . . . . . . . . 138
¸˜
6.2 Equacoes com Variaveis Separaveis . . . . . . . 144
¸˜ ´ ´

5. 6.3 Fatores Integrantes . . . . . . . . . . . . . . . . . 146
6.4 Equacoes Homogeneas . . . . . . . . . . . . . . . . 148
¸˜ ˆ
6.5 ¸˜
Homogeneizacao . . . . . . . . . . . . . . . . . . . 150
Respostas dos Exerc´
ıcios 154
Referˆncias Bibliogr´ficas
e a 167

6. Cap´
ıtulo 1
Preliminares
O objetivo deste curso ´ mostrar alguns m´todos de resolu¸˜o de
e e ca
alguns tipos de equa¸oes diferenciais que aparecem mais freq¨ente-
c˜ u
mente.
Uma equa¸˜o diferencial ´ uma rela¸˜o que envolve uma “fun¸˜o
ca e ca ca
inc´gnita” e suas derivadas ou diferenciais. Por exemplo:
o
dy
(1) y(t) = f (t), em que y denota
˙ ˙ .
dt
(2) y (t) + y(t) = 0.
¨
(3) y (3) (t) + (sen t) y (t) + 5 t y(t) = 0.
¨
∂ 2 u(t, x) ∂ 2 u(t, x)
(4) + = 0.
∂ t2 ∂ x2
(5) M (x, y) dx + N (x, y) dy = 0.
Uma equa¸˜o diferencial ordin´ria (E.D.O.) ´ uma equa¸ao di-
ca a e c˜
ferencial na qual a fun¸ao inc´gnita depende apenas de uma vari´vel.
c˜ o a
1

7. Preliminares Cap. 1 Onde surgem E.D.O. 2
As equa¸oes (1), (2), (3) e (5) acima s˜o exemplos de equa¸oes dife-
c˜ a c˜
renciais ordin´rias. Se a fun¸˜o inc´gnita depender de mais de uma
a ca o
a ca ´
vari´vel, temos uma equa¸˜o diferencial parcial (E.D.P.). E o caso
da equa¸ao (4). Estaremos interessados exclusivamente nas E.D.O.’s.
c˜
A ordem de uma equa¸˜o diferencial ´ a ordem da mais alta
ca e
derivada da fun¸ao inc´gnita. Portanto, (1) ´ uma equa¸ao de primeira
c˜ o e c˜
ordem, (2) ´ de segunda ordem e (3) ´ de terceira ordem.
e e
Uma solu¸˜o de uma equa¸ao diferencial ´ uma fun¸ao definida
ca c˜ e c˜
num intervalo que, juntamente com suas derivadas, satisfaz a equa¸ao
c˜
diferencial dada. Por exemplo, a fun¸ao y(t) = sen t ´ uma solu¸ao da
c˜ e c˜
E.D.O. de segunda ordem y + y = 0, pois,
¨
d2 sen t
+ sen t = − sen t + sen t = 0.
dt2
Verifique que, para cada c ∈ R, a fun¸ao yc (t) = c ek t ´ uma
c˜ e
solu¸ao da E.D.O. de primeira ordem y = k y e que yc (t) = c t ´ uma
c˜ ˙ e
solu¸ao de E.D.O. de segunda ordem y = 0.
c˜ ¨
1.1 Problemas onde surgem E.D.O.
1.1.1 ´
Um Problema Geometrico
Determine uma curva que seja definida pela condi¸˜o de ter em todos
ca
dy
os pontos (x, y) a inclina¸ao
c˜ igual ao dobro da soma das coorde-
dx
nadas do ponto.
Se y = y(x) ´ a equa¸ao da curva, ent˜o, para resolver este pro-
e c˜ a
blema devemos resolver a equa¸˜o diferencial:
ca
dy
= 2 (x + y).
dx

8. Preliminares Cap. 1 Onde surgem E.D.O. 3
1.1.2 Um Problema Qu´
ımico
Suponha que 100 gramas de a¸ucar de cana, em agua, est˜o sendo
c´ ´ a
transformados em dextrose numa raz˜o que ´ proporcional ` quanti-
a e a
dade n˜o transformada. Deseja-se saber quanto a¸ucar foi transfor-
a c´
mado ap´s t minutos.
o
Se q ´ o n´mero de gramas convertido em t minutos e k ´ a cons-
e u e
tante de proporcionalidade, ent˜o, a equa¸ao deste problema ´ dada
a c˜ e
por:
dq
= k (100 − q),
dt
sabendo-se que q(0) = 0.
1.1.3 Problemas F´
ısicos
1. Movimento vertical
Vamos descrever o movimento vertical de um corpo de massa m sob
a a¸ao da gravidade em um meio que oferece resistˆncia proporcional
c˜ e
a velocidade do corpo. Deseja-se conhecer a posi¸ao do corpo num
` c˜
instante t.
Seja y = y(t) a posi¸ao do corpo no instante t.
c˜
Consideremos o sentido positivo o do movimento, Tv = ky
k ˙
isto ´, para baixo. As for¸as que atuam sobre o
e c
m
corpo de massa m s˜o: m g devido a gravidade (no
a `
dy mg
sentido do movimento) e k devido a resistˆncia
` e c
dt
do meio (no sentido contr´rio ao movimento).
a
Segue da 2a lei de Newton (F = m a) que a equa¸ao do movimento
¯ c˜
´ dada por
e
d2 y dy
m 2 = mg − k .
dt dt

9. Preliminares Cap. 1 Onde surgem E.D.O. 4
Conhecendo y(0) = y0 e y(0) = 0, determinamos a posi¸˜o do
˙ ca
corpo em qualquer instante.
2. Movimento de um pˆndulo simples
e
x T
E
s θ
d
d x
θ d{ E
~m mg
y c
c
cy
As for¸as que atuam no corpo de massa m s˜o a tens˜o T da corda
c a a
(de comprimento ) e a for¸a vertical mg devido ` gravidade. Se θ ´ o
c a e
a lei de Newton
deslocamento angular da corda a partir da vertical, a 2¯
nos fornece as equa¸oes:
c˜
m y = m g − T cos θ,
¨
m x = −T sen θ.
¨
Eliminando-se T e lembrando que x = sen θ e y = cos θ, obtemos a
equa¸ao do pˆndulo
c˜ e
¨ g
θ + sen θ = 0.
Note que ´ uma equa¸˜o diferencial de 2a ordem.
e ca ¯
3. Circuitos el´tricos simples
e
(i) Considere o circuito da figura abaixo em que
E
I R= resistˆncia
e
R

10. I= corrente
E
L L= indutˆncia
a
E= for¸a eletromotriz
c

11. Preliminares Cap. 1 Onde surgem E.D.O. 5
Sabe-se que a queda de potencial atrav´s da resistˆncia R ´ RI e
e e e
dI
atrav´s da indutˆncia L ´ L
e a e . Segundo a lei de Kirchhoff, a queda
dt
total de potencial no circuito deve ser contrabalanceada pela for¸ac
eletromotriz aplicada. Com isso, a corrente num instante t qualquer ´e
dada pela equa¸˜o diferencial:
ca
dI
L + R I = E,
dt
que ´ uma equa¸ao diferencial de 1a ordem.
e c˜ ¯
(ii) Dado o circuito
E em que R, I, L e E s˜o como em
a
I (i) e C = capacitˆncia. Sabe-se que
a
R

12. a queda de potencial atrav´s da ca-
e
E
L 1
pacitˆncia C ´ Q, em que Q ´ a carga
a e e
C
C no capacitor. Pela lei de Kirchhoff
temos:
dI 1
L + R I + Q = E.
dt C
dQ
Como I = , segue-se que
dt
d2 Q dQ 1
L +R + Q = E,
dt2 dt C
que ´ uma equa¸ao diferencial de 2a ordem.
e c˜ ¯
4. Sistema massa-mola
Consideremos uma mola (que supomos sem massa) suspensa ver-
ticalmente tendo sua extremidade superior presa num suporte r´ ıgido.
Quando fixamos um corpo de massa m na outra extremidade da mola,
ela se distende de uma quantidade d e, pela lei de Hooke, passa a exer-
cer sobre o corpo uma for¸a de intensidade kd (em que k ´ a constante
c e

13. Preliminares Cap. 1 Onde surgem E.D.O. 6
de restaura¸˜o da mola) e sentido oposto ao deslocamento. Sobre este
ca
corpo atuam duas for¸as: o peso m g e a for¸a restauradora da mola
c c
k d.
o
d
T kd
c 0
Tg
m
c
k (d + y)
y T
c cg
m
Como o corpo est´ em equil´
a ıbrio, temos
m g = k d. (1.1)
Imaginemos agora que este corpo seja deslocado verticalmente a partir
desta posi¸ao de equil´
c˜ ıbrio e, em seguida, liberado. Queremos estudar
o seu movimento. Fixemos um eixo de coordenadas Oy cuja origem
coincide com o ponto de equil´ ıbrio do corpo e sentido para baixo. As
for¸as que atuam sobre o corpo s˜o: o peso m g (mesmo sentido de Oy)
c a
e a for¸a restauradora da mola de sentido oposto ao do deslocamento
c
e intensidade k (y + d). Pela 2a lei de Newton, temos:
¯
d2 y
m = m g − k (y + d).
dt2
Usando (1.1), obtemos
d2 y
m + k y = 0,
dt2
que ´ uma equa¸ao diferencial linear de 2a ordem.
e c˜ ¯

14. Preliminares Cap. 1 Existˆncia e Unicidade
e 7
1.2 ˆ ¸˜
Existencia e Unicidade de Solucoes
Seja f : [a, b] → R uma fun¸ao cont´
c˜ ınua. O Teorema Fundamental
do C´lculo implica que a fun¸ao
a c˜
t
F (t) = f (s) ds, com a ≤ t ≤ b,
a
´ diferenci´vel em (a, b) e F (t) = f (t) para todo t ∈ (a, b). Logo, F (t)
e a
´ uma solu¸ao da equa¸ao diferencial ordin´ria de 1a ordem
e c˜ c˜ a ¯
y(t) = f (t) com a ≤ t ≤ b,
˙
e ainda F (a) = 0. Neste caso dizemos que F (t) ´ uma solu¸ao do
e c˜
problema de valor inicial (P.V.I.)
y(t) = f (t)
˙
y(a) = 0.
Este P.V.I. possui uma solu¸ao, mas surge a pergunta:
c˜
Ser´ que F (t) ´ a unica solu¸ao deste P.V.I.? Neste caso a resposta ´
a e ´ c˜ e
positiva, pois, se G(t) for uma outra solu¸ao, temos que
c˜
G (t) = f (t) = F (t)
e isso implica que (F − G) (t) = 0. Ou seja, (F − G)(t) = constante.
Mas, (F − G)(a) = F (a) − G(a) = 0 − 0 = 0. Portanto, G(t) = F (t)
para todo t ∈ (a, b).
No entanto, h´ problemas do valor inicial que possuem mais de
a
uma solu¸ao. O problema de valor inicial
c˜
y = |y|1/2
˙
(1.2)
y(0) = 0
n˜o tem unicidade de solu¸˜o, pois y1 (t) ≡ 0 ´ uma solu¸ao e
a ca e c˜

15. Preliminares Cap. 1 Existˆncia e Unicidade
e 8
t2 /4, t ≥ 0, T y2 (t)
y2 (t) =
−t2 /4, t 0
tamb´m ´ solu¸ao (verifique).
e e c˜ E
Portanto, temos duas solu¸oes
c˜ y1 (t) ≡ 0
para o problema (1.2).
Como um outro exemplo, vemos que o P.V.I.
y = 3 y 2/3
˙
(1.3)
y(0) = 0
tamb´m n˜o tem unicidade de solu¸ao, pois y(t) ≡ 0 ´ uma solu¸˜o e
e a c˜ e ca
observamos que para qualquer c ∈ R+ , a fun¸˜o yc : R → R dada por
ca
y T
(t − c)3 , t ≥ c,
yc (t) =
0, t≤c t
E
0 c1 c2 c3 c4
tamb´m ´ solu¸ao. Logo, o P.V.I. (1.3) tem infinitas solu¸˜es.
e e c˜ co
Logo, dado o P.V.I.
y = f (t, y)
˙
(1.4)
y(t0 ) = y0 ,
onde f ´ uma fun¸ao definida num aberto A de R2 , surgem as seguintes
e c˜
quest˜es:
o
1. Como sabemos que o P.V.I. (1.4) possui de fato uma solu¸ao
c˜
sem exibi-la explicitamente?
2. Como sabemos que existe somente uma solu¸ao de (1.4)? Talvez
c˜
existam duas ou trˆs ou mesmo infinitas solu¸˜es.
e co

16. Preliminares Cap. 1 Existˆncia e Unicidade
e 9
3. Qual a utilidade de determinarmos se (1.4) possui uma unica
´
solu¸ao se n˜o somos capazes de exibi-la?
c˜ a
Para esta ultima quest˜o, podemos dizer que o fato de sabermos
´ a
que (1.4) possui uma unica solu¸ao ´ muito importante, pois a par-
´ c˜ e
tir disto poderemos usar t´cnicas computacionais para obter aprox-
e
ima¸oes da solu¸ao y(t).
c˜ c˜
Para responder a primeira quest˜o usaremos o m´todo de Pi-
a e
card. Suponhamos que f (t, x) seja uma fun¸˜o cont´
ca ınua em (t, x) e
continuamente deriv´vel em x. Observamos que y(t) ´ solu¸ao de (1.4)
a e c˜
se, e somente se,
t
y(t) = y0 + f (s, y(s)) ds.
t0
Consideremos, agora, a seq¨ˆncia yn (t) dada da seguinte forma:
ue
y0 (t) = y0 ,
t
y1 (t) = y0 + f (s, y0 (s)) ds,
t0
t
y2 (t) = y0 + f (s, y1 (s)) ds,
t0
.
.
.
t
yn (t) = y0 + f (s, yn−1 (s)) ds.
t0
As fun¸oes yn (t) s˜o chamadas iteradas de Picard. Pode-se mostrar
c˜ a
que yn (t) → y(t), quando n → ∞, para t num intervalo conveniente.
Este processo ´ conhecido por m´todo de Picard.
e e
Exemplo 1.1. Encontre uma solu¸ao para o P.V.I.
c˜
y=y
˙
y(0) = 1

17. Preliminares Cap. 1 Existˆncia e Unicidade
e 10
usando o m´todo de Picard.
e
Solucao: Observamos que, neste caso, f (t, y) = y, t0 = 0 e y0 = 1.
¸˜
A equa¸ao integral equivalente ao P.V.I. dado ´:
c˜ e
t
y(t) = 1 + y(s) ds.
0
Portanto,
y0 (t) = 1
t
y1 (t) = 1 + 1 ds = 1 + t ,
0
t t
t2
y2 (t) = 1 + y1 (s) ds = 1 + (1 + s) ds = 1 + t + ,
0 0 2!
t t
s2 t2 t3
y3 (t) = 1 + y2 (s)ds = 1 + (1 + s + ) ds = 1 + t + + ,
0 0 2! 2! 3!
.
.
.
t t
s2 sn−1
yn (t) = 1 + yn−1 (s)ds = 1 + 1+s+ + ··· + ds=
0 0 2! (n − 1)!
2 n
t t
=1+t+ + ··· + .
2! n!
2
t tn
Como et = 1 + t + + · · · + + · · ·, vemos que as iteradas de Pi-
2! n!
card yn (t) convergem para a solu¸ao y(t) = et deste P.V.I..
c˜
ıcios 1.1. 1) Construa as iteradas de Picard para o P.V.I.
Exerc´
y = 2 t (y + 1)
˙
y(0) = 0
2
e mostre que yn (t) converge para a solu¸ao y(t) = et − 1.
c˜
2) Calcule as trˆs primeiras iteradas de Picard para o P.V.I.
e
y = et + y 2
˙
y(0) = 0.

18. Preliminares Cap. 1 Existˆncia e Unicidade
e 11
Observacao 1.1. As solu¸˜es de equa¸˜es diferenciais podem n˜o
¸˜ co co a
existir para todo t real; por exemplo, a fun¸˜o y(t) = tg(t + π/4) ´
ca e
solu¸ao do P.V.I.:
c˜
y(t) = 1 + y 2 (t), y(0) = 1
˙
e est´ definida somente no intervalo
a y
(−3π/4, π/4). T
De fato, se t ∈ (−3π/4, π/4), ent˜o
a
π 1
y(t) = sec2 (t +
˙ ) t
4 E
π − 3π π
= 1 + tg2 (t + ) 4 4
4
= 1 + y 2 (t)
π
e y(0) = tg = 1.
4
Por este fato, n˜o podemos esperar que as iteradas de Picard con-
a
virjam para todo t. Para sabermos onde as iteradas de Picard con-
vergem, tentamos encontrar um intervalo no qual todas as yn (t) s˜o a
uniformemente limitadas, isto ´, existe uma constante k 0 tal que
e
|yn (t)| ≤ k para todo t ∈ (a, b). Ou seja, procuramos um retˆngulo
a
que contenha os gr´ficos de todas as iteradas de Picard.
a
O lema abaixo cuja demonstra¸ao pode ser encontrada em [4] (cf.
c˜
Lema I.1), nos mostra como encontrar tal retˆngulo.
a
Lema 1.1. Sejam a, b ∈ R e consideremos o retˆngulo
a
R = { (t, y) | t0 ≤ t ≤ t0 + a e |y − y0 | ≤ b }.
b
Defina M = max |f (t, y)| e α = min{ a, }. Ent˜o
a
(t,y)∈R M
|yn (t) − y0 | ≤ M |t − t0 | para t0 ≤ t ≤ t0 + α.

19. Preliminares Cap. 1 Existˆncia e Unicidade
e 12
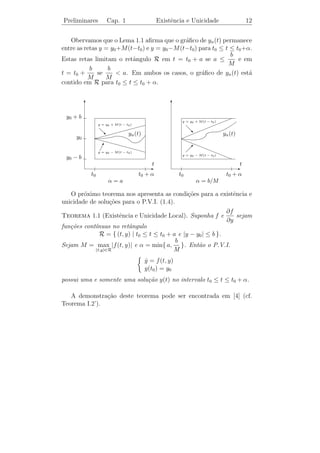
Obervamos que o Lema 1.1 afirma que o gr´fico de yn (t) permanece
a
entre as retas y = y0 +M (t−t0 ) e y = y0 −M (t−t0 ) para t0 ≤ t ≤ t0 +α.
b
Estas retas limitam o retˆngulo R em t = t0 + a se a ≤
a e em
M
b b
t = t0 + se a. Em ambos os casos, o gr´fico de yn (t) est´
a a
M M
contido em R para t0 ≤ t ≤ t0 + α.
T T
y0 + b
y = y0 + M (t − t0 )
y = y0 + M (t − t0 )
d
d
‚
d yn (t) ‚
d
yn (t)
y0
!
¡
¡
y = y0 − M (t − t0 )
y = y0 − M (t − t0 )
y0 − b
t t
E E
t0 t0 + α t0 t0 + α
α=a α = b/M
O pr´ximo teorema nos apresenta as condi¸oes para a existˆncia e
o c˜ e
unicidade de solu¸˜es para o P.V.I. (1.4).
co
∂f
Teorema 1.1 (Existˆncia e Unicidade Local). Suponha f e
e sejam
∂y
fun¸˜es cont´nuas no retˆngulo
co ı a
R = { (t, y) | t0 ≤ t ≤ t0 + a e |y − y0 | ≤ b }.
b
Sejam M = max |f (t, y)| e α = min{ a, }. Ent˜o o P.V.I.
a
(t,y)∈R M
y = f (t, y)
˙
y(t0 ) = y0
possui uma e somente uma solu¸˜o y(t) no intervalo t0 ≤ t ≤ t0 + α.
ca
A demonstra¸˜o deste teorema pode ser encontrada em [4] (cf.
ca
Teorema I.2’).

20. Preliminares Cap. 1 Existˆncia e Unicidade
e 13
Exemplo 1.2. 1) Mostre que a solu¸ao y(t) do P.V.I. y = y 2 + cos t2
c˜ ˙
1
com y(0) = 0 existe no intervalo 0 ≤ t ≤ .
2
Solucao: Usaremos o Teorema 1.1. Neste caso f (t, y) = y 2 + cos t2
¸˜
∂f
e ınuas em qualquer retˆngulo R = { (t, y) |
(t, y) = 2 y, s˜o cont´
a a
∂y
0 ≤ t ≤ a, |y| ≤ b }, em que a, b ∈ R. Calculando
M = max |f (t, y)| = max |y 2 + cos t2 | = b2 + 1,
(t,y)∈R |y|≤b e 0 ≤ t ≤ a
b
vemos que y(t) existe para 0 ≤ t ≤ α, em que α = min{ a, }.
b2 + 1
Como a priori podemos tomar qualquer valor de a, temos que o valor
b
m´ximo de α ser´ quando 2
a a for m´ximo. Este m´ximo ´ 1/2.
a a e
b +1
Portanto o Teorema 1.1 garante que a solu¸˜o y(t) existe e ´ unica
ca e ´
para 0 ≤ t ≤ 1/2.
2) Mostre que y(t) = −1 ´ a unica solu¸˜o do P.V.I. y = t(1 + y)
e ´ ca ˙
com y(0) = −1.
Solucao: Observamos que y(t) = −1 ´ solu¸ao do P.V.I.. Como
¸˜ e c˜
∂f
f (t, y) = t (1 + y) e (t, y) = t s˜o cont´
a ınuas em qualquer retˆngulo,
a
∂y
temos que o P.V.I. dado possui uma unica solu¸˜o e, portanto, ser´
´ ca a
y(t) = −1.
Observacao 1.2. Suponha que y = f (t, y) seja uma equa¸ao dife-
¸˜ ˙ c˜
rencial vetorial, isto ´, y = (y1 , . . . , yn ) ∈ Rn e f : A ⊂ Rn+1 → Rn .
e
∂f
O Teorema 1.1 continua sendo v´lido se entendermos
a como sendo
∂y
∂(f1 , . . . , fn )
a matriz jacobiana de f , isto ´, Jf =
e . Usaremos esta
∂(y1 , . . . , yn )
formula¸˜o no caso das equa¸oes de 2a ordem, das equa¸oes de ordem
ca c˜ ¯ c˜
n e de sistemas de equa¸oes diferenciais.
c˜
ıcios 1.2. 1) Determine uma solu¸˜o do P.V.I. y = t
Exerc´ ca ˙ 1 − y2

21. Preliminares Cap. 1 Existˆncia e Unicidade
e 14
com y(0) = 1 diferente de y(t) = 1. Isto contradiz o Teorema 1.1?
Explique.
2) Mostre que a solu¸ao y(t) do P.V.I. dado existe no intervalo
c˜
especificado:
a) y = t + y 2 , com y(0) = 0 para, 0 ≤ t ≤ 1/2.
˙
2
b) y = e−t + y 2 , com y(0) = 0 para, 0 ≤ t ≤ 1/2.
˙
2
c) y = e−t + y 2 , com y(1) = 0 para, 1 ≤ t ≤ 1 +
˙ e/2.
d) y = 1 + y + y 2 cos t, com y(0) = 0 para, 0 ≤ t ≤ 1/3.
˙

22. Cap´
ıtulo 2
Equa¸˜o Diferencial Linear
ca
de Primeira Ordem
Uma equa¸ao diferencial de primeira ordem pode ser colocada na
c˜
forma:
y = f (t, y),
˙ (2.1)
onde f ´ uma fun¸ao real definida em um conjunto A ⊂ R2 .
e c˜
Se a fun¸˜o f depender apenas de t, ent˜o a equa¸ao fica:
ca a c˜
y = f (t).
˙ (2.2)
Se f for integr´vel, ent˜o para resolver (2.2) integramos ambos os
a a
membros em rela¸ao a t, o que nos fornece:
c˜
y(t) = f (t) dt + c,
em que c ´ uma constante arbitr´ria e
e a f (t) dt ´ qualquer primitiva
e
de f .
15

23. Eq. Linear de 1a Ordem Cap. 2
¯ Equa¸˜o Homogˆnea 16
ca e
Este procedimento ´ imposs´ na maioria dos casos e, portanto,
e ıvel
n˜o conseguiremos resolver, sem o aux´ de computadores, a maio-
a ılio
ria das equa¸oes diferenciais. Partiremos, ent˜o, de equa¸oes mais
c˜ a c˜
simples, as quais poderemos resolver, que s˜o as lineares.
a
Definicao 2.1. Uma equa¸˜o diferencial linear de primeira
¸˜ ca
ordem ´ uma equa¸˜o da forma:
e ca
y + a(t) y = b(t),
˙ (2.3)
em que a(t) e b(t) s˜o fun¸˜es cont´nuas num intervalo I.
a co ı
Observacao 2.1. A equa¸ao (2.3) ´ chamada linear pois, se a es-
¸˜ c˜ e
crevermos na forma (2.1), teremos f (t, y) = −a(t) y + b(t) e a parte
que depende de y, isto ´, g(t, y) = −a(t) y ´ linear em y. De fato,
e e
g(t, α1 y1 + α2 y2 ) = −a(t) [α1 y1 + α2 y2 ] = −α1 a(t) y1 − α2 a(t) y2 =
α1 g(t, y1 ) + α2 g(t, y2 ).
Observacao 2.2. O P.V.I.
¸˜
y + a(t) y = b(t)
˙
y(t0 ) = y0
possui solu¸˜o unica. Isto segue do Teorema 1.1, pois as fun¸˜es
ca ´ co
∂f
f (t, y) = −a(t) y + b(t) e (t, y) = −a(t) s˜o cont´
a ınuas em t e
∂y
em y.
Exemplo 2.1. 1. y = t2 y + sen t ´ uma equa¸ao diferencial linear
˙ e c˜
a ordem, pois neste caso g(t, y) = t2 y ´ linear em y.
de 1¯ e
2. y = t y 2 + sen t n˜o ´ E.D.O. linear de 1a ordem, pois g(t, y) =
˙ a e ¯
t y 2 n˜o ´ linear em y.
a e
3. y = t cos y + t n˜o ´ E.D.O. linear de 1a ordem, pois g(t, y) =
˙ a e ¯
t cos y n˜o ´ linear em y.
a e

24. Eq. Linear de 1a Ordem Cap. 2
¯ Equa¸˜o Homogˆnea 17
ca e
2.1 ¸˜ ˆ
A Equacao Homogenea
Como uma solu¸˜o da equa¸˜o (2.3) n˜o ´ imediata, vamos simplific´-
ca ca a e a
la ainda mais, colocando b(t) ≡ 0. Obtemos
y + a(t) y = 0
˙ (2.4)
que ´ chamada equa¸˜o diferencial linear homogˆnea [L.H.] as-
e ca e
sociada a (2.3). A equa¸ao (2.3) ´ chamada equa¸˜o diferencial
c˜ e ca
linear n˜o homogˆnea [L.N.H.].
a e
A equa¸ao (2.4) pode ser resolvida facilmente. Dividindo ambos
c˜
os membros da equa¸˜o por y, obtemos:
ca
y
˙
= −a(t).
y
y
˙ d
Lembrando que = ( ln |y(t)| ) temos que a equa¸˜o (2.4) pode ser
ca
y dt
escrita na forma
d
( ln |y(t)| ) = −a(t).
dt
Integrando ambos os membros, obtemos
ln |y(t)| = − a(t) dt + c1 ,
em que c1 ´ uma constante de integra¸˜o. Tomando exponenciais de
e ca
ambos os membros, encontramos
|y(t)| = exp(− a(t) dt + c1 ).
Logo,
y(t) = c exp(− a(t) dt). (2.5)
Observamos que y(t), dada por (2.5), ´ uma solu¸ao de (2.4). Pode-
e c˜
mos dizer mais, qualquer outra solu¸˜o de (2.4) ser´ desta forma para
ca a

25. Eq. Linear de 1a Ordem Cap. 2
¯ Equa¸˜o Homogˆnea 18
ca e
algum c ∈ R. Neste caso dizemos que (2.5) ´ a solu¸˜o geral da
e ca
equa¸ao diferencial linear homogˆnea.
c˜ e
Exemplo 2.2. Determine a solu¸˜o geral da equa¸˜o: y + 2 t y = 0.
ca ca ˙
Solucao: Neste caso a(t) = 2 t. Logo,
¸˜
2
y(t) = c e− a(t) dt
= c e− 2 t dt
= c e−t .
Portanto,
2
y(t) = c e−t
´ a solu¸ao geral.
e c˜
Exemplo 2.3. Determine a solu¸ao do P.V.I.: y + (sen t) y = 0 com
c˜ ˙
y(0) = 2.
Solucao: Aqui a(t) = sen t. Logo,
¸˜
y(t) = c e− sen t dt
= c ecos t
e, portanto, a solu¸ao geral ´
c˜ e
y(t) = cecos t .
Como y(0) = 2, temos
2 = y(0) = c ecos 0 ,
o que implica que c = 2e−1 . Logo, a solu¸ao do P.V.I. ser´
c˜ a
y(t) = 2 ecos t−1 .
Exerc´ ıcios 2.1. (1) Determine a solu¸ao do P.V.I. y + et y = 0 com
c˜ ˙
y(0) = 3/2.
(2) Determine o comportamento, quando t → ∞, de todas as
solu¸oes da equa¸ao y + a y = 0, em que a ´ constante.
c˜ c˜ ˙ e

26. Eq. Linear de 1a Ordem Cap. 2
¯ Eq. n˜o Homogˆnea 19
a e
(3) Mostre que o conjunto das solu¸˜es de (2.4) possui as seguintes
co
propriedades:
i) Se y1 e y2 s˜o solu¸˜es, ent˜o y1 + y2 tamb´m ´ solu¸ao.
a co a e e c˜
ii) Se y1 ´ solu¸ao, ent˜o c y1 tamb´m ´ solu¸ao, para todo c ∈ R.
e c˜ a e e c˜
iii) A fun¸˜o y(t) ≡ 0 ´ solu¸ao.
ca e c˜
Observacao 2.3. O exerc´ (3) nos diz que o conjunto das solu¸oes
¸˜ ıcio c˜
de (2.4) ´ um espa¸o vetorial. Como toda solu¸˜o de (2.4) ´ da
e c ca e
forma (2.5), segue-se que este espa¸o vetorial tem dimens˜o 1 e que
c a
y1 (t) = e− a(t) dt ´ uma base para este espa¸o.
e c
2.2 ¸˜ ˜ ˆ
A Equacao nao Homogenea
Consideremos agora a equa¸ao n˜o homogˆnea
c˜ a e
y + a(t) y = b(t).
˙ (2.6)
Se consegu´
ıssemos escrever a equa¸ao acima como
c˜
d
(“algo”) = b(t),
dt
o nosso problema estaria resolvido, pois bastaria integrar ambos os
membros para encontrar o valor de “algo”. Por´m, a express˜o y +
e a ˙
a(t)y n˜o aparece como derivada de alguma express˜o simples. Para
a a
resolvermos o problema procuraremos uma fun¸˜o µ(t), cont´
ca ınua e
diferenci´vel tal que multiplicando-se ambos os membros da express˜o
a a
(2.6) por µ(t) obteremos a equa¸ao equivalente:
c˜
µ(t)y + µ(t)a(t)y = µ(t)b(t)
˙ (2.7)
(onde, por equa¸˜o equivalente entendemos que toda solu¸˜o de (2.7)
ca ca
´ uma solu¸ao da (2.6) e reciprocamente) de modo que o primeiro
e c˜
membro de (2.7)
µ(t) y + µ(t) a(t) y
˙

27. Eq. Linear de 1a Ordem Cap. 2
¯ Eq. n˜o Homogˆnea 20
a e
seja a derivada de alguma express˜o simples.
a
Observamos que
d
(µ(t)y) = µ(t) y + µ(t) y.
˙ ˙
dt
Portanto,
d
µ(t) y + a(t) µ(t) y =
˙ (µ(t) y) ⇔ µ(t) = a(t) µ(t)
˙
dt
a(t) dt
⇔ µ(t) − a(t) µ(t) = 0 ⇔ µ(t) = e
˙ .
Logo, para esta µ(t) a equa¸˜o (2.6) pode ser escrita como:
ca
d
(µ(t) y) = µ(t) b(t).
dt
Por integra¸ao obtemos
c˜
µ(t) y = µ(t) b(t) dt + c
ou
1
y(t) = [ µ(t) b(t) dt + c] = e− a(t) dt
[c + e a(t) dt
b(t) dt].
µ(t)
Portanto,
y(t) = c e− a(t) dt
+ e− a(t) dt
e a(t) dt
b(t) dt (2.8)
´ a solu¸˜o geral da equa¸ao n˜o homogˆnea.
e ca c˜ a e
Observacao 2.4. Vemos que a 1a parcela da f´rmula (2.8) ´ a
¸˜ ¯ o e
solu¸ao geral da homogˆnea associada e que
c˜ e
yp (t) = e− a(t) dt
e a(t) dt
b(t) dt
´ uma solu¸˜o particular da equa¸˜o n˜o homogˆnea (obtida quando
e ca ca a e
c = 0). Logo, a solu¸ao geral da [L.N.H.] ´ a soma da geral da [L.H.]
c˜ e
asssociada com uma particular da [L.N.H.].

28. Eq. Linear de 1a Ordem Cap. 2
¯ Eq. n˜o Homogˆnea 21
a e
Observacao 2.5. A fun¸ao µ(t) = e a(t) dt ´ chamada fator inte-
¸˜ c˜ e
grante para a equa¸˜o n˜o homogˆnea.
ca a e
Observacao 2.6. Um outro m´todo de resolver uma equa¸˜o [L.N.H.]
¸˜ e ca
´ o chamado m´todo da varia¸˜o das constantes, que consiste em
e e ca
fazer
y = uv
que implica
y = u v + u v.
˙ ˙ ˙
Logo, a equa¸˜o [L.N.H.], y + a(t) y = b(t), se torna
ca ˙
u v + v u + a(t) u v = b(t),
˙ ˙
ou seja,
u(v + a(t) v) + (v u − b(t)) = 0.
˙ ˙
Se cada termo for nulo, ent˜o esta equa¸˜o ser´ satisfeita. Portanto,
a ca a
fazendo
v + a(t) v = 0 e v u − b(t) = 0
˙ ˙
e resolvendo a primeira delas, obteremos v em fun¸˜o de t (n˜o se
ca a
acrescenta constante de integra¸˜o porque se deseja um simples valor
ca
de v). Em seguida, substituindo este valor na segunda equa¸ao e
c˜
integrando, obteremos o valor de u (agora acrescentamos a constante
de integra¸˜o pois desejamos que y = uv seja a solu¸˜o geral do pro-
ca ca
blema).
Exemplo 2.4. Determine a solu¸˜o geral da equa¸˜o: y + 2 t y = t.
ca ca ˙
Solucao: Aqui a(t) = 2 t. Logo,
¸˜
a(t) dt 2 t dt 2
µ(t) = e =e = et .
Multiplicando-se ambos os membros da equa¸ao por µ(t), obtemos a
c˜
equa¸ao equivalente:
c˜
2 2 d 2 2
et (y + 2 t y) = t et
˙ ou (y et ) = t et .
dt

29. Eq. Linear de 1a Ordem Cap. 2
¯ Eq. n˜o Homogˆnea 22
a e
Portanto,
2 2 1 t2
y et = t et dt + c = e +c
2
que implica
2 1
y(t) = c e−t + .
2
Exemplo 2.5. Determine a solu¸˜o do P.V.I.: y−3 t2 y = t2 , y(0) = 1.
ca ˙
Solucao: Aqui a(t) = −3 t2 . Logo
¸˜
−3t2 dt 3
µ(t) = e a(t) dt
=e = e−t .
Multiplicando-se ambos os membros por µ(t), obtemos:
3 3 d −t3 3
e−t (y − 3t2 y) = t2 e−t
˙ ou (e y) = t2 e−t .
dt
Assim,
t t
d −s3 3
(e y(s)) ds = s2 e−s ds .
0 dt 0
efetuando a integra¸ao, obtemos
c˜
3 1 3
e−t y(t) − y(0) = − (e−t − 1).
3
Como y(0) = 1, temos que
4 t3 1
y(t) = e − .
3 3
ıcios 2.2. 1) Determine a solu¸ao dos P.V.I.’s:
Exerc´ c˜
2
a) y = (cos t) y, y(0) = 1.
˙ b) y +
˙ y = t3 , y(1) = 2.
t
1
c) t y + y = t,
˙ y(10) = 20. d) y + y =
˙ , y(1) = 3.
1 + t2
1
e) (1 + t2 ) y + 4 t y = t, y(1) = .
˙
4

30. Eq. Linear de 1a Ordem Cap. 2
¯ Eq. n˜o Homogˆnea 23
a e
2) (Equacao de Bernoulli) A equa¸˜o
¸˜ ca
y + p(t)y = q(t)y n ,
˙
em que p(t) e q(t) s˜o fun¸oes cont´
a c˜ ınuas em algum intervalo I da reta
e n ∈ R, ´ conhecida como a equa¸˜o de Bernoulli. Se n = 0 e
e ca
n = 1 a equa¸ao n˜o ´ linear, mas pode ser transformada em uma
c˜ a e
equa¸ao linear fazendo a mudan¸a de vari´vel z = y 1−n . Demonstre
c˜ c a
isto, e resolva as equa¸oes:
c˜
3
a) y + t2 y = t2 y 4 .
˙ b) y −
˙ y = t4 y 1/3 .
t
2
c) y +
˙ y = −t9 y 5 , y(−1) = 2.
t
3) (Equacao de Ricatti) A equa¸˜o
¸˜ ca
y + p(t) y + q(t) y 2 = f (t),
˙ (R)
em que p(t), q(t) e f (t) s˜o fun¸oes cont´
a c˜ ınuas em algum intervalo I da
reta e q(t) = 0 em I ´ conhecida como a equa¸˜o de Ricatti. Se y1 (t)
e ca
´ uma solu¸ao particular de (R), mostre que a mudan¸a de vari´vel
e c˜ c a
y = y1 + 1/z transforma (R) numa equa¸ao linear de 1a ordem em z
c˜ ¯
da forma z = (p(t) + 2 q(t) y1 ) z + q(t). Deduza da´ que a solu¸ao geral
˙ ı c˜
de uma equa¸ao de Ricatti pode ser encontrada, desde que se conhe¸a
c˜ c
uma solu¸ao particular.
c˜
4) Use o exerc´ anterior para determinar a solu¸ao geral de cada
ıcio c˜
uma das seguintes equa¸˜es de Ricatti:
co
a) y − t3 y + t2 y 2 = 1, y1 (t) = t.
˙
b) y − t y 2 + (2t − 1) y = t − 1, y1 (t) = 1.
˙
c) y + y 2 − (1 + 2 et ) y + e2 t = 0, y1 (t) = et .
˙
d) y + t y 2 − 2 t2 y + t3 = t + 1, y1 (t) = t − 1.
˙

31. Eq. Linear de 1a Ordem Cap. 2
¯ Algumas Aplica¸˜es
co 24
2.3 ¸˜
Algumas Aplicacoes
2.3.1 ¸˜
Desintegracao radioativa
Seja N (t) o n´mero de ´tomos radioativos em uma amostra num ins-
u a
tante t. Define-se a atividade de uma amostra radioativa como sendo
o n´mero de desintegra¸oes por unidade de tempo. Foi observado
u c˜
desde o in´ do estudo da radioatividade (1896), que a atividade ´
ıcio e
proporcional ao n´mero de atomos radioativos presentes, isto ´:
u ´ e
dN
= −λ N,
dt
onde λ ´ chamada constante de desintegra¸˜o ou de decaimento
e ca
radioativo.
Se N0 ´ o n´mero de ´tomos no instante t = 0, teremos o seguinte
e u a
P.V.I.
dN
= −λ N, N (0) = N0
dt
que ´ uma equa¸˜o diferencial ordin´ria homogˆnea de 1a ordem, cuja
e ca a e ¯
solu¸ao ser´:
c˜ a
N (t) = N0 e−λ t .
Observacao 2.7. Vale uma equa¸˜o semelhante para a massa de
¸˜ ca
uma substˆncia radioativa, ou seja:
a
dm
= −λ m, m(0) = m0 ,
dt
onde m = massa.
A meia-vida de uma substˆncia radioativa ´ definida como sendo
a e
o tempo necess´rio para a decomposi¸ao da metade da substˆncia.
a c˜ a

32. Eq. Linear de 1a Ordem Cap. 2
¯ Algumas Aplica¸˜es
co 25
Exemplo 2.6. Uma quantidade de substˆncia radioativa possui ini-
a
cialmente m0 gramas e decomp˜e-se a uma raz˜o proporcional a quan-
o a `
tidade presente. Se a meia-vida da quantidade inicial ´ 2.000 anos,
e
encontre a quantidade da substˆncia depois de 3.000 anos.
a
dm m0
Solucao: Temos que
¸˜ = −λm, m(0) = m0 e m(2000) = .
dt 2
Sabemos que a solu¸ao geral desta equa¸ao ´:
c˜ c˜ e
m(t) = c e−λ t .
Como m(0) = m0 , temos que c = m0 . Portanto,
m(t) = m0 e−λ t .
Mas, 2 m0 = m0 e−2000 λ o que implica que λ =
1 ln 2
2000
. Logo, m(t) =
−(ln 2/2000)t
m0 e e, portanto,
m0
m(3000) = m0 e−(3 ln 2)/2 = √ .
8
Observacao 2.8. Pode-se usar a desintegra¸˜o radioativa para de-
¸˜ ca
scobrir a falsifica¸˜o de obras de arte (vide [4], Se¸ao 1.3).
ca c˜
2.3.2 ´
Circuito Eletrico
Consideremos um circuito el´trico simples
e E
consistindo de uma indutˆncia L, uma re-
a I R
sistˆncia R e uma for¸a eletromotriz E0 =
e c

33. constante. O circuito ´ ligado no instante
e E
L
t = 0. Deseja-se determinar a corrente
I(t). Sabe-se que:
i) a queda de voltagem (ou tens˜o) atrav´s
a e
da resistˆncia R ´ igual a RI;
e e
dI
ii) a queda de voltagem atrav´s de uma indutˆncia L ´ igual a L
e a e .
dt
Logo, pela lei de Kirchhoff que diz que a soma alg´brica das diferen¸as
e c

34. Eq. Linear de 1a Ordem Cap. 2
¯ Algumas Aplica¸˜es
co 26
de potencial ´ zero, temos:
e
dI dI RI E0
L + RI − E0 = 0 ou + =
dt dt L L
que ´ uma E.D.O. linear n˜o homogˆnea de 1a ordem. Como I(0) = 0
e a e ¯
(pois s´ temos corrente ap´s ligarmos o circuito), temos que
o o
E0
I(t) = (1 − e−R t / L ).
R
2.3.3 Resfriamento de um corpo
(1) Consideremos um modelo simplificado para o fenˆmeno de
o
varia¸˜o de temperatura num corpo por perda ou ganho de calor para
ca
o meio ambiente, fazendo as seguintes hip´teses:
o
i) A temperatura T ´ a mesma no corpo todo e depende apenas do
e
tempo.
ii) A temperatura do meio ambiente, Ta , ´ constante com o tempo.
e
˙ dT
iii) O fluxo de calor atrav´s das paredes do corpo, dado por T (t) =
e
dt
´ proporcional ` diferen¸a entre as temperaturas do corpo e do meio
e a c
ambiente, isto ´,
e
˙
T = −k(T − Ta )
(chamada lei de Newton para resfriamento) em que k ´ uma constante
e
positiva que depende das propriedades f´ ısicas do corpo. Observamos
que o sinal − na equa¸ao ´ devido ao fato que o calor flui da fonte
c˜ e
quente para a fonte fria, e assim se T Ta teremos que T decresce e
se T Ta , ent˜o T cresce. Conhecendo-se a temperatura T (0) = T0 ,
a
podemos obter a temperatura do corpo em um instante t ≥ 0 qualquer.
Para isto basta resolver a E.D.O. linear n˜o homogˆnea de 1a ordem:
a e ¯
˙
T + k T = k Ta , T (0) = T0
cuja solu¸ao ser´:
c˜ a
T (t) = (T0 − Ta )e−k t + Ta .

35. Eq. Linear de 1a Ordem Cap. 2
¯ Algumas Aplica¸˜es
co 27
Observamos que:
1) T0 Ta =⇒ T (t) decresce quando t aumenta.
2) T0 Ta =⇒ T (t) cresce quando t aumenta.
3) T0 = Ta =⇒ T (t) ´ constante.
e
4) Em todos os casos T (t) → Ta quando t → ∞, isto ´, Ta ´
e e
chamada de temperatura de equil´ ıbrio.
Geometricamente, temos
T T
T0
T (t)
Ta Ta
T (t)
T0
t t
E E
T0 Ta T0 Ta
(2) Suponhamos que a temperatura Ta , do meio ambiente, varia
com o tempo ao receber (ou ceder) calor ao corpo. Sejam m e ma ,
as massas do corpo e do meio ambiente, respectivamente e c e ca ,
os calores espec´
ıficos do corpo e do meio ambiente respectivamente.
Supondo-se que n˜o haja mudan¸as de estado f´
a c ısico, a lei da con-
serva¸˜o da quantidade de calor pode ser expressa como:
ca
mc(T0 − T ) = ma ca (Ta − Ta,0 ), (2.9)
onde T = T (t) e Ta = Ta (t) s˜o as temperaturas do corpo e do meio
a
ambiente num instante t, respectivamente, e T0 = T (0) e Ta,0 = Ta (0).

36. Eq. Linear de 1a Ordem Cap. 2
¯ Algumas Aplica¸˜es
co 28
Usando-se na equa¸˜o
ca
˙
T = −k (T − Ta )
a express˜o de Ta dada em (2.9), temos
a
mc
Ta = (T0 − T ) + Ta,0 .
ma ca
Ent˜o obtemos
a
˙ mc mc
T + k(1 + )T = k(Ta,0 + T0 ),
ma ca ma ca
que ´ uma E.D.O. linear n˜o homogˆnea de 1a ordem. A solu¸˜o desta
e a e ¯ ca
E.D.O. que satisfaz a condi¸˜o inicial T (0) = T0 ´
` ca e
T0 − Ta,0 −k (1+A) t Ta,0 + A T0
T (t) = e + ,
1+A 1+A
mc
onde A = . Logo
ma ca
1) T0 Ta,0 =⇒ T (t) decresce com o tempo.
2) T0 Ta,0 =⇒ T (t) cresce com o tempo.
3) T0 = Ta,0 =⇒ T (t) ´ constante e igual a Ta,0 .
e
Ta,0 + A T0
4) Em qualquer dos casos T (t) → , quando t → ∞, que
1+A
ser´ a temperatura de equil´
a ıbrio.
Ta,0 + A T0
ıcio: Mostre que Ta (t) →
Exerc´ , quando t → ∞.
1+A
2.3.4 ¸˜
Diluicao de Misturas
e ´ ´
Um tanque cont´m 100 litros de agua salgada. E adicionado, neste
tanque, ´gua salgada a raz˜o de 5 litros por minuto, com uma concen-
a ` a
tra¸ao de sal de 2 g/ . Ao mesmo tempo, a mistura deixa o tanque
c˜

37. Eq. Linear de 1a Ordem Cap. 2
¯ Algumas Aplica¸˜es
co 29
atrav´s de um buraco a mesma raz˜o. A mistura do tanque ´ conti-
e ` a e
nuamente agitada, de modo a manter a solu¸˜o homogˆnea (isto ´, a
ca e e
concentra¸˜o ´ a mesma em todo tanque). Se inicialmente a mistura
ca e
cont´m uma concentra¸˜o de 1 g/ , determine a concentra¸ao num
e ca c˜
instante futuro.
Solucao: Seja y(t) a quantidade de sal no tanque depois de t minutos
¸˜
do instante inicial t0 = 0. Temos que o sal est´ sendo adicionado no
a
y(t)
tanque a raz˜o de 5·2 g/min = 10 g/min e est´ saindo a raz˜o de 5
` a a ` a
100
y(t)
g/min = g/min. Assim, temos que a varia¸ao da quantidade de
c˜
20
sal no tanque ´ dada por:
e
y
y = 10 −
˙
20
que ´ uma E.D.O. linear n˜o homogˆnea de 1a ordem. Como y(0) =
e a e ¯
100 g temos que a sua solu¸ao ´
c˜ e
y(t) = 200 − 100 e−0,05 t
e, portanto, a concentra¸˜o de sal no tanque no instante t ser´
ca a
y(t)
c(t) = = 2 − e−0,05 t .
100
Note que isso mostra que a concentra¸˜o de sal no tanque tende a 2
ca
g/ , quando t → ∞.
Geometricamente, temos
T
2
c(t)
1
tE

38. Eq. Linear de 1a Ordem Cap. 2
¯ Algumas Aplica¸˜es
co 30
2.3.5 ¸˜
Outras Aplicacoes
a) Forma¸˜o de um composto qu´
ca ımico ([7], p´gina 45).
a
b) Dinˆmica de crescimento de um tumor ([4], Se¸ ao 1.8).
a c
c) Modelos de popula¸ao ([4], Se¸ao 1.5).
c˜ c˜
Exerc´ ıcios 2.3. 1) Um objeto de massa m ´ solto da posi¸ao de
e c˜
repouso em um meio que oferece resistˆncia proporcional a velocidade
e `
do objeto. Determinar a velocidade no instante t.
2) Fazer o problema proposto no Exerc´ 1, supondo que a re-
ıcio
sistˆncia do meio ´ proporcional ao quadrado da velocidade.
e e
3) Uma colˆnia de bact´rias cresce a uma raz˜o proporcional ao
o e a
n´mero de bact´rias presente. Se o n´mero duplica a cada 24 ho-
u e u
ras, quantas horas ser˜o necess´rias para que o n´mero de bact´rias
a a u e
aumente cem vezes sua quantidade original?
4) Um tanque de 200 litros de capacidade, cont´m inicialmente 40
e
litros de agua pura. A partir do instante t = 0, adiciona-se ao tanque
uma solu¸ao de salmoura com 250 gramas de sal por litro, ` raz˜o de
c˜ a a
12 /min. A mistura, suposta uniforme, escoa do tanque ` raz˜o de 8
a a
/min. Determinar
a) o tempo necess´rio para que ocorra o transbordamento;
a
b) a concentra¸ao de sal na mistura presente no tanque no instante
c˜
do transbordamento.

39. Cap´
ıtulo 3
Equa¸˜es Lineares de
co
Segunda Ordem
As equa¸oes diferenciais de 2a ordem podem, geralmente, ser es-
c˜ ¯
critas sob a forma
y = f (t, y, y),
¨ ˙ (3.1)
em que f ´ uma fun¸ao definida em um subconjunto A ⊂ R3 .
e c˜
Dizemos que uma fun¸ao y = y(t) ´ uma solu¸˜o de (3.1) no inter-
c˜ e ca
a ordem em I e y (t) = f (t, y(t), y(t))
valo I se y(t) tiver derivada de 2¯ ¨ ˙
para todo t ∈ I.
Por exemplo, as fun¸oes y1 (t) = e2 t e y2 (t) = e−2 t s˜o solu¸oes da
c˜ a c˜
equa¸ao y = 4 y, pois:
c˜ ¨
d2 (e2t ) d2 (e−2t )
y1 (t) =
¨ 2
= 4e2t = 4y1 (t) e y2 (t) =
¨ 2
= 4e−2t = 4y2 (t).
dt dt
Equa¸oes diferenciais surgem com freq¨ˆncia em problemas da F´
c˜ ue ısica,
especialmente em Mecˆnica, em virtude da 2a lei de Newton, e em
a
¯
Eletricidade, como aplica¸ao das leis de Kirchhoff. Por exemplo, o
c˜
movimento de um pˆndulo simples sem atrito (como figura abaixo) ´
e e
31

40. Eq. Dif. Linear de 2a Ordem
¯ Cap. 3 Teoria Geral 32
descrito pela equa¸˜o
ca
¨ g
θ + sen θ = 0. (3.2)
x
E
θ T
s
}
y
c
cm g
˙
Se levarmos em conta o atrito (que geralmente ´ dado por k θ), e
e
se o movimento estiver sujeito a uma for¸a externa F (t), a equa¸ao
c c˜
do pˆndulo fica
e
¨ ˙ g
θ + k θ + sen θ = F (t). (3.3)
Consideremos agora a equa¸˜o: y = 3.
ca ¨
Para obtermos a solu¸ao dessa equa¸ao basta integrarmos duas
c˜ c˜
vezes, ou seja,
3 2
y=
˙ 3 dt = 3 t + c1 =⇒ y(t) = (3t + c1 ) dt = t + c1 t + c2 .
2
Note que temos o surgimento de duas constantes arbitr´rias: c1 e c2
a
(lembremos que para a equa¸˜o de 1¯
ca a ordem somente aparecia uma
constante arbitr´ria). Logo, para termos unicidade de solu¸ao, pre-
a c˜
cisamos impor duas condi¸˜es: uma sobre a fun¸ao y(t) e outra sobre
co c˜
sua a derivada y(t) no instante t0 . Observamos que este fato est´ em
˙ a
concordˆncia com os problemas de Mecˆnica pois, para se caracterizar
a a
o movimento de um corpo, ´ preciso que sejam conhecidas sua posi¸ao
e c˜
inicial e sua velocidade inicial. Isto sugere que o problema de valor
inicial associado a equa¸˜o (3.1) seja dado por
` ca

 y = f (t, y, y)
¨ ˙
y(t0 ) = y0 (3.4)
y(t0 ) = z0 .
˙


41. Eq. Dif. Linear de 2a Ordem
¯ Cap. 3 Teoria Geral 33
Em geral ´ muito dif´ resolver a equa¸ao (3.1). Por esta raz˜o,
e ıcil c˜ a
´ usual, nas aplica-¸˜es, recorrer ao estudo de equa¸oes mais simples;
e co c˜
as lineares que s˜o modelos aproximados de muitas equa¸oes diferen-
a c˜
ciais n˜o lineares. Por exemplo, a equa¸ao (3.2), do pˆndulo, n˜o ´
a c˜ e a e
linear, mas para o estudo de pequenas oscila¸oes, costuma-se usar a
c˜
aproxima¸˜o sen θ ∼ θ e considerar a equa¸ao
ca = c˜
¨ g
θ + θ = 0,
que ´, claramente, mais simples do que (3.2). Analogamente, no lugar
e
de (3.3) costuma-se estudar a equa¸˜o
ca
¨ ˙ g
θ + k θ + θ = F (t).
3.1 ¸˜
Teoria Geral para Equacoes de Se-
gunda Ordem
A partir de agora, nossa aten¸ao estar´ voltada para as equa¸oes
c˜ a c˜
lineares, cuja forma padr˜o ´
a e
y + a(t) y + b(t) y = g(t).
¨ ˙ [L.N.H.]
Esta equa¸˜o ´ chamada linear n˜o homogˆnea. Quando g(t) ≡ 0, ela
ca e a e
torna-se
y + a(t) y + b(t) y = 0.
¨ ˙ [L.H.]
Teorema 3.1 (Existˆncia e unicidade). Se as fun¸˜es a(t), b(t) e g(t)
e co
forem cont´nuas num intervalo I, ent˜o dados t0 ∈ I e y0 , z0 ∈ R, o
ı a
P.V.I. 
 y + a(t) y + b(t) y = g(t)
¨ ˙
y(t0 ) = y0 (3.5)
y(t0 ) = z0
˙

possui uma unica solu¸˜o y = y(t), a qual est´ definida para todo
´ ca a
t ∈ I.

42. Eq. Dif. Linear de 2a Ordem
¯ Cap. 3 Teoria Geral 34
Observacao 3.1. Pelo Teorema 3.1, a unica solu¸˜o de [L.H.] tal
¸˜ ´ ca
que y(t0 ) = y(t0 ) = 0 ´ a fun¸ao y(t) = 0.
˙ e c˜
Observacao 3.2. Este teorema ´ uma consequˆncia da forma veto-
¸˜ e e
rial do Teorema 1.4 (veja Observa¸ao 1.2).
c˜
∂F
De fato: Do Teorema 1.4, temos que se F e s˜o fun¸oes
a c˜
∂x
cont´
ınuas, ent˜o o P.V.I.
a
x = F (t, x)
˙
x(t0 ) = x0
possui uma unica solu¸ao. Aqui temos a equa¸ao y = g(t) − a(t) y −
´ c˜ c˜ ¨ ˙
b(t) y que pode ser escrita na forma x = F (t, x), fazendo
˙
y = x1
y = x1 = x2 .
˙ ˙
Assim, temos que y = x2 = −a(t) x2 − b(t) x1 + g(t). Chamando
¨ ˙
x1 x2 F1 (t, x)
x= , temos x =
˙ = .
x2 −a(t) x2 − b(t) x1 + g(t) F2 (t, x)
∂F
Aqui, representa a matriz jacobiana de F (t, x1 , x2 ) em rela¸˜o a
ca
∂x
x1 , x2 , isto ´
e
∂F1 ∂F1
 
∂(F1 , F2 )  ∂x1 ∂x2  0 1
JF (t, x1 , x2 ) = = = .
 
∂(x1 , x2 )  ∂F ∂F  −b(t) −a(t)
2 2
∂x1 ∂x2
Logo, se a(t), b(t) e g(t) s˜o fun¸oes cont´
a c˜ ınuas em I, ent˜o o P.V.I.
a

 y + a(t) y + b(t) y = g(t)
¨ ˙
y(t0 ) = y0
y(t0 ) = z0
˙

possui unica solu¸ao em I.
´ c˜

43. Eq. Dif. Linear de 2a Ordem
¯ Cap. 3 Teoria Geral 35
Antes de darmos um m´todo geral que permitir´ descrever o con-
e a
junto de todas as solu¸oes de [L.H.], vamos analisar a equa¸ao
c˜ c˜
y + ω2 y = 0
¨ (3.6)
(esta ´ a equa¸˜o do pˆndulo, em que escrevemos ω = g/ ). E f´cil
e ca e ´ a
verificar que as fun¸oes ϕ1 (t) = cos ωt e ϕ2 (t) = sen ω t s˜o solu¸oes.
c˜ a c˜
Observamos que, quaisquer que sejam as constantes c1 , c2 ∈ R, a
fun¸ao
c˜
ϕ(t) = c1 cos ω t + c2 sen ω t (3.7)
tamb´m ´ solu¸ao de (3.6). De fato, calculando ϕ e ϕ temos
e e c˜ ˙ ¨
ϕ(t) = −ω c1 sen ω t + ω c2 cos ω t
˙
ϕ(t) = −ω 2 c1 cos ω t − ω 2 c2 sen ω t = −ω 2 ϕ(t).
¨
Donde,
ϕ(t) + ω 2 ϕ(t) = 0.
¨
Usando a express˜o (3.7), podemos resolver qualquer P.V.I. asso-
a
ciado ` equa¸ao(3.6). Por exemplo, se procurarmos a solu¸˜o de
a c˜ ca

 y + ω2 y = 0
¨
y(0) = 1
y(0) = 2
˙

sob a forma ϕ(t) = c1 cos ω t + c2 sen ω t, chegaremos a
1 = ϕ(0) = c1
2 = ϕ(0) = c2 ω.
˙
2
Portanto, a solu¸ao procurada ´ ϕ(t) = cos ω t +
c˜ e sen ω t.
ω
De modo an´logo, ao procurarmos a solu¸˜o do P.V.I.
a ca

 y + ω2 y = 0
¨
y(0) = y0 (3.8)
y(0) = z0
˙


44. Eq. Dif. Linear de 2a Ordem
¯ Cap. 3 Teoria Geral 36
sob a forma (3.7), chegamos a
z0
ϕ(t) = y0 cos ω t + sen ω t. (3.9)
ω
Agora, dada qualquer solu¸˜o y(t) de (3.6), chamando y0 = y(0)
ca
e z0 = y(0) vemos que y(t) ´ solu¸ao do P.V.I. (3.8). Como, pelo
˙ e c˜
Teorema 3.1, este problema possui uma unica solu¸ao, segue que
´ c˜
y(t) ≡ ϕ(t), isto ´, y ´ dada por (3.9). Logo, toda solu¸ao de (3.6)
e e c˜
´ da forma (3.7), para uma conveniente escolha de c1 e c2 . Assim,
e
se denotarmos por S o conjunto de todas as solu¸oes de (3.6), o que
c˜
acabamos de mostrar ´ que S coincide com o conjunto de todas as
e
combina¸˜es lineares de cos ω t e sen ω t (o qual ´ um espa¸o vetorial
co e c
de dimens˜o 2. Por quˆ?).
a e
Consideremos agora a equa¸˜o [L.H.] com a(t) e b(t) cont´
ca ınuas no
intervalo I. Pelo Teorema 3.1, temos que toda solu¸ao y(t) de [L.H.]
c˜
est´ definida para todo t ∈ I (al´m disso, ´ claro que y(t) ´ duas vezes
a e e e
cont´ınuamente diferenci´vel). Vamos repetir o procedimento acima e
a
mostrar que se duas solu¸oes y1 (t) e y2 (t), forem convenientemente
c˜
escolhidas, ent˜o toda solu¸ao y(t) de [L.H.] ser´ dada por
a c˜ a
y(t) = c1 y1 (t) + c2 y2 (t), (3.10)
onde c1 e c2 s˜o constantes. Primeiramente, notemos que toda fun¸˜o
a ca
da forma (3.10) ´ uma solu¸˜o de [L.H.], como mostra o pr´ximo
e ca o
teorema, conhecido como Princıpio de Superposica
´ ¸ ˜ o:
Teorema 3.2. Se ϕ1 (t) e ϕ2 (t) s˜o solu¸˜es de [L.H.] e se c1 , c2 s˜o
a co a
constantes reais, ent˜o a fun¸˜o ϕ(t) = c1 ϕ1 (t) + c2 ϕ2 (t) tamb´m ´
a ca e e
solu¸˜o de [L.H.].
ca
Demonstracao. Note que
¸˜
ϕ(t) + a(t) ϕ(t) + b(t) ϕ(t) = c1 [ϕ1 (t) + a(t) ϕ1 (t) + b(t) ϕ1 (t)]
¨ ˙ ¨ ˙
+ c2 [ϕ2 (t) + a(t) ϕ2 (t) + b(t) ϕ2 (t)] = 0,
¨ ˙

45. Eq. Dif. Linear de 2a Ordem
¯ Cap. 3 Teoria Geral 37
pois, ϕ1 e ϕ2 s˜o solu¸˜es de [L.H.]. Logo, ϕ tamb´m ´ solu¸˜o de
a co e e ca
[L.H.].
Seja y(t) uma solu¸ao de [L.H.] e sejam y0 = y(t0 ), z0 = y(t0 ) e
c˜ ˙
t0 ∈ I fixados. Para que y(t) seja dada por (3.10) devemos ter
c1 y1 (t0 ) + c2 y2 (t0 ) = y0
(3.11)
c1 y1 (t0 ) + c2 y2 (t0 ) = z0 .
˙ ˙
Podemos considerar (3.11) como um sistema de duas equa¸oes nasc˜
inc´gnitas c1 e c2 . Para que este sistema tenha solu¸ao quaisquer que
o c˜
sejam y0 e z0 ´ necess´rio e suficiente que
e a
y1 (t0 ) y2 (t0 )
D = det = 0.
y1 (t0 ) y2 (t0 )
˙ ˙
y0 y2 (t0 ) − z0 y2 (t0 )
˙
Neste caso, a solu¸ao do sistema (3.11) ´ c1 =
c˜ e e
D
z0 y1 (t0 ) − y0 y1 (t0 )
˙
c2 = . Assim, provamos o seguinte
D
Teorema 3.3. Sejam y1 (t) e y2 (t) solu¸˜es de [L.H.] tais que
co
y1 (t) y2 (t)
det =0 (3.12)
y1 (t) y2 (t)
˙ ˙
para todo t ∈ I. Ent˜o toda solu¸˜o de [L.H.] ´ dada por (3.10).
a ca e
Observacao 3.3. Em vista do Teorema 3.3, costuma-se dizer que
¸˜
(3.10) ´ a solu¸˜o geral de [L.H.], ou que y1 (t) e y2 (t) constituem
e ca
um conjunto fundamental de solu¸˜es, ou que y1 (t) e y2 (t) s˜o
co a
solu¸oes linearmente independentes de [L.H.].
c˜
Observacao 3.4. O determinante (3.12) desempenha um papel im-
¸˜
portante no estudo da equa¸˜o [L.H.]. Ele ´ chamado Wronskiano
ca e
de y1 (t) e y2 (t) e denotado por W [y1 , y2 ](t), ou simplesmente W (t).
Observacao 3.5. O Teorema 3.3 reduz o problema de obter a solu¸ao
¸˜ c˜
geral de [L.H.] ao problema de encontrar duas solu¸oes convenientes
c˜
y1 e y2 (isto ´, tais que W [y1 , y2 ](t) = 0).
e

46. Eq. Dif. Linear de 2a Ordem
¯ Cap. 3 Teoria Geral 38
Observacao 3.6. Se W [y1 , y2 ](t) ≡ 0 podem existir solu¸oes de
¸˜ c˜
[L.H.] que n˜o sejam dadas por (3.10). Por exemplo, tomando como
a
solu¸oes da equa¸˜o (3.6) y1 (t) = cos ω t e y2 (t) = 5 cos ω t, temos
c˜ ca
W [y1 , y2 ](t) ≡ 0. Notemos que a solu¸ao y(t) = sen ωt n˜o pode ser
c˜ a
escrita como c1 cos ω t + 5c2 cos ω t.
Observacao 3.7. Dadas duas fun¸˜es quaisquer ϕ1 e ϕ2 (que n˜o
¸˜ co a
sejam solu¸˜es de [L.H.]), podem existir valores de t para os quais o
co
wronskiano de ϕ1 e ϕ2 seja nulo e outros valores de t para os quais
o wronskiano n˜o se anule. Por exemplo, se ϕ1 (t) = t e ϕ2 (t) = t2 ,
a
temos
t t2
W (t) = det = t2 .
1 2t
Portanto, W (0) = 0 e W (1) = 1.
O pr´ximo teorema mostra que a situa¸˜o descrita na Observa¸ao
o ca c˜
3.7 n˜o ocorre se ϕ1 e ϕ2 forem solu¸˜es de [L.H.].
a co
Teorema 3.4. Sejam y1 (t), y2 (t), t ∈ I, solu¸˜es de [L.H.] e t0 ∈ I
co
fixado. Seja W (t) o wronskiano de y1 e y2 . Ent˜o
a
t
− a(s) ds
W (t) = W (t0 ) e t0
, para todo t ∈ I. (3.13)
Em particular, como a fun¸˜o exponencial nunca se anula, segue-se
ca
que se W (t0 ) = 0, ent˜o W (t) = 0 para todo t ∈ I.
a
Demonstracao. Temos que
¸˜
W (t) = y1 (t) y2 (t) − y1 (t) y2 (t).
˙ ˙
Derivando, obtemos
˙
W (t) = y1 (t) [−a(t) y2 (t) − b(t) y2 (t)] − y2 (t) [−a(t) y1 (t) − b(t) y1 (t)]
˙ ˙
= −a(t) [y1 (t) y2 (t) − y1 (t) y2 (t)] = −a(t) W (t).
˙ ˙

47. Eq. Dif. Linear de 2a Ordem
¯ Cap. 3 Teoria Geral 39
˙
Portanto, W (t) + a(t) W (t) = 0. Resolvendo esta equa¸ao linear de
c˜
a ordem em W , obtemos (3.13).
1¯
Observe que as conclus˜es de Teorema 3.4 referem-se apenas ao
o
intervalo I no qual as fun¸˜es a(t) e b(t) s˜o cont´
co a ınuas. Para pontos
fora deste intervalo as conclus˜es podem falhar. Veja o exemplo a
o
seguir:
Exemplo 3.1. As fun¸˜es y1 (t) = 1 e y2 (t) = t2 s˜o solu¸˜es da
co a co
1
equa¸ao y − y = 0, para t 0. Temos
c˜ ¨ ˙
t
1 t2
W (t) = det = 2 t.
0 2t
Portanto, W (0) = 0 e W (t) = 0 para todo t 0. Isto n˜o contradiz
a
o Teorema 3.4, uma vez que o coeficiente −1/t n˜o ´ definido para
a e
t = 0. Notemos ainda que a solu¸ao geral desta equa¸˜o ´ c1 + c2 t2 ,
c˜ ca e
visto que W (1) = 2 = 0.
Finalmente, observamos que ´ sempre poss´ obter duas solu¸˜es
e ıvel co
y1 e y2 de [L.H.] tais que W [ y1 , y2 ](t) = 0 para todo t ∈ I. De fato,
fixado t0 ∈ I, basta definir y1 (t) como sendo a unica solu¸˜o de [L.H.]
´ ca
tal que y(t0 ) = 1 e y(t0 ) = 0 e, y2 (t) como sendo a unica solu¸˜o de
˙ ´ ca
[L.H.] tal que y(t0 ) = 0 e y(t0 ) = 1. Assim W (t0 ) = 1 e segue do
˙
Teorema 3.4 que W (t) = 0 para todo t ∈ I. Resumimos estes fatos no
seguinte
Teorema 3.5. Suponhamos que a(t) e b(t) sejam fun¸˜es cont´nuas
co ı
no intervalo I. Ent˜o existem duas solu¸˜es y1 (t) e y2 (t) da equa¸˜o
a co ca
y + a(t) y + b(t) y = 0
¨ ˙
tais que W [ y1 , y2 ](t) = 0, para todo t ∈ I. Al´m disso, a solu¸˜o
e ca
geral desta equa¸˜o ´ dada por c1 y1 (t) + c2 y2 (t), em que c1 e c2 s˜o
ca e a
constantes arbitr´rias.
a

48. Eq. Dif. Linear de 2a Ordem
¯ Cap. 3 Teoria Geral 40
Observacao 3.8. O Teorema 3.5 garante que o espa¸o das solu¸oes
¸˜ c c˜
da equa¸ao [L.H.] ´ um espa¸o vetorial de dimens˜o 2.
c˜ e c a
√
Exerc´ıcios 3.1. 1) a) Mostre que y1 = t e y2 = 1/t s˜o solu¸oes
a c˜
da equa¸ao diferencial 2 t2 y + 3 t y − y = 0, no intervalo 0 t ∞.
c˜ ¨ ˙
b) Calcule W [ y1 , y2 ](t). Que acontece quando t tende a zero?
c) Mostre que y1 (t) e y2 (t) formam um conjunto fundamental de
solu¸oes da equa¸ao dada, no intervalo 0 t ∞.
c˜ c˜
d) Resolva o P.V.I. 2 t2 y + 3 t y − y = 0, y(1) = 2, y(1) = 1.
¨ ˙ ˙
2) Sejam y1 (t) e y2 (t) solu¸oes de y + a(t) y + b(t) y = 0 no intervalo
c˜ ¨ ˙
−∞ t ∞ com y1 (0) = 3, y1 (0) = 1, y2 (0) = −1 e y2 (0) = 1/3.
˙ ˙
Mostre que y1 (t) e y2 (t) s˜o linearmente independentes no intervalo
a
−∞ t ∞.
3) Sejam y1 (t) = t2 e y2 (t) = t |t|.
a) Mostre que y1 e y2 s˜o linearmente dependentes no intervalo [0, 1].
a
b) Mostre que y1 e y2 s˜o linearmente independentes em [−1, 1].
a
c) Mostre que W [ y1 , y2 ] ´ identicamente nulo.
e
d) Mostre que y1 e y2 n˜o podem nunca ser solu¸ao de y + a(t) y +
a c˜ ¨ ˙
b(t) y = 0 no intervalo −1 ≤ t ≤ 1 se ambas as fun¸oes a(t) e b(t)
c˜
forem cont´ınuas neste intervalo.
4) Considere a equa¸˜o y +a(t) y +b(t) y = 0, com a(t) e b(t) cont´
ca ¨ ˙ ınuas
num intervalo I. Mostre que:
a) Se y1 e y2 se anulam no mesmo ponto do intervalo I, ent˜o elas n˜o
a a
podem formar um conjunto fundamental de solu¸˜es em I.
co
b) Se y1 e y2 assumem um m´ximo ou um m´
a ınimo no mesmo ponto do
intervalo I, ent˜o elas n˜o podem formar um conjunto fundamental
a a
de solu¸oes em I.
c˜

49. Eq. Dif. Linear de 2a Ordem
¯ Cap. 3 Redu¸˜o de Ordem
ca 41
c) Se y1 e y2 formam um conjunto fundamental de solu¸˜es, ent˜o elas
co a
n˜o podem ter um ponto de inflex˜o comum em I, a menos que a(t)
a a
e b(t) se anulem simultaneamente a´ı.
3.2 ¸˜
Reducao de Ordem
Suponhamos conhecida uma solu¸ao y1 (t) de [L.H.]. J´ vimos que
c˜ a
para toda constante c ∈ R, c y1 (t) tamb´m ´ solu¸ao de [L.H.]. Este
e e c˜
fato sugere que tentemos encontrar uma outra solu¸˜o de [L.H.] da
ca
forma
y2 (t) = v(t) y1 (t),
em que v(t) ´ uma fun¸˜o n˜o constante. Este procedimento, devido
e ca a
a D’Alembert (1717-1783), ´ usualmente chamado m´todo da
e e
redu¸˜o de ordem. Note que y2 = v y1 implica que
ca
y2 = v y1 + v y˙1
˙ ˙ e y2 = v y1 + 2 v y˙1 + v y1 .
¨ ¨ ˙ ¨
Substituindo em [L.H.], obtemos
v [ y1 + a y1 + b y1 ] + v [ 2y1 + a y1 ] + v y1 = 0.
¨ ˙ ˙ ˙ ¨
Como y1 + a y1 + b y1 = 0 (pois y1 ´ solu¸˜o de [L.H.]), temos que v ´
¨ ˙ e ca e
solu¸ao de:
c˜
2y˙1
v+ a+
¨ v = 0.
˙
y1
Fazendo z = v, temos a equa¸ao de 1a ordem em z
˙ c˜ ¯
2y˙1
z+ a+
˙ z=0
y1
cuja solu¸˜o ´ dada por z(t) = c e−
ca e (a(t)+2[y(t)/y(t)]) dt
˙
= c u(t), em que
c ´ constante. Logo,
e
v(t) = z(t) dt = c u(t) dt

50. Eq. Dif. Linear de 2a Ordem
¯ Cap. 3 Redu¸˜o de Ordem
ca 42
e ent˜o
a
y2 (t) = v(t) y1 (t) = c y1 (t) u(t) dt.
Portanto, as duas solu¸˜es de [L.H.] s˜o y1 (t) e y2 (t) = y1 (t)
co a u(t) dt.
Exemplo 3.2. Determine a 2a solu¸ao da equa¸˜o
¯ c˜ ca
t2 y + 2 t y − 2 y = 0
¨ ˙
sabendo-se que y1 (t) = t.
Solucao: Vamos procurar y2 (t) = v(t) y1 (t) = t v(t). Assim,
¸˜
y2 = v + t v
˙ ˙ e y2 = t v + 2 v.
¨ ¨ ˙
Substituindo na equa¸˜o, obtemos
ca
t2 (t v + 2 v) + 2 t (v + t v) − 2 t v = 0
¨ ˙ ˙
que implica
t3 v + 4 t2 v = 0.
¨ ˙
Fazendo z = v, temos
˙
t3 z + 4 t2 z = 0
˙
que ´ uma E.D.O. linear de 1a ordem em z. Escrevendo
e ¯
4
z+ z=0
˙
t
(4/t) dt
temos que µ(t) = e = t4 . Portanto,
d 4
(t z) = 0.
dt
Logo, t4 z = c. Equivalentemente, z = c t−4 . Logo,
1
v(t) = z(t) dt = t−4 dt = − t−3 .
3
Portanto,
1 1
y2 (t) = − t−3 y1 (t) = − t−2 .
3 3

51. Eq. Dif. Linear de 2a Ordem
¯ Cap. 3 Equa¸˜o homogˆnea. 43
ca e
Exerc´ıcios 3.2. Determine, por redu¸ao de ordem, a 2a solu¸ao das
c˜ ¯ c˜
equa¸oes abaixo:
c˜
1) y − 4 y − 12 y = 0, y1 (t) = e6t .
¨ ˙
2) y − 2 y + y = 0, y1 (t) = et .
¨ ˙
3) t2 y + 2 t y = 0, y1 (t) = 1.
¨ ˙
√
4) 2 t2 y + 3 t y − y = 0, y1 (t) =
¨ ˙ t.
3.3 ¸˜ ˆ
Equacoes Homogeneas com Coefi-
cientes Constantes
Consideremos a equa¸˜o
ca
a y + b y + c y = 0,
¨ ˙ (3.14)
em que a, b e c s˜o constantes reais com a = 0.
a
¨ g
Exemplo 3.3. 1) Movimento de um pˆndulo simples θ + θ = 0.
e
b k
2) Sistema massa mola: y +
¨ y+
˙ y = 0, em que o termo b y
˙
m m
´ devido ` resistˆncia do meio.
e a e
De acordo com o Teorema 3.5, basta encontrar duas solu¸˜es y1 (t)
co
e y2 (t) linearmente independentes (isto ´, W [ y1 , y2 ](t) = 0) de (3.14)
e
e todas as demais ser˜o combina¸oes destas.
a c˜
Observemos que se y = ϕ(t) ´ uma solu¸˜o de (3.14) ent˜o a soma
e ca a
dos termos a ϕ(t), b ϕ(t) e c ϕ(t) deve ser igual a zero para todo t.
¨ ˙
Para que isto ocorra as trˆs fun¸oes ϕ(t), ϕ(t) e ϕ(t) devem ser do
e c˜ ˙ ¨
4
“mesmo tipo”. Por exemplo a fun¸˜o y(t) = t nunca poder´ ser
ca a

52. Eq. Dif. Linear de 2a Ordem
¯ Cap. 3 Equa¸˜o homogˆnea. 44
ca e
solu¸ao de (3.14) pois os termos 12 a t2 , 4 b t3 e c t4 s˜o polinomios de
c˜ a
graus diferentes e, por isso sua soma n˜o se cancela. Por outro lado,
a
a fun¸ao y(t) = eλt , em que λ ´ constante, tem a propriedade de que
c˜ e
tanto y(t) como y (t) s˜o m´ltiplos de y(t). Isto sugere que tentemos
˙ ¨ a u
y(t) = e como solu¸˜o de (3.14). Substituindo y(t) = eλt em (3.14)
λt
ca
obtemos
a (eλt ) + b (eλt ) + c eλt = 0 =⇒ eλt (a λ2 + b λ + c) = 0
o que implica que
a λ2 + b λ + c = 0. (3.15)
Portanto, y(t) = eλt ´ uma solu¸ao de (3.14) se, e somente, se λ ´ raiz
e c˜ e
de (3.15). A equa¸ao (3.15) ´ chamada Equa¸˜o Caracter´
c˜ e ca ıstica de
(3.14). As ra´ de (3.15) s˜o
ızes a
√ √
−b + b2 − 4 a c −b − b2 − 4 a c
λ1 = e λ2 = .
2a 2a
Vamos analisar as trˆs possibilidades para o discriminante b2 −4 a c:
e
i) b2 − 4 a c 0: Ra´
ızes reais distintas
Neste caso eλ1 t e eλ2 t s˜o solu¸oes de (3.14) e seu wronskiano
a c˜
eλ1 t eλ2 t
W (t) = det = (λ2 − λ1 )e(λ1 +λ2 )t = 0,
λ1 eλ1 t λ2 eλ2 t
para todo t ∈ R. Logo, as solu¸oes s˜o linearmente independentes e,
c˜ a
portanto, formam uma base do espa¸o das solu¸oes. Ou seja, qualquer
c c˜
solu¸ao de (3.14) ´ da forma
c˜ e
y(t) = c1 eλ1 t + c2 eλ2 t .
ii) b2 − 4 a c = 0: Ra´
ızes reais iguais
b
Neste caso λ1 = λ2 = − e com isto temos uma solu¸˜o y1 =
ca
2a
(−b/2 a) t
e . Vamos encontrar a outra solu¸˜o de (3.14) (n˜o m´ltipla de
ca a u

53. Eq. Dif. Linear de 2a Ordem
¯ Cap. 3 Equa¸˜o homogˆnea. 45
ca e
y1 ) usando redu¸˜o de ordem, isto ´, procurando v(t) n˜o constante
ca e a
−(b/2 a) t
tal que y2 (t) = v(t) e seja solu¸˜o de (3.14). Substituindo em
ca
(3.14), obtemos
b2 b2
e−(b/2 a) t a v +
¨ − + c v = 0.
4a 2a
Como e−(b/2 a) t = 0 para todo t e b2 − 4 a c = 0, temos
v = 0 =⇒ v(t) = α t + β, com α, β ∈ R.
¨
Podemos tomar α = 1 e β = 0, pois queremos encontrar uma solu¸˜o.
ca
Logo, v(t) = t. Portanto, a outra solu¸˜o de (3.14) ´
ca e
y2 (t) = t e−(b/2 a) t .
Exemplo 3.4. Resolva o P.V.I.
y + 6y + 9y = 0
¨ ˙
y(0) = 1, y(0) = 2.
˙
Solucao: y = eλt =⇒ λ2 + 6 λ + 9 = 0 =⇒ λ1 = λ2 = −3. Portanto,
¸˜
a solu¸ao geral ´
c˜ e
y(t) = (c1 + c2 t) e−3 t .
Como y(0) = 1, temos c1 = 1. Al´m disso, y(t) = (c2 − 3 − 3 c2 t) e−3 t
e ˙
e y(0) = 2. Logo, c2 = 5. Portanto, a solu¸ao do P.V.I. ´
˙ c˜ e
y(t) = e−3 t + 5 t e−3 t .
iii) b2 − 4 a c 0: Ra´
ızes Complexas
Logo,
√ √
b i 4 a c − b2 b i 4 a c − b2
λ1 = − + e λ2 = − − .
2a 2a 2a 2a

54. Eq. Dif. Linear de 2a Ordem
¯ Cap. 3 Equa¸˜o homogˆnea. 46
ca e
ıamos de dizer que eλ1 t e eλ2 t s˜o solu¸˜es de (3.14). Entretanto
Gostar´ a co
surgem dois problemas:
a) definir eλ t para λ complexo,
b) mesmo que consigamos definir eλ1 t e eλ2 t como solu¸˜es (que
co
certamente ter˜o valores complexos) de (3.14) queremos obter solu¸˜es
a co
reais.
Comecemos resolvendo o segundo problema, pois caso contr´rio
a
n˜o teria sentido resolver o primeiro.
a
¸˜ ˙
Definicao 3.1. Se F (t) = u(t)+i v(t), definimos F (t) = u(t)+i v(t).
˙ ˙
Observacao 3.9. Esta defini¸˜o faz sentido, pois podemos identi-
¸˜ ca
ficar F (t) = u(t) + i v(t) com f (t) = (u(t), v(t)). Logo, f (t) ´ uma
e
parametriza¸ao de uma curva plana cujo vetor velocidade ´ (u(t), v(t)).
c˜ e ˙ ˙
Fica ent˜o natural a defini¸ao acima.
a c˜
Proposicao 3.1. Se y(t) = u(t) + i v(t) ´ uma solu¸˜o a valores
¸˜ e ca
complexos de (3.14), ent˜o u(t) e v(t) s˜o solu¸˜es reais de (3.14).
a a co
Demonstracao. Note que
¸˜
a y (t) + b y(t) + c y(t) = 0
¨ ˙
ou seja,
[a u(t) + b u(t) + c u(t)] + i [a v (t) + b v(t) + c v(t)] = 0.
¨ ˙ ¨ ˙
Para que um n´mero complexo seja zero ´ necess´rio que sua parte
u e a
real e sua parte imagin´ria sejam zero. Logo,
a
a u(t) + b u(t) + c u(t) = 0 e a v (t) + b v(t) + c v(t) = 0.
¨ ˙ ¨ ˙
Isto ´ u e v s˜o solu¸oes (3.14).
e a c˜
E com isto resolvemos o segundo problema. Passemos agora ao
´
primeiro, isto ´, vamos definir eλ t para λ complexo. E natural pedir
e

55. Eq. Dif. Linear de 2a Ordem
¯ Cap. 3 Equa¸˜o homogˆnea. 47
ca e
que esta fun¸ao satisfa¸a ea+b = ea eb . Logo, se λ = α + i β, devemos
c˜ c
ter
eλ t = eα t+i β t = eα t ei β t .
Portanto, basta apenas definirmos ei β t .
Sabemos que, para todo x real, vale
∞
x xn x2 x3
e = =1+x+ + + ··· .
n=0
n! 2! 3!
A equa¸ao acima tem sentido, formalmente, mesmo para x complexo.
c˜
Isto sugere que coloquemos
(i θ)2 (i θ)3
ei θ = 1 + i θ + + + ··· =
2! 3!
θ2 i θ3 θ4 i θ5
= 1 + iθ − − + + − ···
2! 3! 4! 5!
θ2 θ4 θ3 θ5
= 1− + − ··· + i θ − + − ··· ,
2! 4! 3! 5!
θ2 θ4 θ3 θ5
Como cos θ = 1 − 2!
+ 4!
− · · · e sen θ = θ − 3!
+ 5!
− · · · ´ razo´vel
e a
definir
ei θ = cos θ + i sen θ.
Portanto,
eλ t = e(α+i β) t = eα t (cos β t + i sen β t).
deλ t
ıcio: Mostre que
Exerc´ = λ eλ t para λ complexo.
dt
Agora ´ f´cil verificar que
e a
√
λt αt −b 4 a c − b2
y(t) = e =e (cos β t + i sen β t), com α = e β=
2a 2a
´ uma solu¸ao a valores complexos de (3.14), se b2 − 4 a c 0. Logo,
e c˜
pela Proposi¸˜o 3.1, temos que
ca
y1 (t) = eα t cos β t e y2 (t) = eα t sen β t

56. Eq. Dif. Linear de 2a Ordem
¯ Cap. 3 Equa¸˜o homogˆnea. 48
ca e
s˜o duas solu¸oes reais de (3.14).
a c˜
ıcio: Mostre que W [ y1 , y2 ](t) = βe2 α t .
Exerc´
Pelo exerc´ acima, temos que y1 (t) = eα t cos β t e y2 (t) = eα t sen β t
ıcio
formam uma base do espa¸o solu¸ao e, conseq¨entemente, a solu¸ao
c c˜ u c˜
2
geral de (3.14) para b − 4 a c 0 ´
e
y(t) = eα t (c1 cos β t + c2 sen β t).
¸˜ ¯
Observacao 3.10. Pode-se pensar que eλ2 t , em que λ2 = λ1 dar´a
origem a outras duas solu¸oes. Todavia, isto n˜o ocorre, pois
c˜ a
eλ2 t = e(α−i β) t = eα t [cos(−β t) + i sen(−βt)] = eα t [cos βt − sen β t].
Portanto,
y1 (t) = [eλ2 t ] = eα t cos β t = y1 (t)
˜
e
y2 (t) = [eλ2 t ] = −eα t sen β t = −y2 (t).
˜
Exemplo 3.5. Determine a solu¸˜o real do P.V.I.
ca
y + 2y + 5y = 0
¨ ˙
y(0) = 1, y(0) = 3.
˙
Solucao: A equa¸ao caracter´
¸˜ c˜ ıstica λ2 + 2 λ + 5 = 0 possui ra´
ızes
complexas λ1 = −1 + 2 i e λ2 = −1 − 2 i. Portanto,
eλ1 t = e(−1+2 i) t = e−t cos 2 t + i e−t sen 2 t
´ uma solu¸˜o com valores complexos de y + 2 y + 5 y = 0. Logo, pela
e ca ¨ ˙
Proposi¸ao 3.1, temos que
c˜
y1 (t) = (eλ1 t ) = e−t cos 2 t e y2 (t) = (eλ1 t ) = e−t sen 2 t
s˜o solu¸˜es reais da equa¸˜o. Mais ainda, elas formam uma base para
a co ca
o espa¸o solu¸˜o. Portanto, a solu¸ao geral ´
c ca c˜ e
y(t) = e−t (c1 cos 2 t + c2 sen 2 t),

57. Eq. Dif. Linear de 2a Ordem
¯ Cap. 3 Equa¸˜o homogˆnea. 49
ca e
onde c1 e c2 s˜o constantes reais. Como y(0) = 1, temos c1 = 1. Logo,
a
y(t) = e (cos 2 t + c2 sen 2 t). Isso implica que y(t) = −e−t (cos 2 t +
−t
˙
c2 sen 2 t) + e−t (−2 sen 2 t + 2 c2 cos 2 t). Portanto, y(0) = 3 implica
˙
que c2 = 2. Logo, a solu¸˜o do P.V.I. ´
ca e
y(t) = e−t (cos 2 t + 2 sen 2 t).
Exemplo 3.6. (Vibra¸˜es livres n˜o amortecidas) Consideremos
co a
o sistema massa-mola enunciado no Cap´
ıtulo 1, Subse¸ao 1.1.3, cuja
c˜
equa¸ao ´
c˜ e
my + ky = 0
¨
ou
y + ω 2 y = 0,
¨
em que ω = k/m (lembremos que k 0 e m 0).
A equa¸ao caracter´
c˜ ıstica λ2 + ω 2 = 0 possui ra´ızes complexas
λ1 = i ω e λ2 = −i ω. Logo, ϕ(t) = ei ω t = cos ω t + i sen ω t ´ uma
e
solu¸ao com valores complexos que d´ origem as seguintes solu¸˜es
c˜ a ` co
reais linearmente independentes
y1 (t) = cos ω t e y2 (t) = sen ω t.
Portanto, a solu¸ao geral ´ dada por
c˜ e
y(t) = c1 cos ω t + c2 sen ω t.
Observacao 3.11. Para esbo¸ar o gr´fico de y(t), vamos reescrevˆ-la
¸˜ c a e
de modo mais apropriado: denotando A = c2 + c2 e α = arctg(c2 /c1 ),
1 2
podemos escrever
y(t) = c1 cos ω0 t + c2 sen ω0 t = A cos(ω0 t − α),
Logo, temos que y(t) est´ sempre entre −A e +A e, portanto, o movi-
a
mento ´ peri´dico de per´
e o ıodo 2π/ω0 , amplitude A, freq¨ˆncia ω0 e
ue
angulo de fase α. O gr´fico de y(t) ´ mostrado na figura abaixo.
ˆ a e

58. Eq. Dif. Linear de 2a Ordem
¯ Cap. 3 Equa¸˜o homogˆnea. 50
ca e
y T
2π/ω0
A
t
E
−A
Este movimento tamb´m ´ chamado de movimento harmˆnico
e e o
simples.
Exemplo 3.7. (Vibra¸oes livres amortecidas) Consideremos o sis-
c˜
tema massa-mola, supondo agora que o meio oferece uma for¸a de c
resistˆncia proporcional ` velocidade do corpo. Portanto, devemos
e a
resolver a equa¸ao
c˜
c k
y+
¨ y+
˙ y = 0.
m m
A equa¸˜o caracter´ √ ´ m λ2 + c λ + k = √ cujas ra´
ca ıstica e 0, ızes s˜o:
a
−c + c 2 − 4mk −c − c 2 − 4mk
λ1 = e λ2 = .
2m 2m
Consideremos as seguintes situa¸˜es:
co
ıtico ou forte (c2 − 4 m k 0)
(i) amortecimento supercr´
Neste caso temos que λ1 e λ2 y T
s˜o reais e negativas. De fato,
√a
c2 − 4 m k c. A solu¸˜o geral
ca
´:
e
t
y(t) = c1 eλ1 t + c2 eλ2 t .
E
casos (i) e (ii)

59. Eq. Dif. Linear de 2a Ordem
¯ Cap. 3 Equa¸˜o homogˆnea. 51
ca e
ıtico (c2 − 4 m k = 0)
(ii) amortecimento cr´
y
Como c2 − 4 m k = 0, temos que
T
λ1 = λ2 = −c/(2 m).
Neste caso, a solu¸ao geral ´:
c˜ e t
E
y(t) = (c1 + c2 t) e−c t/(2 m) .
casos (i) e (ii)
ıtico ou oscilat´rio (c2 − 4 m k 0)
(iii) amortecimento subcr´ o
Como c2 − 4 m k 0, temos que λ1 e λ2 s˜o complexos conjugados.
a
Portanto, a solu¸ao geral ´:
c˜ e
y(t) = e(−c/2 m)t (c1 cos µ t + c2 sen µ t),
√
4 m k − c2
em que µ = ou y(t) = A e(−c/2 m) t cos(µ t − α). Logo, a
2m
solu¸ao oscila entre duas curvas y = −A e(−c/2 m) t e y = A e(−c/2 m) t .
c˜
Portanto, representa a curva do cosseno com amplitude decrescente.
y T
y = A e−c t/2 m
)
t
E
T
y = −A e−c t/2 m
Nos trˆs casos o movimento se “extingue” no futuro se existe atrito
e
no sistema, ou seja, qualquer perturba¸˜o inicial ´ dissipada pelo atrito
ca e
existente. Esta ´ uma das raz˜es pelas quais os sistemas massa-mola
e o

60. Eq. Dif. Linear de 2a Ordem
¯ Cap. 3 Eq. N˜o Homogˆnea 52
a e
s˜o uteis nos sistemas mecˆnicos; eles podem ser usados para amorte-
a ´ a
cer qualquer perturba¸˜o indesejada.
ca
ıcios 3.3. 1) Determine a solu¸ao geral de:
Exerc´ c˜
a) y − y − 2 y = 0.
¨ ˙ b) y − 7 y = 0.
¨ ˙ c) y + 4 y = 0.
¨
d) y − 4 y + 13 y = 0. e) y − 4 y + 4 y = 0. f) y = 0.
¨ ˙ ¨ ˙ ¨
2) a) Seja λ1 = α + i β uma raiz complexa de λ2 + (a − 1) λ + b = 0.
Mostre que
tα+iβ = tα ti β = tα e(ln t) i β = tα [cos(β ln t) + i sen(β ln t)]
´ uma solu¸ao com valores complexos da equa¸˜o de Euler
e c˜ ca
t2 y + a t y + b y = 0.
¨ ˙ (3.16)
b) Mostre que tα cos(β ln t) e tα sen(β ln t) s˜o solu¸˜es reais de (3.16).
a co
3) Determine a solu¸ao geral de:
c˜
a) t2 y +t y+y = 0,
¨ ˙ t 0. b) t2 y +2 t y+2 y = 0,
¨ ˙ t 0.
3.4 ¸˜ ˜ ˆ
A Equacao Nao Homogenea
Consideremos a equa¸˜o n˜o homogˆnea
ca a e
y + a(t) y + b(t) y = g(t),
¨ ˙ [L.N.H.]
em que a(t), b(t) e g(t) s˜o fun¸˜es cont´
a co ınuas em um intervalo I e
g(t) = 0.
Nos fenˆmenos f´
o ısicos descritos por equa¸˜o da forma acima, o
ca
termo g(t) representa, em geral, um “agente externo” atuando sobre

61. Eq. Dif. Linear de 2a Ordem
¯ Cap. 3 Eq. N˜o Homogˆnea 53
a e
o sistema. Por exemplo, o sistema massa-mola, sujeito apenas ` a¸˜o
a ca
k
da gravidade, ´ descrito pela equa¸˜o: y +
e ca ¨ y = 0. Agora, se im-
m
pusermos ao sistema acima uma for¸a externa peri´dica de intensidade
c o
k A
A cos ωt, a equa¸˜o fica y + y =
ca ¨ cos ω t.
m m
Um fato que foi observado para a equa¸ao linear de 1a ordem n˜o
c˜ ¯ a
homogˆnea y + α(t) y = β(t) (ver Observa¸ao 2.4) ´ que sua solu¸ao
e ˙ c˜ e c˜
geral ´ const´
e ıtuida de duas parcelas:
i) a solu¸˜o geral da homogˆnea y + α(t) y = 0;
ca e ˙
ii) uma solu¸ao particular da equa¸˜o n˜o homogˆnea y+α(t) y = β(t).
c˜ ca a e ˙
Mostraremos que este fato tamb´m ´ verdadeiro para as equa¸oes
e e c˜
a ordem (na verdade, ´ v´lida em geral).
lineares de 2¯ e a
Teorema 3.6. Sejam y1 (t) e y2 (t) solu¸˜es linearmente independentes
co
da equa¸˜o homogˆnea
ca e
y + a(t) y + b(t) y = 0,
¨ ˙ [L.H.]
e seja ϕ(t) uma solu¸˜o particular da equa¸˜o n˜o homogˆnea [L.N.H.].
ca ca a e
Ent˜o toda solu¸˜o y(t) de [L.N.H.] ´ da forma
a ca e
y(t) = c1 y1 (t) + c2 y2 (t) + ϕ(t), (3.17)
para alguma escolha conveniente das constantes c1 e c2 .
¸˜ ´ a
Demonstracao. E f´cil mostrar que se ϕ1 e ϕ2 s˜o solu¸oes
a c˜
de [L.N.H.], ent˜o a fun¸˜o ψ(t) = ϕ1 (t) − ϕ2 (t) ´ solu¸ao de [L.H.]
a ca e c˜
(Exerc´
ıcio).
Seja agora y(t) uma solu¸ao qualquer de [L.N.H.]. Pela parte an-
c˜
terior a fun¸ao w(t) = y(t) − ϕ(t) ´ solu¸˜o de [L.H.]. Por´m, toda
c˜ e ca e
solu¸ao de [L.H.] ´ combina¸˜o linear de y1 (t) e y2 (t). Ent˜o
c˜ e ca a
y(t) − ϕ(t) = c1 y1 (t) + c2 y2 (t).
Logo, y(t) = c1 y1 (t) + c2 y2 (t) + ϕ(t).

62. Eq. Dif. Linear de 2a Ordem
¯ Cap. 3 Eq. N˜o Homogˆnea 54
a e
Observacao 3.12. A grande utilidade do Teorema 3.6 ´ que ele reduz
¸˜ e
o problema de encontrar todas as solu¸oes de [L.N.H.] ao problema
c˜
mais simples de encontrar duas solu¸oes linearmente independentes
c˜
de [L.H.] e uma solu¸ao de [L.N.H.].
c˜
Observacao 3.13. A express˜o (3.17) ´ chamada solu¸˜o geral de
¸˜ a e ca
[L.N.H.].
Exemplo 3.8. Determine a solu¸˜o geral de y + y = t.
ca ¨
Solucao: Vamos determinar a solu¸ao geral da homogˆnea associ-
¸˜ c˜ e
ada: y + y = 0. A equa¸ao caracter´
¨ c˜ ıstica λ2 + 1 = 0 possui ra´
ızes
it
complexas λ = ±i. Logo ψ(t) = e = cos t + i sen t ´ uma solu¸ao
e c˜
a valores complexos. Ent˜o y1 (t) = cos t e y2 (t) = sen t s˜o duas
a a
solu¸oes reais linearmente independentes de y + y = 0. Al´m disso,
c˜ ¨ e
ϕ(t) = t ´ obviamente uma solu¸ao particular de y + y = t. Logo, pelo
e c˜ ¨
Teorema 3.6, toda solu¸˜o desta equa¸ao ´ da forma
ca c˜ e
y(t) = c1 cos t + c2 sen t + t.
Exemplo 3.9. Trˆs solu¸oes de uma equa¸ao linear n˜o homogˆnea de
e c˜ c˜ a e
a ordem s˜o: ϕ (t) = t, ϕ (t) = t + et e ϕ (t) = 1 + t + et . Determine
2¯ a 1 2 3
a solu¸ao geral desta equa¸˜o.
c˜ ca
Solucao: As fun¸oes ϕ2 (t) − ϕ1 (t) = et e ϕ3 (t) − ϕ2 (t) = 1 s˜o
¸˜ c˜ a
t
solu¸oes da homogˆnea associada e, al´m disso, as fun¸˜es e e 1 s˜o
c˜ e e co a
linearmente independentes. Logo, a solu¸˜o geral de tal equa¸ao ´:
ca c˜ e
y(t) = c1 + c2 et + t.
Exerc´ ıcios: Sabendo que ϕ1 , ϕ2 e ϕ3 s˜o solu¸˜es de uma equa¸˜o
a co ca
linear n˜o homogˆnea de 2¯
a e a ordem, determinar a solu¸˜o geral desta
ca
equa¸ao, sendo:
c˜
a) ϕ1 (t) = t2 , ϕ2 (t) = t2 + e2 t e ϕ3 (t) = 1 + t2 + 2 e2 t .
2 2
b) ϕ1 (t) = 1 + et , ϕ2 (t) = 1 + t + et e ϕ3 (t) = (t + 1) et + 1.

63. Eq. Dif. Linear de 2a Ordem
¯ Cap. 3 Eq. N˜o Homogˆnea 55
a e
Para resolvermos uma equa¸ao linear n˜o homogˆnea precisamos
c˜ a e
saber encontrar uma solu¸˜o particular. Veremos agora dois m´todos
ca e
para determinar tal solu¸ao.
c˜
3.4.1 ´
Metodo dos Coeficientes a Determinar
Vamos estudar a equa¸ao
c˜
a y + b y + c y = g(t),
¨ ˙ (3.18)
em que a, b e c s˜o constantes reais e g(t) ´ uma fun¸˜o exponencial,
a e ca
ou um polinˆmio, ou sen t ou cos t. Para estes tipos de fun¸oes g, de-
o c˜
terminaremos facilmente uma solu¸˜o particular. O m´todo tamb´m
ca e e
se aplica a produtos de tais fun¸oes, ou seja
c˜
g(t) = eαt (a0 + a1 t + · · · + an tn ) (b1 sen β t + b2 cos β t).
Antes de discutir um procedimento geral, vamos considerar alguns
exemplos:
Exemplo 3.10. Encontre uma solu¸ao particular da equa¸ao
c˜ c˜
y − 3 y − 4 y = 2 sen t.
¨ ˙
Solucao: Queremos uma fun¸ao yp (t) tal que a soma de sua 2a
¸˜ c˜ ¯
derivada menos 3 vezes a sua 1a derivada menos 4 vezes a pr´pria
¯ o
fun¸ao seja igual a 2 sen t. H´ pouca chance de sucesso se tentar-
c˜ a
mos fun¸˜es como ln t, et ou t2 , pois n˜o importa como combinamos
co a
estas fun¸oes ´ imposs´
c˜ e ıvel obter 2 sen t. Parece obvio que devemos
´
considerar para yp fun¸oes como sen t e cos t. Vamos ent˜o tentar
c˜ a
yp (t) = A cos t + B sen t, em que A e B s˜o constantes a serem deter-
a
minadas. Logo,
yp (t) = −A sen t + B cos t =⇒ yp (t) = −A cos t − B sen t
˙ ¨
e, substituindo na equa¸ao, obtemos
c˜
(−5 A − 3 B) cos t + (3 A − 5 B) sen t = 2 sen t.

64. Eq. Dif. Linear de 2a Ordem
¯ Cap. 3 Eq. N˜o Homogˆnea 56
a e
Esta equa¸ao estar´ identicamente satisfeita se e somente se
c˜ a
−5 A − 3 B = 0 3 5
=⇒ A = e B=− .
3A − 5B = 2 17 17
Logo, uma solu¸˜o particular da equa¸˜o ´:
ca ca e
3 5
yp (t) = cos t − sen t.
17 17
Exemplo 3.11. Idem para y − 3 y − 4 y = 4 t2 .
¨ ˙
¸˜ ´
Solucao : E natural tentar yp (t) = A t2 , em que A ´ uma constante
e
a ser determinada. Ent˜o, yp (t) = 2 A t. Logo, yp (t) = 2 A. Substi-
a ˙ ¨
tuindo na equa¸˜o, obtemos
ca
2 A − 6 A t − 4 A t2 = 4 t2 =⇒ A = 0 e A = −1.
Portanto, ´ imposs´ achar uma solu¸ao da forma A t2 . Entretanto,
e ıvel c˜
pensando no termo 4 t2 como 4 t2 +0 t+0, agora parece razo´vel tentar
a
2
yp (t) = A t +B t+C, em que A, B e C devem ser determinadas. Ent˜o a
yp (t) = 2 A t + B
˙ e yp (t) = 2 A.
¨
Portanto, −4 A t2 + (−6 A − 4 B) t + (2 A − 3 B − 4C) = 4 t2 . Ou seja,
A = −1, B = 3/2 e C = −13/8. Logo,
3 13
yp (t) = −t2 + t− .
2 8
Exemplo 3.12. Idem para y − 3 y − 4 y = e5 t .
¨ ˙
Solucao: Vamos tentar yp (t) = A e5 t . Portanto, yp (t) = 5 A e5 t e
¸˜ ˙
yp (t) = 25 A e5 t . Substituindo na equa¸ao, temos que 6 A e5 t = e5 t .
¨ c˜
1
Ou seja A = . Portanto,
6
1 5t
yp (t) = e .
6

65. Eq. Dif. Linear de 2a Ordem
¯ Cap. 3 Eq. N˜o Homogˆnea 57
a e
Exemplo 3.13. Idem para y − 3 y − 4 y = e−t .
¨ ˙
Solucao: Seria natural tentar yp (t) = A e−t . Portanto, yp (t) =
¸˜ ˙
−A e e yp (t) = A e . Substituindo na equa¸ao, temos 0·A e = e−t
−t
¨ −t
c˜ −t
o que implica que ´ imposs´ determinar A tal que A e−t seja solu¸˜o
e ıvel ca
−t
desta equa¸ao. A dificuldade neste caso ´ que e ´ uma solu¸˜o da
c˜ e e ca
−t
equa¸ao homogˆnea associada e, portanto, A e tamb´m ´ solu¸˜o
c˜ e e e ca
da equa¸ao homogˆnea. Abaixo veremos como resolver esta equa¸ao,
c˜ e c˜
t e−t
cuja yp (t) = − .
5
Passemos ao estudo do caso geral em que g possui uma das formas:
a) Pn (t) = an tn + an−1 tn−1 + · · · + a1 t + a0 ,
b) eαt Pn (t),
c) eαt Pn (t) sen β t ou eαt Pn (t) cos β t,
d) combina¸oes lineares das anteriores.
c˜
1o caso: Se g(t) = Pn (t), an = 0, ent˜o a equa¸ao (3.18) torna-se
¯ a c˜
a y + b y + c y = an tn + an−1 tn−1 + · · · + a1 t + a0 .
¨ ˙ (3.19)
Devemos procurar yp (t) de tal forma que a combina¸ao a yp +b y˙p +
c˜ ¨
c yp seja um polinˆmio de grau n. O candidato natural ´:
o e
yp (t) = An tn + An−1 tn−1 + · · · + A1 t + A0
com os coeficientes A0 , A1 , . . ., An a serem determinados. Substi-
tuindo na equa¸˜o (3.19), temos:
ca
a [n (n − 1) An tn−2 + (n − 1)(n − 2) An−1 tn−3 + · · · + 6 A3 t + 2 A2 ]
+ b [n An tn−1 + (n − 1) An−1 tn−2 + · · · + 2 A2 t + A1 ]
(3.20)
+ c [An tn + An−1 tn−1 + · · · + A1 t + A0 ]
= an tn + an−1 tn−1 + · · · + a1 t + a0 .

66. Eq. Dif. Linear de 2a Ordem
¯ Cap. 3 Eq. N˜o Homogˆnea 58
a e
Igualando os coeficientes, obtemos


 c An = an
c An−1 + n b An = an−1




c An−2 + (n − 1) b An−1 + n (n − 1) a An = an−2 (3.21)
 .
.



 .
 c A0 + b A1 + 2 a A2 = a0 .
Se c = 0, determinamos, pela primeira equa¸ao de (3.21), que
c˜
an
An = . Em seguida, substituimos An na segunda equa¸ao, obtemos
c˜
c
an−1 − (n b an )/c
An−1 = e assim sucessivamente.
c
Se c = 0 e b = 0, ent˜o a yp + b yp ´ um polinˆmio de grau n − 1,
a ¨ ˙ e o
enquanto que Pn (t) ´ um polinˆmio de grau n. Assim, ´ imposs´
e o e ıvel
resolver (3.21). Para garantir que a yp + b yp seja um polinˆmio de
¨ ˙ o
grau n, devemos escolher yp como sendo um polinˆmio de grau n + 1.
o
Portanto, assumimos
yp (t) = t (An tn + · · · + A1 t + A0 )
(omitimos o termo constante pois y = constante ´ uma solu¸ao da
e c˜
equa¸ao homogˆnea a y + b y = 0) e procedemos como anteriormente.
c˜ e ¨ ˙
Se b = c = 0, ent˜o tomamos yp (t) = t2 (An tn + · · · + A1 t + A0 ).
a
2o caso: Consideremos a equa¸˜o diferencial:
¯ ca
a y + b y + c y = eα t Pn (t).
¨ ˙ (3.22)
Se removermos o fator eαt do segundo membro de (3.22), esta equa¸ao c˜
torna-se igual a equa¸ao (3.19). Para conseguirmos isto pomos y =
` c˜
eα t v. Ent˜o y = eα t (v + α v) e y = eαt (¨ + 2 α v + α2 v). Substituindo
a ˙ ˙ ¨ v ˙
na equa¸ao (3.22) e cancelando o fator comum eα t , obtemos
c˜
a v + (2 a α + b)v + (a α2 + b α + c) v = Pn (t).
¨ ˙ (3.23)

67. Eq. Dif. Linear de 2a Ordem
¯ Cap. 3 Eq. N˜o Homogˆnea 59
a e
Conseq¨entemente, y(t) = eα t v(t) ´ solu¸ao de (3.22) se e somente se
u e c˜
v(t) ´ solu¸ao de (3.23), que ´ um problema j´ resolvido.
e c˜ e a
Para encontrar uma solu¸˜o particular v(t) de (3.23), devemos dis-
ca
tinguir os seguintes casos:
(i) a α2 + b α + c = 0,
(ii) a α2 + b α + c = 0, mas 2 a α + b = 0,
(iii) a α2 + b α + c = 2 a α + b = 0.
O caso (i) significa que α n˜o ´ raiz da equa¸ao caracter´
a e c˜ ıstica
a λ2 + b λ + c = 0, (3.24)
ou seja, eα t n˜o ´ solu¸ao da equa¸ao homogˆnea a y + b y + c y = 0.
a e c˜ c˜ e ¨ ˙
Neste caso, temos que yp (t) = Qn (t) e , em que Qn (t) = An tn + · · · +
αt
A1 t + A0 .
A condi¸˜o (ii) significa que α ´ raiz simples da equa¸ao carac-
ca e c˜
ıstica (3.24), ou seja eα t ´ solu¸˜o da equa¸˜o homogˆnea, mas
ter´ e ca ca e
αt αt
t e n˜o ´. Neste caso, yp (t) = t Qn (t) e .
a e
Finalmente, a condi¸ao (iii) significa que tanto eα t como t eα t s˜o
c˜ a
2 αt
solu¸oes da equa¸ao homogˆnea e, portanto, yp (t) = t Qn (t) e .
c˜ c˜ e
Exemplo 3.14. Encontre uma solu¸ao particular da equa¸ao
c˜ c˜
y − 3 y + 2 y = (4 − 6 t) e−t .
¨ ˙
Solucao: A equa¸˜o caracter´
¸˜ ca ıstica λ2 −3 λ+2 = 0 possui duas ra´ ızes
distintas λ1 = 1 e λ2 = 2. Portanto, y1 (t) = et e y2 (t) = e2 t formam
uma base de espa¸o solu¸ao da equa¸ao homogˆnea. Logo, e−t n˜o
c c˜ c˜ e a
´ solu¸˜o da homogˆnea. Portanto, fazemos yp (t) = (A + B t) e−t e
e ca e
temos que
yp (t) = (A + B − B t) e−t
˙ e yp (t) = (A − 2 B + B t)e−t .
¨

68. Eq. Dif. Linear de 2a Ordem
¯ Cap. 3 Eq. N˜o Homogˆnea 60
a e
Substituindo na equa¸˜o e cancelando o fator e−t , obtemos
ca
6A − 5B = 4 A = −1
6 A − 5 B + 3 B t = 4 − 6 t =⇒ =⇒
3B = −6 B = −2.
Logo, yp (t) = −(1 + 2 t) e−t ´ uma solu¸ao.
e c˜
Exemplo 3.15. Idem para y − 3 y + 2 y = (1 + t) et .
¨ ˙
Solucao: Como vimos, no Exemplo 3.14, et ´ solu¸ao da equa¸ao
¸˜ e c˜ c˜
homogˆnea associada. Assim, devemos tentar yp (t) = t (A + B t) et .
e
Isso implica que
yp (t) = [A+(A+2 B) t+B t2 ] et e yp (t) = [2A+2 B+(A+4 B) t+B t2 ] et .
˙ ¨
Substituindo na equa¸˜o e cancelando o fator et , obtemos
ca
−A + 2 B = 1 1
−A+2 B−2 B t = 1+t =⇒ =⇒ A = −2 e B = − .
−2 B = 1 2
Logo, yp (t) = (−2 t − t2 /2) et .
Exemplo 3.16. Encontrar uma solu¸ao particular para a equa¸ao
c˜ c˜
2 3 5 3t
y − 6 y + 9 y = (6 + 12 t + 12 t + 40 t + 42 t ) e .
¨ ˙
Solucao: A equa¸˜o caracter´
¸˜ ca ıstica λ2 − 6 λ + 9 = 0 possui ra´ızes
3t 3t
iguais λ1 = λ2 = 3. Portanto, y1 (t) = e e y2 (t) = t e s˜o solu¸oes
a c˜
da equa¸˜o homogˆnea associada. Logo, a solu¸ao particular da n˜o
ca e c˜ a
homogˆnea ´ da forma
e e
yp (t) = t2 (A0 + A1 t + A2 t2 + A3 t3 + A4 t4 + A5 t5 ) e3 t .
Como se pode notar ´ bem trabalhoso esta express˜o na equa¸ao dada
e a c˜
´ muito mais pr´tico fazer y(t) = e3 t v. Isso
para obter os coeficientes. E a
implica que y = (v + 3 v) e3 t e y = (¨ + 6 v + 9 v) e3 t . Substituindo na
˙ ˙ ¨ v ˙
equa¸ao e cancelando o fator e3 t , obtemos
c˜
v = 6 + 12 t + 12 t2 + 40 t3 + 42 t5 .
¨

69. Eq. Dif. Linear de 2a Ordem
¯ Cap. 3 Eq. N˜o Homogˆnea 61
a e
Integrando duas vezes, vem
v(t) = 3 t2 + 2 t3 + t4 + 2 t5 + t7 .
Logo, uma solu¸˜o particular ´
ca e
yp = (3 t2 + 2 t3 + t4 + 2 t5 + t7 ) e3 t .
3o caso: Consideremos agora a equa¸ao diferencial
¯ c˜
a y + b y + c y = eα t Pn (t) sen βt
¨ ˙ (ou cos β t). (3.25)
Este problema pode ser reduzido ao anterior se notarmos que:
(i) ei β t = cos β t + i sen β t e
(ii) se y(t) = u(t) + i v(t) ´ uma solu¸˜o com valores complexos da
e ca
equa¸ao
c˜
a y + b y + c y = g1 (t) + i g2 (t),
¨ ˙
em que a, b e c s˜o constantes reais, ent˜o
a a
a u + b u + c u = g1 (t)
¨ ˙
a v + b v + c v = g2 (t).
¨ ˙
ıcio: Prove (ii).
Exerc´
Seja ϕ(t) = u(t) + i v(t) uma solu¸˜o particular da equa¸˜o
ca ca
a y + b y + c y = eα t (a0 + · · · + an tn ) eiβ t .
¨ ˙ (3.26)
A parte real do segundo membro de (3.26) ´ eα t (a0 +· · ·+an tn ) cos β t
e
e a parte imagin´ria ´ eα t (a0 + · · · + an tn ) sen β t; segue-se de (ii) que
a e
u(t) = [ϕ(t)]
´ uma solu¸ao de
e c˜
a y + b y + c y = eα t (a0 + · · · + an tn ) cos β t
¨ ˙

70. Eq. Dif. Linear de 2a Ordem
¯ Cap. 3 Eq. N˜o Homogˆnea 62
a e
e
v(t) = [ϕ(t)]
´ uma solu¸ao de
e c˜
a y + b y + c y = eα t (a0 + · · · + an tn ) sen β t.
¨ ˙
Exemplo 3.17. Encontre uma solu¸ao particular da equa¸ao
c˜ c˜
y − 3 y + 2 y = 20 sen 2 t.
¨ ˙
Solucao: Vamos determinar yp (t) como a parte imagin´ria de uma
¸˜ a
solu¸ao com valores complexos ϕ(t) da equa¸ao y − 3 y + 2 y = 20 e2 i t .
c˜ c˜ ¨ ˙
Como e2it n˜o ´ solu¸ao da homogˆnea associada, devemos tentar
a e c˜ e
solu¸ao da forma ϕ(t) = Ae2 i t . Isso implica que
c˜
ϕ(t) = 2 i Ae2 i t
˙ e ϕ(t) = −4 A e2 i t .
¨
Substituindo na equa¸ao diferencial, obtemos (−2 − 6 i) A = 20 ou
c˜
A = −1 + 3 i. Logo,
ϕ(t) = (−1 + 3 i) e2 i t = (−1 + 3 i) (cos 2 t + i sen 2 t).
Logo,
yp (t) = [ϕ(t)] = 3 cos 2 t − sen 2 t.
4o caso: Finalmente seja g(t) uma combina¸ao linear de fun¸˜es dos
¯ c˜ co
tipos descritos nos casos 1, 2 e 3.
Este caso pode ser resolvido usando o chamado Princ´ıpio da
Superposicao de Solucoes, que diz: se ϕ1 ´ solu¸ao da equa¸˜o
¸˜ ¸˜ e c˜ ca
a y + b y + c y = g1 (t)
¨ ˙
e ϕ2 ´ solu¸ao da equa¸˜o
e c˜ ca
a y + b y + c y = g2 (t)
¨ ˙

71. Eq. Dif. Linear de 2a Ordem
¯ Cap. 3 Eq. N˜o Homogˆnea 63
a e
e α1 , α2 s˜o constantes, ent˜o a fun¸ao ϕ(t) = α1 ϕ1 (t) + α2 ϕ2 (t) ´
a a c˜ e
solu¸ao da equa¸˜o
c˜ ca
a y + b y + c y = α1 g1 (t) + α2 g2 (t).
¨ ˙
ıcio: Prove esta afirma¸ao.
Exerc´ c˜
Exemplo 3.18. Determine uma solu¸˜o particular da equa¸˜o:
ca ca
y − 3 y + 2 y = (4 − 6 t) e−t + 20 sen 2 t.
¨ ˙
Solucao: Para encontrar uma solu¸ao particular desta equa¸ao de-
¸˜ c˜ c˜
vemos procurar solu¸˜es particulares yp1 (t) e yp2 (t) das equa¸˜es
co co
y − 3 y + 2 y = (1 + t) e3 t
¨ ˙ e y − 3 y + 2 y = 20 sen 2 t,
¨ ˙
respectivamente, e ent˜o somarmos essas duas solu¸˜es. Temos, do
a co
3t
Exemplo 3.14 que yp1 (t) = (−1/4 + t/2) e e do Exemplo 3.17 que
yp2 (t) = 3 cos 2 t − sen 2 t. Logo,
yp (t) = yp1 (t) + yp2 (t) = −(1 + 2 t) e−t + 3 cos 2 t − sen 2 t .
Exerc´ ıcios 3.4. 1) Determine uma solu¸˜o particular de cada uma
ca
das seguintes equa¸˜es:
co
a) y + 4 y = sen t.
¨ ˙ b) y + 4 y = cos 2 t.
¨
c) y − y = t2 et .
¨ d) y + 2 y + y = e−t .
¨ ˙
e) y − 2 y + 5 y = 2 cos2 t.
¨ ˙ f) y + 4 y = t sen 2 t.
¨
g) y + y = cos t cos 2 t.
¨ h) y − 3 y + 2 y = et + e2 t .
¨ ˙
i) y + y − 6 y = sen t + te2 t .
¨ ˙ j) y + 2 y = 1 + t2 + e−2 t .
¨ ˙
2) a) Seja L(y) = y − 2 λ1 y + λ2 y. Mostre que L[eλ1 t v(t)] = eλ1 t v (t).
¨ ˙ 1 ¨
b) Determine a solu¸ao geral da equa¸ao y − 6 y + 9 y = t3/2 e3 t .
c˜ c˜ ¨ ˙

72. Eq. Dif. Linear de 2a Ordem
¯ Cap. 3 Eq. N˜o Homogˆnea 64
a e
3.4.2 ´ ¸˜ ˆ
Metodo de Variacao dos Parametros (ou
¸˜
Variacao das Constantes)
Este ´ o m´todo mais geral para se encontrar solu¸˜o particular de
e e ca
equa¸ao diferencial n˜o homogˆnea, pois aplica-se tamb´m a equa¸oes
c˜ a e e ` c˜
com coeficientes vari´veis. A desvantagem deste m´todo ´ que ele con-
a e e
duz ao c´lculo de integrais geralmente complicadas. O m´todo consiste
a e
em determinar uma solu¸ao particular da equa¸˜o n˜o homogˆnea
c˜ ca a e
y + a(t) y + b(t) y = g(t)
¨ ˙ [L.N.H.]
uma vez conhecidas duas solu¸˜es linearmente independentes da equa¸˜o
co ca
homogˆnea associada
e
y + a(t) y + b (t)y = 0.
¨ ˙ [L.H.]
Sejam y1 (t) e y2 (t) duas solu¸oes linearmente independentes da [L.H.].
c˜
Vamos procurar uma solu¸˜o particular yp (t) de [L.N.H.] da forma
ca
yp (t) = u1 (t) y1 (t) + u2 (t) y2 (t). (3.27)
¸˜ `
Observacao 3.14. A primeira vista, isto parece n˜o ter sentido,
a
pois estamos substituindo o problema de encontrar uma fun¸ao desco-
c˜
nhecida yp (t) pelo problema de encontrar duas fun¸oes desconhecidas
c˜
u1 (t) e u2 (t), que aparentemente ´ mais dif´
e ıcil. Entretanto, se traba-
lharmos corretamente encontraremos u1 (t) e u2 (t) como as solu¸oes de
c˜
duas equa¸oes de 1a ordem muito simples.
c˜ ¯
Nosso objetivo, agora, ´ impor condi¸oes sobre u1 e u2 de modo
e c˜
que a express˜o yp + a yp + b yp se torne t˜o simples quanto poss´
a ¨ ˙ a ıvel.
Derivando (3.27), obtemos
yp = u1 y1 + u2 y2 + u1 y1 + u2 y2 .
˙ ˙ ˙ ˙ ˙
Para simplificar as express˜es de yp e yp , vamos impor sobre u1 e u2 a
o ˙ ¨
condi¸ao:
c˜
u1 y1 + u2 y2 = 0.
˙ ˙

73. Eq. Dif. Linear de 2a Ordem
¯ Cap. 3 Eq. N˜o Homogˆnea 65
a e
Com isto, temos
yp = u1 y1 + u1 y1 + u2 y2 + u2 y2 .
¨ ˙ ˙ ¨ ˙ ˙ ¨
Substituindo yp , yp e yp na equa¸ao [L.N.H.] e agrupando convenien-
˙ ¨ c˜
temente, obtemos
u1 y1 + u2 y2 + u1 [¨1 + a y1 + b y1 ] + u2 [¨2 + a y2 + b y2 ] = g.
˙ ˙ ˙ ˙ y ˙ y ˙
Como y1 e y2 s˜o solu¸˜es da homogˆnea, vem
a co e
u1 y1 + u2 y2 = g.
˙ ˙ ˙ ˙
Ent˜o, yp = u1 y1 + u2 y2 ´ uma solu¸ao da [L.N.H.] se u1 e u2 satisfi-
a e c˜
zerem as duas condi¸oes:
c˜
y1 u1 + y2 u2 = 0
˙ ˙
y1 u1 + y2 u2 = g
˙ ˙ ˙ ˙
que ´ um sistema linear em u1 e u2 cujo determinante da matriz dos
e ˙ ˙
coeficientes ´ W (t) = W [ y1 , y2 ](t). Note W (t) ´ diferente de zero,
e e
pois y1 e y2 s˜o solu¸˜es linearmente independentes da [L.H.]. Logo,
a co
g y2 g y1
u1 = −
˙ e u2 =
˙ .
W W
Finalmente, por integra¸˜o, obtemos u1 e u2 e, conseq¨entemente, yp .
ca u
Observacao 3.15. A solu¸˜o geral de [L.H.] ´
¸˜ ca e
y(t) = c1 y1 (t) + c2 y2 (t).
Fazendo c1 e c2 variar com o tempo, obtemos uma solu¸˜o da [L.N.H.].
ca
Da´ o nome varia¸˜o dos parˆmetros (ou constantes).
ı, ca a
Exemplo 3.19. Determine uma solu¸˜o particular da equa¸˜o
ca ca
t
y − y = 4e .
¨
Solucao: Primeiramente, devemos encontrar duas solu¸oes linear-
¸˜ c˜
mente independentes da homogˆnea associada y − y = 0. A equa¸ao
e ¨ c˜

74. Eq. Dif. Linear de 2a Ordem
¯ Cap. 3 Eq. N˜o Homogˆnea 66
a e
caracter´ ıstica λ2 −1 = 0 possui duas ra´ distintas λ1 = 1 e λ2 = −1.
ızes
t −t
Portanto, y1 (t) = e e y2 (t) = e s˜o solu¸˜es da homogˆnea com
a co e
W [ y1 , y2 ](t) = −2 = 0. Ent˜o yp (t) = u1 (t) y1 (t) + u2 (t) y2 (t), em
a
que
−g(t) y2 (t) −4 et e−t
u1 (t) =
˙ = = 1 =⇒ u1 (t) = 2 t
W −2
e
g(t) y1 (t) 4 et et
u2 (t) =
˙ = = −2 e2 t =⇒ u2 (t) = −e2 t .
W −2
Logo, uma solu¸˜o particular de y − y = 2et ´:
ca ¨ e
yp (t) = 2 t et − et .
Exerc´ ıcios 3.5. 1) Encontre a solu¸ao geral, usando o m´todo de
c˜ e
varia¸˜o dos parˆmetros para determinar uma particular, de:
ca a
a) y + y = tg t,
¨ no intervalo 0 t π/2.
b) y − 5 y + 6 y = t et .
¨ ˙ c) y + 2 y + y = 3 e−t .
¨ ˙
d) y − 4 y + 3 y = et /(1 + et ).
¨ ˙ e) y + y = cos2 t.
¨
f) t2 y + t y − y = 4.
¨ ˙ g) t2 y − 2 y + 2 y = t4 .
¨ ˙
h) t2 y − 2 t y + 2 y = t−2 .
¨ ˙ i) t¨ − y = 2 t2 et .
y ˙
Sugestao: Nos exerc´
˜ ıcios f, g, h e i determine por tentativa uma
base de solu¸˜es para as homogˆneas associadas.
co e
2) Sabendo-se que as fun¸˜es t−1/2 sen t e t−1/2 cos t s˜o solu¸oes
co a c˜
2 2
linearmente independentes da equa¸˜o t y + t y + (t − 1/4) y = 0,
ca ¨ ˙
t 0, encontre a solu¸˜o geral de t y + t y + (t − 1/4) y = 3 t3/2 sen t.
ca 2
¨ ˙ 2
3) Determine duas solu¸˜es LI de t2 y − 2 y = 0 da forma y(t) = tr .
co ¨
Usando essas duas solu¸oes, determine a solu¸ao geral de t2 y −2 y = t2 .
c˜ c˜ ¨
4) Uma solu¸ao da equa¸˜o y + p(t) y + q(t) y = 0 ´ (1 + t)2 , e
c˜ ca ¨ ˙ e

75. Eq. Dif. Linear de 2a Ordem
¯ Cap. 3 Aplica¸˜es 67
co
o wronskiano de duas solu¸oes quaisquer, desta equa¸ao, ´ constante.
c˜ c˜ e
Determine a solu¸˜o geral de: y + p(t) y + q(t) y = 1 + t.
ca ¨ ˙
3.5 ¸˜
Algumas Aplicacoes
3.5.1 ¸˜ ˆ
Vibracoes Mecanicas
(a) Vibracoes Amortecidas Forcadas
¸˜ ¸
Consideremos o sistema massa-mola enunciado no Cap´ ıtulo 1, Se¸ao
c˜
1.1.3, e suponhamos que esteja imerso em um meio, tal como oleo, que
´
ofere¸a uma for¸a de resistˆncia ao movimento (atrito) que em geral ´
c c e e
proporcional ` velocidade. Este problema, estudado no Exemplo 3.7,
a
s˜o as vibra¸˜es livres amortecidas. Analisemos agora o problema em
a co
que a massa est´ sujeita a uma for¸a externa F (t) = F0 cos ωt. Ent˜o
a c a
a equa¸ao diferencial que nos d´ o movimento da massa ´
c˜ a e
m y + c y + k y = F0 cos ω t.
¨ ˙
Usando o m´todo dos coeficientes a determinar, encontramos uma
e
solu¸ao particular
c˜
F0
yp (t) = [(k − m ω 2 ) cos ω t + c ω sen ω t]
(k − m ω 2 )2 + c2 ω 2
F0
= 2 )2 + c2 ω 2
[(k − m ω 2 )2 + c2 ω 2 ]1/2 cos(ω t − α)
(k − m ω
F0 cos(ω t − α)
= ,
[(k − m ω 2 )2 + c2 ω 2 ]1/2
em que α = arctg(c ω/(k − m ω 2 )). Portanto, toda solu¸ao y(t) da
c˜
equa¸ao acima ´ da forma
c˜ e
F0 cos(ω t − α)
y(t) = ϕ(t) + ,
[(k − m ω 2 )2 + c2 ω 2 ]1/2

76. Eq. Dif. Linear de 2a Ordem
¯ Cap. 3 Aplica¸˜es 68
co
onde ϕ(t) ´ uma solu¸ao da equa¸ao homogˆnea associada. Conforme
e c˜ c˜ e
vimos no Exemplo 3.7 temos que ϕ(t) → 0 quando t → ∞. Portanto,
para t grande, y(t) = yp (t) descreve muito precisamente a posi¸ao da
c˜
massa m, independentemente de sua posi¸ao e velocidade iniciais. Por
c˜
esta raz˜o, yp (t) ´ chamada a parte estacion´ria da solu¸˜o e ϕ(t)
a e a ca
´ chamada a parte transit´ria da solu¸ao.
e o c˜
(b) Vibracoes Forcadas nao Amortecidas
¸˜ ¸ ˜
Consideremos o problema acima com c = 0, isto ´, sem amorteci-
e
mento. Ent˜o a equa¸˜o diferencial que nos d´ o movimento da massa
a ca a
´
e
m y + k y = F0 cos ω t
¨
ou
2 F0
y + ω0 y =
¨ cos ω t,
m
2 k
em que ω0 = .
m
O caso ω = ω0 n˜o tem interesse. Toda solu¸ao ´ da forma
a c˜ e
F0
y(t) = c1 cos ω0 t + c2 sen ω0 t + 2
cos ω t.
m (ω0 − ω 2 )
Portanto, ´ soma de duas fun¸oes peri´dicas de per´
e c˜ o ıodos diferentes. O
caso interessante ´ aquele em que ω = ω0 , isto ´, quando a freq¨ˆncia
e e ue
ω da for¸a externa ´ igual a freq¨ˆncia natural do sistema. Este caso
c e ue
´ chamado de ressonˆncia e a equa¸˜o diferencial do movimento da
e a ca
massa ´e
2 F0
y + ω0 y =
¨ cos ω0 t. (3.28)
m
Encontraremos uma solu¸ao particular yp (t) de (3.28) como a parte
c˜
real de uma solu¸ao com valores complexos da equa¸ao
c˜ c˜
2 F0 i ω0 t
y + ω0 y =
¨ e . (3.29)
m

77. Eq. Dif. Linear de 2a Ordem
¯ Cap. 3 Aplica¸˜es 69
co
Como ei ω0 t ´ solu¸˜o da equa¸ao homogˆnea y + ω0 y = 0, a equa¸ao
e ca c˜ e ¨ 2
c˜
i ω0 t
(3.29) tem uma solu¸˜o da forma ϕ(t) = A t e
ca , para alguma cons-
tante A. Ent˜oa
ϕ(t) = A ei ω0 t + i ω0 A t eiω0 t
˙ e ϕ(t) = 2 i ω0 A ei ω0 t − ω0 A t ei ω0 t .
¨ 2
Logo,
F0 i ω0 t
e = ϕ + ω0 ϕ = 2 i ω0 A ei ω0 t .
¨ 2
m
Isto implica que A = −i F0 /(2 m ω0 ) e, portanto,
i F0 t i ω0 t i F0 t
ϕ(t) = − e =− (cos ω0 t + i sen ω0 t)
2 m ω0 2 m ω0
i F0 t i F0 t
= sen ω0 t − cos ω0 t.
2 m ω0 2 m ω0
F0 t
Logo, yp (t) = [ϕ(t)] = sen ω0 t ´ uma solu¸ao particular de
e c˜
2 m ω0
(3.28). Conseq¨entemente, toda solu¸˜o y(t) de (3.28) ´ da forma:
u ca e
F0 t
y(t) = c1 cos ω0 t + c2 sen ω0 t + sen ω0 t.
2 m ω0
T
yp
t
E
Notamos que a soma das duas primeiras parcelas ´ uma fun¸ao
e c˜
peri´dica de t e a terceira parcela representa uma oscila¸˜o de am-
o ca
plitude crescente. Portanto, se a for¸a externa F0 cos ωt, est´ em
c a
ressonˆncia com a freq¨ˆncia natural do sistema, causar´ sempre os-
a ue a
cila¸oes ilimitadas. Tal fenˆmeno foi respons´vel pela queda da Ponte
c˜ o a
de Tacoma ([4]) e muitas outras cat´strofes mecˆnicas.
a a

78. Eq. Dif. Linear de 2a Ordem
¯ Cap. 3 Aplica¸˜es 70
co
3.5.2 ´
Circuitos Eletricos
Consideremos agora um sistema el´trico, o qual serve para mostrar que
e
sistemas f´ısicos inteiramente diversos podem corresponder ` mesma
a
equa¸ao diferencial, o que ilustra o papel unificador que a Matem´tica
c˜ a
representa junto a v´rios fenˆmenos de natureza f´
a o ısica completamente
diferentes. Vamos obter uma correspondˆncia entre sistemas el´tricos
e e
e mecˆnicos que n˜o ´ simplesmente qualitativa, mas estritamente
a a e
quantitativa porque, dado um sistema mecˆnico, podemos construir
a
um sistema el´trico cuja corrente forne¸a os valores exatos do deslo-
e c
camento no sistema mecˆnico, quando introduzimos fatores da escala
a
adequados. A analogia pode ser empregada para construir um mo-
delo el´trico de um dado sistema mecˆnico. Em muitos casos, isto
e a
constitui uma simplifica¸ao essencial, porque os circuitos el´tricos s˜o
c˜ e a
f´ceis de montar e as correntes e tens˜es s˜o medidas com facilidade,
a o a
enquanto a constru¸˜o de um modelo mecˆnico pode ser complicada
ca a
e cara, e a medida dos deslocamentos, demorada e imprecisa.
Examinemos o circuito RLC representado na figura abaixo, em
que E representa uma fonte de for¸a eletromotriz (gerador ou bateria)
c
que produz uma diferen¸a de potencial que produz uma corrente I
c
que passa atrav´s do circuito quando a chave S ´ fechada. R denota
e e
a resistˆncia ao fluxo da corrente (tal como a produzida por uma
e
lˆmpada), L, um indutor (bobina de fio de cobre).
a
E
I
R

79. E
L
C
e rS
e
Quando a corrente passa atrav´s da bobina, produz-se um campo
e
magn´tico que se op˜e a qualquer mudan¸a na corrente atrav´s desta
e o c e

80. Eq. Dif. Linear de 2a Ordem
¯ Cap. 3 Aplica¸˜es 71
co
bobina. A varia¸˜o de voltagem produzida pela bobina ´ proporcional
ca e
a taxa de varia¸˜o da corrente. A constante de proporcionalidade ´
` ca e
chamada indutˆncia L da bobina.
a
C = capacitor, que consiste geralmente de duas placas de metal
separadas por um material atrav´s do qual pode passar pouca corrente.
e
Um capacitor tem o efeito de reverter o fluxo da corrente quando uma
das placas se torna carregada.
Seja Q(t) a carga do capacitor no instante t. Para deduzir uma
equa¸ao diferencial satisfeita por Q(t) usaremos a 2a lei de Kirchhoff:
c˜ ¯
“Num circuito fechado, a voltagem aplicada ´ igual ` soma das
e a
quedas de voltagem no resto do circuito.”
Como a queda de voltagem atrav´s do resistor R ´ igual a RI,
e e
dI
atrav´s do indutor L ´ igual a L
e e e atrav´s do capacitor C ´ igual a
e e
dt
Q/C, temos que
dI Q
L + R I + = E(t)
dt C
dQ(t)
e, como I(t) = , vem que
dt
d2 Q dQ Q
L 2
+R + = E(t).
dt dt C
Esta equa¸ao e a equa¸ao do sistema massa-mola, apresentado na
c˜ c˜
Subse¸ao 3.5.1, s˜o essencialmente a mesma. Isto mostra que o circuito
c˜ a
RLC ´ o an´logo el´trico ao sistema mecˆnico da aplica¸˜o anterior, e
e a e a ca
podemos estabelecer a seguinte correspondˆncia entre as quantidades
e
el´tricas e mecˆnicas.
e a
indutˆncia L
a ←→ massa m
resistˆncia R
e ←→ constante de amortecimento c
rec´
ıproco da capacitˆncia 1/C
a ←→ constante da mola k
for¸a eletromotriz E(t)
c ←→ for¸a aplicada F (t)
c
carga Q(t) ←→ deslocamento y(t).

81. Eq. Dif. Linear de 2a Ordem
¯ Cap. 3 Aplica¸˜es 72
co
3.5.3 ¸˜
Outras Aplicacoes
1) Um modelo para descoberta de diabetes ([4] - pag. 157).
2) Lei da Gravita¸ao de Newton e o movimento dos Planetas ([11] -
c˜
pag.647).
3) Um modelo de popula¸˜o ([9] - pag. 111).
ca
4) Propaga¸˜o de ondas monocrom´ticas em um meio unidimensional
ca a
([1] - pag. 128).
5) Deflex˜o de vigas ([10] - pag. 108).
a
6) Cabos suspensos ([10] - pag. 112).
Exerc´ ıcios 3.6. 1) Um indutor de 0, 2 henrys, um resistor de 16
ohms e um capacitor de 0,02 farads s˜o ligados em s´rie com uma
a e
for¸a eletromotriz de E volts. No instante t = 0 a carga do capacitor
c
e a corrente no circuito s˜o nulas. Encontre a carga e a corrente em
a
qualquer instante t 0, se: a) E = 300 volts; b) E = 100 sen 3 t volts.
2) Determine a corrente estacion´ria em um circuito RLC, em que:
a
a) R = 20 ohms; L = 10 henrys; C = 0,05 farad; E = 50 sen t volts.
b) R = 40 ohms; L = 10 henrys; C = 0,02 farad; E = 800 cos t volts.
3) Encontrou-se experimentalmente que 9,44 N de peso esticam
uma mola em 15,24 cm. Se o peso ´ puxado para baixo adicionalmente
e
em 7,62 cm e solto, determine a amplitude, per´ıodo e freq¨ˆncia do
ue
movimento, desprezada a resistˆncia do ar. (A massa m de um objeto
e
em termos de seu peso, ω, ´ m = ω/g = ω/9, 8).
e
4) Um sistema massa-mola amortecido com m = 1, k = 2 e c = 2
(em suas respectivas unidades) est´ suspenso em equil´
a ıbrio. Uma for¸a
c
externa F (t) = (π − t) N atua sobre o sistema entre t = 0 e t = π.
Determine a posi¸˜o da massa em qualquer instante t π.
ca

82. Eq. Dif. Linear de 2a Ordem Cap. 3
¯ Eq. de Ordem Superior 73
3.6 ¸˜
Equacoes de Ordem Superior
Discutiremos, aqui, rapidamente as equa¸oes diferenciais lineares
c˜
de ordem superior, pois toda teoria desenvolvida para a equa¸˜o linear
ca
a ordem pode ser estendida para a equa¸ao de ordem n.
de 2¯ c˜
y (n) + a1 (t) y (n−1) + · · · + an−1 (t) y + an (t) y = g(t),
˙ [L.N.H.]
em que n ´ qualquer n´mero natural.
e u
O pr´ximo teorema cont´m os principais resultados sobre as equa-
o e
¸oes de ordem n. Sua demonstra¸ao ser´ omitida, pois ´ simples
c˜ c˜ a e
adapta¸ao do que j´ foi visto.
c˜ a
Teorema 3.7. Suponhamos que a1 (t), . . ., an (t) e g(t) sejam fun¸˜es
co
cont´nuas num intervalo I. Ent˜o:
ı a
(i) O conjunto de todas as solu¸˜es da equa¸˜o homogˆnea
co ca e
y (n) + a1 (t) y (n−1) + · · · + an−1 (t) y + an (t)y = 0
˙ [L.H.]
´ um espa¸o vetorial de dimens˜o n.
e c a
(ii) Sejam y1 (t), . . ., yn (t) solu¸˜es de [L.H.]. Estas fun¸˜es s˜o
co co a
linearmente independentes se, e somente, se
 
y1 (t0 ) ··· yn (t0 )
.
. .
.
det  =0
 
. .
(n−1) (n−1)
y1 (t0 ) · · · yn (t0 )
para algum t0 ∈ I. Este determinante ´ chamado Wronskiano de
e
y1 , . . . , y n .
(iii) Se yp (t) ´ uma solu¸˜o particular de [L.N.H.] e y1 , . . . , yn s˜o
e ca a
solu¸˜es linearmente independentes de [L.H.], ent˜o a solu¸˜o geral
co a ca
y(t) de [L.N.H.] ´ da forma
e
n
y(t) = yp (t) + cj yj (t).
j=1

83. Eq. Dif. Linear de 2a Ordem Cap. 3
¯ Eq. de Ordem Superior 74
No caso em que a1 , . . . , an s˜o constantes, temos que y(t) = eλ t ´
a e
solu¸ao de [L.H.] se, e somente, se λ ´ raiz da equa¸˜o caracter´
c˜ e ca ıstica
λn + a1 λn−1 + · · · + an−1 λ + an = 0. (3.30)
Como antes, temos trˆs casos a considerar:
e
a) A equa¸ao caracter´
c˜ ıstica (3.30) possui n ra´
ızes reais distintas
λ1 , . . . , λn . Ent˜o, as fun¸oes
a c˜
eλ1 t , eλ2 t , . . . , eλn t
s˜o solu¸˜es reais linearmente independentes de [L.H].
a co
b) A equa¸ao (3.30) possui n ra´
c˜ ızes distintas λ1 , λ2 , . . . , λn , mas
algumas s˜o complexas. Se α + iβ = 0, β = 0, ´ uma raiz de (3.30),
a e
(α+βi)t
ent˜o e
a ´ uma solu¸ao complexa de [L.H] a qual d´ origem a
e c˜ a
duas solu¸oes reais linearmente independentes:
c˜
u(t) = (e(α+i β) t ) = eα t cos β t
e
v(t) = (e(α+i β) t ) = eα t sen β t.
c) As ra´ λ1 , λ2 , . . . , λn n˜o s˜o todas distintas. Se λ ´ uma raiz
ızes a a e
de (3.30) com multiplicidade k, ent˜o as fun¸˜es eλ t , t eλ t , . . . , tk−1 eλ t
a co
s˜o k solu¸oes linearmentes independentes de [L.H].
a c˜
Daremos agora, alguns fatos que nos ajudar˜o na determina¸ao de
a c˜
ra´ de polinˆmios.
ızes o
i) Dada a equa¸ao
c˜
λn + an−1 λn−1 + · · · + a1 λ + a0 = 0, (3.31)
onde a0 , a1 , . . . , an−1 s˜o inteiros, suas prov´veis ra´ inteiras s˜o os
a a ızes a
divisores de a0 .

84. Eq. Dif. Linear de 2a Ordem Cap. 3
¯ Eq. de Ordem Superior 75
ii) Se λ1 ´ uma raiz de (3.31), ent˜o o algoritmo de Briot-Ruffini
e a
´:
e
1 an−1 an−2 ··· a1 a0
λ1 1 λ1 + an−1 λ1 bn−2 + an−2 ··· λ 1 b 1 + a1 0
bn−1 bn−2 bn−3 b0
e, portanto,
λn +an−1 λn−1 +· · ·+a1 λ+a0 = (λ−λ1 )(λn−1 +bn−2 λn−2 +· · ·+b1 λ+b0 ).
(iii) Raiz n-´sima de um n´mero complexo:
e u
Observamos primeiramente que todo n´mero complexo z pode ser
u
iθ
escrito na forma z = re . De fato, se z = x + iy, na figura abaixo
vemos que x = r cos θ e y = r sen θ. Logo, z = r(cos θ + i sen θ) = rei θ
T z = x + iy
T
r
y = r sen θ
θ
c E
' E
x = r cos θ
A raiz n-´sima de um n´mero complexo z = rei θ ´ dada por
e u e
√ √ θ + 2kπ θ + 2kπ
n
z = n r(cos + i sen ), k = 0, 1, 2, . . . , n − 1.
n n
Exemplo 3.20. Calcule as ra´ quartas de −1.
ızes
Solucao: Temos que −1 = cos π + i sen π = ei π = ei(π+2 k π) , k ∈ Z.
¸˜
Logo,
√4
√
4 π + 2kπ π + 2kπ
−1 = 1(cos + i sen ).
4 4

85. Eq. Dif. Linear de 2a Ordem Cap. 3
¯ Eq. de Ordem Superior 76
√
π π 2
k = 0 =⇒ z1 = cos + i sen = (1 + i),
4 4 2 √
3π 3π − 2
k = 1 =⇒ z2 = cos + i sen = (1 − i),
4 4 2
√
5π 5π − 2
k = 2 =⇒ z3 = cos + i sen = (1 + i),
4 4 √2
7π 7π 2
k = 3 =⇒ z4 = cos + i sen = (1 − i).
4 4 2
Exerc´
ıcios:
1) Calcule as ra´ quartas de −16.
ızes
2) Calcule as ra´ quintas de −1.
ızes
3) Calcule as ra´ sextas de 3.
ızes
Exemplo 3.21. Determine a solu¸˜o geral real da equa¸ao diferencial
ca c˜
y (3) + y − 10 y = 0.
˙
Solucao: A equa¸ao caracter´
¸˜ c˜ ıstica ´ λ3 + λ − 10 = 0 tem por ra´
e ızes:
λ1 = 2, λ2 = −1 + 2 i e λ3 = −1 − 2 i. Portanto, y1 (t) = e2 t , y2 (t) =
e−t cos 2 t e y3 (t) = e−t sen 2 t s˜o solu¸˜es linearmente independentes.
a co
Ent˜o a solu¸ao geral ´
a c˜ e
y(t) = c1 e2 t + e−t (c2 cos 2 t + c3 sen 2 t).
Exemplo 3.22. Idem para y (3) + 3 y + 3 y + y = 0.
¨ ˙
Solucao: A equa¸ao caracter´
¸˜ c˜ ıstica ´ λ3 + 3 λ2 + 3 λ + 1 = 0 ou (λ +
e
3
1) = 0. Logo, λ = −1 ´ raiz com multiplicidade 3 e, portanto, y1 (t) =
e
e−t , y2 (t) = t e−t e y3 (t) = t2 e−t formam um sistema fundamental de
solu¸oes. Ent˜o a solu¸ao geral ´
c˜ a c˜ e
y(t) = e−t (c1 + c2 t + c3 t2 ).
Exemplo 3.23. Idem para y (4) + y = 0.

86. Eq. Dif. Linear de 2a Ordem Cap. 3
¯ Eq. de Ordem Superior 77
Solucao: A equa¸ao caracter´ √ ´ λ4 + 1 = 0 ou λ4 = −1. Pelo
¸˜ c˜ ıstica e √
2 2
Exemplo 3.20, temos que λ1 = (1 + i), λ2 = − (1 − i), λ3 =
√ √ 2 2
2 2
− (1 + i) e λ4 = (1 − i) s˜o as quatro ra´
a ızes da equa¸aoc˜
2 2
4
λ = −1. As ra´ ızes λ4 e λ3 s˜o as conjugadas complexas de λ1 e λ2 ,
a
respectivamente. Assim,
√ √
√ 2 2
λ1 t t 2/2
ϕ1 (t) = e = e (cos t + i sen t)
2 2
e √ √
√ 2 2
λ3 t − 2 t/2
ϕ2 (t) = e = e (cos t + i sen t)
2 2
s˜o duas solu¸oes com valores complexos, o que implica que
a c˜
√ √ √ √
2 t/2 2 2 t/2 2
y1 (t) = e 2
t,
cos y2 (t) = e sen 2
t,
√ √ √ √
y3 (t) = e− 2 t/2 cos 22 t y4 (t) = e− 2 t/2
sen 2
2
t
s˜o quatro solu¸oes reais linearmente independentes. Logo, a solu¸ao
a c˜ c˜
real geral ´
e
√ √
√ 2 2
2 t/2
y(t) = e c1 cos t + c2 sen t +
2 2
√ √
√ 2 2
− 2 t/2
+e c3 cos t + c4 sen t .
2 2
Exerc´ ıcios 3.7. 1) Determine a solu¸ao geral de cada uma das
c˜
seguintes equa¸oes:
c˜
a) y + 3 y − 4 y = 0.
¨ ˙ b) y (4) + 2 y + y = 0.
¨
c) y (3) − 2 y − y + 2 y = 0.
¨ ˙ d) y (4) − 5 y (3) + 6 y + 4 y − 8 y = 0.
¨ ˙
e) y (3) + y − 6 y = 0.
¨ ˙ f) y (3) + y + 3y − 5 y = 0.
¨ ˙
g) y (4) + 8 y + 16 y = 0.
¨ h) y (4) + 2 y (3) + 5 y = 0.
¨

87. Eq. Dif. Linear de 2a Ordem Cap. 3
¯ Eq. de Ordem Superior 78
2) Resolva cada um dos P.V.I.
y (5) − 2 y (4) + y (3) = 0
a)
y(0) = y(0) = y (0) = y (3) (0) = 0, y (4) (0) = −1.
˙ ¨
y (3) + y − 6y = 0
¨ ˙
b)
y(0) = y(0) = 1, y (0) = 2.
˙ ¨
y (3) − y = 0
˙
c)
y(0) = 0, y(0) = 1, y (0) = 2.
˙ ¨
y (6) − y = 0
¨
d)
y(0) = y(0) = y (0) = y (3) (0) = y (4) (0) = y (5) (0) = 0.
˙ ¨
3) Mostre que a equa¸˜o diferencial t3 y (3) − 6 t y + 12 y = 0 possui
ca ˙
trˆs solu¸˜es linearmente independentes da forma y(t) = tr .
e co
4) Sabendo-se que y1 (t) = et cos t ´ uma solu¸˜o de y (4) − 2 y (3) +
e ca
y + 2 y − 2 y = 0, determine sua solu¸ao geral. Sugest˜o: Use esta
¨ ˙ c˜ a
informa¸ao para determinar as ra´ da sua equa¸˜o caracter´
c˜ ızes ca ıstica.
Consideremos, agora, a equa¸˜o n˜o homogˆnea
ca a e
y (n) + a1 (t) y (n−1) + · · · + an−1 (t) y + an (t) y = g(t),
˙ [L.N.H.]
Um fato importante sobre [L.N.H.] ´
e
“Se y1 (t), y2 (t), . . . , yn (t) s˜o n solu¸oes linearmente independentes
a c˜
de [L.H.] e yp (t) ´ uma solu¸ao particular da [L.N.H.], ent˜o toda
e c˜ a
solu¸ao de [L.N.H.] ´ da forma
c˜ e
n
y(t) = cj yj (t) + yp (t),
j=1
em que c1 , c2 , . . . , cn s˜o constantes.”
a

88. Eq. Dif. Linear de 2a Ordem
¯ Cap. 3 Coef. a Determinar 79
Logo, como no caso das equa¸˜es de segunda ordem, para deter-
co
minarmos a solu¸ao geral de [L.N.H.] precisamos saber encontrar uma
c˜
solu¸ao particular de [L.N.H.].
c˜
3.7 ´
Metodo dos Coeficientes a Deter-
minar
Este m´todo para [L.N.H.] de ordem n funciona do mesmo modo
e
que para as de segunda ordem.
Exemplo 3.24. Encontre uma solu¸ao particular da equa¸ao
c˜ c˜
(3) t
y − 3y + 3y − y = e .
¨ ˙
Solucao: A equa¸˜o caracter´
¸˜ ca ıstica λ3 − 3 λ2 + 3 λ − 1 = (λ − 1)3 = 0
tem λ = 1 como raiz tripla. Logo, y1 (t) = et , y2 (t) = t et e y3 (t) =
t2 et formam um sistema fundamental de solu¸˜es para a homogˆnea
co e
3 t
associada. Ent˜o devemos tentar yp (t) = A t e . Portanto,
a
yp (t) = A et (t3 + 3 t2 ), yp (t) = A et (t3 + 6 t2 + 6 t) e
˙ ¨
(3) t 3 2
yp (t) = A e (t + 9 t + 18 t + 6).
Substituindo na equa¸˜o e cancelando o fator et , obtemos que A = 1/6.
ca
Logo,
t3 et
yp (t) = .
6
ıcios 3.8. 1) Determine a solu¸ao geral de:
Exerc´ c˜
a) y (3) − y − y + y = 2 e−t + 3.
¨ ˙ b) y (3) + y + y + y = e−t + 4 t.
¨ ˙
(3) (3)
c) y − y = 2 sen t. d) y + y = tg t.
˙
−2 t
e) y − 4 y = t + cos t + 2 e . f) y + 2 y + y = t2 sen t.
(3)
˙ (4)
¨

89. Eq. Dif. Linear de 2a Ordem
¯ Cap. 3 Varia¸ao dos Parˆmetros 80
c˜ a
2) Resolva cada um dos P.V.I.
 (3)  (4)
 y + 4y = t ˙  y + 2y + y = 3t + 4
¨
a) y(0) = y(0) = 0
˙ b) y(0) = y(0) = 0
˙
y (0) = 1.
¨ y (0) = y (3) (0) = 1.
¨
 
 (4)  (3)
 y − y = 3 t + cos t  y + 3 y + 2 y = t + et
¨ ˙
c) y(0) = y(0) = 1
˙ d) y(0) = 1
(3)
y (0) = y (0) = 0.
¨ y(0) = −1/4 y (0) = −3/2.
˙ ¨
 
3.8 ´ ¸˜ ˆ
Metodo de Variacao dos Parametros
Sejam y1 (t), . . . , yn (t) n solu¸oes linearmente independentes de
c˜
[L.H.]. Procuraremos fun¸˜es u1 (t), . . . , un (t) de modo que
co
yp (t) = u1 (t) y1 (t) + · · · + un (t) yn (t)
seja solu¸˜o de [L.N.H.]. Como no caso n = 2, isto ocorrer´ se, e
ca a
somente, se as fun¸oes u1 (t), . . . , un (t) satisfizerem ao sistema
c˜

 y1 u1 + · · · + yn un = 0
 ˙ ˙
 y1 u1 + · · · + yn un = 0
 ˙ ˙
 ˙ ˙
.

.
.
 (n−2) (n−2)
 (n−1) u1 + · · · + yn
 y
 1 ˙ un = 0
˙

(n−1)
y1 u1 + · · · + yn
˙ un = g(t).
˙

Resolvendo o sistema obtemos u1 , . . . , un e, finalmente, por integra¸ao
˙ ˙ c˜
obteremos as fun¸˜es u1 , . . . , un .
co
Observacao 3.16. O sistema acima possui solu¸ao unica pois, o
¸˜ c˜ ´
determinante dos coeficientes W [y1 , . . . , yn ](t) = 0 visto que y1 , . . . , yn
s˜o solu¸˜es linearmente independentes de [L.H.].
a co
Exemplo 3.25. Determine uma solu¸˜o da equa¸ao y (3) + y = sec t.
ca c˜ ˙

90. Eq. Dif. Linear de 2a Ordem
¯ Cap. 3 Varia¸ao dos Parˆmetros 81
c˜ a
Solucao: Primeiramente devemos encontrar uma base de solu¸oes da
¸˜ c˜
(3) 3
homogˆnea associada y + y = 0. A equa¸˜o caracter´
e ˙ ca ıtica λ + λ = 0
tem por ra´ ızes: λ1 = 0, λ2 = i e λ3 = −i. Portanto, y1 (t) = 1,
y2 (t) = cos t e y3 (t) = sen t constitui tal base. Ent˜o, procuramos u1 ,
a
u2 e u3 tais que
yp (t) = u1 (t) + u2 (t) cos t + u3 (t) sen t
seja solu¸ao da equa¸ao n˜o homogˆnea. Resolvendo o sistema
c˜ c˜ a e

 u1 + u2 cos t + u3 sen t = 0
˙ ˙ ˙
−u2 sen t + u3 cos t = 0
˙ ˙
−u2 cos t − u3 sen t = sec t,
˙ ˙

obtemos
u1 = sec t =⇒ u1 (t) = ln | sec t + tg t|,
˙
u2 = −1 =⇒ u2 (t) = −t,
˙
sen t
u3 = −
˙ =⇒ u3 (t) = ln | cos t|.
cos t
Portanto,
yp (t) = ln | sec t + tg t| − t cos t + (sen t) ln | cos t|.
Exerc´ıcios 3.9. 1) Encontre, usando o m´todo de varia¸˜o dos
e ca
parˆmetros, uma solu¸ao particular de cada equa¸ao:
a c˜ c˜
a) y (4) − y = 4 t.
¨ b) y (3) − 3¨ + 3 y − y = et .
y ˙
c) y (3) − 4 y = t + cos t + 2 e−t .
˙ d) y (3) + y + y + y = t + e−t .
¨ ˙
e) y + 2 y + y = t2 sen t.
(4)
¨ f) y (3) − 6 y + 11 y − 6 y = e4 t .
¨ ˙
2) Sabendo-se que t, t2 e 1/t s˜o solu¸˜es da equa¸ao homogˆnea
a co c˜ e
associada a
t3 y (3) + t2 y − 2 t y + 2 y = 2 t4 ,
¨ ˙ t 0,
determine uma solu¸˜o particular da equa¸˜o n˜o homogˆnea.
ca ca a e

91. Cap´
ıtulo 4
Transformada de Laplace
4.1 ´
Integrais Improprias
Seja f (t) uma fun¸ao definida para todo t ≥ a tal que exista a
c˜
b
integral f (t) dt qualquer que seja b a. A integral impr´pria
o
a
de f ´ definida por
e
∞ b
f (t) dt = lim f (t) dt, (4.1)
a b→∞ a
caso o limite exista e seja finito. Neste caso, dizemos que f ´ in-
e
tegr´vel no sentido impr´prio em [a, ∞) ou que a integral impr´pria
a o o
∞
f (t) dt ´ convergente. Caso contr´rio, dizemos que a integral
e a
a
impr´pria ´ divergente.
o e
∞
Por exemplo, a integral impr´pria
o e−t dt ´ convergente, pois
e
0
b
b
lim e−t dt = lim − e−t 0
= lim (1 − e−b ) = 1.
b→∞ 0 b→∞ b→∞
82

92. Transformada de Laplace Cap. 4 Integrais Impr´prias
o 83
∞
dt
A integral impr´pria
o diverge, pois
1 t
b
dt b
lim = lim ln t 1
= ∞.
b→∞ 1 t b→∞
Exerc´ıcios 4.1. 1) Verifique se cada uma das integrais dadas abaixo
converge ou diverge:
∞ ∞ ∞ ∞
dt −t2 ln t dt
a) . b) te dt. c) dt. d) .
2 (t − 1)3/2 0 1 t e t (ln t)2
∞
dx
2) Mostre que a integral ´ convergente se p 1 e ´ diver-
e e
1 xp
gente se p ≤ 1.
Integrais impr´prias em que o integrando depende ainda de uma
o
outra vari´vel s˜o de grande importˆncia em matem´tica e em outras
a a a a
aplica¸oes. O interesse central deste cap´
c˜ ıtulo ´ estudar integrais da
e
forma ∞
e−s t f (t) dt. (4.2)
0
A integral (4.2) define uma fun¸˜o F (s), da vari´vel s. O dom´
ca a ınio
desta fun¸˜o ´ constituido por todos os valores de s tais que esta
ca e
integral seja convergente.
Consideremos, por exemplo
∞
F (s) = e−s t dt. (4.3)
0
Esta integral ´ divergente se s ≤ 0. Para s 0, temos
e
∞ b
1 e−s b 1
e−s t dt = lim e−s t dt = lim − = .
0 b→∞ 0 b→∞ s s s
Deste modo,
1
F (s) = (s 0).
s

93. Transformada de Laplace Cap. 4 Integrais Impr´prias
o 84
Fa¸a o mesmo para as integrais abaixo e obtenha as igualdades:
c
∞ ∞
−s t 1 1
a) e t dt = 2 (s 0). b) e−s t sen t dt = (s 0).
0 s 0 s2 +1
∞ ∞
2 1
c) e−s t t2 dt = (s 0). d) e−s t senh t dt = (s 1).
0 s3 0 s2 −1
[sugest˜o: senh t = (et − et )/2].
a
As integrais acima sugerem que o dom´ da fun¸˜o F (s) seja um
ınio ca
intervalo da forma (a, ∞). Pode-se mostrar que isto ´ verdadeiro em
e
geral.
4.2 A Transformada de Laplace
Seja f (t) uma fun¸˜o definida para todo t ≥ 0. A fun¸˜o
ca ca
∞
F (s) = e−s t f (t) dt (4.4)
0
´ chamada transformada de Laplace de f (t), e denotada por L[f (t)].
e
Exemplo 4.1. De acordo com o exemplo da se¸ao anterior temos para
c˜
s0 ∞
1
L[1] = e−s t dt = .
0 s
Exemplo 4.2. Para s c, temos
b
e(c−s) t b 1
L[ec t ] = lim e−s t ec t dt = lim = .
b→∞ 0 b→∞ c−s 0 s−c
Exemplo 4.3. Integrando por partes duas vezes temos
b b
−s t w e−s t sen w t − s e−s t cos w t
e cos w t dt = ,
0 s2 + w 2 0

94. Transformada de Laplace Cap. 4 Algumas Propriedades 85
b b
−s t w e−s t cos wt − s e−s t sen w t
e sen w t dt = .
0 s2 + w 2 0
Fazendo b → ∞ em cada uma destas igualdades obtemos, para s 0,
s w
L[cos w t] = 2 2
e L[sen w t] = 2 .
s +w s + w2
Exemplo 4.4. C´lculo de L[tn ] para n inteiro positivo. Integrando
a
por partes, temos (para s 0)
b b
tn e−s t b n
L[tn ] = lim e−s t tn dt = lim − + e−s t tn−1 dt
b→∞ 0 b→∞ s 0 s 0
∞
n n
= e−s t tn−1 dt = L[tn−1 ].
s 0 s
1 1
Assim, se n = 1, temos L[t] = L[1] = 2 .
s s
n n−1 n(n − 1) n−2 n!
Se n ≥ 2, temos L[tn ] = L[t ] = 2
L[t ] = · · · = n+1 .
s s s
4.3 Algumas Propriedades
As propriedades que enunciamos a seguir s˜o de grande utilidade
a
para o c´lculo de transformadas.
a
Propriedade 1 (Linearidade): Se L[f (t)] = F (s), L[g(t)] = G(s)
e a, b s˜o constantes, ent˜o
a a
L[a f (t) + b g(t)] = a F (s) + b G(s) = a L[f (t)] + b L[g(t)].
De fato,
∞
L[a f (t) + b g(t)] = e−s t [a f (t) + b g(t)] dt =
0
∞ ∞
=a e−s t f (t) dt + b e−s t g(t) dt
0 0
= a L[f (t)] + b L[g(t)].

95. Transformada de Laplace Cap. 4 Algumas Propriedades 86
Exemplo 4.5. Calculemos L[senh a t], usando a Propriedade 1.
1 1 1
L[senh a t] = L[ (ea t − e−a t )] =
L[ea t ] − L[e−a t ]
2 2 2
1 1 1 a
= − = 2 , s |a|.
2 s−a s+a s − a2
s
De modo an´logo obtemos L[cosh a t] = 2
a , para s |a|.
s − a2
Propriedade 2: Se L[f (t)] = F (s), para s s0 , ent˜o
a
L[ea t f (t)] = F (s − a), para s s0 + a. (4.5)
De fato,
∞ ∞
L[ea t f (t)] = e−s t ea t f (t) dt = e−(s−a) t f (t) dt = F (s − a).
0 0
Usando esta propriedade e os exemplos precedentes, podemos es-
crever
ω s−a
L[ea t sen ω t] = L[ea t cos ω t] =
(s − a)2 + ω 2 (s − a)2 + ω 2
n!
L[ea t tn ] = .
(s − a)n+1
Propriedade 3: Se L[f (t)] = F (s), ent˜o
a
dn
L[tn f (t)] = (−1)n
F (s). (4.6)
dsn
Fa¸amos a verifica¸˜o para n = 1. Temos
c ca
∞ ∞ ∞
d ∂ −s t
F (s) = e−s t f (t) dt = e f (t) dt = − e−s t t f (t) dt.
ds 0 0 ∂s 0
Portanto,
L[t f (t)] = −F (s). (4.7)
Aplicando repetidas vezes a igualdade (4.7), obtemos (4.6).

96. Transformada de Laplace Cap. 4 Algumas Propriedades 87
Exemplo 4.6. Segue de (4.6) com n = 2 e n = 1 que
d2 1 2
L[t2 e5 t ] = 2 s−5
= e
ds (s − 5)3
d 3 6s
L[t sen 3 t] = − 2+9
= 2 .
ds s (s + 9)2
A pr´xima propriedade faz uso do seguinte conceito:
o
Uma fun¸ao f (t) ´ de ordem exponencial se existirem constantes
c˜ e
M , α 0 tais que para todo t suficientemente grande
|f (t)| ≤ M eαt .
As fun¸oes sen t, cos t, ek t e tn (n ≥ 0) s˜o de ordem exponencial
c˜ a
kt kt
pois | sen t| ≤ 1, | cos t| ≤ 1 e |e | = e para todo t ≥ 0. Para a
fun¸ao tn , notemos que, para t suficientemente grande, |tn | ≤ et , pois
c˜
tn
lim t = 0.
t→∞ e
2
A fun¸ao et n˜o ´ de ordem exponencial, uma vez que para qual-
c˜ a e
2
quer α 0 temos que lim et e−α t = ∞.
t→∞
Propriedade 4: Suponha que f e f sejam integr´veis em [0, b],
a
para todo b 0. Se f for de ordem exponencial, ent˜o existe L[f (t)]
a
e
L[f (t)] = s L[f (t)] − f (0). (4.8)
De fato, integrando por partes, temos
b b
e−s t f (t) dt = e−s b f (b) − f (0) + s e−s t f (t) dt.
0 0
Fazendo b → ∞, a integral do 1o membro tende a L[f (t)], a integral
¯
do 2o membro tende a L[f (t)] e a parcela e−s b f (b) tende a zero, pois
¯
f ´ de ordem exponencial (os valores de s devem ser maiores do que
e
a constante α da defini¸ao de ordem exponencial).
c˜

97. Transformada de Laplace Cap. 4 Algumas Propriedades 88
Observacao 4.1. Esta propriedade aplica-se a derivadas de ordem
¸˜
superior. Por exemplo, para a derivada segunda, a igualdade (4.8)
implica
L[f (t)] = s L[f (t)] − f (0)
= s {s L[f (t)] − f (0)} − f (0)
= s2 L[f (t)] − s f (0) − f (0).
Logo,
L[f (t)] = s2 L[f (t)] − s f (0) − f (0). (4.9)
Observacao 4.2. As igualdades (4.8) e (4.9) s˜o de grande im-
¸˜ a
portˆncia, especialmente na resolu¸ao de equa¸oes diferenciais, como
a c˜ c˜
veremos adiante. Estas igualdades tamb´m podem ser utilizadas para
e
obter transformadas de Laplace de fun¸oes. Calculemos, por exem-
c˜
plo, L[ek t ] utilizando (4.8). Notemos que a fun¸˜o f (t) = ek t satisfaz
ca
kt
f (t) = k e e f (0) = 1. Substituindo estes dados em (4.8), obteremos
que L[kek t ] = s L[ek t ] − 1, donde (s − k) L[ek t ] = 1. Logo,
1
L[ek t ] = .
s−k
Exerc´ ıcios 4.2. 1) Calcule a transformada de Laplace das seguintes
fun¸oes:
c˜
a) t2 − 3 t + 2. b) 4 cos 3 t − 5 sen 2 t. c) 2 t e3 t .
1 se 0 t π
d) t2 cos 5 t. e) t e2 t sen 3 t. f) f (t) =
0 se t π.
2) Use a igualdade (4.9) para mostrar que
s ω
L[cos ω t] = L[sen ω t] = .
s2 + ω2 s2 + ω2

98. Transformada de Laplace Cap. 4 Transformada Inversa 89
4.4 ¸˜
Transformada Inversa - Fracoes
Parciais
Dada uma fun¸˜o F (s), definida em um intervalo (a, ∞), um pro-
ca
blema que se coloca ´ o de achar uma fun¸ao f (t) tal que L[f (t)] =
e c˜
F (s). Uma tal f ´ chamada Transformada Inversa de F e ser´
e a
−1
indicada por L [F (s)].
Os exemplos da Se¸ao 4.2 fornecem
c˜
1 1 1 tn
L−1 [ ] = 1 L−1 [ ] = ec t L−1 [ n+1
]=
s s−c s n!
s ω
L−1 [ ] = cos ω t L−1 [ ] = sen ω t.
s2 + ω2 s2 + ω2
Usando esta tabela de transformada inversa e as Propriedades 1,
2 e 3, podemos calcular transformadas inversas de um grande n´mero
u
de fun¸oes.
c˜
1
Exemplo 4.7. Calcule L−1 [ ].
s2 − 4s + 5
Solucao: Notando que s2 − 4s + 5 = (s − 2)2 + 1, e usando a Pro-
¸˜
priedade 2, podemos escrever
1 1
2 − 4s + 5
= 2+1
= L[e2 t sen t].
s (s − 2)
Logo,
1
L−1 [ ] = e2 t sen t.
s2 − 4s + 5
1
Exemplo 4.8. Calcule L−1 [ ].
(s − 5)3

99. Transformada de Laplace Cap. 4 Transformada Inversa 90
d2 1 2
Solucao: Notemos que
¸˜ ( )= , donde
ds2 s − 5 (s − 5)3
1 1 d2 1 1 d2 1 1
3
= (
2 s−5
)= 2
L[e5 t ] = L[t2 e5 t ] = L[ t2 e5 t ].
(s − 5) 2 ds 2 ds 2 2
Logo,
1 1
L−1 [
] = t2 e5 t .
(s − 5)3 2
s+2
Exemplo 4.9. Calcule L−1 [ 2 ].
s + 2 s + 10
Solucao: Podemos escrever s2 + 2 s + 10 = (s + 1)2 + 9, donde
¸˜
s+2 s+1+1 s+1 1 3
= = + .
s2 + 2 s + 10 (s + 1) 2+9 (s + 1) 2 + 32 3 (s + 1)2 + 32
Agora, notemos que
s+1 3
L−1 [ 2 + 32
] = e−t cos 3 t e L−1 [ 2 + 32
] = e−t sen 3 t.
(s + 1) (s + 1)
Portanto,
s+2 1
L−1 [ ] = e−t cos 3 t + e−t sen 3 t.
s2 + 2s + 10 3
Observe que este procedimento aplica-se a express˜es do tipo
o
As + B
(4.10)
s2
+ ps + q
em que o denominador n˜o possui ra´ reais.
a ızes
Isto sugere que usemos o m´todo das fra¸oes parciais para calcu-
e c˜
lar L−1 [P (s)/Q(s)], em que P e Q s˜o polinˆmios e o grau de P ´
a o e
menor que o grau de Q. Este m´todo transforma um tal quociente em
e
uma soma de fra¸˜es da forma (4.10) e fra¸˜es da forma C/(s − a).
co co
Acreditamos que o leitor esteja suficientemente familiarizado com a
decomposi¸ao em fra¸˜es parciais, e vamos apenas exemplificar sua
c˜ co
utiliza¸ao no c´lculo de L−1 .
c˜ a

100. Transformada de Laplace Cap. 4 Transformada Inversa 91
3 s2 − 7 s + 12
Exemplo 4.10. Calcule L−1 [ ].
(s − 2) (s − 3) (s + 2)
3s2 − 7 s + 12 A B c
Solucao: Escrevemos
¸˜ = + + .
(s − 2) (s − 3) (s + 2) s−2 s−3 s+2
Eliminando denominadores, obtemos
A (s − 3) (s + 2) + B (s − 2) (s + 2) + C (s − 2) (s − 3) ≡ 3s2 − 7 s + 12.
Substituindo s = 2, obtemos −4A = 10 o que implica que A = −5/2.
Analogamente, obtemos B = 18/5 e C = 19/10. Temos ent˜oa
3 s2 − 7 s + 12 5 1 18 1 19 1
=− + + .
(s − 2) (s − 3) (s + 2) 2 s−2 5 s − 3 10 s + 2
Portanto,
3 s2 − 7 s + 12 5 18 3 t 19 −2 t
L−1 [ ] = − e2 t + e + e .
(s − 2) (s − 3) (s + 2) 2 5 10
2 s2 + 9 s + 7
Exemplo 4.11. Calcule L−1 [ ].
(s − 4) (s2 + 9)
2 s2 + 9 s + 7 A Bs+C
Solucao: Escrevemos
¸˜ = + 2 . Elimi-
(s − 4) (s2 + 9) s−4 s +9
nando denominadores, obtemos
A (s2 + 9) + (B s + C) (s − 4) ≡ 2 s2 + 9 s + 7
ou (A + B) s2 + (C − 4 B) s + (9 A − 4C) ≡ 2 s2 + 9 s + 7. Igualando
os termos de mesma potˆncia, obtemos
e

 A+B =2
−4 B + C = 9
9 A − 4 C = 7.


101. Transformada de Laplace Cap. 4 Aplica¸˜o a Eq. Diferenciais 92
ca
A solu¸˜o deste sistema ´: A = 3, B = −1 e C = 5. Portanto
ca e
2 s2 + 9 s + 7 1 s−5
L−1 [ 2 + 9)
] = 3 L−1 [ ] − L−1 [ 2 ]
(s − 4)(s s−4 s +9
1 s 5 3
= 3 L−1 [ ] − L−1 [ 2 ] + L−1 [ 2 ]
s−4 s −9 3 s +9
5
= 3 e4 t − cos 3 t + sen 3 t.
3
ıcios 4.3. Calcular a transformada inversa das seguintes fun¸oes:
Exerc´ c˜
1 s s+5
1) . 2) . 3) .
s2 + 4 s + 13 s2 − 6 s + 10 s2 − 2 s + 10
1 6s s+1
4) . 5) . 6) .
(s − 4)2 (s2 + 9)2 s2 + 2 s
6 s2 + 9 s − 9 2s − 4
7) 2 (s2 + 1)
. 8) . 9) .
(s − 1) s3 − 9 s s3 + 4 s
4.5 ¸˜ ¸˜
Aplicacao a Equacoes Diferenciais
A Transformada de Laplace ´ de grande importˆncia na resolu¸ao
e a c˜
de problemas de valor inicial para equa¸oes diferenciais lineares com
c˜
coeficientes constantes.
Veja o seguinte exemplo:
Exemplo 4.12. Consideremos o P.V.I.
y − y − 6 y = 10 e2 t
¨ ˙
(4.11)
y(0) = 3, y(0) = 2.
˙
Determine sua solu¸˜o, utilizando Transformada de Laplace.
ca
Solucao: Chamando L[y(t)] = Y (s), temos
¸˜
L[y(t)] = s L[y(t)] − y(0) = s Y − 3.
˙
(4.12)
L[¨(t)] = s L[y(t)] − y(0) = s2 Y − 3 s − 2.
y ˙ ˙

102. Transformada de Laplace Cap. 4 Aplica¸˜o a Eq. Diferenciais 93
ca
Aplicando a transformada a ambos os membros de (4.11) e substi-
tuindo as igualdades de (4.12), obtemos
10
(s2 − s − 6) Y − 3 s + 1 = ,
s−2
ou seja,
3 s2 − 7 s + 12
Y (s) = .
(s − 2) (s2 − s − 6)
A solu¸˜o y(t) do P.V.I. ´ a transformada inversa de Y (s), que j´ foi
ca e a
calculada no Exemplo 4.10, vale
5 18 3 t 19 −2 t
y(t) = − e2 t + e + e .
2 5 10
A transformada de Laplace tamb´m pode ser usada para obter a
e
solu¸ao geral de uma equa¸ao diferencial. Para determinar a solu¸ao
c˜ c˜ c˜
geral da equa¸˜o
ca
y + a y + b y = f (t),
¨ ˙
basta considerar o P.V.I.
y + a y + b y = f (t)
¨ ˙
y(0) = c1 , y(0) = c2 ,
˙
em que c1 e c2 designam constantes arbitr´rias.
a
Exemplo 4.13. Obter a solu¸˜o geral de y − 3 y + 2 y = 10 sen t.
ca ¨ ˙
Solucao: Formamos o P.V.I.
¸˜
y − 3 y + 2 y = 10 sen t
¨ ˙
y(0) = c1 , y(0) = c2 .
˙
Fazendo L[y(t)] = Y (s), podemos escrever L[y(t)] = s Y −c1 e L[¨(t)] =
˙ y
2
s Y − c1 s − c2 . Aplicando a transformada a ambos os membros da
equa¸ao obtemos
c˜
10
(s2 − 3 s + 2) Y − c1 s − c2 + 3 c1 = .
s2+1

103. Transformada de Laplace Cap. 4 Outras Propriedades 94
Portanto,
c1 s + c2 − 3 c1 10
Y = 2 − 3s + 2
+ 2
s (s + 1)(s2 − 3 s + 2)
c2 − c1 2 c1 − c2 5 2 3s + 1
= + − + + 2 .
s−2 s−1 s−1 s−2 s +1
Logo,
y(t) = (c2 − c1 ) e2 t + (2 c1 − c2 ) et − 5 et + 2 e2 t + 3 cos t + sen t,
que pode ser escrita sob a forma
y(t) = A e2 t + B et + 3 cos t + sen t.
ıcios 4.4. 1) Resolva os seguintes problemas de valor inicial:
Exerc´
y+y =0
¨ y − 6 y + 9 y = 4 et
¨ ˙
a) b)
y(0) = 3, y(0) = 1.
˙ y(0) = 2, y(0) = 4.
˙
y + 9 y = cos 3 t
¨ y − 3 y + 2 y = 3 e−t + 5
¨ ˙
c) d)
y(0) = 2, y(0) = −1.
˙ y(0) = 0, y(0) = 0.
˙
2) Ache a solu¸ao geral das seguintes equa¸oes:
c˜ c˜
a) y − 2 y + y = cos t.
¨ ˙ b) y + 2 y + 5 y = 6 e−t sen t.
¨ ˙
4.6 Outras Propriedades
A fun¸˜o degrau unit´rio ou fun¸˜o de Heaviside, ´ definida
ca a ca e
por
0 se t c,
µc (t) =
1 se t ≥ c.

104. Transformada de Laplace Cap. 4 Outras Propriedades 95
Seu gr´fico ´ dado pela figura ao
a e y T
lado. A transformada de µc (t) ´
e
1
L[µc (t)] =
b
e−c s E
lim e−s t dt = . c t
b→∞ c s
A fun¸˜o µc (t) ´ util para representar fun¸oes descont´
ca e´ c˜ ınuas e calcular
suas transformadas.
Exemplo 4.14. Calcule L[g(t)], sendo
y
 T
 0, se t c,
g(t) = A, se c ≤ t d, A
0, se t ≥ d.

E
c d t
Podemos escrever g(t) = A[µc (t) − µd (t)]. Logo,
A −c s
L[g(t)] = A{L[µc (t)] − L[µd (t)]} = e − e−d s .
s
Dada uma fun¸ao f (t), definida para todo t ∈ R, e uma constante
c˜
c 0, consideremos a fun¸ao µc (t) f (t − c). Desde que
c˜
0 se t c,
µc (t) f (t − c) =
f (t − c) se t ≥ c,
o gr´fico de µc (t) f (t − c) ´ obtido transladando-se de c unidades para
a e
a direita o gr´fico de f (t) (veja as figuras abaixo).
a

105. Transformada de Laplace Cap. 4 Outras Propriedades 96
y T y T
y = f (t) y = µc (t) f (t − c)
E E
t c t
Propriedade 5: L[µc (t) f (t − c)] = e−c s L[f (t)].
De fato,
∞ ∞
−s t
L[uc (t) f (t − c)] = e f (t − c) dt = e−s (τ +c) f (τ ) dτ
c ∞ 0
−s c −s τ
=e e f (τ ) dτ = e−s c L[f (t)].
0
0, se t 2,
Exemplo 4.15. Calcule L[f (t)], sendo f (t) = 3
(t − 2) , se t ≥ 2.
Solucao: Como f (t) = µ2 (t) (t − 2)3 , temos que
¸˜
6 e−2 s
L[f (t)] = e−2 s L[t3 ] = .
s4
Usando esta propriedade, podemos resolver equa¸˜es diferenciais
co
que em certo sentido s˜o “mais complicadas” do que as que foram
a
consideradas anteriormemte e que tem grande interesse em aplica¸oes.
c˜
y + 4 y = f (t)
¨
Exemplo 4.16. Resolva o P.V.I. , em que
 y(0) = y(0) = 0
˙
 0 se 0 t π,
f (t) = 4 se π ≤ t 3 π,
0 se t ≥ 3 π.

4 −π s
Solucao: Do Exemplo 4.14, temos que L[f (t)] =
¸˜ e − e−3 π s .
s

106. Transformada de Laplace Cap. 4 Delta de Dirac 97
Aplicando transformada aos dois membros da equa¸˜o, obtemos
ca
4 e−πs 4 e−3 πs
(s2 + 4) Y (s) = − .
s s
e portanto,
1 s 1 s
Y (s) = e−π s − 2 − e−3 π s − 2 .
s s +4 s s +4
Logo,
y(t) = µπ (t) [1 − cos 2 (t − π)] − µ3π (t) [1 − cos 2 (t − 3 π)]
ou seja 
 0 se t π,
y(t) = 1 − cos 2 (t − π) se π ≤ t 3 π,
0 se t ≥ 3 π.

O gr´fico de y(t) ´
a e
y T
2
1
E
π 2π 3π t
4.7 Delta de Dirac
Em diversos ramos das aplica¸oes, h´ a necessidade de se considerar
c˜ a
fun¸oes que sejam nulas exceto em um intervalo “muito pequeno”
c˜
e, neste intervalo, tenham um valor “muito grande”. Por exemplo,

107. Transformada de Laplace Cap. 4 Delta de Dirac 98
durante o intervalo de tempo [t0 , t0 + ε] (ε pequeno) aplica-se a um
objeto uma for¸a muito grande de modo que o impulso causado por
c
esta for¸a seja um certo valor I0 0. A fun¸˜o
c ca
1/ε se t0 ≤ t ≤ t0 + ε,
fε (t) =
0 nos outros pontos
cujo gr´fico ´ dado na figura ao lado
a e y T
tem estas caracter´
ısticas:
1/ε
∞ t0 +ε
1
fε (t) dt = dt = 1,
−∞ t0 ε
e para ε 0 pequeno f tem um
E
t0 t0 + ε t
valor muito grande (1/ε) num intervalo
muito pequeno (de comprimento ε).
Em F´ ısica e Engenharia, costuma-se descrever tais fenˆmenos usan-
o
do-se a “fun¸˜o limite” de fε (t) quando ε → 0, a qual ´ indicada por
ca e
δ(t − t0 ), e chamada delta de Dirac
δ(t − t0 ) = “ lim fε (t)”.
ε→0
´
E claro que δ n˜o ´ uma fun¸ao nos moldes tradicionais. Entretanto,
a e c˜
´ poss´ dar uma justificativa rigorosa para tais procedimentos.
e ıvel
4.7.1 Transformada de Laplace de δ(t − t0 )
Vamos definir
L[δ(t − t0 )] = lim L[fε (t)].
ε→0
1
Como fε (t) = [µt0 (t) − µt0 + ε (t)], temos
ε
1 e−s t0 e−s (t0 +ε) e−s t0 1 − e−εs
L[fε (t)] = ( − )= .
ε s s s ε

108. Transformada de Laplace Cap. 4 Delta de Dirac 99
1 − e−ε s
Quando ε → 0, temos que → s. Assim,
ε
L[δ(t − t0 )] = e−s t0 .
Exemplo 4.17. Consideremos o seguinte sistema massa-mola.
Na figura ao lado, a part´ ıcula tem massa m = 2kg,
a constante de rigidez da mola ´ k = 8N/m. O
e
sistema est´ inicialmente em repouso. No instante
a k
t = π aplica-se ` part´
a ıcula uma for¸a muito grande,
c
de dura¸ao muito curta, que transmite ` part´
c˜ a ıcula
m
um impulso de 4N.s. Descrever o movimento da
part´ıcula.
A posi¸˜o y(t) da part´
ca ıcula no instante t, satisfaz o P.V.I.
2 y + 8 y = 4 δ(t − π)
¨
y(0) = y(0) = 0.
˙
Aplicando a transformada a ambos os membros da equa¸ao obtemos
c˜
2 −πs
(s + 4) Y (s) = 2 e , ou seja,
2
Y (s) = e−πs .
s2 +4
Portanto,
0 se t π,
y(t) = µπ (t) sen 2 (t − π) =
sen 2 t se t ≥ π.
y T
E
3π
π 2 2π t
Gr´fico da solu¸˜o y(t)
a ca

109. Transformada de Laplace Cap. 4 Convolu¸ao 100
c˜
Exerc´ ıcios 4.5. 1) Calcule a transformada de:
 
 0 se t π,  1 se 0 t 1,
a) f (t) = t−π se π t 2 π, b) f (t) = 3 se 1 t 4
0 se t 2 π. 0 se t 4.
 
2) Calcule L−1 [F (s)], sendo:
e−2 s e−s π/2 s
a) F (s) = . b) F (s) = .
s2 s2 + 1
3) Resolva
y + 4 y = µ2 (t) − µ4 (t),
¨ y + y + 7 y = t [µ1 (t) − µ2 (t)]
¨ ˙
a) b)
y(0) = 3, y(0) = −2.
˙ y(0) = 0, y(0) = 0.
˙
4) Suponha que no exemplo anterior, f (t) = 4δ(t) + 6 δ(t − 1) (isto
´, a part´
e ıcula recebe um impulso de 4N.s em t = 0 e um impulso de
6N.s em t = 1). Descrever o movimento. Fa¸a um gr´fico de y(t).
c a
4.8 ¸˜
O Produto de Convolucao
Sejam f (t) e g(t) definidas para t ≥ 0. O Produto de Con-
volu¸˜o de f por g, indicado por f ∗ g, ´ a fun¸˜o definida por
ca e ca
t
(f ∗ g)(t) = f (τ ) g(t − τ ) dτ. (4.13)
0
Por exemplo, se f (t) = cos t e g(t) = t, ent˜o
a
t t t
(f ∗g)(t) = cos τ (t−τ ) dτ = t cos τ dτ − τ cos τ dτ = 1−cos t.
0 0 0
O produto de convolu¸ao possui algumas propriedades semelhantes
c˜

110. Transformada de Laplace Cap. 4 Convolu¸ao 101
c˜
as do produto usual de fun¸oes, tais como:
c˜
a) f ∗ g = g ∗ f, b) (f ∗ g) ∗ h = f ∗ (g ∗ h),
c) f ∗ 0 = 0, d) f ∗ (g + h) = f ∗ g + f ∗ h.
Entretanto, ele ´ diferente do produto usual. Por exemplo, ´ f´cil ver
e e a
t
que (f ∗ 1)(t) = f (τ ) dτ e esta fun¸ao ´ diferente de f (exceto,
c˜ e
0
obviamente, para f = 0).
A pr´xima propriedade nos mostra como a Transformada de Laplace
o
atua em um produto de convolu¸ao.
c˜
Propriedade 6: Se F (s) = L[f (t)] e G(s) = L[g(t)], ent˜o
a
L[(f ∗ g)(t)] = F (s) G(s), (4.14)
ou, em termos de transformada inversa,
L−1 [F (s)G(s)] = (f ∗ g)(t). (4.15)
A igualdade (4.14) implica, em particular (para g(t) ≡ 1), que
t
F (s)
L[ f (τ ) dτ ] = . (4.16)
0 s
A igualdade (4.15) fornece um meio de calcular transformadas in-
versas de certas fun¸˜es. Por exemplo,
co
1 1 1
L−1 [ 2 2
] = L−1 [ 2 ] ∗ L−1 [ 2 ] = sen t ∗ t
(s + 1)s s +1 s
t t t
= sen τ (t − τ ) dτ = t sen τ dτ − τ sen τ dτ
0 0 0
= t − sen t.
A Propriedade 6 aplica-se diretamente ` resolu¸ao de “equa¸oes
a c˜ c˜
integrais do tipo convolu¸˜o” as quais tem a forma
ca
t
y(t) = f (t) + y(τ ) g(t − τ ) dτ, (4.17)
0

111. Transformada de Laplace Cap. 4 Convolu¸ao 102
c˜
onde f e g s˜o fun¸oes conhecidas. O nome equa¸˜o integral deve-se
a c˜ ca
ao fato que a inc´gnita y aparece sob o sinal de integral. Embora n˜o
o a
se trate propriamente de uma equa¸˜o diferencial, julgamos oportuno
ca
apresentar um exemplo.
Consideremos a equa¸˜o
ca
t
y(t) = 3 sen t + 2 y(τ ) sen(t − τ ) dτ. (4.18)
0
Esta equa¸ao pode ser escrita sob a forma
c˜
y(t) = 3 sen t + 2 (y ∗ sen)(t).
Aplicando transformada a ambos os membros de (4.18), obtemos
3 1
Y (s) = + 2 Y (s) 2 .
s2 +1 s +1
Portanto,
3 3 1 1
Y (s) = = ( − ).
s2 −1 2 s−1 s+1
Logo,
3 t
y(t) = (e − e−t ) = 3 senh t.
2
Exerc´ ıcios 4.6. 1) Usando convolu¸ao, calcule a transformada in-
c˜
versa das seguintes fun¸˜es:
co
1 s
a) . b) .
(s − 4)(s − 3) (s2 + 1)(s − 3)
1 1
c) . d) .
s2 − 2s + 1 s2 (s − 5)
2) Resolva as seguintes equa¸˜es integrais:
co
t
a) y(t) = 5 t + y(τ ) sen(t − τ ) dτ .
0

112. Transformada de Laplace Cap. 4 Tabela 103
t
b) y(t) = 2 sen 4 t + 3 y(τ ) sen 4 (t − τ ) dτ .
0
3) Usando Transformada de Laplace, mostre que a solu¸ao geral
c˜
2
da equa¸ao y (t) + ω y(t) = f (t) ´
c˜ ¨ e
t
1
y(t) = c1 cos ωt + c2 sen ωt + f (τ ) sen ω (t − τ ) dτ.
ω 0
4.9 Tabela de Algumas Transformadas
As tabelas abaixo cont´m um resumo das propriedades e transfor-
e
madas de algumas fun¸oes que aparecem com mais freq¨ˆncia.
c˜ ue
Tabela 1 - Algumas Transformadas
f (t) F (s) f (t) F (s)
1
1 1/s ec t
s−c
n! n!
tn tn ec t
sn+1 (s − c)n+1
s c
cosh c t senh c t
s 2 − c2 s2 − c2
s ω
cos ω t sen ω t
s2 + ω2 s2 + ω2
ω 2 − s2 2 ωs
t cos ω t t sen ω t
s2 + ω 2 (s2 + ω 2 )2
δ(t − t0 ) e−s t0

113. Transformada de Laplace Cap. 4 Tabela 104
Tabela 2 - Algumas Propriedades
f (t) F (s) f (t) F (s)
ec t f (t) F (s − c) tn f (t) (−1)n F (n) (s)
µc (t)f (t − c) e−cs F (s) (f ∗ g)(t) F (s)G(s)
f (t) sF (s) − f (0) f (t) s2 F (s) − sf (0) − f (0)

114. Cap´
ıtulo 5
Sistemas de Equa¸oes
c˜
Diferenciais
Consideremos agora sistemas de equa¸˜es diferenciais simultˆneas
co a
em v´rias vari´veis. Um exemplo de tais sistemas ´ dado pelo sistema
a a e
massa-mola mostrado na figura abaixo. Os dois objetos de massas
m1 e m2 movem-se numa superf´ sem atrito, ligados por trˆs molas
ıcie e
cujas constantes de elasticidade s˜o k1 , k2 e k3 , respectivamente, e sob
a
a influˆncia de for¸as externas F1 (t) e F2 (t).
e c
F1 (t) F2 (t)
E E
k1 k2 k3
m1 m2
E E
x1 x2
105

115. Sistemas de Equa¸˜es Diferenciais
co Cap. 5 Teoria Geral 106
O movimento dos objetos ´ descrito pelo par de equa¸oes
e c˜
m1 x1 = −k1 x1 − k2 (x1 − x2 ) + F1 (t),
¨
m2 x2 = −k3 x2 − k2 (x2 − x1 ) + F2 (t).
¨
ou seja
m1 x1 = −(k1 + k2 ) x1 + k2 x2 + F1 (t),
¨
m2 x2 = k2 x1 − (k2 + k3 ) x2 + F2 (t).
¨
Outro exemplo de sistema de equa¸˜es diferenciais ´ encontrado
co e
com freq¨ˆncia no estudo de circuitos el´tricos. Um transformador,
ue e
por exemplo, envolve dois circuitos, sendo que um deles induz uma
corrente no outro por indu¸ao magn´tica. O correspondente sistema
c˜ e
de equa¸oes diferenciais para as correntes I1 e I2 nos circuitos da figura
c˜
abaixo ´:
e

dI1 dI2
 L1 +M + R1 I1 = E1 (t),


 dt dt
 L dI2 + M dI1 + R I = E (t),


 2 2 2 2
dt dt
em que M ´ o coeficiente de indu¸ao m´tua.
e c˜ u
R1 R2

116. E2 (t)
(t)
E1 L1 L2
I1 (t) I2 (t)
' E
Sistemas de equa¸˜es diferenciais tamb´m ocorrem em muitas ou-
co e
tras aplica¸oes como: mistura qu´
c˜ ımica de v´rios ingredientes, cresci-
a
mento de duas ou mais popula¸oes interadas, vibra¸oes de estruturas,
c˜ c˜
etc.

117. Sistemas de Equa¸˜es Diferenciais
co Cap. 5 Teoria Geral 107
5.1 Teoria Geral para Sistemas
Os sistemas de equa¸oes diferenciais de 1a ordem podem, geralmente
c˜ ¯
ser escritos sob a forma

 x1 = F1 (t, x1 , x2 , . . . , xn )
 ˙
 x2 = F2 (t, x1 , x2 , . . . , xn )

˙
. (5.1)
 .
 .

 x = F (t, x , x , . . . , x ).
˙ n n 1 2 n
Uma solu¸˜o do sistema de equa¸oes diferenciais (5.1) num inter-
ca c˜
valo J ´ constitu´ por n fun¸oes x1 (t), x2 (t), . . . , xn (t) que s˜o difer-
e ıda c˜ a
enci´veis em J e que satisfazem o sistema (5.1) para todo t ∈ J.
a
Exemplo 5.1. O par de fun¸oes x1 (t) = sen t e x2 (t) = cos t ´ solu¸ao
c˜ e c˜
do sistema
x1 = x2 ,
˙
x2 = −x1 .
˙
O P.V.I. para um sistema de equa¸oes diferenciais de 1a ordem ´
c˜ ¯ e
dado por:

 x1 = F1 (t, x1 , x2 , . . . , xn )
 ˙
 x2 = F2 (t, x1 , x2 , . . . , xn )
 ˙


.
.
 .
 x = F (t, x , x , . . . , x )
 ˙n
 n 1 2 n
 x (t ) = x0 , x (t ) = x0 , . . . , x (t ) = x0 ,

1 0 1 2 0 2 n 0 n
em que x0 , x0 , . . ., x0 ∈ R.
1 2 n
Existe uma importante conex˜o entre sistemas de equa¸oes dife-
a c˜
renciais e equa¸˜es de uma certa ordem: a equa¸ao de ordem n
co c˜
y (n) = F (t, y, y, . . . , y (n−1) )
˙

118. Sistemas de Equa¸˜es Diferenciais
co Cap. 5 Teoria Geral 108
pode ser transformada num sistema de n equa¸oes de c˜ 1a ordem intro-
¯
duzindo as vari´veis x1 , x2 , . . . , xn do seguinte modo.
a Sejam
x1 = y, x2 = y,
˙ x3 = y ,
¨ ..., xn = y (n−1) .
Temos que 
 x1 = x2
 ˙
 x2 = x3
 ˙


.
.
 .
 x
 ˙ n−1 = xn


 x = F (t, x , x , . . . , x ).
˙n 1 2 n
Exemplo 5.2. No sistema massa-mola, temos um sistema de duas
equa¸oes diferenciais de 2a ordem e podemos transform´-lo num sis-
c˜ ¯ a
tema de quatro equa¸oes diferenciais de 1a ordem. Definindo
c˜ ¯
z1 = x1 , z2 = x1 , z3 = x2 e z4 = x2 .
˙ ˙
Temos que


 z1
˙ = z2
m1 z2
˙ = −(k1 + k2 ) z1 + k2 z3 + F1 (t)


 z3
˙ = z4
m2 z4
˙ = k2 z1 − (k2 + k3 ) z3 + F2 (t).

Exemplo 5.3. Escreva o P.V.I.
y (4) − y = 0
y(0) = y(0) = y (0) = y (3) (0) = 0
˙ ¨
na forma de um sistema de equa¸oes diferenciais.
c˜
Solucao: Colocando x1 = y, x2 = y,
¸˜ ˙ x3 = y e x4 = y (3) , temos
¨
 
 x1 = x2
 ˙  x1 (0) = y(0) = 0

x2 = x3
˙ x2 (0) = y(0) = 0
˙
 
e
 x3 = x4
 ˙  x3 (0) = y (0) = 0
 ¨
x4 = x1
˙ x4 (0) = y (3) (0) = 0.
 

119. Sistemas de Equa¸˜es Diferenciais
co Cap. 5 Teoria Geral 109
Se cada uma das fun¸oes F1 , . . . , Fn em (5.1) for linear em x1 , . . . , xn ,
c˜
ent˜o dizemos que o sistema de equa¸oes ´ linear. O sistema mais
a c˜ e
geral de n equa¸oes lineares de 1a ordem possui a forma
c˜ ¯

 x1 = a1 1 (t) x1 + · · · + a1 n (t) xn + g1 (t)
 ˙
.
. (5.2)
 .
 x = a (t) x + · · · + a (t) x + g (t).
˙n n1 1 nn n n
Se gj (t) ≡ 0 para todo 1 ≤ j ≤ n, ent˜o dizemos que o sistema (5.2)
a
´ homogˆneo. Caso contr´rio, ele ´ n˜o homogˆneo.
e e a e a e
Evidentemente a nota¸˜o de (5.2) ´ bastante incˆmoda, ent˜o ado-
ca e o a
tamos a seguinte nota¸˜o matricial. Defina
ca
     
a1 1 (t) . . . a1 n (t) g1 (t) x1 (t)
A(t) =  . .. .  , g(t) =  .  e x(t) =  .  .
 . . 
. . .  . .  . .
an 1 (t) . . . an n (t) gn (t) xn (t)
Temos que (5.2) pode ser expresso na forma compacta
˙
x = A(t) x + g(t), [L.N.H.]
onde,
x = (x1 , . . . , x)T .
˙ ˙ ˙
Observacao 5.1. (a1 , . . . , an )T denota um vetor coluna.
¸˜
Teorema 5.1 (Existˆncia e Unicidade de Solu¸oes). Suponha que as
e c˜
fun¸˜es ai j (t) e gi (t), 1 ≤ i, j ≤ n, sejam cont´nuas num intervalo
co ı
n
J. Ent˜o dados t0 ∈ J e x0 ∈ R , existe uma unica solu¸˜o x(t) de
a ´ ca
[L.N.H.], definida em J, tal que x(t0 ) = x0 .
Observacao 5.2. Este teorema ´ uma conseq¨ˆncia (da forma ve-
¸˜ e ue
torial) do Teorema 1.1, pois temos que f (t, x) = A(t) x + g(t) e
∂(f1 , . . . , fn )
Jf = = A(t) s˜o cont´
a ınuas em J.
∂(x1 , . . . , xn )

120. Sistemas de Equa¸˜es Diferenciais
co Cap. 5 Teoria Geral 110
Teorema 5.2. Se x1 (t) = (x1 (t) . . . x1 (t)) e x2 (t) = (x2 (t) . . . x2 (t))
1 n 1 n
s˜o solu¸˜es do sistema homogˆneo
a co e
˙
x = A(t) x [L.H.]
ent˜o qualquer combina¸˜o linear c1 x1 (t) + c2 x2 (t), em que c1 e c2
a ca
s˜o constantes arbitr´rias, tamb´m ´ solu¸˜o de [L.H.]. Ou seja, o
a a e e ca
conjunto S de todas as solu¸˜es de [L.H.] ´ um espa¸o vetorial.
co e c
A demonstra¸ao deste teorema ser´ deixada como exerc´
c˜ a ıcio.
Teorema 5.3 (Teste para Independˆncia Linear). Sejam x1 (t), . . . , xk (t)
e
solu¸˜es de [L.H.] e seja t0 ∈ J. Ent˜o x1 (t), . . . , xk (t) s˜o solu¸˜es li-
co a a co
nearmente independentes se, e somente se, os vetores x1 (t0 ), . . . , xk (t0 )
s˜o linearmente independentes em Rn .
a
Demonstracao. Suponhamos que x1 (t), . . . , xk (t) sejam linear-
¸˜
mente dependentes. Ent˜o, existem constantes c1 , . . . , ck n˜o todas
a a
nulas, tais que
c1 x1 (t) + · · · + ck xk (t) = 0, para todo t ∈ J.
Logo,
c1 x1 (t0 ) + · · · + ck xk (t0 ) = 0
com constantes c1 , . . . , ck n˜o todas nulas. Portanto, x1 (t0 ), . . . , xk (t0 )
a
s˜o linearmente dependentes em Rn .
a
Reciprocamente, suponhamos que x1 (t0 ), . . . , xk (t0 ) sejam linear-
mente dependentes em Rn . Ent˜o, existem constantes c1 , . . . , ck n˜o
a a
todas nulas, tais que
c1 x1 (t0 ) + · · · + ck xk (t0 ) = 0.
Temos que a fun¸ao
c˜
ϕ(t) = c1 x1 (t) + · · · + ck xk (t),

121. Sistemas de Equa¸˜es Diferenciais
co Cap. 5 Teoria Geral 111
em que c1 , . . . , ck s˜o as constantes dadas acima, satisfaz [L.H.] pois ´
a e
uma combina¸˜o linear de solu¸oes. Al´m disso, ϕ(t0 ) = 0. Portanto,
ca c˜ e
pelo Teorema 5.1, ϕ(t) = 0 para todo t. Logo, x1 (t), . . . , xk (t) s˜o a
solu¸oes linearmente dependentes.
c˜
Teorema 5.4. A dimens˜o do espa¸o S de todas as solu¸˜es de [L.H.]
a c co
´ n.
e
Demonstracao. Vamos mostrar que [L.H.] possui n solu¸oes
¸˜ c˜
linearmente independentes. Para isto, consideremos os vetores do Rn :
e1 = (1 0 · · · 0 0)T , e2 = (0 1 0 · · · 0)T , . . ., en = (0 0 · · · 0 1)T e os
P.V.I.’s
˙
x = A(t) x
xi (t0 ) = ei , i = 1, . . . , n e t0 ∈ J.
Pelo Teorema 5.1, temos que cada P.V.I. possui uma unica solu¸˜o
´ ca
i 1 n
x (t). Como os vetores e , . . . , e s˜o linearmente independentes em
a
Rn . Logo, segue do Teorema 5.3, que x1 (t), . . . , xn (t) s˜o solu¸oes
a c˜
linearmente independentes de [L.H.].
Resta mostrar que qualquer solu¸˜o de [L.H.] pode ser escrita como
ca
1 n
combina¸˜o linear de x (t), . . . , x (t). Seja x(t) uma solu¸ao de [L.H.]
ca c˜
tal que x(t0 ) = (c1 · · · cn )T . Com estas constantes c1 , . . . , cn , cons-
tru´
ımos a fun¸ao
c˜
ϕ(t) = c1 x1 (t) + · · · + cn xn (t).
Temos que ϕ(t) satisfaz [L.H.] pois, ´ combina¸ao linear de solu¸˜es e
e c˜ co
al´m disso
e
ϕ(t0 ) = c1 x1 (t0 ) + · · · + cn xn (t0 ) = c1 e1 + c2 e2 + · · · + cn en =
= (c1 c2 . . . cn )T = x(t0 ).
Logo, pelo Teorema 5.1, ϕ(t) ≡ x(t). Portanto,
x(t) = c1 x1 (t) + · · · + cn xn (t).

122. Sistemas de Equa¸˜es Diferenciais
co Cap. 5 Teoria Geral 112
Observacao 5.3. O Teorema 5.4 diz que se conhecermos n solu¸oes
¸˜ c˜
1 n
linearmente independentes x (t), . . . , x (t) de [L.H.], ent˜o toda solu¸˜o
a ca
de [L.H.] ser´ da forma
a
x(t) = c1 x1 (t) + · · · + cn xn (t).
Por esta raz˜o, esta express˜o ´ chamada solu¸˜o geral de [L.H.].
a a e ca
Exemplo 5.4. Considere o sistema de equa¸oes diferenciais
c˜
x1 = x2
˙ 0 1
˙
ou x = x,
x2 = −x1 − 2 x2
˙ −1 −2
em que x = (x1 x2 )T . Note que o sistema procede da equa¸˜o de 2a
ca ¯
ordem
y + 2 y + y = 0,
¨ ˙
colocando x1 = y e x2 = y. Como y1 (t) = e−t e y2 (t) = t e−t s˜o duas
˙ a
solu¸oes desta equa¸˜o, temos que
c˜ ca
e−t te−t
x1 (t) = e x2 (t) =
−e−t (1 − t) e−t
s˜o duas solu¸oes deste sistema. Como x1 (0) = (1 − 1)T e x2 (0) =
a c˜
(0 1) s˜o vetores linearmente independentes em R2 , pelo Teorema
T
a
5.3, temos que x1 (t) e x2 (t) s˜o solu¸˜es linearmente independentes e
a co
pelo Teorema 5.4, toda solu¸ao deste sistema pode ser escrita sob a
c˜
forma
x1 (t) e−t te−t (c1 + t)e−t
x(t) = = c1 +c2 = .
x2 (t) −e−t (1 − t)e−t (c2 − c1 − c2 t)e−t
ıcio: Resolva o P.V.I.
Exerc´
0 1 1
˙
x= x, x(0) = .
−1 −2 1

123. Sistemas de Equa¸˜es Diferenciais
co Cap. 5 Teoria Geral 113
Definicao 5.1. Dizemos que uma matriz n × n X(t) ´ matriz
¸˜ e
ca ˙
solu¸˜o do sistema x = A(t) x, se cada coluna de X(t) ´ solu¸˜o
e ca
do sistema.
et 0
Exemplo 5.5. X(t) = ˙
´ uma matriz solu¸˜o de x =
e ca
0 e2 t
1 0
x pois,
0 2
et 0
x1 (t) = e x2 (t) =
0 e2 t
s˜o solu¸˜es de
a co
1 0
˙
x= x.
0 2
(Verifique).
Definicao 5.2. Dizemos que uma matriz n × n X(t) ´ matriz fun-
¸˜ e
˙
damental (M.F.) para o sistema x = A(t) x se X(t) ´ uma matriz
e
solu¸˜o e det X(t) = 0 para todo t no intervalo de existˆncia. Ou seja,
ca e
a co ˙
suas colunas s˜o solu¸˜es linearmente independentes de x = A(t) x.
et 0 1 0
Exemplo 5.6. X(t) = 2t ´ uma M.F. de x =
e ˙ x pois,
0 e 0 2
como vimos acima, ela ´ matriz solu¸ao e al´m disso det X(t) = e3 t = 0
e c˜ e
para todo t.
Lema 5.1. Se X(t) ´ uma M.F. de [L.H.], ent˜o a solu¸˜o geral de
e a ca
[L.H.] ser´ dada por X(t) c, em que c = (c1 · · · cn )T .
a
Demonstracao. Primeiramente, mostremos que x(t) = X(t)c ´
¸˜ e
solu¸ao de [L.H.]. De fato,
c˜
˙ ˙
x(t) = X(t) c = [A(t) X(t)] c = A(t) [X(t) c] = A(t) x(t).
Mostremos, agora, que toda solu¸˜o ´ deste tipo. Seja x(t) solu¸˜o
ca e ca
−1
de [L.H.] tal que x(t0 ) = x0 . Como a fun¸ao z(t) = X(t)[X (t0 )x0 ]
c˜

124. Sistemas de Equa¸˜es Diferenciais
co Cap. 5 Teoria Geral 114
´ solu¸˜o de [L.H.] e satisfaz z(t0 ) = x0 , pela unicidade de solu¸˜es,
e ca co
temos que z(t) = x(t). Logo,
x(t) = X(t) c, em que c = X −1 (t0 ) x0 .
Observacao 5.4. Se X(t) ´ M.F. de [L.H], isto ´, suas colunas s˜o
¸˜ e e a
solu¸oes linearmente independentes de [L.H], o lema acima afirma que
c˜
suas colunas formam uma base para o espa¸o das solu¸˜es .
c co
Teorema 5.5 (F´rmula de Jacobi-Liouville). Se X(t) ´ uma matriz
o e
solu¸˜o de [L.H.] em algum intervalo J e se t0 ∈ J, ent˜o
ca a
t
det X(t) = det X(t0 ) exp( trA(s) ds),
t0
onde trA(s) = soma dos elementos da diagonal principal de A(s).
Demonstracao. Basta notar que det X(t) satisfaz a equa¸˜o
¸˜ ca
diferencial
z = trA(t) z.
˙
Observacao 5.5. O Teorema 5.5 afirma que se X(t) ´ matriz solu¸˜o
¸˜ e ca
de [L.H.] ent˜o, ou det X(t) = 0 para todo t ∈ J ou det X(t) = 0 para
a
todo t ∈ J.
O pr´ximo teorema nos d´ um crit´rio para decidir se uma matriz
o a e
solu¸ao de [L.H.] ´ uma M.F..
c˜ e
Teorema 5.6. Seja X(t) uma matriz solu¸˜o de [L.H.] em J. X(t)
ca
´ M.F. se, e somente se, det X(t0 ) = 0 para algum t0 ∈ J.
e
Demonstracao. Suponhamos que X(t) seja M.F., ent˜o as co-
¸˜ a
lunas de X(t) s˜o solu¸oes linearmente independentes e, portanto,
a c˜
det X(t) = 0 para todo t ∈ J. Em particular, det X(t0 ) = 0 para
algum t0 ∈ J.
Reciprocamente, se det X(t0 ) = 0 para algum t0 ∈ J, pela F´rmula
o
de Jacobi-Liouville, temos que det X(t) = 0 para todo t ∈ J. Por-
tanto, X(t) ´ M.F..
e

125. Sistemas de Equa¸˜es Diferenciais
co Cap. 5 Teoria Geral 115
Exemplo 5.7. Verifique se
1 −t
 
e2 t 2
e et
X(t) =  e2 t e−t 0 
2t 7 −t
e −2 e −et
´ uma M.F. para o sistema
e
 
1 −1 0
˙
x= 1 2 1  x.
−2 1 −1
Solucao: Facilmente verifica-se que as colunas de X(t) s˜o solu¸oes
¸˜ a c˜
do sistema. Escolhendo, por simplicidade, t0 = 0, temos
1
−1 2
1
det X(0) = 1 1 0 = −3.
1 − 7 −1
2
Logo, pelo Teorema 5.4, X(t) ´ M.F..
e
t2 t
ıcios 5.1. 1) Mostre que X(t) =
Exerc´ ´ uma matriz fun-
e
2t 1
damental para o sistema
0 1
˙
x= 2 x
−2/t 2/t
em qualquer intervalo J n˜o incluindo a origem.
a
2) Verifique se ´ poss´
e ıvel determinar uma matriz A(t) cont´
ınua
para t ≥ 0, de modo que X(t) seja matriz fundamental do sistema
˙
x = A(t)x, com
t2 t 1 1+t
a) X(t) = . b) X(t) = .
t t 0 2
Em caso afirmativo construa A(t). Caso contr´rio, justifique sua res-
a
posta.

126. Sistemas de Equa¸˜es Diferenciais
co Cap. 5 Coef. Constantes 116
3) Dada a equa¸˜o diferencial t3 y (3) −3 t2 y +6 t y−6 y = 0, reduza-
ca ¨ ˙
a num sistema de equa¸˜es diferenciais de 1¯
co a ordem escrevendo-a na
˙
forma x = A(t) x e em seguida ache uma matriz fundamental de
solu¸oes para o sistema encontrado.
c˜
Sugest˜o: Determine por tentativa trˆs solu¸˜es linearmente indepen-
a e co
dentes da equa¸˜o dada.
ca
4) Considere os vetores x1 (t) = (t 1)T e x2 (t) = (t2 2 t)T .
a) Em que intervalo x1 e x2 s˜o linearmente independentes?
a
b) Que conclus˜o se pode tirar sobre os coeficientes no sistema de
a
equa¸oes diferenciais homogˆneas satisfeitas por x1 e x2 ?
c˜ e
c) Ache este sistema de equa¸oes e verifique as condi¸oes da parte
c˜ c˜
a).
5) Considere os vetores x1 (t) = (t2 2t)T e x2 (t) = (et et )T , e
responda as mesmas perguntas do Problema 4.
5.2 Sistemas Lineares com Coeficientes
Constantes
Vamos construir a solu¸ao geral do sistema
c˜
˙
x = Ax (5.3)
onde A = (ai j ), i, j = 1, 2, . . . , n ´ uma matriz constante.
e
A nossa experiˆncia com as equa¸oes de 2a ordem sugere que pro-
e c˜ ¯
curemos solu¸oes da forma
c˜
x(t) = eλ t v (5.4)
em que o n´mero λ e o vetor constante v = (v1 · · · vn )T = (0 · · · 0)T
u

127. Sistemas de Equa¸˜es Diferenciais
co Cap. 5 Coef. Constantes 117
devem ser determinados. Substituindo (5.4) no sistema (5.3), obtemos
λ eλ t v = A eλt v
ou equivalentemente
A v = λ v. (5.5)
Logo, (5.4) ´ uma solu¸ao de (5.3) se, e somente se, λ ´ um autovalor
e c˜ e
de A e v ´ um autovetor associado a λ. A equa¸˜o (5.5) ´ equivalente
e ca e
a
(A − λ I) v = 0, (5.6)
onde I ´ a matriz identidade. Para que a equa¸ao (5.6) tenha solu¸ao
e c˜ c˜
v = 0, a matriz A − λI n˜o pode ser invert´
a ıvel. Logo, devemos ter
det(A − λ I) = 0. (5.7)
Observamos que a express˜o det(A − λ I) ´ um polinˆmio de grau
a e o
n em λ, chamado polinˆmio caracter´
o ıstico de A. Assim, a equa¸˜o
ca
det(A − λ I) = 0, possui n ra´
ızes λ1 , . . . , λn que podem ser reais ou
complexas e algumas podem ter multiplicidade maior do que um.
Observacao 5.6. Se v for um autovetor de A com autovalor λ, ent˜o
¸˜ a
u = c v, em que c = 0 ´ uma constante qualquer, tamb´m ser´ um
e e a
autovetor de A com o mesmo autovalor.
Observacao 5.7. Se a matriz A for triangular, ent˜o os autovalores
¸˜ a
ser˜o os elementos da diagonal principal.
a
Temos trˆs casos a considerar:
e
1o caso: Todos os autovalores s˜o reais e distintos.
¯ a
Sejam v1 , . . . , vn os autovetores associados aos autovalores λ1 , . . . , λn ,
´
respectivamente. Como λ1 , . . . , λn s˜o distintos, segue da Algebra
a
1 n
Linear, que v , . . . , v s˜o linearmente independents. Logo, as fun¸oes
a c˜
x1 (t) = eλ1 t v1 , . . . , xn (t) = eλn t vn

128. Sistemas de Equa¸˜es Diferenciais
co Cap. 5 Coef. Constantes 118
s˜o n solu¸oes linearmente independentes de (5.3) pois, para t = 0,
a c˜
temos que os vetores
x1 (0) = v1 , . . . , xn (0) = vn
s˜o linearmente independentes. Portanto, x1 (t) = eλ1 t v1 , . . . , xn (t) =
a
eλn t vn formam uma base para o espa¸o das solu¸oes.
c c˜
Exemplo 5.8. Determine a solu¸˜o de P.V.I
ca
1 12 0
˙
x= x, x(0) = .
3 1 1
Solucao : O polinˆmio caracter´
¸˜ o ıstico da matriz dos coeficientes A ´
e
1 − λ 12
p(λ) = det(A − λ I) = = (1 − λ)2 − 36 = λ2 − 2 λ − 35.
3 1−λ
Portanto, os autovalores de A s˜o: λ1 = 7 e λ2 = −5.
a
i) λ1 = 7: Procuramos um vetor v = 0 tal que
−6 12 a 0 −6 a + 12 b = 0
(A−7 I) v = = =⇒ =⇒ a = 2 b.
3 −6 b 0 3a − 6b = 0
2 2
Logo, um autovetor ´ v1 =
e e x1 (t) = e7 t ´ uma solu¸ao.
e c˜
1 1
ii) λ2 = −5: Procuramos um vetor v = 0 tal que
6 12 a 0 6 a + 12 b = 0
(A+5 I) v = = =⇒ =⇒ a = −2 b.
3 6 b 0 3a + 6b = 0
−2
Logo, um autovetor ´ v2 =
e e uma segunda solu¸˜o ´ x2 (t) =
ca e
1
−2
e−5 t .
1

129. Sistemas de Equa¸˜es Diferenciais
co Cap. 5 Coef. Constantes 119
Como λ1 = λ2 , temos que x1 (t) e x2 (t) s˜o solu¸oes linearmente
a c˜
independentes. Ent˜o a solu¸ao geral ´
a c˜ e
2 c1 e7t − 2 c2 e−5t
x(t) = c1 x1 (t) + c2 x2 (t) = .
c1 e7 t + c2 e−5 t
Como
0 2 c1 − 2 c2 2 c1 − 2 c2 = 0 1
= x(0) = ⇒ ⇒ c1 = c2 = ,
1 c1 + c2 c1 + c2 = 1 2
temos que a solu¸ao do P.V.I. ´
c˜ e
e7 t − e−t
x(t) = .
(e7 t + e−5 t )/2
2o caso: Autovalores Complexos.
¯
Se λ = α+i β, com β = 0, ´ um autovalor de A e v = v1 +i v2 , com
e
v = 0, ´ um correspondente autovetor, ent˜o a fun¸ao z(t) = eλ t v
2
e a c˜
´ uma solu¸˜o com valores complexos do sistema (5.3). Esta solu¸ao
e ca c˜
com valores complexos d´ origem a duas solu¸˜es com valores reais,
a co
como mostra o seguinte:
Lema 5.2. Se z(t) = x(t) + i y(t) ´ uma solu¸˜o com valores com-
e ca
plexos de (5.3), ent˜o tanto x(t) como y(t) s˜o solu¸˜es reais de (5.3).
a a co
Demonstracao. Temos que
¸˜
˙ ˙ ˙
x(t) + i y(t) = z(t) = A z(t) = A [x(t) + i y(t)] = A x(t) + i A y(t).
Igualando as partes real e imagin´ria, obtemos
a
˙
x(t) = A x(t) e ˙
y(t) = A y(t).
Logo, tanto x(t) = [z(t)] como y(t) = [z(t)] s˜o solu¸oes reais de
a c˜
(5.3).

130. Sistemas de Equa¸˜es Diferenciais
co Cap. 5 Coef. Constantes 120
Escrevendo a solu¸˜o z(t) = eλ t v, em que λ = α + i β e v =
ca
1 2
v + i v , na forma
z(t) = eα t (cos β t + i sen β t)(v1 + iv2 )
= eα t [v1 cos β t − v2 sen β t + i (v1 sen β t + v2 cos β t)]
pelo Lema 5.2 temos que
x(t) = eα t (v1 cos β t − v2 sen β t)
e
y(t) = eα t (v1 sen β t + v2 cos β t)
s˜o duas solu¸oes reais de (5.3). Al´m disso, estas solu¸oes s˜o linear-
a c˜ e c˜ a
mente independentes. (Prove isto).
Exemplo 5.9. Determine uma base de solu¸oes reais para o sistema
c˜
1 −1
˙
x= x.
5 −3
Solucao : O polinˆmio caracter´
¸˜ o ıstico da matriz dos coeficientes A
2
´ p(λ) = det(A − λ I) = λ + 2 λ + 2. Portanto, os autovalores de A
e
s˜o: λ1 = −1 + i e λ2 = −1 − i. Procuremos um vetor v = 0 tal que
a
(A − λ1 I) v = 0. Ou seja
2−i −1 a 0 (2 − i) a − b = 0
= =⇒ =⇒ b = (2−i) a.
5 −2 − i b 0 5 a − (2 + i) b = 0
1
Logo, um autovetor associado a λ1 = −1 + i ´ v =
e e a fun¸ao
c˜
2−i
1 1 0
z(t) = e(−1+i) t = e−t (cos t + i sen t) +i
2−i 2 −1
e−t cos t e−t sen t
= + i −t
e−t [2 cos t + sen t] e [2 sen t − cos t]

131. Sistemas de Equa¸˜es Diferenciais
co Cap. 5 Coef. Constantes 121
´ uma solu¸ao com valores complexos. Conseq¨entemente
e c˜ u
e−t cos t
x(t) = [z(t)] =
e−t [2 cos t + sen t]
e
e−t sen t
y(t) = [z(t)] =
e−t [2 sen t − cos t]
s˜o duas solu¸oes reais linearmente independentes e, portanto, x(t) e
a c˜
y(t) formam uma base de solu¸˜es reais.
co
3o caso: Autovalores Repetidos.
¯
Se λ ´ um autovalor de multiplicidade k 1, temos duas possibi-
e
lidades:
(i) existem k autovetores linearmente independentes associados a λ;
(ii) existem menos de k autovetores linearmente independentes asso-
ciados a λ.
No caso (i) tudo se passa como quando os autovalores s˜o distintos.
a
1 k
Se v , . . . , v forem autovetores linearmente independentes associados
a λ, ent˜o eλ t v1 , . . . , eλ t vk ser˜o k solu¸oes linearmente indepedentes.
a a c˜
Exemplo 5.10. Determine uma base de solu¸oes para o sistema
c˜
 
3 2 4
˙
x = 2 0 2 x.
4 2 3
Solucao: O polinˆmio caracter´
¸˜ o ıstico da matriz dos coeficientes A
´ p(λ) = det(A − λ I) = −λ + 6 λ2 + 15 λ + 8 = 0. Portanto, os
e 3
autovalores de A s˜o: λ1 = λ2 = −1 e λ3 = 8.
a

132. Sistemas de Equa¸˜es Diferenciais
co Cap. 5 Coef. Constantes 122
(a) λ = −1 : Procuramos todos os vetores v = 0 que satisfazem
(A + I) v = 0. Ou seja,
     
4 2 4 a 0  4a + 2b + 4c = 0
2 1 2  b  = 0 =⇒ 2 a + b + 2 c = 0 =⇒ b = −2 a−2 c.
4 2 4 c 0 4a + 2b + 4c = 0

Fazendo a = 1 e c = 0, obtemos v1 = (1 − 2 0)T . Fazendo a = 0 e
c = 1, obtemos v2 = (0 − 2 1)T que s˜o dois autovetores linearmente
a
independentes associados a λ = −1. Portanto, o autovalor λ = −1 d´a
origem a duas solu¸oes linearmente independentes
c˜
   
1 0
1 −t   e x2 (t) = e−t −2 .
x (t) = e −2
0 1
(b) λ = 8: Procuramos um vetor v = 0 tal que (A − 8 I) v = 0.
Ou seja,
     
−5 2 4 a 0  −5 a + 2 b + 4 c = 0
 2 −8 2   b  = 0 ⇒ 2 a − 8 b + 2 c = 0 ⇒ a = c = 2 b.
4 2 −5 c 0 4a + 2b − 5c = 0

Logo, um autovetor ´ v3 = (2 1 2)T e, portanto,
e
 
2
3 8t  
x (t) = e 1
2
´ uma terceira solu¸˜o linearmente independente.
e ca
No caso (ii) n˜o ´ poss´ encontrar k autovetores linearmente in-
a e ıvel
dependentes associados a λ, o que significa que existem solu¸˜es de
co
(5.3) que n˜o podem ser expressas usando-se apenas fun¸˜es exponen-
a co
ciais e vetores constantes. Por analogia ao feito para equa¸oes de 2a
c˜ ¯
ordem, ´ natural procurar solu¸ao envolvendo produtos de polinˆmios
e c˜ o
e exponenciais. Ilustraremos este procedimento atrav´s do
e

133. Sistemas de Equa¸˜es Diferenciais
co Cap. 5 Coef. Constantes 123
Exemplo 5.11. Resolva o sistema
1 −1
˙
x= x.
1 3
Solucao: O polinˆmio caracter´
¸˜ o ıstico ´ p(λ) = (λ − 2)2 e, portanto
e
λ = 2 ´ autovalor de A com multiplicidade 2. Procuremos todos os
e
vetores v = 0 tais que (A − 2 I) v = 0. Ou seja,
−1 −1 a 0 −a − b = 0
= =⇒ =⇒ b = −a.
1 1 b 0 a+b=0
Portanto, todo autovetor ´ da forma v = a(1
e − 1)T . Logo, uma
solu¸ao ´
c˜ e
1
x1 (t) = e2 t
−1
e n˜o existe uma segunda solu¸ao de forma e2 t v que seja linearmente
a c˜
´
independente com x1 (t). E natural tentarmos x2 (t) = t e2 t v. Substi-
tuindo no sistema obtemos:
2 t e2 t v + e2 t v = A (t e2 t v) (5.8)
ou
e2 t [2 t v+v] = t e2 t A v =⇒ 2 t v+v−t A v = 0, para todo t ⇐⇒ v = 0
o que n˜o nos interessa.
a
Como em (5.8) aparecem termos em t e2 t e e2 t , temos que a solu¸ao,
c˜
2t 2t
al´m do termo t e v, precisa conter um termo e w. Tentemos ent˜o
e a
x2 (t) = t e2 t v + e2 t w,
em que v e w s˜o vetores constantes. Substituindo no sistema, obte-
a
mos
2 t e2 t v + e2 t (v + 2 w) = A (t e2 t v + e2 t w)

134. Sistemas de Equa¸˜es Diferenciais
co Cap. 5 Coef. Constantes 124
ou
2 t v + v + 2 w = t A v + A w.
Igualando termos em t e termos constantes, temos que v e w devem
satisfazer
Av = 2v (A − 2 I) v = 0
=⇒
Aw = v + 2w (A − 2 I) w = v.
A primeira destas equa¸˜es est´ satisfeita se v for um autovetor de A
co a
associado a λ = 2, ou seja, v = (1 − 1)T . Substituindo na segunda,
obtemos
−1 −1 w1 1 −w1 − w2 = 1
= =⇒ =⇒ w2 = −1−w1 .
1 1 w2 −1 w1 + w2 = −1
Fazendo w1 = 0, temos que w = (0 − 1)T satisfaz a segunda equa¸ao,
c˜
e portanto,
1 0 t e2 t
x2 (t) = t e2 t + e2 t =
−1 −1 −e2 t (t + 1)
´ uma segunda solu¸ao linearmente independente com x1 (t). (Prove
e c˜
este fato).
Apresentemos agora um procedimento geral para resolver o caso
(ii).
Suponhamos que A tenha k n autovetores linearmente indepen-
dentes. Ent˜o teremos apenas k solu¸oes linearmente independentes
a c˜
da forma eλt v. Para obter as n − k solu¸oes, que juntamente com
c˜
estas formem uma base para o espa¸o das solu¸˜es, devemos proceder
c co
do seguinte modo:
1) Para cada autovalor λ de A, com multiplicidade maior do que
1, procuramos solu¸˜es do tipo x(t) = t eλ t v + eλ t w, em que
co
(A − λI)v = 0
(A − λI)w = v.

135. Sistemas de Equa¸˜es Diferenciais
co Cap. 5 Coef. Constantes 125
2) Se ainda n˜o tivermos as n solu¸oes linearmente independentes,
a c˜
t2 λt
devemos procurar solu¸˜o do tipo x(t) =
ca e v + t eλ t w + eλ t u, em
2!
que 
 (A − λ I) v = 0
(A − λ I) w = v
(A − λ I) u = w.

3) Prosseguimos deste modo at´ obter as n solu¸oes linearmente
e c˜
independentes.
Exemplo 5.12. Encontrar uma base para o espa¸o das solu¸˜es de
c co
 
2 1 3
˙
x=  0 2 −1  x.
0 0 2
Solucao: O polinˆmio caracter´
¸˜ o ıstico ´ p(λ) = (2 − λ)3 e, portanto,
e
λ = 2 ´ autovalor de multiplicidade 3. Procuremos todos os vetores
e
v = 0 tais que (A − 2I)v = 0:
    
0 1 3 a 0
 0 0 −1   b  =  0  =⇒ b + 3 c = 0
−c = 0.
0 0 0 c 0
Logo, b = c = 0 e a ´ arbitr´rio. Conseq¨entemente, todo autovetor ´
e a u e
da forma v = a(1 0 0)T e, portanto,
   2t 
1 e
1 2t 
x (t) = e 0 = 0 
0 0
´ uma solu¸ao do sistema.
e c˜
Como A possui apenas um autovetor linearmente independente
associado a λ = 2, devemos procurar outra solu¸ao da forma x2 (t) =
c˜

136. Sistemas de Equa¸˜es Diferenciais
co Cap. 5 Coef. Constantes 126
t e2 t v + e2 t w, em que v ´ autovetor associado a λ = 2 e w ´ tal que
e e
(A − 2 I) w = v. Assim
    
0 1 3 w1 1
 0 0 −1   w2  =  0  =⇒ w2 + 3 w3 = 1
−w3 = 0.
0 0 0 w3 0
Logo, w2 = 1, w3 = 0 e w1 ´ arbitr´rio.
e a Portanto,
     2t 
1 0 te
x2 (t) = t e2 t  0  + e2 t  1  =  e2 t 
0 0 0
´ uma segunda solu¸˜o do sistema.
e ca
t2 2 t
´ ca a e v+t e2 t w+
A terceira e ultima solu¸˜o ser´ da forma x3 (t) =
2
e2 t u, em que v ´ autovetor associado a λ = 2, w foi determinado
e
acima e u ´ tal que (A − 2 I) u = w. Ou seja,
e
    
0 1 3 u1 0
 0 0 −1   u2  =  1  =⇒ u2 + 3 u3 = 0
−u3 = 1.
0 0 0 u3 0
Logo, u2 = 3, u3 = −1 e u1 ´ arbitr´rio. Portanto,
e a
       2 2t 
2 1 0 0 t e /2
t 2t  
x3 (t) = e 0 + t e2 t  1  + e2 t  3  =  (t + 3) e2 t 
2
0 0 −1 −e2 t
´ a terceira solu¸˜o do sistema.
e ca
Mostre que estas 3 solu¸oes s˜o linearmente independentes.
c˜ a
Exerc´ıcios 5.2. 1) a) Transforme a equa¸ao y (3) −3 y −6 y −2 y = 0,
c˜ ¨ ˙
num sistema de equa¸˜es diferenciais de 1a ordem.
co ¯
b) Calcule uma matriz fundamental para o sistema.

137. Sistemas de Equa¸˜es Diferenciais
co Cap. 5 Coef. Constantes 127
c) Dˆ a solu¸˜o geral do sistema.
e ca
d) Dˆ a solu¸˜o geral da equa¸˜o dada.
e ca ca
2) Determine uma base de solu¸˜es, uma matriz fundamental e a
co
solu¸ao geral dos sistemas abaixo:
c˜
3 −2 −3 2
˙
a) x = x. ˙
b) x = x.
2 −2 −1 −1
   
3 2 4 1 1 2
˙
c) x =  2 0 2  x. ˙
d) x =  1 2 1  x.
4 2 3 2 1 1
   
1 0 0 1 0 0
˙ = 3
e) x 1 −2  x. f) x =  2 1 −2  x.
˙
2 2 1 3 2 1
 
  −2 1 0 0
−1 −1 0  0 −2 1 0 
˙
g) x =  0 −1 ˙ 
0  x. h) x =   x.
0 0 −2 1 
0 0 −2
0 0 0 −2
3) Resolva os P.V.I.:
a) x = Ax, em que A ´ dada no exerc´ 2-h) e x(0) = (1 2 − 1 1)T .
˙ e ıcio
b) x = Ax, em que A ´ dada no exerc´ 2-g) e x(0) = (1 1 2)T .
˙ e ıcio
   
3 1 1 1
˙
c) x =  0 3 1  x, com x(0) =  0 .
0 0 2 1
e co ˙
4) Trˆs solu¸˜es de x = Ax s˜o
a
 t   t   t 
e + et e + e3 t e − e3 t
ϕ1 (t) =  e2t  , ϕ2 (t) =  e3 t  , ϕ3 (t) =  −e3 t  .
0 e3 t −e3 t

138. Sistemas de Equa¸˜es
co Cap. 5 Sistema n˜o Homogˆneo 128
a e
Determine os autovalores e os autovetores da matriz A.
˙
5) Determine se X(t) ´ uma matriz fundamental de x = Ax, para
e
alguma matriz constante A. Em caso afirmativo determine A, em que
t2 + 1 e2 t 2e−t e3 t
   
1 t+1
a) X(t) = et  1 2(t + 1) 4 t 2  b) X(t) =  2et 2e−t e3 t .
1 t+2 3 3et e−t 2e3 t
3 e2 t
 
−5 cos 2 t −5 sen 2 t
c) X(t) =  −2 (cos 2 t + sen 2 t) 2 (cos 2 t − sen 2 t) 0 .
cos 2 t sen 2 t e2 t
6) Suponha que Y (t) = X(t)C, em que X(t) e Y (t) s˜o matrizes
a
fundamentais de x˙ = Ax e C ´ uma matriz constante. Prove que
e
det C = 0.
˙
7) Seja X(t) uma matriz fundamental de x = A x e C uma matriz
constante com det C = 0. Mostre que Y (t) = X(t) C tamb´m ´ uma
e e
˙
matriz fundamental de x = A x.
5.3 ˜ ˆ
Sistemas Lineares nao Homogeneos
com Coeficientes Constantes
Consideremos o sistema linear n˜o homogˆneo
a e
˙
x = A x + g(t), [L.N.H.]
em que A ´ uma matriz n × n constante e g(t), n × 1, ´ cont´
e e ınua num
intervalo J.
O nosso objetivo ´ procurar uma solu¸˜o para [L.N.H.].
e ca
Teorema 5.7. Sejam u(t) e v(t) duas solu¸˜es quaisquer de x =
co ˙
A x + g(t). Ent˜o a sua diferen¸a ϕ(t) = u(t) − v(t)´ solu¸˜o de
a c e ca
˙ = A x.
x

139. Sistemas de Equa¸˜es
co Cap. 5 Sistema n˜o Homogˆneo 129
a e
A demonstra¸ao ser´ deixada como exerc´
c˜ a ıcio.
Teorema 5.8. Seja X(t) = (x1 (t), . . . , xn (t)) uma M.F. de x = Ax.
˙
Seja xp (t) uma solu¸˜o particular de [L.N.H.]. Ent˜o
ca a
x(t) = X(t) c + xp (t)
´ a solu¸˜o geral de [L.N.H.], em que x = (c1 · · · cn )T .
e ca
Demonstracao. Primeiramente, mostraremos que x(t) = X(t) c+
¸˜
xp (t) ´ solu¸ao de [L.N.H.]. De fato
e c˜
˙ ˙ ˙
x(t) = X(t) c + xp (t) = A X(t) c + A xp (t) + g(t)
= A [X(t) c + xp (t)] + g(t) = A x(t) + g(t).
Seja x(t) uma solu¸˜o qualquer de [L.N.H.]. Ent˜o, pelo Teorema 5.5,
ca a
temos que x(t) − xp (t) ´ solu¸ao de x = Ax. Logo,
e c˜ ˙
x(t) − xp (t) = X(t) c
e, portanto,
x(t) = X(t) c + xp (t).
Pelo Teorema 5.8, vemos que para resolver um sistema linear n˜o
a
homogˆneo precisamos saber encontrar uma solu¸˜o particular.
e ca
O m´todo dos coeficientes a determinar aplica-se sob as mes-
e
mas condi¸oes vistas para equa¸˜es de 2a ordem.
c˜ co ¯
˙
Exemplo 5.13. Determine uma solu¸ao particular para o sistema x =
c˜
t
A x + e z, em que
0 1 0
A= e z= .
8 −2 1
Solucao: p(λ) = λ2 + 2 λ − 8. Logo, os autovalores s˜o λ1 = 2 e
¸˜ a
λ2 = −4. Como n˜o existe solu¸ao do sistema homogˆneo sob a forma
a c˜ e

140. Sistemas de Equa¸˜es
co Cap. 5 Sistema n˜o Homogˆneo 130
a e
et u, tentaremos uma solu¸˜o da forma xp (t) = et v. Substituindo no
ca
sistema, obtemos
et v = A et v + et z ⇐⇒ v = A v + z ⇐⇒ (A − I) v = −z.
Portanto,
−1 1 a 0 −a + b = 0 1
= ⇒ ⇒a=b=− .
8 −3 b −1 8 a − 3 b = −1 5
Logo,
et 1
xp (t) = −
5 1
´ uma solu¸ao particular.
e c˜
˙
Exemplo 5.14. Determine uma solu¸˜o particular do sistema x =
ca
A x + e−t z, em que
1 1 −4
A= e z= .
4 1 4
Solucao : p(λ) = λ2 − 2 λ − 3. Logo, os autovalores s˜o λ1 = −1
¸˜ a
e λ2 = 3. Como existe uma solu¸˜o do sistema homogˆneo da forma
ca e
e−t u, vamos tentar uma solu¸˜o particular da forma xp (t) = e−t (v +
ca
t w), com v e w ∈ R2 . Substituindo no sistema, obtemos
e−t (−v + w − t w) = A [ e−t (v + t w) ] + e−t z
ou
−v + w − t w = A v + t A w + z.
Igualando termos em t e termos constantes, vemos que v e w devem
satisfazer
A w = −w (A + I) w = 0
=⇒
A v + u = −v + w (A + I) v = w − z.

141. Sistemas de Equa¸oes Diferenciais Cap. 5 Var. dos Parˆmetros 131
c˜ a
A primeira destas equa¸oes implica que w deve ser um (conveniente)
c˜
autovetor de A. Logo, w = α (1 − 2)T para algum α. Pondo
v = (a b)T , a segunda equa¸ao nos fornece
c˜
2 1 a α+4 2a + b = α+4
= =⇒
4 2 b −2 α − 4 4 a + 2 b = −2 α − 4.
Logo, α = −3 e b = 1 − 2 a. Pondo a = 0, obtemos b = 1. Portanto,
0 −3 −3 t e−t
xp (t) = e−t +t =
1 6 (1 + 6 t) e−t
´ uma solu¸ao particular.
e c˜
5.4 ´ ¸˜ ˆ
Metodo da Variacao dos Parametros
Outro m´todo para determinar uma solu¸ao particular do sistema
e c˜
n˜o homogˆneo ´ o M´todo da Varia¸˜o dos Parˆmetros, que ´
a e e e ca a e
˙
mais geral que o anterior, pois aplica-se tamb´m no caso x = A(t) x +
e
g(t).
Seja X(t) = (x1 (t), . . . , xn (t)) uma M.F. de x = A x. Queremos
˙
encontrar uma solu¸ao do tipo
c˜
xp (t) = X(t) u(t),
em que u(t) ´ uma fun¸ao vetorial, isto ´, u(t) = (u1 (t) · · · un (t))T .
e c˜ e
Temos
˙ ˙
xp (t) = A X(t) u(t) + X(t) u(t). (5.9)
Como xp (t) ´ solu¸ao particular do sistema n˜o homogˆneo, temos
e c˜ a e
˙
xp (t) = A xp (t) + g(t) = A X(t) u(t) + g(t). (5.10)
˙
De (5.9) e (5.10), vem que X(t) u(t) = g(t), ou
u(t) = X −1 (t) g(t).
˙

142. Sistemas de Equa¸oes Diferenciais Cap. 5 Var. dos Parˆmetros 132
c˜ a
Integrando essa express˜o de t0 a t, obtemos
a
t
u(t) = X −1 (s) g(s) ds,
t0
onde tomamos u(t0 ) = 0, pois procuramos uma solu¸ao particular.
c˜
Logo,
t
xp (t) = X(t) X −1 (s) g(s) ds.
t0
Assim temos que a solu¸ao de [L.N.H.] tal que x(t0 ) = x0 ´ dada
c˜ e
por
t
−1
x(t) = X(t) X (t0 ) x0 + X(t) X −1 (s) g(s) ds,
t0
que ´ conhecida como F´rmula da Varia¸˜o dos Parˆmetros (ou
e o ca a
f´rmula da varia¸ao das constantes).
o c˜
Exemplo 5.15. Resolver o P.V.I.
−1 0 e−t 1
˙
x= x+ , x(0) = .
0 0 1 1
Solucao: p(λ) = −λ (−1 − λ). Logo, os autovalores s˜o: λ1 = 0 e
¸˜ a
λ2 = −1.
i) λ = 0: Procuremos um vetor v = 0 tal que (A − 0I) v = 0. Ou
seja,
−1 0 a 0
= =⇒ a = 0 e b ´ arbitr´rio.
e a
0 0 b 0
Logo, v1 = (0 1)T ´ um autovetor e x1 (t) = e0t (0 1)T = (0 1)T ´
e e
uma solu¸ao.
c˜
ii) λ = −1: Procuramos um vetor v = 0 tal que (A + 1I) v = 0.
Assim
0 0 a 0
= =⇒ b = 0 e a ´ arbitr´rio.
e a
0 1 b 0

143. Sistemas de Equa¸oes Diferenciais Cap. 5 Var. dos Parˆmetros 133
c˜ a
Logo, v2 = (1 0)T ´ um autovetor e uma segunda solu¸ao ´ x2 (t) =
e c˜ e
−t T −t T
e (1 0) = (e 0) . Portanto,
0 e−t
X(t) = (x1 (t) x2 (t)) =
1 0
˙
´ uma M.F. de x = A x. Temos que
e
0 1 0 1
X −1 (t) = =⇒ X −1 (0) = .
et 0 1 0
Logo, a solu¸˜o do P.V.I. ´
ca e
t
x(t) = X(t) [X −1 (t0 ) x0 + X −1 (s) g(s) ds]
t0
−t t
0 e 0 1 1 0 1 e−s
= + ds
1 0 1 0 1 0 es 0 1
(1 + t) e−t
= .
1+t
ıcios 5.3. 1) Determine a solu¸ao geral dos sistemas abaixo:
Exerc´ c˜
2 1 1 2 −5 − cos t
˙
a) x = x+ e3 t . ˙
b) x = x+ .
3 −2 1 1 −2 sen t
   
1 2 −3 1
1 −1 −t2
˙
c) x = x+ . ˙
d) x =  1 1 2  x +  0  et .
1 3 2t
1 −1 4 −1
2) Resolva os P.V.I.’s:
   2t   
2 0 1 e 1
˙
a) x =  0 2 0  x +  0  , x(0) =  1 .
0 1 3 e2 t 1
4 5 4 et cos t 0
˙
b) x = x+ , x(0) = .
−2 −2 0 0

144. Sistemas de Equa¸oes Diferenciais Cap. 5 Var. dos Parˆmetros 134
c˜ a
2 −5 sen t 0
˙
c) x = x+ , x(0) = .
1 −2 tg t 0
3) Em cada um dos problemas abaixo, verifique que x1 (t) e x2 (t)
s˜o solu¸oes do sistema homogˆneo correspondente, e ent˜o resolva o
a c˜ e a
sistema n˜o homogˆneo. Suponha que t 0.
a e
2 −1 1 − t2
˙
a) t x = x+ ,
3 −2 2t
1 1
x1 (t) = t e x2 (t) = t−1 .
1 3
3 −2 −2 t + 2
˙
b) t x = x+ ,
2 −2 t4 + 1
1 2
x1 (t) = t−1 e x2 (t) = t2 .
2 1
0 1 cos π t
˙
c) x = x+ ,
0 −1/t 2/t2
1 ln t
x1 (t) = e x2 (t) = .
0 1/t
4) O circuito el´trico dado na figura abaixo ´ descrito pelo sistema de
e e
−1/2 −1/8 1/2
c˜ ˙
equa¸oes diferenciais x = x+ I(t),
2 −1/2 0
em que x = (x1 x2 )T , x1 ´ a corrente no indutor, x2 ´ a queda de
e e
voltagem no capacitor e I(t) ´ a corrente fornecida pela fonte externa.
e
a) Determine uma matriz fundamental X(t) para o sistema homogˆneo
e
correspondente.
b) Se I(t) = e−t/2 , determine a solu¸ao que satisfaz a condi¸˜o inicial
c˜ ca
x(0) = 0.

145. Sistemas de Equa¸˜es
co Cap. 5 Uso da Transf. de Laplace 135
I(t)
R
R L
C
5.5 ¸˜
Resolucao de Sistemas pela Trans-
formada de Laplace
A transformada de Laplace, descrita no Cap´ ıtulo 4, tamb´m se
e
aplica a resolu¸˜o de sistemas de equa¸oes diferenciais. O m´todo
` ca c˜ e
consiste em transformar um dado sistema de equa¸oes diferenciais em
c˜
um sistema de equa¸oes alg´bricas. Vamos ilustrar este procedimento
c˜ e
atrav´s de alguns exemplos.
e
Exemplo 5.16. Resolver o P.V.I.

 x = 3 y + 4 e5 t
˙
y = x − 2y
˙ (5.11)
x(0) = 1, y(0) = 0.

Solucao: Sejam X(s) = L[x(t)] e Y (s) = L[y(t)]. Aplicando trans-
¸˜
formada de Laplace a cada uma das equa¸˜es do sistema (5.11), obte-
co
mos o sistema alg´brico
e
4
sX − 1 = 3Y +
s−5
sY = X − 2Y

146. Sistemas de Equa¸˜es
co Cap. 5 Uso da Transf. de Laplace 136
cuja solu¸ao ´:
c˜ e
s+2 1 7 1
X(s) = = + ,
(s + 3) (s − 5) 8 s−5 s+3
1 1 1 1
Y (s) = = − .
(s + 3)(s − 5) 8 s−5 s+3
Logo, a solu¸˜o do P.V.I. ´
ca e
 x(t) = 1 (7 e5 t + e−3 t ),


8
 y(t) = 1 (e5 t − e−3 t ).

8
Exemplo 5.17. Resolver o P.V.I.

 x+y =0
¨
x+y =0
˙ ˙ (5.12)
x(0) = 0, x(0) = 1, y(0) = −1.
˙

Solucao: Sejam X(s) = L[x(t)] e Y (s) = L[y(t)]. Aplicando trans-
¸˜
formada de Laplace a cada uma das equa¸oes de (5.12), obtemos o
c˜
sistema alg´brico
e
s2 X + Y = 1
s X + s Y = −1,
cuja solu¸ao ´
c˜ e
1 1 1
X(s) = = − ,
s (s − 1) s−1 s
−1
Y (s) = .
s−1
Logo, a solu¸˜o do P.V.I. ´
ca e
x(t) = et − 1, y(t) = −et .
Como podemos notar no Exemplo 5.17, n˜o ´ necess´rio que as
a e a
a ordem.
equa¸oes diferenciais do sistema sejam de 1¯
c˜

147. Sistemas de Equa¸˜es
co Cap. 5 Uso da Transf. de Laplace 137
Exerc´ıcios 5.4. Usando transformada de Laplace ache a solu¸˜o de
ca
cada um dos seguintes problemas de valor inicial:
 
 x = x + 4y
˙  x = 2x − 2y
˙
1) y =x+y
˙ 2) y = −3 x + y
˙
x(0) = 3, y(0) = 2. x(0) = 5, y(0) = 0.
 
 
 x+y =0
˙ ˙  2 x + y − y = −1
˙
3) x+x+y =0
¨ 4) x − 3 x − 4 y = −1
˙
x(0) = x(0) = 0,
˙ y(0) = −2. x(0) = 2, y(0) = 1.
 

  x+x+y =0
 ¨ ˙
 x = x − y + sen 3 t
˙
3x − y = 1 + 8t
˙

5) y =x−y
˙ 6)
 x(0) = 0, x(0) = 2,
˙
x(0) = 1/3, y(0) = 0.
 
y(0) = −1.


148. Cap´
ıtulo 6
Equa¸˜es N˜o Lineares de
co a
Primeira Ordem
Estudaremos agora alguns tipos de equa¸oes diferenciais n˜o li-
c˜ a
neares. Freq¨entemente ´ conveniente escrever a equa¸ao
u e c˜
y = f (t, y)
˙
na forma
M (t, y) + N (t, y) y = 0.
˙
ıvel: basta colocar M (t, y) = −f (t, y) e N (t, y) = 1.
Isto ´ sempre poss´
e
6.1 ¸˜
Equacoes Exatas
Queremos resolver a equa¸ao diferencial (t2 + y 2 )dt + 2 t y dy = 0,
c˜
que n˜o ´ linear. Ent˜o precisamos encontrar um m´todo para resolvˆ-
a e a e e
la.
138

149. Equa¸oes N˜o Lineares
c˜ a Cap. 6 Equa¸oes Exatas
c˜ 139
¸˜ ca a
Definicao 6.1. Dada a equa¸˜o diferencial de 1¯ ordem
dy
M (t, y) + N (t, y) =0
dt
ou
M (t, y) dt + N (t, y) dy = 0, (6.1)
em que M, N : Ω → R, e Ω ´ um subconjunto aberto do R2 , dizemos
e
que (6.1) ´ uma equa¸˜o diferencial exata se existir uma fun¸˜o
e ca ca
V = V (t, y) : Ω → R tal que
∂V (t, y) ∂V (t, y)
= M (t, y) e = N (t, y)
∂t ∂y
para todo (t, y) ∈ Ω.
Exemplo 6.1. A equa¸˜o (t2 + y 2 ) dt + 2 t y dy = 0 ´ exata pois, existe
ca e
t3
V (t, y) = + t y 2 tal que
3
∂V ∂V
= t2 + y 2 = M (t, y) e = 2 t y = N (t, y).
∂t ∂y
Definicao 6.2. A fun¸˜o V (t, y) ´ chamada uma integral primeira
¸˜ ca e
de (6.1) e as curvas definidas pela equa¸˜o V (t, y) = c s˜o chamadas
ca a
curvas integrais de (6.1).
Observemos que as solu¸˜es da equa¸ao exata s˜o dadas implici-
co c˜ a
tamente por V (t, y) = c.
t3
Exemplo 6.2. No exemplo anterior, V (t, y) = + t y 2 ´ uma integral
e
3
t3
primeira da equa¸˜o dada e + t y 2 = c s˜o as curvas integrais.
ca a
3
No exemplo acima ´ f´cil ver que a equa¸ao ´ exata e achar sua
e a c˜ e
t3
solu¸ao reconhecendo que o primeiro membro ´ a diferencial de
c˜ e +
3

150. Equa¸oes N˜o Lineares
c˜ a Cap. 6 Equa¸oes Exatas
c˜ 140
t y 2 , mas, para equa¸oes mais complicadas, pode n˜o ser poss´ fazer
c˜ a ıvel
isto. O pr´ximo teorema nos fornece um crit´rio para determinar se a
o e
equa¸ao dada ´ exata ou n˜o.
c˜ e a
Teorema 6.1. Suponhamos que M, My , Mt , Ny e Nt sejam cont´nuas
ı
2
num retˆngulo R = {(t, y) ∈ R | a t b e c y d}. Ent˜o
a a
(6.1) ´ uma equa¸˜o diferencial exata se, e somente, se
e ca
∂M ∂N
= (6.2)
∂y ∂t
para todo (t, y) ∈ R.
Demonstracao. Suponhamos que (6.1) seja exata. Ent˜o existe
¸˜ a
uma fun¸ao V (t, y) tal que
c˜
∂V ∂V
=M e = N.
∂t ∂y
Assim,
∂M ∂ 2V ∂N ∂ 2V
= e = .
∂y ∂y ∂t ∂t ∂t ∂y
Como My e Nt s˜o cont´
a ınuas, segue que Vt y e Vy t s˜o cont´
a ınuas. Pelo
Teorema de Schwarz temos que
∂M ∂N
= .
∂y ∂t
Reciprocamente, se M e N satisfazem (6.2), ent˜o mostraremos
a
que (6.1) ´ exata, isto ´, vamos construir uma fun¸ao V (t, y) satis-
e e c˜
fazendo
∂V ∂V
=M e = N.
∂t ∂y
Observamos que a primeira das equa¸oes acima ´ equivalente a
c˜ e
V (t, y) = M (t, y) dt + h(y),

151. Equa¸oes N˜o Lineares
c˜ a Cap. 6 Equa¸oes Exatas
c˜ 141
onde h(y) ´ uma fun¸ao arbitr´ria de y. Derivando esta express˜o em
e c˜ a a
rela¸ao a y, obtemos
c˜
∂V (t, y) ∂M
= (t, y) dt + h (y).
∂y ∂y
∂V
Teremos que (t, y) = N (t, y) se, e somente, se
∂y
∂M
N (t, y) = (t, y) dt + h (y) (6.3)
∂y
ou
∂M
h (y) = N (t, y) − (t, y) dt.
∂y
Observamos que o segundo membro de (6.3), apesar de sua aparˆncia,
e
depende apenas de y. De fato,
∂ ∂M ∂N ∂M
N (t, y) − (t, y) dt = (t, y) − (t, y) = 0
∂t ∂y ∂t ∂y
pois, por hip´tese, M e N satisfazem (6.2). Integrando (6.3), obtemos
o
∂M
h(y) = N (t, y) − (t, y) dt dy
∂y
e, portanto,
∂M
V (t, y) = M (t, y) dt + N (t, y) − (t, y) dt dy
∂y
∂V ∂V
´ tal que
e =M e = N.
∂t ∂y
Observamos que a demonstra¸˜o do Teorema 6.1 nos fornece um
ca
m´todo para calcularmos V (t, y) e, portanto, a solu¸˜o da equa¸ao
e ca c˜
diferencial (6.1). Entretanto, ´ melhor repetir o processo cada vez que
e
for preciso do que tentarmos lembrar a express˜o de V (t, y). Note
a
tamb´m que a solu¸ao ´ obtida na forma impl´
e c˜ e ıcita, podendo ou n˜o
a
ser poss´ encontrarmos a solu¸˜o explicitamente.
ıvel ca

152. Equa¸oes N˜o Lineares
c˜ a Cap. 6 Equa¸oes Exatas
c˜ 142
Exemplo 6.3. Resolver a equa¸˜o (t2 + y 2 ) dt + 2 t y dy = 0.
ca
Solucao: Aqui M (t, y) = t2 + y 2 e N (t, y) = 2 t y. Esta equa¸ao ´
¸˜ c˜ e
exata pois, My = 2 y = Nt . Logo, existe uma fun¸ao V (t, y) tal que
c˜
(i) Vt (t, y) = t2 + y 2 e (ii) Vy (t, y) = 2 t y.
Integrando a primeira destas equa¸oes, obtemos
c˜
t3
V (t, y) = + t y 2 + h(y).
3
Derivando esta express˜o em rela¸ao a y e usando (ii), obtemos
a c˜
h (y) = 0 =⇒ h(y) = c1
e, portanto,
t3
+ t y 2 + c1 .
V (t, y) =
3
Assim, a solu¸ao desta equa¸ao diferencial ´ dada implicitamente por
c˜ c˜ e
t3 + 3 t y 2 = c.
Exemplo 6.4. Resolver o P.V.I.
y cos t + 2 t ey + (sen t + t2 ey + 2) y = 0
˙
y(0) = 1.
Solucao: Aqui M (t, y) = y cos t + 2 t ey e N (t, y) = sen t + t2 ey + 2.
¸˜
Esta equa¸˜o ´ exata, pois My = cos t + 2 t ey = Nt . Portanto, existe
ca e
uma fun¸ao V (t, y) tal que
c˜
(i) Vt (t, y) = y cos t + 2 t ey e (ii) Vy (t, y) = sen t + t2 ey + 2.
Integrando (i), obtemos
V (t, y) = y sen t + t2 ey + h(y).

153. Equa¸oes N˜o Lineares
c˜ a Cap. 6 Equa¸oes Exatas
c˜ 143
Derivando esta express˜o em rela¸ao a y e usando (ii), temos
a c˜
sen t + t2 ey + h (y) = sen t + t2 ey + 2 =⇒ h (y) = 2 =⇒ h(y) = 2 y.
Observamos que n˜o h´ necessidade de colocar constante de inte-
a a
gra¸ao em h(y) pois ela fica incorporada na solu¸ao quando escrevemos
c˜ c˜
V (t, y) = c. Portanto, as curvas integrais s˜o dadas por
a
V (t, y) = y sen t + t2 ey + 2 y = c.
Como t = 0, temos que y = 1 e c = 2. Logo, a solu¸ao do nosso P.V.I.
c˜
´ definida implicitamente pela equa¸˜o
e ca
y sen t + t2 ey + 2 y = 2.
Exerc´ ıcios 6.1. 1) Determine se cada uma das equa¸oes abaixo ´
c˜ e
exata ou n˜o. Se for exata encontre as curvas integrais
a
a) (2 t + 3) + (2 y − 2)y = 0.
˙ b) (2 t + 4 y) + (2 t − 2 y)y = 0.
˙
t dt y dy
c) (9 t2 + y − 1) − (4 y − t)y = 0. d) 2
˙ + = 0.
(t + y 2 )3/2 (t2 + y 2 )3/2
e) (et sen y − 2 y sen t) dt + (et cos y + 2 cos t) dy = 0.
f) (et sen y + 3 y) dt − (3 t − et sen y) dy = 0.
y
g) ( + 6 t) dt + (ln t − 2) dy = 0, t 0.
t
h) (2 t y 2 + 2 y) + (2 t3 y + 2 t) y = 0.
˙
i) (y et y cos 2 t − 2 et y sen 2 t + 2 t) dt + (t et y cos 2 t − 3) dy = 0.
2) Ache o valor de a que torne cada uma das seguintes equa¸oes exatas
c˜
e ent˜o resolva-as, usando este valor de a.
a
a) (t y 2 +a t2 y) dt+(t+y)t2 dy = 0. b) (y e2 t y +t) dt+a t e2 t y dy = 0.
3) Resolva cada um dos P.V.I.

154. Equa¸oes N˜o Lineares
c˜ a Cap. 6 Equa¸˜es Separ´veis
co a 144
a) 2 t y 3 + 3 t2 y 2 y = 0, y(1) = 1.
˙
b) 3 t2 + 4 t y + (2 y + 2 t2 ) y = 0, y(0) = 1.
˙
c) 3 t y + y 2 + (t2 + t y) y = 0, y(2) = 1.
˙
6.2 ¸˜ ´ ´
Equacoes com Variaveis Separaveis
Consideremos a equa¸˜o:
ca
M (t) N (y) dt + P (t) Q(y) dy = 0, (6.4)
onde P (t) = 0 para todo t e N (y) = 0 para todo y. Multiplicando
1
(6.4) por µ(t, y) = , obtemos:
P (t) N (y)
M (t) Q(y)
dt + dy = 0
P (t) N (y)
∂ M (t) ∂ Q(y)
que ´ uma equa¸˜o exata pois,
e ca ( )=0= ( ). Ent˜o as
a
∂y P (t) ∂t N (y)
curvas integrais s˜o dadas por:
a
M (t) Q(y)
V (t, y) = dt + dy = c
P (t) N (y)
que definem implicitamente a solu¸ao y(t) de (6.4).
c˜
Exemplo 6.5. Determine a solu¸˜o do P.V.I.
ca
y = t3 e−2 y
˙
y(1) = 0.
Solucao: A equa¸ao diferencial pode ser escrita na forma e2 y dy =
¸˜ c˜
3
t dt. Integrando o primeiro membro em rela¸˜o a y e o segundo em
ca
rela¸ao a t, temos
c˜
e2 y t4
= + c1 =⇒ 2 e2 y − t4 = c
2 4

155. Equa¸oes N˜o Lineares
c˜ a Cap. 6 Equa¸˜es Separ´veis
co a 145
que define implicitamente y = y(t). Neste caso podemos explicitar a
solu¸ao. Como
c˜
t4 + c t4 + c t4 + c 1/2
e2 y = =⇒ ln e2y = ln( ) =⇒ y = ln( ) .
2 2 2
Como t = 1, temos que y = 0 e c = +1. Logo, a solu¸˜o do P.V.I. ´
ca e
t4 + 1 1/2
y(t) = ln .
2
Exerc´ ıcios 6.2. 1) Resolva cada uma das equa¸oes abaixo e esta-
c˜
bele¸a as regi˜es do plano t y em que s˜o satisfeitas as condi¸˜es do
c o a co
Teorema de Existˆncia e Unicidade.
e
t2
a) y =
˙ . b) y + y 2 sen t = 0.
˙
y
t2
c) y =
˙ . d) t y = (1 − y 2 )1/2 .
˙
y (1 + t3 )
t2 t − e−t
e) y =
˙ . f) y =
˙ .
1 + y2 y + ey
2) Ache a solu¸ao, na forma expl´
c˜ ıcita, de cada P.V.I.:
2t 2t
a) y =
˙ , y(0) = −2. b) y =
˙ , y(2) = 0.
(t + t2 )y 1 + 2y
π π
c) t dt + y e−t dy = 0, y(0) = 1 d) sen 2t dt + cos 3y dy = 0, y( ) = .
2 3
y − 4t
3) Mostre que a equa¸ao y =
c˜ ˙ n˜o ´ separ´vel, mas se fizermos
a e a
t−y
y
a mudan¸a de vari´vel v = , ent˜o a equa¸ao se torna separ´vel em
c a a c˜ a
t
t e v. Ache a solu¸˜o da equa¸˜o dada usando esta t´cnica.
ca ca e

156. Equa¸oes N˜o Lineares
c˜ a Cap. 6 Fatores Integrantes 146
6.3 Fatores Integrantes
Quando uma equa¸˜o diferencial do tipo
ca
M (t, y) + N (t, y) y = 0
˙
n˜o ´ exata, naturalmente perguntamos se poder´
a e ıamos ou n˜o torn´-la
a a
exata, pela multiplica¸˜o de ambos os membros da equa¸˜o por uma
ca ca
fun¸ao conveniente.
c˜
∂M
Exemplo 6.6. A equa¸˜o y dt − t dy = 0 n˜o ´ exata, pois,
ca a e =1
∂y
∂N
e = −1. Mas, se multiplicarmos ambos os membros da equa¸ao
c˜
∂t
1
por µ(t, y) = , obtemos
ty
1 1
dt − dy = 0
t y
que ´ uma equa¸ao exata.
e c˜
Quando uma fun¸ao µ(t, y) transforma uma equa¸˜o n˜o exata do
c˜ ca a
tipo
M (t, y) + N (t, y) y = 0
˙ (6.5)
em uma equa¸˜o exata
ca
µ(t, y) M (t, y) + µ(t, y) N (t, y) y = 0
˙
dizemos que µ(t, y) ´ um fator integrante de (6.5).
e
Em geral, ´ dif´ determinarmos fatores integrantes pois, temos
e ıcil
que µ ´ fator integrante de (6.5) se, e somente, se
e
∂(µ M ) ∂(µ N ) ∂µ ∂M ∂µ ∂N
= ou M +µ =N +µ
∂y ∂t ∂y ∂y ∂t ∂t

157. Equa¸oes N˜o Lineares
c˜ a Cap. 6 Fatores Integrantes 147
que ´ uma equa¸ao bastante complicada.
e c˜
Vamos apresentar uma classe de equa¸oes diferenciais do tipo (6.5)
c˜
cujo fator integrante pode ser encontrado sem dificuldades.
Suponhamos que seja poss´ encontrar um fator integrante para
ıvel
(6.5) que seja fun¸ao s´ de t. Portanto,
c˜ o
µ(t) M (t, y) + µ(t) N (t, y) y = 0
˙
´ exata. Conseq¨entemente
e u
∂ ∂
(µ(t) M (t, y)) = (µ(t) N (t, y))
∂y ∂t
ou
∂M dµ(t) ∂N
µ(t) = N + µ(t)
∂y dt ∂t
ou
dµ(t) 1 ∂M ∂N
= − µ(t).
dt N ∂y ∂t
1 ∂M ∂N
Mas esta equa¸˜o s´ tem sentido se a express˜o
ca o a − for
N ∂y ∂t
1 ∂M ∂N
uma fun¸˜o apenas de t, isto ´,
ca e − = f (t) e, portanto,
N ∂y ∂t
temos
dµ(t)
= f (t) µ(t)
dt
que ´ uma equa¸ao linear homogˆnea de 1a ordem, cuja solu¸˜o ´
e c˜ e ¯ ca e
f (t) dt
µ(t) = e .
1 ∂N ∂M g(y) dy
Analogamente se − = g(y), ent˜o µ(y) = e
a
M ∂t ∂y
´ um fator integrante de (6.5).
e

158. Equa¸oes N˜o Lineares
c˜ a Cap. 6 Equa¸oes Homogˆneas
c˜ e 148
Exerc´ ıcios 6.3. 1) Mostre que as equa¸oes abaixo n˜o s˜o exatas,
c˜ a a
mas se tornam exatas quando multiplicadas pelo fator integrante dado.
Resolva ent˜o as equa¸˜es:
a co
a) t2 y 3 + t (1 + y 2 )y = 0, µ(t, y) = 1/t y 3 .
˙
sen y cos t + 2 e−t cos t
b) − 2e−t sen t dt + dy = 0, µ(t, y) = yet .
y y
2) Em cada um dos problemas abaixo, ache o fator integrante e resolva
a equa¸ao:
c˜
a) y = e2 t + y − 1.
˙ b) y dt + (2 t y − e−2 y ) dy = 0.
t
c) dt + ( − sen y) dy = 0. d) (3t2 y + 2ty + y 3 ) dt + (t2 + y 2 ) dy = 0.
y
3) Mostre que se (Nt − My )/(tM − yN ) = R, em que R depende
apenas de t, y, ent˜o a equa¸ao diferencial M + N y = 0 tem um fator
a c˜ ˙
integrante da forma µ(ty). Encontre a f´rmula geral para este fator
o
integrante.
6.4 ¸˜ ˆ
Equacoes Homogeneas
Definicao 6.3. Dizemos que f (t, y) ´ uma fun¸˜o homogˆnea de
¸˜ e ca e
grau n se
f (λ t, λ y) = λn f (t, y)
para todo λ = 0 e para todo (t, y) ∈ D ⊂ R2 .
Exemplo 6.7. f (t, y) = t2 − t y − y 2 ´ homogˆnea de grau 2, pois
e e
f (λ t, λ y) = λ t − λ t y − λ y = λ (t − t y − y 2 ) = λ2 f (t, y).
2 2 2 2 2 2 2
t2 − y 2
Exemplo 6.8. f (t, y) = ´ homogˆnea de grau zero pois,
e e
t2 + y 2
λ2 (t2 − y 2 )
f (λt, λy) = = λ0 f (t, y).
λ2 (t2 + y 2 )

159. Equa¸oes N˜o Lineares
c˜ a Cap. 6 Equa¸oes Homogˆneas
c˜ e 149
Definicao 6.4. Dizemos que a equa¸˜o diferencial
¸˜ ca
M (t, y)
M (t, y) + N (t, y) y = 0
˙ ou y=−
˙
N (t, y)
´ homogˆnea se as fun¸˜es M (t, y) e N (t, y) s˜o homogˆneas de
e e co a e
mesmo grau.
Para resolver a equa¸˜o homogˆnea
ca e
M (t, y)
M (t, y) + N (t, y) y = 0
˙ ou y=−
˙
N (t, y)
precisamos fazer a mudan¸a de vari´vel
c a
y = tv =⇒ dy = v dt + t dv
e, portanto,
M (t, y) M (t . 1, t . v)
v dt + t dv = dy = − dt = − dt =
N (t, y) N (t . 1, t . v)
tm M (1, v) M (1, v)
=− m dt = − dt
t N (1, v) N (1, v)
ou
M (1, v)
v+ dt + t dv = 0
N (1, v)
ou
1 1
dt + dv = 0
t M (1, v)
v+
N (1, v)
que ´ uma equa¸ao de vari´veis separadas.
e c˜ a
Exemplo 6.9. Resolver a equa¸˜o t2 + y 2 + 3 t y y = 0.
ca ˙
Solucao : M (t, y) = t2 + y 2 e N (t, y) = 3 t y s˜o homogˆneas de grau
¸˜ a e
2. Logo a equa¸˜o dada ´ homogˆnea. Fazendo y = t v, temos que
ca e e
dy = v dt + t dv e, portanto,
t2 + y 2 t2 + (t v)2 t2 (1 + v 2 ) 1 + v2
dy = − dt = − dt = − dt = − dt.
3ty 3 t (t v) 3 t2 v 3v

160. Equa¸oes N˜o Lineares
c˜ a Cap. 6 Homogeneiza¸˜o
ca 150
Logo,
1 + v2
v dt + t dv = − dt
3v
ou
1 1
dt + dv = 0.
t 1 + v2
v+
3v
Integrando,
dt 3v
+ dv = c.
t 4 v2 + 1
Logo,
3 4 y2
ln |t|+ ln[4 v 2 +1] = ln c =⇒ ln t8 (4 v 2 +1)3 = ln c =⇒ t8 ( 2 +1)3 = c.
8 t
6.5 ¸˜
Homogeneizacao
Casos que se reduzem a casos homogˆneos
e
dy ax + by + c
Consideremos a equa¸ao diferencial
c˜ = . Se c =
dx a x+b y+c
c = 0, ent˜o temos o caso homogˆneo.
a e
Se c = 0 ou c = 0, temos que a x + b y + c = 0 e a x + b y + c = 0
s˜o duas retas
a
(i) paralelas (distintas ou coincidentes) ou
(ii) concorrentes
No caso (i) temos
a b
a b
= 0 =⇒ a b = a b =⇒ = = k =⇒ a = ka e b = k b.
a b
a b

161. Equa¸oes N˜o Lineares
c˜ a Cap. 6 Homogeneiza¸˜o
ca 151
dy ax + by + c
Substituindo na equa¸˜o, vem que
ca = . Fazendo
dx k (a x + b y) + c
dv dy v+c
v = a x + b y, temos =a+b =a+b e, portanto,
dx dx kv + c
dv
v + c = dx
a+b
k+c
que ´ uma equa¸ao de vari´veis separadas.
e c˜ a
dy −2 x − 3 y + 1
Exemplo 6.10. Resolva a equa¸ao
c˜ = .
dx 4x + 6y − 5
−2 −3
¸˜
Solucao: = 0 =⇒ retas paralelas. Fazendo v = −2 x −
4 6
3 y, vem
dv dy v+1 −2 v − v
= −2 − 3 = −2 − 3( ) =⇒ dv = dx.
dx dx −2 v − 5 v+7
Integrando, temos
−2 v + 9 ln |v + 7| = x + c.
Logo, as curvas integrais s˜o
a
−2 (−2 x − 3 y) + 9 ln |(−2 x − 3 y) + 7| = x + c .
No caso (ii), as retas
r: ax + by + c = 0
e
s: a x + b y + c = 0
s˜o concorrentes em um ponto (x0 , y0 ). Fa¸amos uma mudan¸a no
a c c
sistema de coordenadas, tal que as duas retas passem pela origem do
novo sistema

162. Equa¸oes N˜o Lineares
c˜ a Cap. 6 Homogeneiza¸˜o
ca 152
x = ξ + x0 =⇒ dx = dξ e y T
η T r
y = η + y0 =⇒ dy = dη. d
d
Como a reta r passa por (x0 , y0 ), temos y0
d
d
ξ
E
a x0 + by0 + c = 0 e portanto d
d
d x
a x + b y + c = a (ξ + x0 ) + b (η + y0 ) + c x0 d
E
d
= a ξ + b η + a x0 + b y0 + c s
d
= a ξ + b η.
Analogamente,
a x + b y + c = a ξ + b η.
Portanto, nossa equa¸ao fica
c˜
dη aξ + bη
=
dξ a ξ+b η
que ´ uma equa¸ao homogˆnea.
e c˜ e
dy 6x − y − 5
Exemplo 6.11. Resolver a equa¸˜o
ca = .
dx 4x − y − 3
6 −1
¸˜
Solucao: = −2 = 0 =⇒ as retas s˜o concorrentes, e o
a
4 −1
ponto de intersec¸ao ´ (x0 , y0 ) = (1, 1). Fazendo a mudan¸a de vari´vel
c˜ e c a
x = ξ + 1 =⇒ dx = dξ
y = η + 1 =⇒ dy = dη
e a nossa equa¸ao fica
c˜
dη 6ξ − η
=
dξ 4ξ − η
que ´ homogˆnea. Fazendo η = ξ v temos dη = v dξ + ξ dv. Por outro
e e
6−v
lado, dη = dξ. Logo,
4−v
1 4−v
dξ + dv = 0.
ξ −v 2 + 5 v + 6

163. Equa¸oes N˜o Lineares
c˜ a Cap. 6 Homogeneiza¸˜o
ca 153
Integrando, temos
(v − 2)2
ln |ξ| + ln = ln k.
|v − 3|
Logo, as curvas integrais s˜o dadas por:
a
|ξ|(v − 2)2
= k.
|v − 3|
ıcios 6.4. 1) Encontre a solu¸ao de cada uma das equa¸˜es:
Exerc´ c˜ co
dy t+y dy t2 + t y + y 2
a) = . b) = .
dt t dt t2
dy 4y − 3t
c) = . d) (t2 + 3 t y + y 2 ) dt − t2 dy = 0.
dt 2t − y
dy 2y − t + 5 dy 4 t + 3 y + 15
e) = . f) = .
dt 2t − y − 4 dt 2t + y + 7
dy t + 3y − 5 dy t2 + 3 y 2
g) = . h) = .
dt t−y−1 dt 2ty
2) Mostre que, se M (t, y) dt + N (t, y) dy = 0 ´ uma equa¸ao ho-
e c˜
1
mogˆnea, ent˜o µ(t, y) =
e a ´ um fator integrante
e
t M (t, y) + y N (t, y)
para esta equa¸˜o.
ca
3) Use o resultado do problema 2 para resolver as equa¸oes:
c˜
a) 2 y dt − t dy = 0. b) (t2 + 3 y 2 ) dt − 2 t y dy = 0.

164. Respostas dos Exerc´
ıcios
ıcios 1.1
Exerc´
t4 t6 t2 n
1) yn (t) = t2 + + + ··· +
2! 3! n!
1 + e2
2) y1 (t) = et − 1, y2 (t) = t − et +
2
107 t t 2 t3 (1 + t) e2 t e3 t e4 t
y3 (t) = − + + + + 2 (1 − t) et + − +
48 4 2 3 2 3 16
ıcios 1.2
Exerc´
t2
1) y(t) = sen
2
ıcios 2.1
Exerc´
3 1−et
1) y(t) = e
2
ıcios 2.2
Exerc´
11 −2 t 4
1) a) y(t) = esen t b) y(t) = t +
6 6
t 150 et
c) y(t) = + d) y(t) = e−t dt + 5
2 t 1 + t2
t 2 t4 1
e) y(t) = (1 + t2 )−2 + +
2 4 4
154

165. Respostas dos Exerc´
ıcios Respostas 155
3 2 5 3/2
2) a) y(t) = (1 + c et )−1/3 b) y(t) = ±(c t2 + t)
9
31 8 −1/4
c) y(t) = (2 t10 − t)
16
4
4) a) y(t) = e−t4 /4 (c + t2 e−t /4 dt)−1 + t
1 1
b) y(t) = 1 + −t
c) y(t) = −t
+ et
−t + 1 + c e 1 + ce
1
d) y(t) = t − 1 + −t2
c e + 1/2
Exerc´ ıcios 2.3
mg 24 ln 100
1) v(t) = (1 − e−αt/m ) 3) T =
k ln 2
4) a) t = 40 min b) y(40) = 49.600 g
ıcios 3.1
Exerc´
√
3 t
1) b) W [y1 , y2 ](t) = − 2 , W [y1 , y2 ](t) −→ ∞ quando t → 0
√ 2t
c) y(t) = 2 t
ıcios 3.2
Exerc´
1
1) y2 (t) = e−2 t 2) y2 (t) = t et 3) y2 (t) = , t = 0
t
1 1
4) y2 (t) = , t = 0 5) y2 (t) = 2
t t
Exerc´ ıcios 3.3
1) a) y(t) = c1 e−t + c2 e2 t b) y(t) = c1 + c2 e7 t
c) y(t) = c1 cos 2 t + c2 sen 2 t d) y(t) = e2 t (c1 cos 3t + c2 sen 3t)
e) y(t) = e2 t (c1 + c2 t) f) y(t) = c1 t + c2
3) a) y(t) = c1 cos(ln t) + c2 sen(ln t)

166. Respostas dos Exerc´
ıcios Respostas 156
√ √
1 7 7
b) y(t) = √ [c1 cos ln t + c2 sen ln t]
t 2 2
ıcios 3.4
Exerc´
4 1 t
1) a) yp (t) = cos t − sen t b) yp (t) = sen 2 t
17 17 4
1 t t2 t2
c) yp (t) = t ( − + ) et d) yp (t) = + e−t
4 4 6 2
1 1 t
e) yp (t) = + (cos 2 t − 4 sen 2 t) f) yp (t) = (sen 2 t − 2 t cos 2 t)
5 17 16
1 t
g) yp (t) = − cos 3 t + sen t h) yp (t) = t (e2 t − et )
16 4
1 t 1 t e2 t
i) yp (t) = − (cos t + 7 sen t) + ( − )
50 2 5 5
4 7/2 3 t
2) b) y(t) = (c1 + c2 t) e3 t + t e
35
ıcios 3.5
Exerc´
1) a) y(t) = c1 cos t + c2 sen t − (cos t) ln(tg t + sec t)
t t
b) y(t) = c1 e3 t + c2 e2 t + e f) y(t) = c1 t −1 + c2 t − 4
2
t4 t−2
g) y(t) = c1 t + c2 t2 + h) y(t) = c1 t + c2 t2 +
6 12
i) y(t) = c1 + c2 t2 + (2 t − 2) et
3 1/2
2) y(t) = c1 t−1/2 cos t + c2 t−1/2 sen t − t cos t
2

167. Respostas dos Exerc´
ıcios Respostas 157
t2
3) y(t) = c1 t2 + c2 t−1 + ln t
3
1 (1 + t)3
4) y(t) = c1 (1 + t)2 + c2 + t (1 + t)2 +
1+t 4
ıcios 3.6
Exerc´
1) a) I(t) = 50 e−4 t sen 3 t, Q(t) = e−4 t (−6 cos 3 t−8 sen 3 t)+6
75 25
b) I(t) = (2 cos 3 t+3 sen 3 t)− e−4 t (17 sen 3 t+6 cos 3 t),
52 52
25
Q(t) = [2 sen 3 t − 3 cos 3 t + e−4 t (3 cos 3 t + 2 sen 3 t)]
52
2) a) I(t) = cos t + 2 sen t b) I(t) = 10 (cos 5 t + sen 5 t)
1 2π √
3) Amplitude = ıodo = √
, per´ , frequˆncia = 64, 4
e
4 64, 4
−t eπ + π + 1 π
4) y(t) = −e [ cos t + sen t]
2 2

168. Respostas dos Exerc´
ıcios Respostas 158
ıcios 3.7
Exerc´
t −4 t
1) a) y(t) = c1 e + c2 e
b) y(t) = (c1 + c3 t) cos t + (c2 + c4 t) sen t
c) y(t) = c et + c e−t + c e2 t
1 2 3
d) y(t) = (c1 + c2 t + c3 t 2 ) e2 t + c4 e−t
e) y(t) = c1 + c2 e2 t + c3 e−3 t
f) y(t) = c1 et − e−t (c2 cos 2 t + c3 sen 2 t)
g) y(t) = c1 cos 2 t + c2 sen 2 t + t (c3 cos 2 t + c4 sen 2 t)
h) y(t) = c1 + c2 t + e−t (c3 cos 2 t + c4 sen 2 t)
2
2) a) y(t) = −3 − 2 t − t + (3 − t) et
2
7 e 2t
4e−3 t
b) y(t) = + −
6 10 15
c) y(t) = 2 − 2 cos t + sen t
d) y(t) = c1 + c2 t + c3 et + c4 e−t + c5 cos t + c6 sen t
3) y1 (t) = t2 , y2 (t) = t3 e y3 (t) = t−2
4) y(t) = et (c1 + c2 cos t + c3 sen t) + c4 e−t
ıcios 3.8
Exerc´
t −t
1) a) y(t) = c1 et + c2 t et + c3 e−t + e +3
2
t
b) y(t) = c1 e−t + c2 cos t + c3 sen t + e−t + 4 (t − 1)
2
√ √
t −t/2 3 3
c) y(t) = c1 e + e (c2 cos t + c3 sen t)
2 2
d) y(t) = c1 + c2 cos t + c3 sen t + 1 − cos t − ln(cos t) −
− (sen t) ln(sec t + tg t)

169. Respostas dos Exerc´
ıcios Respostas 159
t −2 t 1
e) y(t) = c1 + c2 e2 t + c3 e−2 t + (e − 1) − sen t
4 5
2
t 1 t
f) y(t) = (c1 + c3 t) cos t + (c2 + c4 t) sen t + [( − ) cos t
4 2 3
3 t t2
+ ( + − ) sen t]
4 6 12
3 t2
2) a) y(t) = (1 − cos 2 t) +
16 8
3t
b) y(t) = (t − 4) cos t − ( + 4) sen t + 3 t + 4
2
11 5 cos t t
c) y(t) = et − e−t + + 2 sen t − 3 t − sen t
8 8 4 4
1 2
d) y(t) = 1 + (t + 3 t) − t et
4
ıcios 3.9
Exerc´
2 t3 t
1) a) yp (t) = − t3 − 4 t b) yp (t) = e
3 6
t −2 t sen t t −t
c) yp (t) = (e − 1) − d) yp (t) = t − 1 + e
4 5 2
t2 1 t 3 t t2
e) yp (t) = [ ( − ) cos t + ( + − ) sen t ]
4 2 3 4 6 12
1
f) yp (t) = e4 t
6
Exerc´ ıcios 4.1
1) a), b) e d) convergem c) diverge
ıcios 4.2
Exerc´

170. Respostas dos Exerc´
ıcios Respostas 160
(2 s2 − 3 s + 2) 4s 10 2
1) a) b) − 2 c)
s3 s2 +9 s +4 (s − 3)2
2 s3 − 150 s 6, (s − 2) 1 − e−π s
d) e) f)
(s2 + 25)3 [(s − 2)2 + 9]2 s
Exerc´ıcios 4.3
e−2 t sen 3 t
1) 2) e3 t cos t + 3 e3 t sen t
3
3) et (cos 3 t + 2 sen 3 t) 4) t e4 t
1 + e−2 t
5) t sen 3 t 6)
2
3 (e3 t − e−3 t)
7) 3 t et − 3 et + 3 cos t 8) 1 +
2
9) cos 2 t + sen 2 t − 1
ıcios 4.4
Exerc´
1) a) 3 cos t + sen t b) et + e3 t
sen 3 t 5 + e−t − 13 et + 7 e2 t
c) 2 cos 3 t + (t − 2) d)
6 2
2) a) c1 et + c2 t et − sen t b) e−t (c1 sen 2 t + c2 cos 2 t + 2 sen t)
ıcios 4.5
Exerc´
e−π s − e−2 π s 1 + 2 e−s − 3 e−4 s
1) a) b)
s2 s
π
2) a) (t − 2) u2 (t) b) uπ / 2 (t) cos(t − )
2
ıcios 4.6
Exerc´
1 − e−5 t − 5 t e−5 t
1) a) e4 t − e3 t c) t et d)
25
5 t3
2) a) 5 t + b) 2 sen 2 t
6

171. Respostas dos Exerc´
ıcios Respostas 161
ıcios 5.1
Exerc´
2) a) N˜o, pois detX(t) = 0 para t = 0 e t = 1
a
0 1/2
b) Sim A(t) =
0 0
   
0 1 0 t t2 t3
3) x =
˙  0 0 1  = x ; X(t) =  0 2t 3 t2 
3 2
6 / t −6 / t 3 / t 0 2 6t
4) a) x1 e x2 s˜o
a .i. em todo intervalo que n˜o cont´m t = 0 .
a e
b) Pelo menos um coeficiente deve ser descont´
ınuo em t = 0 .
0 1
c) x =
˙ x
−2 t−2 2 t−1
5) a) x1 e x2 s˜o .i. em todo intervalo que n˜o cont´m t = 0
a a e
et=2
b) Deve haver menos um coeficiente descont´ ınuo em t = 0 e t = 2
 
0 1
c) x =  2 − 2 t t 2 − 2  x
˙
t2 − 2 t t2 − 2 t
ıcios 5.2
Exerc´
 
0 1 0
1)
a) x =
˙ 0 0 1 x b) y(t) = c1 e−t + c2 ea t + c3 eb t
2 6  3   −t 
c1 e ea t eb t
c) x(t) = X(t)  c2  d) X(t) =  −e−t a ea t b eb t 
√ c3 √ e−t a 2 ea t b 2 eb t
em que a = 2 + 6 e b = 2 − 6

172. Respostas dos Exerc´
ıcios Respostas 162
2) a) base: x1 (t) = (1 2)T e−t , x2 (t) = (2 1)T e2 t
e−t 2 e2 t
M.F.: ; solu¸ao geral: x(t) = c1 x1 (t) + c2 x2 (t)
c˜
2 e−t e2 t
c) base: x1 (t) = (1 − 4 1)T et ; x2 (t) = (1 0 − 1)T e−t
x3 (t) = (2 1 2)T e8 t
d) base: x1 (t) = (1 1 1)T e4 t ; x2 (t) = (1 − 2 1)T et
x3 (t) = (1 0 − 1)T e−t
e) base: x1 (t) = (2 −2 3)T et ; x2 (t) = (0 cos 2 t sen 2 t)T et ;
x3 (t) = (0 − sen 2 t cos 2 t)T et
f) base: x1 (t) = (2 −3 2)T et ; x2 (t) = (0 cos 2 t sen 2 t)T et ;
x3 (t) = (0 sen 2 t − cos 2 t)T et
g) base: x1 (t) = (0 0 1)T e−2 t ; x2 (t) = (1 0 0)T e−t
x3 (t) = (−t 1 0)T e−t
h) base: x1 (t) = (1 0 0 0)T e−2 t ; x2 (t) = (t 1 0 0)T e−2 t ;
2 3 2
x3 (t) = ( t2 t 1 0)T e−2 t ; x4 (t) = ( t6 t2 t 1)T e−2 t
3) a) x(t) = (1 0 0 0)T e−2 t + (2 t 2 0 0)T e−2 t −
2 3 2
− ( t2 t 1 0)T e−2 t + ( t6 t2 t 1)T e−2 t
b) x(t) = (0 0 2)T e−2 t + (1 0 0)T e−t + (−t 1 0)T e−t
c) x(t) = (1 0 0)T e3 t + (t 1 0)T e3 t − (0 1 − 1)T e2 t
4) Autovalores: λ1 = 1 , λ2 = 2 e λ3 = 3
Autovetores: v1 = (1 0 0)T , v2 = (1 1 0)T e v3 = (1 1 1)T

173. Respostas dos Exerc´
ıcios Respostas 163
 
16 −25 30
1 
5) c) A = 8 −6 −24 
13
0 13 26
Exerc´ıcios 5.3
√ T √7 t √ √
1) a) x(t) = c1 (1 − 2 + 7) e + c2 (1 −2− 7)T e− 7t
+
T 3t
+ (3 2) e
 
1 t−1 3 t2 + 1 t + 1
c) x(t) = c1 e2 t + c2 e2 t +  4 2 8 
−1 −t −41 t2 − t − 3
8
2
 
− c1 + c2 (−t + 1) + c3 (− t2 + t + 1) e2 t
 
  2
2
c1 + c2 t + c3 ( t2 + 1) e2 t
   
d) x(t) =   +  −2  et
   
 
2 −1
c1 + c2 t + c3 t2 e2 t
 
3 e3 t − 2 e2 t − t e2 t
 
2) a) x(t) = 
 e2 t 

3 e3 t − 2 e2 t
t cos t + 3 t sen t + sen t
b) x(t) = 2 et
−2t sen t
1
3) a) x(t) = c1 (1 1)T t + c2 (1 3)T t −1 − (2 3)T + 2 (1 3)T t −
− (1 1)T t ln t − 1 (4 3)T t 2
3
1
b) x(t) = c1 (2 1)T t 2 + c2 (1 2)T t −1 + (3 2)T t + 10 (−2 1)T t 4 −
− 1 (2 1)T
2
     1 
1 ln t 2
c1 π sen π t + (ln t) 
c) x(t) =  +
  
1
  
0 c2 2 ln t
t t