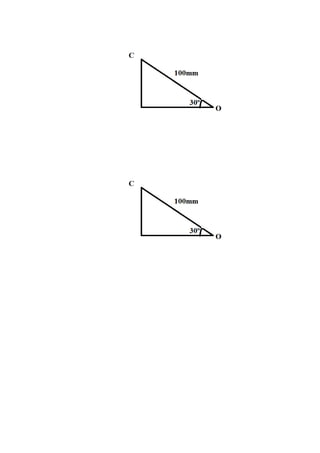
1) O ponto P se move de (50√3, 50) para (300-50√3, 0) em uma barra giratória, representando um deslocamento absoluto de 300 - 100√3 mm no eixo x. 2) Para um observador na barra, o deslocamento relativo de P é de 300 mm no eixo x, já que o observador gira junto com a barra. 3) O documento analisa o movimento de um ponto P em uma barra giratória entre dois instantes de tempo, calculando os deslocamentos absoluto e relativo a partir das posições

1. 1)
a) Fazendo uma análise do movimento temos:
i) Ponto O ( centro da esfera à esquerda ) = ( 0, 0 )
Assim, pela geometria, podemos ver que :
xc = 100cos(30) eyc = 100 sen(30). O ponto será C=( 50 √3, 50 ) no
instante inicial (to)
ii) Quando a barra CD gira de ө = 30º para ө = 150º, o ponto D está
de acordo com a seguinte figura:

2. onde O2 = (300,0), assim, O= (300-50√3, 50 ) no instante final (tf)
iii) Se P vai de C ( em to) para D ( em tf); P deslocou-se
Df – Co = ( 300 - 100√3, 0 ). Assim, o deslocamento absoluto de P é
300 - 100√3 mm no eixo x.
b) Para um observador fixo na barra CD, podemos não considerar a
rotação da barra já que tanto o observador como o ponto P sofrem a
mesma deflexão angular. Portanto o deslocamento relativo dr = Do –
Co = (300 + 50√3, 50) – (50√3, 50) = (300, 0 ) , ou seja, 300mm no
eixo x.