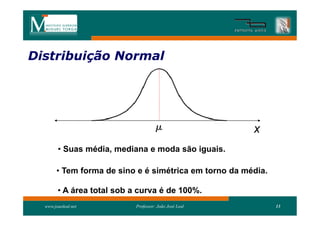
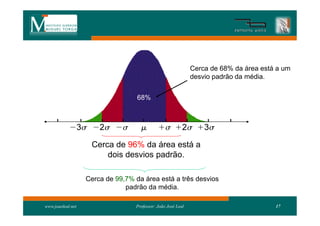
1) O documento apresenta um resumo sobre distribuições de probabilidade como Bernoulli, binomial, hipergeométrica, de Poisson e normal. 2) As distribuições de Bernoulli, binomial e de Poisson descrevem experiências aleatórias com dois resultados possíveis. 3) A distribuição normal é simétrica em torno da média e aproximadamente 68% de seus valores estão a até 1 desvio padrão da média.

1. Ano Lectivo 2009/2010
CET – Curso de Especialização Tecnológica
Métodos Computacionais e Estatísticos
Professor: João Leal

2. 2. Probabilidades
www.joaoleal.net Professor: João José Leal 2

3. Distribuição Bernoulli
Distribui
• Uma distribuição de Bernoulli resulta de um experiência
aleatória que origina apenas dois resultados possíveis:
“sucesso” e “fracasso”.
• Seja X uma v.a. com uma distribuição Bernoulli. Se p
designa a probabilidade de sucesso e a probabilidade de
falha é (1-p)=q, a função massa de probabilidade de
Bernoulli é
P ( X  0 )  (1  p )  q e P ( X  1)  p
ou
P ( X  x )  p x (1  p )1 x , x  0, 1
em que X assume o valor 1 se ocorrer sucesso e o valor 0 se
ocorrer fracasso. Escreve-se X~Bernoulli(p).
www.joaoleal.net Professor: João José Leal 3

4. • Seja X uma v.a. com distribuição Bernoulli e
probabilidade de sucesso igual a p. A média será
igual a
 X  E( X )   xP ( X  x )  (0)(1  p)  (1)p  p
X
e a variância
 X  E[( X   X ) 2 ] 
2
 X
(x   X )2 P ( X  x)
 (0  p) 2 (1  p)  (1  p) 2 p  p(1  p)
www.joaoleal.net Professor: João José Leal 4

5. • Seja X uma v.a. com distribuição Bernoulli e
probabilidade de sucesso igual a p. A média será
igual a
 X  E( X )   xP ( X  x )  (0)(1  p)  (1)p  p
X
e a variância
 X  E[( X   X ) 2 ] 
2
 X
(x   X )2 P ( X  x)
 (0  p) 2 (1  p)  (1  p) 2 p  p(1  p)
www.joaoleal.net Professor: João José Leal 5

6. Sequências de x sucessos em n
Sequên
experiências
• O número de sequências com x sucessos em n
experiências independentes é igual a:
n n!
Cx 
x!(n  x )!
onde n! = n x (n – 1) x (n – 2) x . . . x 1 e 0! = 1.
n
• Estas C x sequências são mutualmente exclusivas dado
que nenhuma das duas pode ocorrer ao mesmo tempo.
www.joaoleal.net Professor: João José Leal 6

7. Distribuição Binomial
Distribui
• Suponha que uma experiência aleatória pode resultar em
dois resultados mutualmente exclusivos e colectivamente
exaustivos, ou seja, em sucesso e fracasso. Represente-se
por p a probabilidade de sucesso em cada ensaio. Se a
experiência aleatória for repetida n vezes, a distribuição do
número de sucessos “x” é chamada de distribuição binomial.
• A função massa de probabilidade para uma v.a. binomial X =
x (sendo x = número de sucessos em n experiências
independentes):
P ( X  x )  C x p x (1  p ) ( n  x )
n
para x = 0, 1, 2 . . . , n. Escreve-se .
X ~ B (n , p )
www.joaoleal.net Professor: João José Leal 7

8. Distribuição Binomial
Distribui
• Seja X o número de sucessos de n experiências
independentes, cada uma com probabilidade de sucesso
p. Então, X segue uma distribuição binomial com média,
 X  E ( X )  np
• e variância,
 X  E [( X   X ) 2 ]  np (1  p )
2
www.joaoleal.net Professor: João José Leal 8

9. Distribuição Hipergeométrica
Distribui
• Suponha que uma amostra aleatória de n objectos é
escolhida de um grupo de N, S dos quais são sucessos. A
distribuição de número de X sucessos na amostra é
chamada de distribuição hipergeométrica. A sua função
massa de probabilidade é
S! (N  S)!

Cx Cnx
S N S
x!(S  x)! (n  x)!(N  S  n  x)!
P ( x)  
N
Cn N!
n!(N  n)!
• onde x pode tomar qualquer valor inteiro do maior de 0 e [n-
(N-S)] ao menor de n e S.
www.joaoleal.net Professor: João José Leal 9

10. Distribuição de Poisson
Distribui
Assuma que um intervalo é dividido num grande número de
subintervalos tal que a probabilidade da ocorrência de um evento
em cada subintervalo é muito pequena. Uma aplicação comum da
distribuição Poisson é fornecer a probabilidade de um certo
número de eventos ocorrerem num dado período tempo.
As hipóteses de uma distribuição de Poisson são:
 A probabilidade da ocorrência de um evento é constante para
todos os subintervalos;
 Não pode haver mais do que uma ocorrência em cada
subintervalo;
 As ocorrências são independentes; ou seja, o número de
ocorrências em intervalos sem sobreposição são independentes.
www.joaoleal.net Professor: João José Leal 10

11. • Diz-se que a v.a. X segue uma distribuição de Poisson, X
~ P(), se tem função massa de probabilidade:
e   x
P ( X  x)  , para x  0, 1,2,...
x!
onde
• P(x) é a probabilidade de x sucessos num dado
período de tempo ou espaço, dado 
•  é a taxa média de sucessos por unidade de tempo ou
espaço;  > 0
• e = 2.71828 (base do logaritmo natural)
• A média e a variância da distribuição de Poisson são:
 x  E ( X )   and  x  E[( X   ) 2 ]  
2
www.joaoleal.net Professor: João José Leal 11

12. Aproximacão da distribui
distribuição Binomial
à de Poisson
• Seja x o número de sucessos resultante de n experiências
independentes, cada uma com probabilidade de sucesso p. A
distribuição do número de sucessos X é binomial com média np.
• Se n é grande (n≥20) e p pequeno (p0.1), esta distribuição
pode ser aproximada pela distribuição de Poisson com  = np. A
função massa de probabilidade da distribuição de aproximação é
então:
e  np (np) x
P (x)  , para x  0, 1,2,...
x!
www.joaoleal.net Professor: João José Leal 12

13. Distribuição Normal
Distribui
x
• Suas média, mediana e moda são iguais.
• Tem forma de sino e é simétrica em torno da média.
• A área total sob a curva é de 100%.
www.joaoleal.net Professor: João José Leal 13

14. Ponto de inflexão Ponto de inflexão
x
• À medida que a curva se afasta da média, aproxima-se
cada vez mais do eixo x, mas nunca o toca.
• Os pontos em que a curvatura muda são chamados pontos
de inflexão. O gráfico curva-se para baixo entre os pontos
de inflexão e, para cima, à esquerda e à direita deles.
www.joaoleal.net Professor: João José Leal 14

15. Curvas com médias diferentes e o mesmo desvio padrão
10 11 12 13 14 15 16 17 18 19 20
Curvas com médias diferentes e desvios padrão diferentes
www.joaoleal.net Professor: João José Leal 15

16. Curvas com médias diferentes e desvios padrão diferentes
9 10 11 12 13 14 15 16 17 18 19 20 21 22
www.joaoleal.net Professor: João José Leal 16

17. Cerca de 68% da área está a um
desvio padrão da média.
68%
Cerca de 96% da área está a
dois desvios padrão.
Cerca de 99,7% da área está a três desvios
padrão da média.
www.joaoleal.net Professor: João José Leal 17

18. O Teorema do Limite Central
Se uma amostra de qualquer tamanho for tirada de uma
população com distribuição normal, média = e desvio
padrão =
x
a distribuição das médias da amostra de tamanho n será normal,
com média
e desvio padrão
www.joaoleal.net Professor: João José Leal 18

19. www.joaoleal.net Professor: João José Leal 19

20. www.joaoleal.net Professor: João José Leal 20

21. www.joaoleal.net Professor: João José Leal 21

22. www.joaoleal.net Professor: João José Leal 22

23. www.joaoleal.net Professor: João José Leal 23

24. www.joaoleal.net Professor: João José Leal 24

25. www.joaoleal.net Professor: João José Leal 25

27. www.joaoleal.net Professor: João José Leal 27

28. www.joaoleal.net Professor: João José Leal 28