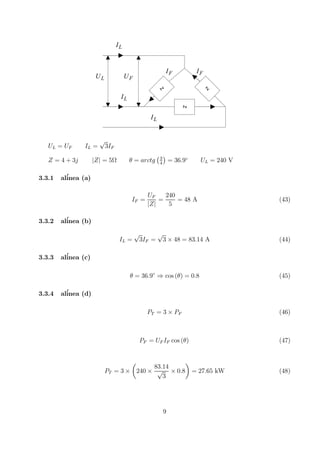
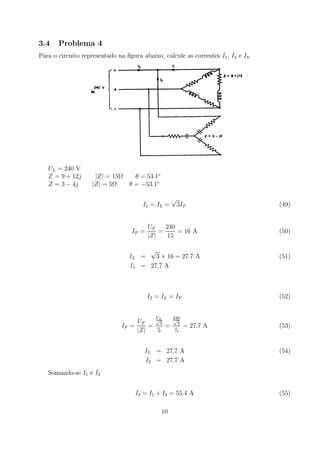
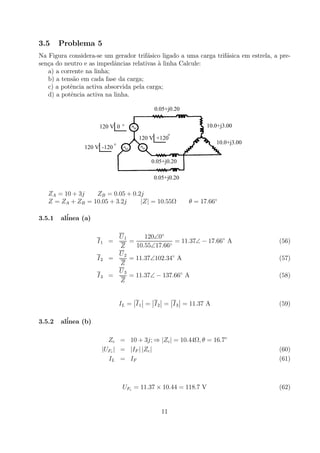
1. O documento resume 7 problemas sobre circuitos elétricos monofásicos e trifásicos. 2. Inclui cálculos de corrente, tensão, impedância e potência em circuitos com bobinas, resistores e condensadores ligados a fontes de tensão alternada. 3. Também apresenta cálculos para circuitos trifásicos com cargas em estrela e triângulo ligadas a geradores trifásicos.

1. 1 Problemas resolvidos
Sistemas Electromecˆanicos
1. Circuitos el´ectricos monof´asicos
2. Circuitos el´ectricos trif´asicos
3. Circuitos magn´eticos
4. Transformador
Paulo Branco
(2004/2005)
1

2. 2 Circuitos el´ectricos monof´asicos
2.1 Problema 1
Qual o valor da inductˆancia de uma bobina quando uma tens˜ao de 20V ´e induzida aos seus
terminais para uma mudan¸ca da corrente de 12A para 20A em 2s.
e(t) = L
di(t)
dt
⇒ dt.e(t) = L.di(t) (1)
∆t.E = L.∆I ⇒ L =
∆t
∆I
E =
2
20 − 12
× 20 = 5 H (2)
2.2 Problema 2
Uma bobina tem uma inductˆancia de 50mH. Qual a tens˜ao induzida aos seus terminais
quando a taxa de mudan¸ca da sua corrente ´e de 10000A/s ?
L = 50 µH,
∆I
∆t
= 10000 A/s
E = L.
∆I
∆t
= 50 × 10−6
× 104
= 50 × 10−2
= 0.5 V (3)
2.3 Problema 3
A bobina correspondente ao circuito prim´ario de um transformador tem uma inductˆancia
de 30mH considerando-se desprez´avel a sua resistˆencia. Calcule a sua reatˆancia para uma
frequˆencia de 60Hz e a corrente quando ligada a uma fonte de tens˜ao de 120V.
L = 30 mH, f = 60 Hz, E = 120 V
ω = 2πf = 2 × 3.146 × 60 = 377 rad/s (4)
XL = ωL = 377 × 30 × 10−3
= 11.31Ω (5)
Z = jωL ⇒ |Z| =
q
(ωL)2
= ωL ⇒ Z = 11.31Ω (6)
¯
¯I
¯
¯ = I =
E
ωL
=
120
11.31
= 10.6 A (7)
2.4 Problema 4
Um circuito com uma bobina de 0.1H e uma resistˆencia de 20Ω em s´erie s˜ao ligados a uma
fonte de tens˜ao de 100V/25Hz. Determine:
a) impedˆancia do circuito;
b) corrente;
c) tens˜ao na resistˆencia;
d) tens˜ao na bobina;
e) ˆangulo de fase da inductˆancia.
2

3. Valor instantˆaneo da tens˜ao aplicada ao circuito:
v (t) = vR (t) + vL (t) (8)
vR (t) = Ri (t) , vL (t) = L
di (t)
dt
Lei das malhas, nota¸c˜ao fasorial:
V = V R + V L = RI + jωLI (9)
V = (R + jωL) I = ZeqI
I =
V
Zeq
=
V
R + jωL
(10)
2.4.1 al´inea (a)
Zeq = 20 + jωL = 20 + 15.7j (11)
2.4.2 al´inea (b)
I =
V
Zeq
=
100∠0◦
25.42∠38.13◦
= 3.93∠ − 38.13◦
A (12)
2.4.3 al´inea (c)
V R = RI = 78.66∠ − 38.13◦
V (13)
2.4.4 al´inea (d)
V L = ZLI = (15.7∠90◦
) × (3.93∠ − 38.13◦
) = 61.7∠51.87◦
V (14)
2.4.5 al´inea (e)
αL = 90◦
(15)
2.5 Problema 5
Um condensador de 20mF e uma resistˆencia de 100Ω em s´erie s˜ao ligados a uma fonte de
tens˜ao de 120V/60Hz. Determine:
a) impedˆancia do circuito;
b) corrente;
c) tens˜ao na resistˆencia;
3

4. d) tens˜ao no condensador;
e) ˆangulo entre a corrente e a tens˜ao no condensador.
Valor instantˆaneo da tens˜ao aplicada ao circuito:
v (t) = vR (t) + vc (t) (16)
vR (t) = Ri (t) , ic (t) = C
dvc (t)
dt
Lei das malhas, nota¸c˜ao fasorial:
V = V R + V c = RI +
1
jωC
I (17)
V =
µ
R +
1
jωC
¶
I = ZeqI
I =
V
Zeq
=
V
R + 1
jωC
(18)
2.5.1 al´inea (a)
Zeq = R +
1
jωC
= R −
1
ωC
j = 100 − 132.63j Ω (19)
2.5.2 al´inea (b)
I =
V
Zeq
=
120∠0◦
166.1∠ − 52.98◦
= 0.72∠52.98◦
A (20)
2.5.3 al´inea (c)
V R = RI = 72.2∠52.98◦
V (21)
2.5.4 al´inea (d)
V c = ZcI = (132.63∠ − 90◦
) × (0.72∠52.98◦
) = 95.49∠ − 37.02◦
V (22)
2.5.5 al´inea (e)
αc = −90◦
(23)
4

5. 2.6 Problema 6
Um circuito RLC s´erie com uma resistˆencia de 50Ω, condensador de 25mF, e uma bobina
de 0.15H est´a ligado a uma fonte de tens˜ao de 120V/60Hz. Determine:
a) impedˆancia do circuito;
b) corrente;
c) tens˜ao na resistˆencia;
d) tens˜ao na bobina;
e) tens˜ao no condensador;
f) ˆangulo de fase do circuito;
g) factor de potˆencia do circuito.
2.6.1 al´inea (a)
Zeq = R + Zc + ZL = R +
1
jωC
+ jωL = (24)
= 50 + 56.55j − 106.1j = 50 − 49.55j (25)
Zeq = 70.39∠ − 44.7◦
Ω (26)
2.6.2 al´inea (b)
I =
V
Zeq
=
120∠0◦
70.4∠ − 44.7◦
= 1.7∠44.7◦
A (27)
2.6.3 al´inea (c)
V R = RI = 85.23∠44.7◦
V (28)
2.6.4 al´inea (d)
V L = ZLI = (56.55∠90◦
) × (1.7∠44.7◦
) = 96.4∠134.7◦
V (29)
2.6.5 al´inea (e)
V c = ZcI = (106.1∠ − 90◦
) × (1.7∠44.7◦
) = 180.86∠ − 45.3◦
V (30)
2.6.6 al´inea (f)
α = −44.7◦
(31)
2.6.7 al´inea (g)
f.p. = cos (α) = 0.711 (32)
5

6. 2.7 Problema 7
Uma resistˆencia de 10Ω, uma impedˆancia indutiva de 8Ω, e uma impedˆancia capacitiva de
15Ω s˜ao ligadas em paralelo numa fonte de tens˜ao de 120V/60Hz. Determine:
a) corrente total;
b) factor de potˆencia do circuito;
c) potˆencia na resistˆencia.
2.7.1 al´inea (a)
1
Zeq
=
1
R
+
1
ZL
+
1
Zc
= 10 +
1
8j
−
1
15j
= (33)
Zeq = 8.64∠30.26◦
Ω
I =
V
Zeq
=
120∠0◦
8.64∠30.26◦
= 13.89∠ − 30.26◦
A (34)
2.7.2 al´inea (b)
f.p. = cos (30.26◦
) = 0.864 (35)
2.7.3 al´inea (c)
Pact =
¯
¯V
¯
¯
¯
¯I
¯
¯ cos (30.26◦
) = 1440.7 W (36)
6

7. 3 Circuitos el´ectricos trif´asicos
3.1 Problema 1
Trˆes impedˆancias s˜ao ligadas em estrela, sendo cada uma do valor 4 − 3j. As impedˆancias
s˜ao ligadas a um gerador trif´asico equilibrado com uma tens˜ao de linha de 208V. Calcule:
a) o valor da corrente em cada impedˆancia,
b) o factor de potˆencia,
c) e a potˆencia activa total na carga.
LI
Z
Z
Z
LI
LI
FI
FI FI
FU
LU
IL = IF UL =
√
3UF
Z = 4 − 3j |Z| = 5Ω θ = arctg
¡−3
4
¢
= −36.9◦
3.1.1 al´inea (a)
IL =?
IL = IF =
UF
|Z|
=
208√
3
5
= 24 A (37)
3.1.2 al´inea (b)
Factor de potˆencia
θ = −36.9◦
⇒ cos (θ) = 0.8 (38)
7

8. 3.1.3 al´inea (c)
Potˆencia activa total
PT = 3 × PF (39)
PF = UF IF cos (θ) (40)
PT = 3 ×
208
√
3
× 24 × 0.8 = 6.92 kW (41)
3.2 Problema 2
Um gerador trif´asico com uma tens˜ao de linha no valor de 208 V est´a a alimentar uma carga
em triˆangulo. A corrente em cada impedˆancia da carga ´e de 5 A, e o factor de potˆencia ´e
de 0.8 em atraso, α < 0. Calcule a corrente na linha.
Z
Z
LI
LI
FI FI
FULU
Z
LI
IF = 5 A IL =
√
3IF
IL =
√
3 × 5 = 8.66 A (42)
3.3 Problema 3
Trˆes impedˆancias no valor de 4+3j cada uma s˜ao ligadas em triˆangulo a um gerador trif´asico
com 240 V de tens˜ao de linha. Calcule a corrente em cada fase, a corrente na linha, o factor
de potˆencia, e a potˆencia activa total na carga.
8

9. Z
Z
LI
LI
FI FI
FULU
Z
LI
UL = UF IL =
√
3IF
Z = 4 + 3j |Z| = 5Ω θ = arctg
¡3
4
¢
= 36.9◦
UL = 240 V
3.3.1 al´inea (a)
IF =
UF
|Z|
=
240
5
= 48 A (43)
3.3.2 al´inea (b)
IL =
√
3IF =
√
3 × 48 = 83.14 A (44)
3.3.3 al´inea (c)
θ = 36.9◦
⇒ cos (θ) = 0.8 (45)
3.3.4 al´inea (d)
PT = 3 × PF (46)
PF = UF IF cos (θ) (47)
PT = 3 ×
µ
240 ×
83.14
√
3
× 0.8
¶
= 27.65 kW (48)
9

10. 3.4 Problema 4
Para o circuito representado na figura abaixo, calcule as correntes I1, I2 e I3.
UL = 240 V
Z = 9 + 12j |Z| = 15Ω θ = 53.1◦
Z = 3 − 4j |Z| = 5Ω θ = −53.1◦
I1 = IL =
√
3IF (49)
IF =
UF
|Z|
=
240
15
= 16 A (50)
IL =
√
3 × 16 = 27.7 A (51)
I1 = 27.7 A
I2 = IL = IF (52)
IF =
UF
|Z|
=
UL√
3
5
=
240√
3
5
= 27.7 A (53)
IL = 27.7 A (54)
I2 = 27.7 A
Somando-se I1 e I2
I3 = I1 + I2 = 55.4 A (55)
10

11. 3.5 Problema 5
Na Figura considera-se um gerador trif´asico ligado a uma carga trif´asica em estrela, a pre-
sen¸ca do neutro e as impedˆancias relativas `a linha Calcule:
a) a corrente na linha;
b) a tens˜ao em cada fase da carga;
c) a potˆencia activa absorvida pela carga;
d) a potˆencia activa na linha.
0.05+j0.20
120 V 0 °
120 V +120°
120 V -120 °
0.05+j0.20
0.05+j0.20
10.0+j3.00
10.0+j3.00
ZA = 10 + 3j ZB = 0.05 + 0.2j
Z = ZA + ZB = 10.05 + 3.2j |Z| = 10.55Ω θ = 17.66◦
3.5.1 al´inea (a)
I1 =
U1
Z
=
120∠0◦
10.55∠17.66◦
= 11.37∠ − 17.66◦
A (56)
I2 =
U2
Z
= 11.37∠102.34◦
A (57)
I3 =
U3
Z
= 11.37∠ − 137.66◦
A (58)
IL =
¯
¯I1
¯
¯ =
¯
¯I2
¯
¯ =
¯
¯I3
¯
¯ = 11.37 A (59)
3.5.2 al´inea (b)
Zc = 10 + 3j; ⇒ |Zc| = 10.44Ω, θ = 16.7◦
|UFc | = |IF | |Zc| (60)
IL = IF (61)
UFc = 11.37 × 10.44 = 118.7 V (62)
11

12. 3.5.3 al´inea (c)
PTc = 3 (UFc IFc cos (θ)) (63)
= 3 (118.7 × 11.37 × cos (16.7))
PTc = 3.88 kW (64)
3.5.4 al´inea (d)
ZL = 0.05 + 0.2j; ⇒ |ZL| = 0.2Ω, θ = 75.96◦
|UL| = |IL| |ZL| = 11.37 × 0.2 = 2.27 V (65)
PL = 3 (ULIL cos (θ)) (66)
= 3 (2.27 × 11.37 × cos (75.96))
PL = 18 W (67)
3.6 Problema 6
Considere o gerador trif´asico representado na Figura. Cada fase do gerador debita uma
corrente de 30A com uma tens˜ao por fase de 254V e um factor de potˆencia de 0, 8. Calcule:
a) qual a tens˜ao aos terminais do gerador;
b) a potˆencia activa em cada fase;
c) a potˆencia activa total entregue pelo gerador trif´asico.
Ip = 30 A
IL = IF UL =
√
3UF
cos (θ) = 0.8
3.6.1 al´inea (a)
Tens˜ao aos terminais do gerador, UL =?
UL =
√
3UF =
√
3 × 254 = 439.9 V (68)
3.6.2 al´inea (b)
Potˆencia activa em cada fase.
PF = UF IF cos (θ) = 254 × 30 × 0.8 (69)
PF = 6.1 kW
12

13. 3.6.3 al´inea (c)
Potˆencia activa total.
PT = 3PF = 3 × 6.1 (70)
PT = 18.3 kW
3.7 Problema 7
A carga em triˆangulo representada na Figura consome uma potˆencia activa total de 600kW
para uma tens˜ao de linha de 5000V. Se a corrente medida na linha for de 75A, qual o factor
de potˆencia do circuito?
IL = 75 A
PT = 600 KW
FP = ?
α = ?
UL = UF IL =
√
3IF
PT = 600 kW UL = 5000 V IL = 75 A
PT = 3PF (71)
PT = 3 (UF IF cos (θ))
cos (θ) =
PT
3UF IF
=
600000
3 × 5000 × 75√
3
= 0.92
13