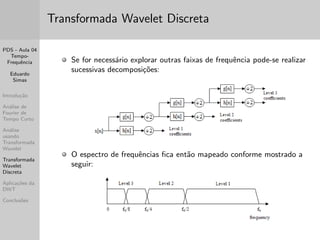
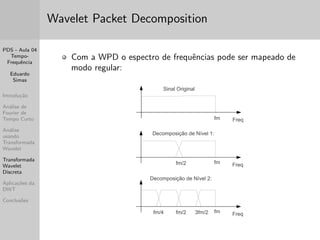
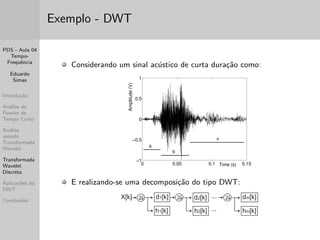
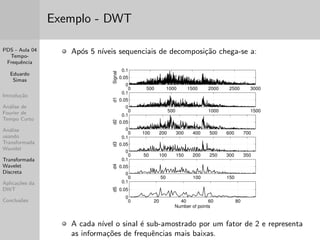
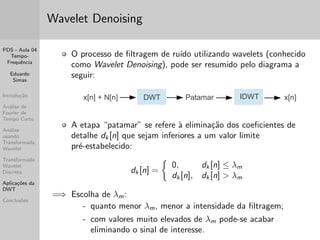
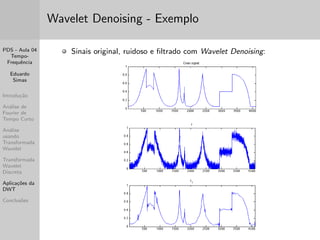
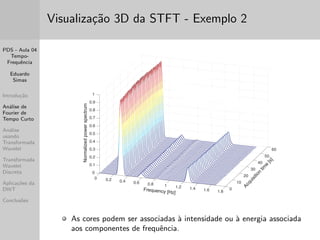
Este documento apresenta um resumo de três frases de uma aula sobre análise tempo-frequência de sinais. A aula discute transformadas de Fourier de tempo curto e wavelet, mostrando como cada uma fornece resolução diferente nos domínios do tempo e da frequência. Apresenta também exemplos práticos usando o Matlab.








![nida, no domnio
discreto como:
X(m; !) =
1X
1
x[n]f [n m]ej!n
sendo f [n] uma func~ao janela de comprimento limitado L. Ou
seja: f [n] = 0, se jnj L=2
Numa implementac~ao pratica, o deslocamento no tempo
(representado pelo par^ametro m) n~ao pode ser realizado
continuamente.
Neste caso, deve-se escolher um conjunto de valores discretos
de m usando um espacamento m pre-determinado.
Quando m L ha superposic~ao entre as janelas adjacentes.](https://image.slidesharecdn.com/pdsaula04-141202150841-conversion-gate02/85/Pds-Processamento-de-sinais-13-320.jpg)






![PDS - Aula 04
Tempo-
Frequ^encia
Eduardo
Simas
Introduc~ao
Analise de
Fourier de
Tempo Curto
Analise
usando
Transformada
Wavelet
Transformada
Wavelet
Discreta
Aplicac~oes da
DWT
Conclus~oes
Exemplos utilizando o Matlab
Para realizar analise de Fourier em janelas, o Matlab disp~oe de
rotinas nativas como o spectrogram.
Neste exemplo iremos utilizar exemplos de arquivos de audio
(musicas) e visualizar a mudanca nos componentes de frequ^encia a
medida que as musicas se desenvolvem no tempo.
Foram utilizadas as musicas a seguir (disponveis para download
juntamente com esse modulo de slides no arquivo
ExMusicasPDSaula04.mat):
- y1: Musica Carinhoso, executada pela OBMJ (Orquestra
Brasileira de Musica Jamaicana);
y2[-]: Musica I Could Have Died for You, executada pelos
Red Hot Chili Peppers.
As musicas podem ser importadas com o comando load.](https://image.slidesharecdn.com/pdsaula04-141202150841-conversion-gate02/85/Pds-Processamento-de-sinais-25-320.jpg)
![PDS - Aula 04
Tempo-
Frequ^encia
Eduardo
Simas
Introduc~ao
Analise de
Fourier de
Tempo Curto
Analise
usando
Transformada
Wavelet
Transformada
Wavelet
Discreta
Aplicac~oes da
DWT
Conclus~oes
Exemplos utilizando o Matlab
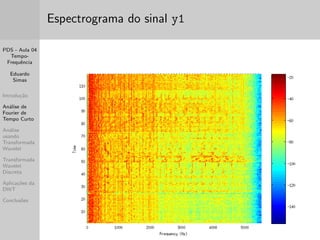
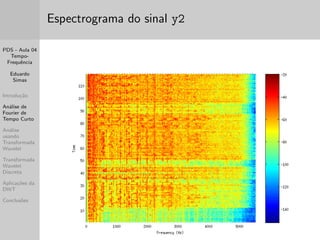
Para desenhar o espectrograma foi utilizado o comando a seguir:
figure;spectrogram(y1(1:T*fs),T*fs/100,[],Nfft,fs);, e
A sintaxe do comando garante que:
- O sinal y1 seja considerado no intervalo de 0 a T segundos;
- Sejam utilizadas janelas de Hamming com sobreposic~ao de
50 % e durac~ao T/100;
- A FFT e realizada com Nfft pontos.
Neste exemplo utilizou-se para ambos os sinais y1 e y2: T=120 e
Nfft=2048.
Recomenda-se repetir o exemplo variando-se os par^ametros acima
para veri](https://image.slidesharecdn.com/pdsaula04-141202150841-conversion-gate02/85/Pds-Processamento-de-sinais-26-320.jpg)