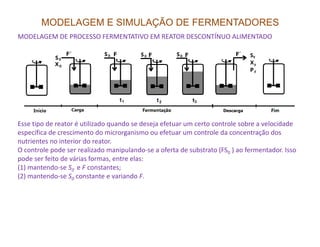
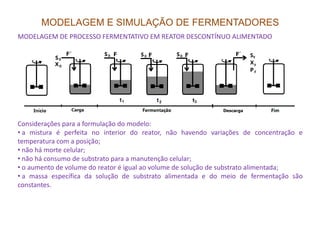
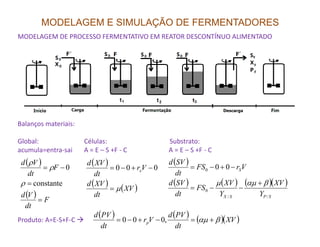
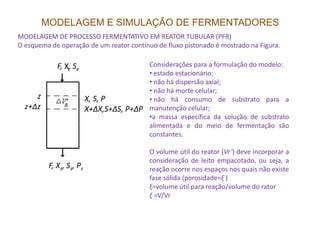
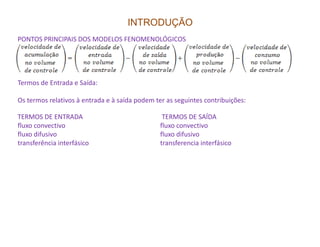
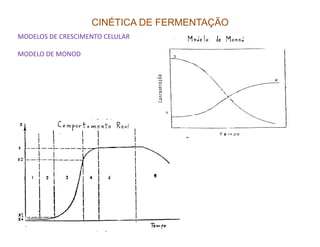
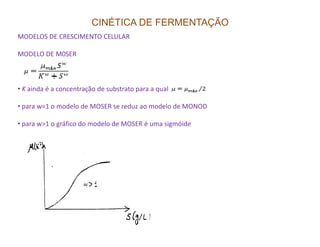
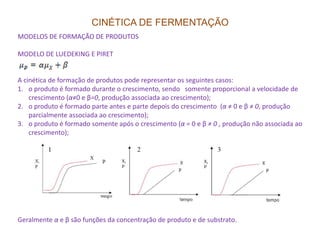
O documento discute modelagem e simulação de processos fermentativos. Aborda tópicos como modelagem matemática de processos fermentativos, simulação usando modelos matemáticos, objetivos da modelagem e simulação, interação entre população microbiana e meio de cultura, fenômenos que influenciam esta interação, diferenças entre processos químicos e fermentativos, formulação de modelos matemáticos, classificação de modelos e desenvolvimento de modelos fenomenológicos.


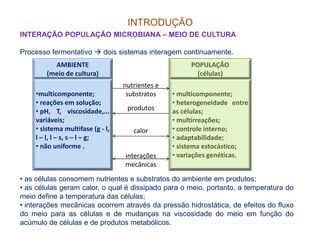


![INTRODUÇÃO
FORMULAÇÃO DE MODELOS MATEMÁTICOS EM PROCESSOS FERMENTATIVOS
É um conjunto de relações matemáticas entre as variáveis dependentes (respostas) e as
variáveis independentes (entradas) em um determinado sistema, no caso, um fermentador.
VARIÁVEIS DE RESPOSTA EM PROCESSOS FERMENTATIVOS
Concentração de microrganismo (X), substrato (S) e produto (P) ao longo do tempo e/ou espaço.
A dependência das concentrações com o tempo será determinada pela natureza estática-
dinâmica da operação do fermentador enquanto que a dependência espacial será determinadadinâmica da operação do fermentador enquanto que a dependência espacial será determinada
pelo tipo de fermentador utilizado no processo (Batelada [BSTR], Batelada alimentado [Fed-
Batch], Contínuo [CSTR] ou Tubular [PFR]).](https://image.slidesharecdn.com/mspf-160602235857/85/Mspf-6-320.jpg)
















![MODELAGEM E SIMULAÇÃO DE FERMENTADORES
FERMENTADOR EM BATELADA (BSTR)
Operação:
BALANÇO MATERIAL DA ETAPA DE FERMENTAÇÃO:
Volume de controle: volume útil do fermentador (constante).
[ACUMULA]=[entra]-[sai]+[forma]-[consumido]
Células viáveis: Células não viáveis:
Substrato: Produto:
Onde: , , , , Xd = çoncentração de células não viáveis,
r=velocidade, subscritos: d para indicar células não viáveis, x para células viáveis, s para
substrato e p para produto
dx rr
dt
dX
−= d
d
r
dt
dX
=
sr
dt
dS
−= pr
dt
dP
=
Xrx µ= Xkr dd = vpp Xr µ=vss Xr µ=](https://image.slidesharecdn.com/mspf-160602235857/85/Mspf-27-320.jpg)

![MODELAGEM E SIMULAÇÃO DE FERMENTADORES
FERMENTADOR CONTÍNUO (CSTR)
Operação:
BALANÇO MATERIAL DA ETAPA DE FERMENTAÇÃO CONTÍNUA:BALANÇO MATERIAL DA ETAPA DE FERMENTAÇÃO CONTÍNUA:
Volume de controle: volume útil do fermentador (constante).
[ACUMULA]=[entra]-[sai]+[forma]-[consumido]
Células viáveis: Células não viáveis:
Substrato: Produto:
V = volume útil do fermentador .
dx VrVrFXFX
dt
VdX
−+−= 0
sVrFSFS
dt
VdS
−−= 0 pVrFP
dt
VdP
+−=
ddd
d
VrFXFX
dt
VdX
+−= 0](https://image.slidesharecdn.com/mspf-160602235857/85/Mspf-29-320.jpg)
![MODELAGEM E SIMULAÇÃO DE FERMENTADORES
FERMENTADOR CONTÍNUO (CSTR)
Considerações comuns: ;
Estado estacionário:
Exemplo: Para o modelo de Monod
Células viáveis: Células não viáveis:
Substrato:
V
F
D =
0=
∂
∂
t
000 == dXX
dkD +=µ
( )
( ) ( )[ ]
SSD
X 0 −
=
D
Xk
X d
d =
Substrato:
Produto: Monod:
Restrições: 0 < S < S0 , 0 < X, 0 ≤ Xd ≤ X , 0 ≤ P
Passos: Cálculos na seguinte ordem S, X, P, Xd.
( ) ( )[ ] SPdSXd YkDmYkD
X
//
0
βα +++++
=
( )[ ]
D
XkD
P d βα ++
=
( )
( )dmáx
ds
kD
kDK
S
+−
+
=
µ](https://image.slidesharecdn.com/mspf-160602235857/85/Mspf-30-320.jpg)




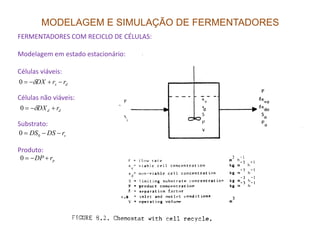
![MODELAGEM E SIMULAÇÃO DE FERMENTADORES
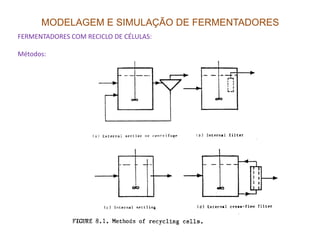
FERMENTADOR COM RECICLO DE CÉLULAS
Considerações comuns: ;
Estado estacionário:
Exemplo: Para o modelo de Monod
Células viáveis: Células não viáveis:
Substrato:
V
F
D =
0=
∂
∂
t
000 == dXX
dkD += δµ
( )
( ) ( )[ ]
SSD
X 0 −
=
D
Xk
X d
d
δ
=
Substrato:
Produto: Monod:
Restrições: 0 < S < S0 , 0 < X, 0 ≤ Xd ≤ X , 0 ≤ P
Passos: Cálculos na seguinte ordem S, X, P, Xd.
( ) ( )[ ] SPdSXd YkDmYkD
X
//
0
βδαδ +++++
=
( )[ ]
D
XkD
P d βδα ++
=
( )
( )dmáx
ds
kD
kDK
S
+−
+
=
δµ
δ](https://image.slidesharecdn.com/mspf-160602235857/85/Mspf-37-320.jpg)