Intervalos de números reais são subconjuntos do conjunto dos números reais determinados por desigualdades. Eles podem ser abertos ou fechados, representando se um número faz parte ou não do intervalo. A interseção de intervalos é o conjunto dos números que pertencem a ambos os intervalos, enquanto a reunião inclui os números que pertencem a pelo menos um dos intervalos.


![Exemplo:
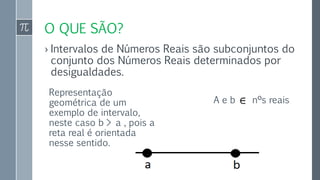
Podemos afirmar que, nesta reta o intervalo é aberto à
esquerda e fechado á direita,
]3,7] - Aberto à esquerda e fechado á direita.
3 não pertence ao intervalo, pois é aberto.](https://image.slidesharecdn.com/intervalosdensreais-171010164750/85/Intervalos-de-n-s-reais-4-320.jpg)
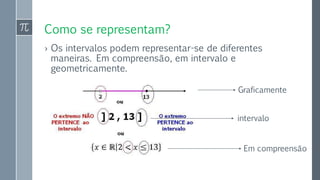
![Interseção de Intervalos Reais
› Quando temos mais do que um intervalo real é possível a
sua interseção.
› Consideremos os intervalos 3, 2A 1, 4B
Podemos afirmar que, existe interseção entre A e B ] -1 e 2
[
Graficamente
intervalo
A B Em compreensão](https://image.slidesharecdn.com/intervalosdensreais-171010164750/85/Intervalos-de-n-s-reais-6-320.jpg)
