O documento discute conceitos sobre campo elétrico, incluindo:
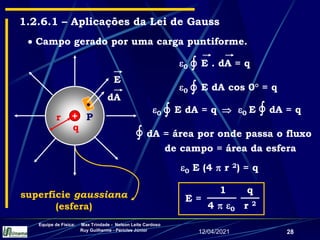
1) Campo elétrico gerado por cargas pontuais e distribuições contínuas de carga;
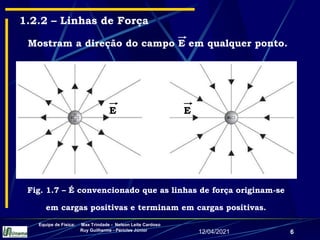
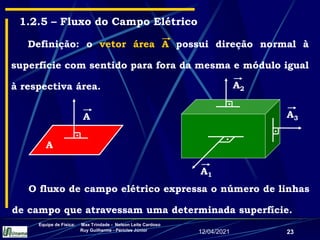
2) Linhas de campo elétrico e suas propriedades;
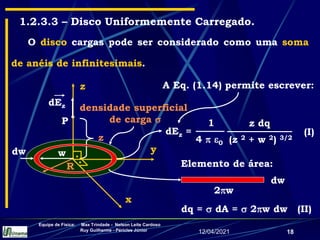
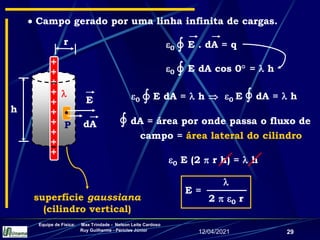
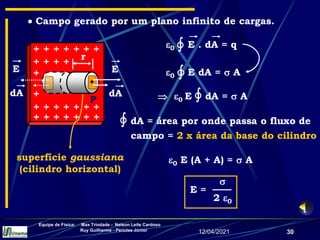
3) Expressões para o campo elétrico gerado por distribuições como linhas infinitas de carga, anéis carregados e discos carregados.


![12/04/2021
Equipe de Física: Max Trindade - Nelson Leite Cardoso
Ruy Guilherme - Péricles Júnior
4
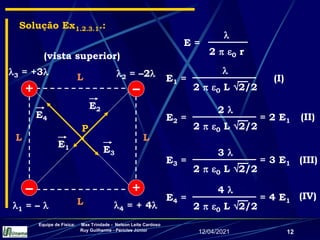
Solução Ex1.2.1.1.:
E–
x
y
+
q
–
q
P
x
d
E = E+ + E–
E+
r
E
E = E+ cos + E– cos = 2 E+ cos
De (I) em (II), vem:
E+ = E– =
1
4 0
q
r2
(I)
1
4 0
q
x2 + (d/2)2
=
(II)
d/2
x2 + (d/2)2
E = 2 E+
E = 2
d/2
x2 + (d/2)2
1
4 0
q
x2 + (d/2)2
E =
1
4 0
q d
[ x2 + (d/2)2 ]3/2](https://image.slidesharecdn.com/eletrostaticap23-210412113338/85/Eletrostatica-4-320.jpg)
![12/04/2021
Equipe de Física: Max Trindade - Nelson Leite Cardoso
Ruy Guilherme - Péricles Júnior
5
E =
1
4 0
p
x3
Definindo-se o momento de dipolo elétrico p = q d, vem:
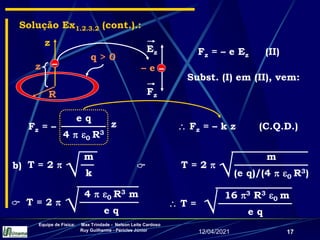
Solução Ex1.2.1.1 (cont.).:
Se x >> d, então [ x2 + (d/2)2 ]3/2 [ x2 ]3/2 = x3, logo:
E =
1
4 0
p
[ x2 + (d/2)2 ]3/2
(para um dipolo elétrico)
E
1
x3
Seguindo raciocínio semelhante para o quadrupolo, vem:
(para um quadrupolo elétrico)
E
1
x4](https://image.slidesharecdn.com/eletrostaticap23-210412113338/85/Eletrostatica-5-320.jpg)