2020 - Inteligência Artificial fuzzy.pdf

Sistemas Inteligentes
Engenharia Elétrica
Carlos Teixeira, M.Sc.
17 de março de 2020 Carlos Teixeira, M.Sc. 1

Objetivos
Visão Geral
17/03/2020 Carlos Teixeira, M.Sc. 2

Objetivos
• Principais objetivos:

Bibliografia

Bibliografia
• Livros
• 1. SHAW, IS, SIMÕES, MG, Controle e Modelagem Fuzzy, Edgard Blücher,
1999, São Paulo.

Avaliação
Critérios

Avaliação
• Provas
• 1ª prova bimestral (70 pontos):
• 2º prova bimestral (70 pontos):
• Exercícios avaliativos/trabalhos
• 1º bimestre (30 pontos): à definir
• 2º bimestre (20 pontos): à definir
• 2º bimestre (10 pontos): à confirmar (prova do colegiado)

Pré-requisitos
Noções

Pré-requisitos
• Conhecimentos básicos:
• Programação
• Lógica

Lógica Fuzzy
Definições

Lógica Fuzzy
• Introdução
• Fuzzy = Nebuloso
• Siga em frente "alguns metros"
• O dia está "parcialmente" nublado
• Preciso perder "alguns" quilos para ficar "bem"
• Usado onde as respostas “Sim” e “Não” não se encaixam adequadamente
• Aquele homem é “alto”?
• Lá fora está “quente”?

Lógica Fuzzy
• Histórico
• Conceitos “vagos” inicialmente abordados pelo lógico polonês Jan
Lukasiewicz (1878-1956) em 1920
• Introduziu conjuntos com graus de pertinência sendo 0 , ½ e 1 e, mais tarde, expandiu
para um número infinito de valores entre 0 e 1.
• Primeira publicação em 1965 por Lotfi Asker Zadeh, Berkeley (CA)
• Entre 1970 e 1980 as aplicações industriais da lógica "fuzzy" aconteceram
com maior importância na Europa e após 1980, o Japão iniciou seu uso com
aplicações na indústria.
• Por volta de 1990 é que a lógica "fuzzy" despertou um maior interesse em
empresas dos Estados Unidos.

Lógica Fuzzy
• Vantagens
• Modelagem de problemas complexos e não lineares
• Complexidade reduzida
• Menor número de regras
• Pode envolver múltiplos especialistas capaz de conciliar informações
consistentes e conflitantes
• Tratamento de incertezas de forma eficaz

Lógica Fuzzy
• Vantagens
• Precisão versus significância
1000kg
Um corpo de massa igual a
1000Kg se aproxima de sua
cabeça a 50m/s!
Saia daí!!!
50m/s

Lógica Fuzzy
• Softwares/ferramentas auxilares
• InFuzzy (desenvolvido na UNISC)
• Fuzzy Toolbox do Matlab
• NEFCON, NEFCLASS e NEFPROX... (desenvolvidos pela Universidade de
Magdeburg)
• Disponível para download em
• http://fuzzy.cs.uni-magdeburg.de/
• http://fuzzy.cs.uni-magdeburg.de/wiki/pmwiki.php?n=Forschung.Software
• SciFLT for Scilab (free)
• UnFuzzy (free)
• FuzzyTech
• FuzzyClips (free, API para Java)

Lógica Fuzzy
• Conjuntos
• Teoria Clássica
• Conjuntos ordinários (ou Crisp): noção de pertinência é bem definida
• Elemento pertencem ou não pertencem a um dado conjunto (em um universo 𝑋)
𝑓𝐴 𝑥 = ቊ
1, 𝑠𝑒 𝑒 𝑠𝑜𝑚𝑒𝑛𝑡𝑒 𝑠𝑒 𝑥 ∈ 𝐴
0, 𝑠𝑒 𝑒 𝑠𝑜𝑚𝑒𝑛𝑡𝑒 𝑠𝑒 𝑥 ∉ 𝐴
em que, 𝑓 é a função característica

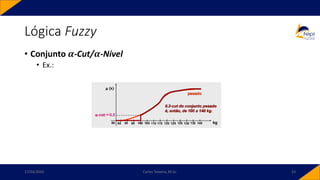
Lógica Fuzzy
• Conjuntos
• Teoria Fuzzy
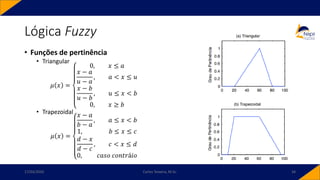
• Conjuntos Fuzzy: existe um grau de pertinência de cada elemento a um determinado
conjunto.
• Neste caso a função característica pode ser generalizada de modo que os valores
designados aos elementos do conjunto universo 𝑈 pertençam ao intervalo fechado real de
0 a 1
𝜇𝐴: 𝑈 → [0,1]
Estes valores indicam o grau de pertinência dos elementos do conjunto 𝑈 em relação ao
conjunto 𝐴, ou seja, quanto é possível para um elemento 𝑥 de 𝑈 pertencer ao conjunto 𝐴
Tal função é chamada de função de pertinência e o conjunto 𝐴 é definido como Conjunto
Fuzzy.

Lógica Fuzzy
• Conceitos
• Altura
• É o maior grau de pertinência permitido pela função de pertinência
• Normalização
• Um dado conjunto fuzzy é dito ser normal se sua altura for igual a 1
• Função normal mínima
• Pelo menos um elemento tem 𝜇 𝑥 = 1
• Função normal máxima
• Pelo menos um elemento tem 𝜇 𝑥 = 1 e outro elemento tem 𝜇 𝑥 = 0
Para um bom desempenho, os conjuntos fuzzy devem ser normalizados.

Lógica Fuzzy
• Conceitos
• Domínio
• Universo total de valores possíveis para os elementos de um conjunto
• Ex.:

Lógica Fuzzy
• Conceitos
• Suporte (área efetiva do domínio)
• O suporte de um conjunto fuzzy 𝐴 no conjunto universo 𝑈 é o conjunto clássico que
contém todos os elementos de 𝑈 que têm grau de pertinência maior do que zero
sup 𝐴 = 𝑥 ∈ 𝑈 𝜇𝐴 𝑥 > 0}
• Ex.:

Lógica Fuzzy
• Conceitos
• Suporte (área efetiva do domínio)
• O conjunto fuzzy cujo suporte é um único ponto em X, com valor de 𝜇 𝑥 = 1, é
chamado de Conjunto Singleton
• Ex.:

Lógica Fuzzy
• Conceitos
• Cardinalidade
• A cardinalidade de um conjunto fuzzy 𝐴 sobre um conjunto universo finito 𝑈 é a soma
dos graus de pertinência de todos os elementos de 𝑈 em 𝐴.
𝐴 = ෍
𝑥∈𝑈
𝜇𝐴(𝑥)
• Universo de discurso
• Espaço completo de variação de uma variável modelo
• Ex.:
• Variável modelo: TEMPERATURA
• Universo de discurso: 100 a 360

Lógica Fuzzy
• Representação
• Um conjunto fuzzy 𝐴 em 𝑈 pode ser representado como um conjunto de pares
ordenados de um elemento genérico 𝑥 e seu grau de pertinência
𝐴 = 𝜇𝐴 𝑥 /𝑥 , 𝑥 ∈ 𝑈
• Se 𝑈 for contínuo, a coleção de todos os pontos 𝑥 ∈ 𝑈 com função de pertinência
𝜇(𝑥) é denotada por
න
𝑥
(𝜇𝐴(𝑥)/𝑥)𝑑𝑥
• Se 𝑈 for discreto, a união de todos os pontos 𝑥𝑖 ∈ 𝑈 com função de pertinência
𝜇(𝑥𝑖) é denotada por
෍
𝑖=1
𝑛
𝜇𝐴(𝑥𝑖)/𝑥𝑖

Lógica Fuzzy
• Exemplo 1
• Idade
• Conjunto universo 𝑈 = {5,10,20,30,40,50,60,70,80}
• Conjuntos fuzzy
• 𝐴 = {𝑐𝑟𝑖𝑎𝑛ç𝑎𝑠}
• 𝐵 = {𝑗𝑜𝑣𝑒𝑛𝑠}
• 𝐶 = {𝑎𝑑𝑢𝑙𝑡𝑜𝑠}
• 𝐷 = {𝑣𝑒𝑙ℎ𝑜𝑠}
sup(𝑗𝑜𝑣𝑒𝑚) = {5,10,20,30,40,50}
𝑣𝑒𝑙ℎ𝑜 = 0 + 0 + 0.1 + 0.2 + 0.4 + 0.6 + 0.8 + 1 + 1 = 4.1
𝐵 =
1
5
+
1
10
+
0.8
20
+
0.5
30
+
0.2
40
+
0.1
50
+
0
60
+
0
70
+
0
80

Lógica Fuzzy
• Operações
• O conjunto fuzzy 𝐴 é um subconjunto de um conjunto fuzzy 𝐵 se o grau de
pertinência de cada elemento do conjunto universo 𝑈 no conjunto 𝐴 for
menor ou igual que seu grau de pertinência no conjunto 𝐵, ou seja, para
se ∀ 𝑥 ∈ 𝑈, 𝜇𝐴 𝑥 ≤ 𝜇𝐵 𝑥
𝐴 ⊆ 𝐵
• Os conjuntos fuzzy 𝐴 e 𝐵 são iguais se ∀ 𝑥 ∈ 𝑈, 𝜇𝐴 𝑥 = 𝜇𝐵 𝑥
𝐴 = 𝐵
• Os conjuntos fuzzy 𝐴 e 𝐵 são diferentes (não iguais), se 𝜇𝐴 𝑥 ≠ 𝜇𝐵 𝑥
para no mínimo um 𝑥 ∈ 𝑈
𝐴 ≠ 𝐵

Lógica Fuzzy
• Operações
• O conjunto fuzzy 𝐴 é um subconjunto próprio de um conjunto fuzzy 𝐵
quando 𝐴 for um subconjunto de 𝐵 e também quando forem diferentes, ou
seja, se e somente se 𝐴 ⊆ 𝐵 𝑒 𝐴 ≠ 𝐵,
𝐴 ⊂ 𝐵
• O complemento de um conjunto fuzzy 𝐴 em relação ao conjunto universo
𝑈 é indicado por 𝐴′ e a função de pertinência é definida como
𝜇𝐴′ 𝑥 = 1 − 𝜇𝐴 𝑥 , ∀ 𝑥 ∈ 𝑈

Lógica Fuzzy
• Operações
• A união de dois conjuntos fuzzy 𝐴 e 𝐵 é um conjunto fuzzy 𝐴 ∪ 𝐵 tal que
𝜇𝐴∪𝐵 𝑥 = max[𝜇𝐴 𝑥 , 𝜇𝐵(𝑥)] , ∀ 𝑥 ∈ 𝑈
• A intersecção de dois conjuntos fuzzy 𝐴 e 𝐵 é um conjunto fuzzy 𝐴 ∩ 𝐵 tal
que
𝜇𝐴∩𝐵 𝑥 = min[𝜇𝐴 𝑥 , 𝜇𝐵(𝑥)] , ∀ 𝑥 ∈ 𝑈

Lógica Fuzzy
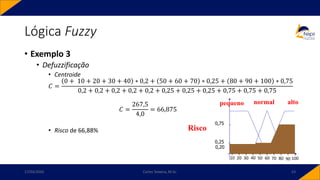
• Exemplo 2
• Consideremos 𝑈 = [0,9] e sejam 𝐴 e 𝐵 dois conjuntos fuzzy e as
respectivas funções de pertinência
𝜇𝐴: 𝑈 → [0,1] 𝜇𝐵: 𝑈 → [0,1]

Lógica Fuzzy
• Exemplo 2
• Consideremos 𝑈 = [0,9] e sejam 𝐴 e 𝐵 dois
conjuntos fuzzy e as respectivas funções de
pertinência
• Intersecção 𝐴 ∩ 𝐵
𝜇𝐴: 𝑈 → [0,1]
𝜇𝐵: 𝑈 → [0,1]

• Exemplo 2
pertinência
• União 𝐴 ∪ 𝐵
Lógica Fuzzy
𝜇𝐴: 𝑈 → [0,1]
𝜇𝐵: 𝑈 → [0,1]

• Exemplo 2
pertinência
• Complementar de 𝐵 = 𝐵′
Lógica Fuzzy
𝜇𝐴: 𝑈 → [0,1]
𝜇𝐵: 𝑈 → [0,1]

Lógica Fuzzy
• Conjunto 𝜶-Cut/𝜶-Nível
• Restrição imposta ao domínio, baseada no valor de 𝛼
• Contém todos os elementos do domínio que possuam 𝜇 𝑥 acima de uma
dado valor de 𝛼
• 𝜇 𝑥 ≥ 𝛼 → 𝛼-cut fraco
• 𝜇 𝑥 > 𝛼 → 𝛼-cut forte
• Se 𝐴 for um conjunto fuzzy, o subconjunto 𝛼-cut/𝛼-nível de 𝐴 é indicado por
𝐴 𝛼
• Útil para funções com longos “tails” que tendem a possuir valores muito
baixos de 𝜇 𝑥 por um domínio extenso
• Ajuda a retirar ruídos

Lógica Fuzzy
• Conjunto 𝜶-Cut/𝜶-Nível
• Ex.:

Lógica Fuzzy
• Funções de pertinência
• Triangular
𝜇 𝑥 =
0, 𝑥 ≤ 𝑎
𝑥 − 𝑎
𝑢 − 𝑎
, 𝑎 < 𝑥 ≤ 𝑢
𝑥 − 𝑏
𝑢 − 𝑏
, 𝑢 ≤ 𝑥 < 𝑏
0, 𝑥 ≥ 𝑏
• Trapezoidal
𝜇 𝑥 =
𝑥 − 𝑎
𝑏 − 𝑎
, 𝑎 ≤ 𝑥 < 𝑏
1, 𝑏 ≤ 𝑥 ≤ 𝑐
𝑑 − 𝑥
𝑑 − 𝑐
, 𝑐 < 𝑥 ≤ 𝑑
0, 𝑐𝑎𝑠𝑜 𝑐𝑜𝑛𝑡𝑟á𝑖𝑜

Lógica Fuzzy
• Gaussiana
𝜇 𝑥 = 𝑒
−
𝑥−𝑢 2
2𝜎2
• Sino generalizada
𝜇 𝑥 = ቐ 𝑒−
𝑥−𝑢 2
𝑎 , 𝑢 − 𝛿 ≤ 𝑥 ≤ 𝑢 + 𝛿
0, 𝑐𝑎𝑠𝑜 𝑐𝑜𝑛𝑡𝑟á𝑟𝑖𝑜

Lógica Fuzzy
• Variáveis linguísticas
• É o nome do conjunto fuzzy
• Centro da técnica de modelagem fuzzy
• Transmitem o conceito de qualificadores/modificadores (hedges)
• Hedges, por sua vez, mudam a forma do conjunto fuzzy
• Intensificadores: “muito”, “extremamente”
• Diluidores: “pouco”, “mais ou menos”
• Aproximadores: “em torno de”, “aproximadamente”, “quase”
• entre outros

Lógica Fuzzy
• Hedges
• Intensificadores: reduzem grau de pertinência dos elementos que pertencem ao
conjunto fuzzy
𝜇𝐴(𝑥) ≥ 𝜇𝑀𝑈𝐼𝑇𝑂 𝐴 𝑥
𝜇𝑀𝑈𝐼𝑇𝑂 𝐴 𝑥 = 𝜇𝐴 𝑥 2
𝜇𝐼𝑁𝑇𝐸𝑁𝑆𝐼𝐹𝐼𝐶𝐴𝐷𝑂𝑅 𝐴 𝑥 = 𝜇𝐴 𝑥 𝑛, 𝑛 > 1

Lógica Fuzzy
• Hedges
• Diluidores: diluem grau de pertinência dos elementos que pertencem ao conjunto fuzzy
𝜇𝐴 𝑥 ≤ 𝜇𝑈𝑀 𝑃𝑂𝑈𝐶𝑂 𝐴 𝑥
𝜇𝑈𝑀 𝑃𝑂𝑈𝐶𝑂 𝐴 𝑥 = 𝜇𝐴 𝑥 1/2
𝜇𝐷𝐼𝐿𝑈𝐼𝐷𝑂𝑅 𝐴 𝑥 = 𝜇𝐴 𝑥 1/𝑛
, 𝑛 > 1

Lógica Fuzzy
• Hedges
• Aproximadores: fazem o escalonamento (alargam ou estreitam) do grau de pertinência
dos elementos que pertencem ao conjunto fuzzy
𝜇𝐷𝐼𝐿𝑈𝐼𝐷𝑂𝑅 𝐴 𝑥 = 𝜇𝐴 𝑎𝑥
Se 𝑎 > 1 → compressão ou estreitamento
Se 0 < 𝑎 < 1 → expansão ou alargamento

Lógica Fuzzy
• Sistemas Fuzzy
• Fuzzificador
• Transformação das variáveis de entrada do problema em valores fuzzy. Para cada valor
de entrada é aplicada uma função de pertinência, indicando o quanto tal elemento
pertence ao conjunto
Fuzzificador
Regras
Inferência Defuzzificador
𝒙 𝒚
Modelo de Mamdani

Lógica Fuzzy
• Sistemas Fuzzy
• Regras
• Fornecidas por um especialista ou extraídas de dados numéricos, utilizando, por
exemplo, a capacidade de aprendizado de uma rede neural.
• Para elaboração dessas regras é importante conhecer: variáveis linguísticas, conexões
lógicas (E, OU, etc.) e as implicações do tipo SE/ENTÃO
Fuzzificador
Regras
𝒙 𝒚
Modelo de Mamdani

Lógica Fuzzy
• Sistemas Fuzzy
• Inferência
• Nesta etapa as regras são aplicadas aos valores já “fuzzificados”, fazendo o mapeamento
dos conjuntos fuzzy (entrada) em outros conjuntos fuzzy (saída)
• Determina como as regras são ativadas e combinadas, criando a região resultante da
aplicação das regras
Fuzzificador
Regras
𝒙 𝒚
Modelo de Mamdani

Lógica Fuzzy
• Sistemas Fuzzy
• Defuzzificação
• Corresponde à ligação funcional entre as regiões fuzzy e o valor esperado, ou seja, as
regiões resultantes do processo de inferência são convertidas em valores precisos para a
variável de saída
• Técnicas mais comuns: centroide, primeiro dos máximos, media dos máximos
Fuzzificador
Regras
𝒙 𝒚
Modelo de Mamdani

Lógica Fuzzy
• Sistemas Fuzzy
Linguístico
Numérico
Nível
Variáveis Calculadas
Variáveis Calculadas
(Valores Numéricos)
(Valores Linguísticos)
Inferência Variáveis de Comando
Defuzzificação
Planta
Fuzzificação
(Valores Linguísticos)
Variáveis de Comando
(Valores Numéricos)
Nível

Lógica Fuzzy
• Centroide: o valor de saída é o elemento do universo de discurso
correspondente ao centro de gravidade da função pertinência de saída
z0

Lógica Fuzzy
• Primeiro dos Máximos: é o elemento do universo de discurso correspondente
ao primeiro ponto entre os valores que tem o maior grau de pertinência
inferido pelas regras
z0

Lógica Fuzzy
• Média dos Máximos: é o elemento do universo de discurso correspondente
ao valor médio entre os valores que tem o maior grau de pertinência inferido
pelas regras
z0

• Exemplo 3
• Objetivo do sistema
• Determinar o risco de um projeto
• Entrada
• Quantidade de dinheiro
• Pessoas envolvidas
• Base de conhecimento (regras)
1. Se dinheiro é adequado OU pessoal é baixo ENTÃO risco é pequeno
2. Se dinheiro é médio E pessoal é alto ENTÃO risco é normal
3. Se dinheiro é inadequado ENTÃO risco é alto
• Problema a ser resolvido
• Dinheiro = 35%
• Pessoal = 60%
Lógica Fuzzy

• Exemplo 3
• Fuzzificação
Lógica Fuzzy
Dinheiro
Inadequado
Médio
Adequado
35
.25
.75
Baixo Alto
Pessoal
60
.2
.8
𝝁𝒊 𝟑𝟓 = 𝟎, 𝟕𝟓
𝝁𝒎 𝟑𝟓 = 𝟎, 𝟐𝟓
𝝁𝒂 𝟑𝟓 = 𝟎
𝝁𝒃 𝟔𝟎 = 𝟎, 𝟐
𝝁𝒂 𝟔𝟎 = 𝟎, 𝟖

• Exemplo 3
• Regras
• OU → Máximo
Lógica Fuzzy
Adequado Baixo
0,0
ou
0,2
Risco

• Exemplo 3
• Regras
• E → Mínimo
Lógica Fuzzy
médio Alto
0,25
e
0,8
Risco

• Exemplo 3
• Regras
Lógica Fuzzy
Risco
Inadequado
0,75

• Exemplo 3
• Centroide
𝐶 =
0 + 10 + 20 + 30 + 40 ∗ 0,2 + 50 + 60 + 70 ∗ 0,25 + 80 + 90 + 100 ∗ 0,75
0,2 + 0,2 + 0,2 + 0,2 + 0,2 + 0,25 + 0,25 + 0,25 + 0,75 + 0,75 + 0,75
𝐶 =
267,5
4,0
= 66,875
• Risco de 66,88%
Lógica Fuzzy
Risco
0,75
0,25
pequeno normal alto
0,20
10 20 30 40 70
60
50 100
90
80

Software
Passo-a-passo

• Software InFuzzy
Lógica Fuzzy

• Criação de projeto
Lógica Fuzzy
Duplo-clique
Clique no ícone para salvar
alterações

• Definições do projeto
• AND
• Mínimo (Norma-T)
• Produto Algébrico (Norma-T)
• Produto Limitado (Norma T)
Lógica Fuzzy

• OR
• Máximo (Conorma-T)
• Soma Algébrica (Conorma-T)
• Soma Limitada (Conorma T)
Lógica Fuzzy

• Implicação
• Mínimo (Norma-T)
Lógica Fuzzy

• Agregação
• Máximo (Conorma-T)
• Soma Algébrica (Conorma-T)
• Soma Limitada (Conorma T)
Lógica Fuzzy

• Defuzificação
• Centro de Gravidade
• Primeiro dos Máximos
• Centro dos Máximos
• Último dos Máximos
• Média dos Máximos
• Altura
Lógica Fuzzy

• Passos (usado em alguns métodos de defuzificação
• 0,01
• 0,10
• 0,50
• 1,00
• 2,00
• 5,00
• 10,0
Lógica Fuzzy

• Organização do Projeto
• Variáveis de Entrada
• Variáveis de Saída
• Bloco de Regras
• Texto
Lógica Fuzzy

• Área de Trabalho
• Acesso às propriedades e seleção de objetos
• Adicionar variáveis de entrada
• Adicionar variáveis de saída
• Adicionar blocos de regras
• Realizar conexões entre blocos de regras e variáveis
• Adicionar texto
• Excluir objetos
• Movimentar objetos
• Configurar preferências do projeto
• Ferramenta de simulação
Lógica Fuzzy

• Área de Trabalho
Lógica Fuzzy

• Entrada
• Incluir
• Função
• Termo linguístico
• Cor
• Valores das variáveis relacionadas à função
Lógica Fuzzy

• Entrada
Lógica Fuzzy

• Entrada
• Incluir
• Função
• Cor
Lógica Fuzzy

• Entrada
Lógica Fuzzy

• Saída
• Incluir
• Função
• Cor
Lógica Fuzzy

• Saída
Lógica Fuzzy

• Bloco de Regras
Lógica Fuzzy

• Salvar projeto
Lógica Fuzzy

• Simulação
• Tabela de Simulação
• Descrição das Etapas de Simulação
• Descritivo do Sistema Fuzzy
• Gráfico de Defuzificação
• Histórico de Saídas
• Debug de Comunicação
Lógica Fuzzy

• Simulação
• Tabela de Simulação
• Simulação Manual
• Selecionar simulação
• Executar
Lógica Fuzzy

• Simulação
• Gráfico de Defuzificação
Lógica Fuzzy

Controles Fuzzy
Teoria

• Introdução
• Controle PID (Clássico)
• Expressão geral
𝑢 𝑡 = 𝐾𝑝𝑒 𝑡 + 𝐾𝑖 න
0
𝑡
𝑒 𝑡 𝑑𝑡 + 𝐾𝑑
𝑑𝑒 𝑡
𝑑𝑡
Para uma melhor associação com os polos e zeros da F.T.:
𝑢 𝑡 = 𝐾𝑝 𝑒 𝑡 +
1
𝑇𝑖
න
0
𝑡
𝑒 𝜏 𝑑𝜏 + 𝑇𝑑
𝑑𝑒 𝑡
𝑑𝑡
em que, 𝑇𝑖 e 𝑇𝑑 são os tempos integral e derivativo, respectivamente, tais que 𝐾𝑖 = 𝐾𝑝/𝑇𝑖
e 𝐾𝑑 = 𝐾𝑝𝑇𝑑
• Função de transferência
𝑈 𝑠
𝐸(𝑠)
= 𝐶(𝑠) = 𝐾𝑝 1 +
1
𝑠𝑇𝑖
+ 𝑠𝑇𝑑
Controles Fuzzy

• Introdução
• Expressão geral na forma discreta (simplificada)
𝑢 𝑘 = 𝐾𝑝 𝑒 𝑘 +
𝑇
𝑇𝑖
෍
𝑘=0
𝑛
𝑒 𝑘 +
𝑇𝑑
𝑇
𝑒 𝑘 − 𝑒 𝑘 − 1
Controles Fuzzy

• Introdução
• Ação proporcional
• Reduz o tempo de subida/descida
• Não elimina o erro em regime permanente
• Ação integral
• Elimina erro em regime permanente
• Piora a resposta transitória
• Controle puramente integral: sistema sempre instável (polo na origem)
• Ação derivativa
• Aumenta a estabilidade do sistema
• Melhora a resposta transitória
• Controle puramente derivativo: ação de controle zerada quando o erro for constante
Controles Fuzzy

• Introdução
• Sintonização dos coeficientes
• Métodos clássicos
• Regras de Ziegler-Nichols
• Ajuste empírico
• Apoiado nos métodos root-locus ou resposta em frequência
• Necessitam do modelo da planta
Controles Fuzzy

• Introdução
• Sintonização dos coeficientes
• Métodos clássicos
• Se o sistema for levemente não-linear, ajustes periódicos dos parâmetros são necessários
• Se o sistema for altamente não-linear, os controles PID convencionais têm baixo
desempenho
Controles Fuzzy

• Introdução
• Controles Fuzzy baseado em regras
• Funções lineares e não-lineares podem ser implementadas por um sistema baseado em
regras, usando o conhecimento de um especialista formulado em termos linguísticos
• Capaz de completar determinada tarefa de processamento sem envolver muitos cálculos
• São robustos e resistentes a distúrbios externos
Controles Fuzzy

• Introdução
• Controles Fuzzy baseado em regras
• Esquema
Controles Fuzzy

• Introdução
• Controles PID-Fuzzy
• As regras que definem o modelo estão diretamente associadas ao controle PID discreto
(clássico)
• Expressa linguisticamente as relações entre o erro, a variação do erro - às vezes, a
variação da variação do erro - e a correspondente ação de controle
• Opções de construção
• Controlador P-Fuzzy
• Controlador PI-Fuzzy
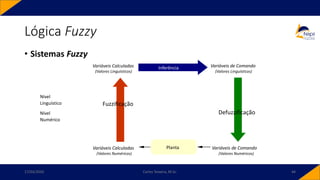
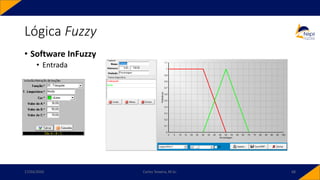
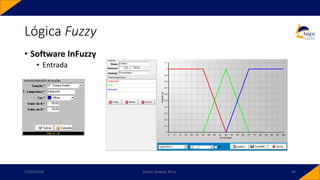
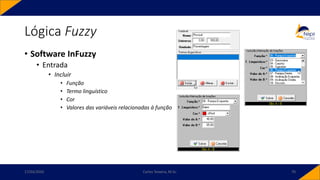
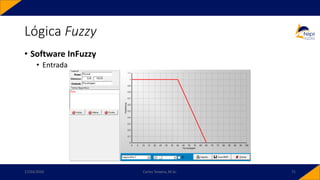
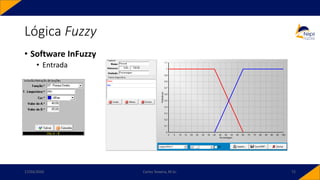
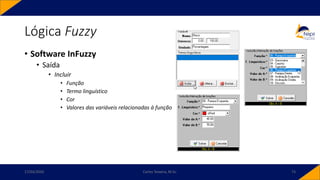
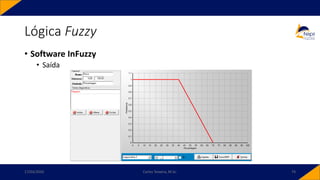
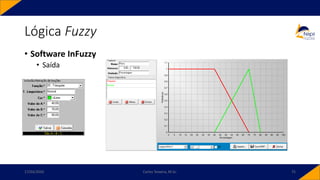
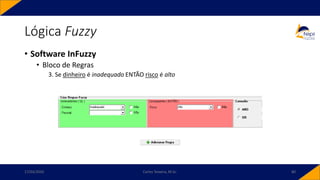
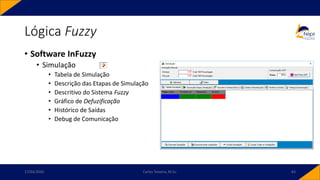
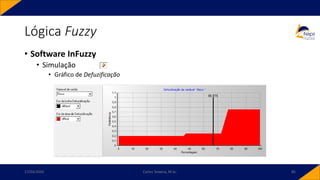
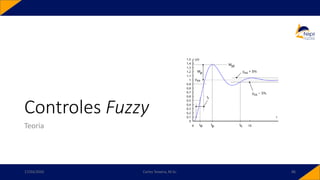
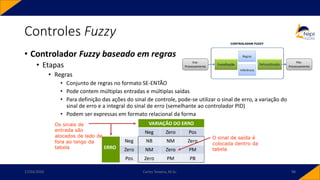
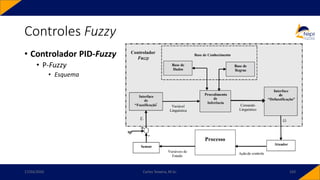
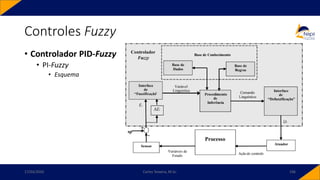
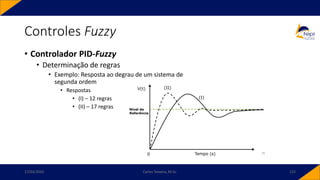
• Controlador PID-Fuzzy
Controles Fuzzy

• Controlador Fuzzy baseado em regras
Controles Fuzzy

• Etapas
• Pré-processamento
• Recebe as medições realizadas pela aquisição de dados
• Realiza o condicionamento dos dados
• Ganho/atenuação
• Normalização
• Filtragem
• LUT (Look-up-table)
Controles Fuzzy

• Etapas
• Fuzzyficação
• Definição das funções de pertinência
• Nome dos conjuntos (variáveis linguísticas) e modificadores (hedges)
• Ex. 1: Zero, Pos, Neg
• Ex. 2: NB, NM, NS, Z, PS, PM, PB (negativo grande, negativo médio, negativo pequeno,
zero, positivo pequeno, positivo médio, positivo grande)
• Realiza a avaliação das entradas de acordo com as regras
• Retorna como resultado o grau de pertinência da regra
Controles Fuzzy

• Etapas
• Regras
• Conjunto de regras no formato SE-ENTÃO
• Pode contem múltiplas entradas e múltiplas saídas
• Para definição das ações do sinal de controle, pode-se utilizar o sinal de erro, a variação do
sinal de erro e a integral do sinal de erro (semelhante ao controlador PID)
• Podem ser expressas em formato relacional da forma
Controles Fuzzy

• Etapas
• Inferência
• Realiza o mapeamento dos conjuntos fuzzy (entrada) em outros conjuntos fuzzy (saída)
• Determina como as regras são combinadas, criando a região resultante da aplicação das
regras
Controles Fuzzy

• Etapas
• Defuzzyficação
• Converte as regiões resultantes do processo de inferência em valores para a variável de saída
• Variável linguística → variável numérica
• Técnicas mais comuns: centroide, primeiro dos máximos, media dos máximos
Controles Fuzzy
z0
z0
z0

• Etapas
• Pós-processamento
• Como normalmente o universo de discurso é dado em porcentagem ou normalizado, esta
etapa pode realizar o escalonamento
• Esta etapa pode também realizar ganho ou atenuação
Controles Fuzzy

• P-Fuzzy
• Para uma entrada e uma saída
𝑈(𝑘) = 𝐾𝑝𝐸(𝑘)
em que, 𝐸 é o erro entre o sinal de referência e a variável do processo.
• Regra de controle fuzzy
𝑆𝐸 𝑒𝑟𝑟𝑜 = 𝐸𝑖 𝐸𝑁𝑇Ã𝑂 𝑐𝑜𝑛𝑡𝑟𝑜𝑙𝑒 = 𝑈𝑖
em que, 𝐸𝑖 e 𝑈𝑖 são funções de pertinência linguísticas atribuídas às variáveis 𝑒 e 𝑢.
Controles Fuzzy

• P-Fuzzy
• Esquema
Controles Fuzzy

• PI-Fuzzy
• Possui como entradas o sinal de erro e o sinal de variação do erro. Para o instante 𝑘,
𝑈 𝑘 = 𝐾𝑝𝐸 𝑘 + 𝐾𝑝
𝑇
𝑇𝑖
෍
𝑛=0
𝑘
𝐸(𝑛)
Para o instante 𝑘 − 1
𝑈 𝑘 − 1 = 𝐾𝑝𝐸 𝑘 − 1 + 𝐾𝑝
𝑇
𝑇𝑖
෍
𝑛=0
𝑘−1
𝐸(𝑛)
Portanto, a variação da ação de controle é dada por
𝑈 𝑘 − 𝑈 𝑘 − 1 = 𝐾𝑝 𝐸 𝑘 − 𝐸 𝑘 − 1 + 𝐾𝑝
𝑇
𝑇𝑖
𝐸(𝑘)
Controles Fuzzy

• PI-Fuzzy
Logo, a saída será a variação da ação de controle
Δ𝑈 𝑘 = KpΔE k + 𝐾𝑝
𝑇
𝑇𝑖
𝐸(𝑘)
𝑆𝐸 𝑒𝑟𝑟𝑜 = 𝐸𝑖 𝐸 (𝑣𝑎𝑟𝑖𝑎çã𝑜 𝑑𝑜 𝑒𝑟𝑟𝑜 = Δ𝐸𝑖) 𝐸𝑁𝑇Ã𝑂 𝑣𝑎𝑟𝑖𝑎çã𝑜 𝑑𝑎 𝑎çã𝑜 𝑑𝑒 𝑐𝑜𝑛𝑡𝑟𝑜𝑙𝑒 = Δ𝑈𝑖
Controles Fuzzy

• PI-Fuzzy
• Esquema
Controles Fuzzy

• PID-Fuzzy
• Possui como entradas o sinal de erro, o sinal de variação do erro e o sinal da variação da
variação do erro. Para o instante 𝑘,
𝑈 𝑘 = 𝐾𝑝𝐸 𝑘 + 𝐾𝑝
𝑇
𝑇𝑖
෍
𝑛=0
𝑘
𝐸(𝑛) + 𝐾𝑝
𝑇𝑑
𝑇
[𝐸 𝑘 − 𝐸(𝑘 − 1)]
Para o instante 𝑘 − 1
𝑈 𝑘 − 1 = 𝐾𝑝𝐸 𝑘 − 1 + 𝐾𝑝
𝑇
𝑇𝑖
෍
𝑛=0
𝑘−1
𝐸(𝑛) + 𝐾𝑝
𝑇𝑑
𝑇
[𝐸 𝑘 − 1 − 𝐸(𝑘 − 2)]
Portanto, a variação da ação de controle é dada por
𝑈 𝑘 − 𝑈 𝑘 − 1 = 𝐾𝑝 𝐸 𝑘 − 𝐸 𝑘 − 1 + 𝐾𝑝
𝑇
𝑇𝑖
𝐸 𝑘 + 𝐾𝑝
𝑇𝑑
𝑇
Δ𝐸 𝑘 − Δ𝐸 𝑘 − 1
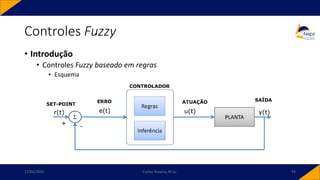
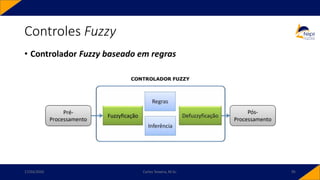
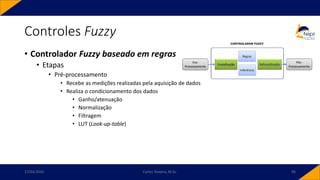
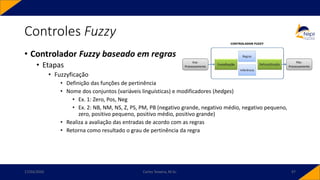
Controles Fuzzy

• PID-Fuzzy
Logo, a saída será a variação da ação de controle
Δ𝑈 𝑘 = KpΔE k + 𝐾𝑝
𝑇
𝑇𝑖
𝐸 𝑘 + 𝐾𝑝
𝑇𝑑
𝑇
Δ2𝐸(𝑘)
𝑆𝐸 𝑒𝑟𝑟𝑜 = 𝐸𝑖 𝐸 𝑣𝑎𝑟𝑖𝑎çã𝑜 𝑑𝑜 𝑒𝑟𝑟𝑜 = Δ𝐸𝑖 𝐸 𝑣𝑎𝑟𝑖𝑎çã𝑜 𝑑𝑎 𝑣𝑎𝑟𝑖𝑎çã𝑜 𝑑𝑜 𝑒𝑟𝑟𝑜 = Δ2𝐸𝑖
𝐸𝑁𝑇Ã𝑂 𝑣𝑎𝑟𝑖𝑎çã𝑜 𝑑𝑎 𝑎çã𝑜 𝑑𝑒 𝑐𝑜𝑛𝑡𝑟𝑜𝑙𝑒 = Δ𝑈𝑖
Controles Fuzzy

• Determinação de regras
• A resposta de controladores convencionais é frequentemente especificada em termos do
comportamento do sistema em malha-fechada e de desempenho transitório
• Erro em regime permanente
• Máximo pico
• Tempo de acomodação
• As regras de controle fuzzy podem também ser especificadas por intermédio de um
comportamento desejado em regime permanente e de uma resposta transitória expressas
em termos linguísticos
• Tempo de subida rápido
• Erro em regime permanente aproximadamente nulo
Controles Fuzzy

• Exemplo: Resposta ao degrau de um sistema de segunda ordem
• Necessidades:
• Tempo de subida (𝑡𝑟) rápido
• Máximo pico mínimo
• Entradas
• Erro 𝐸
• Variação de erro Δ𝐸
• Saída
• Variação do sinal de controle Δ𝑈
Controles Fuzzy

• Erro
𝑒𝑟𝑟𝑜 = 𝑟𝑒𝑓𝑒𝑟ê𝑛𝑐𝑖𝑎 − 𝑠𝑎í𝑑𝑎
Um valor negativo de erro indica que
𝑦 𝑡 > 𝑦𝑆𝑆
Um valor positivo de erro indica que
𝑦 𝑡 < 𝑦𝑆𝑆
Controles Fuzzy

• Variação do erro
Δ𝑒𝑟𝑟𝑜 = 𝑟𝑒𝑓 − 𝑠𝑎í𝑑𝑎𝑎𝑡𝑢𝑎𝑙 − 𝑟𝑒𝑓 − 𝑠𝑎í𝑑𝑎𝑎𝑛𝑡𝑒𝑟𝑖𝑜𝑟
Δ𝑒𝑟𝑟𝑜 = −(𝑠𝑎í𝑑𝑎𝑎𝑡𝑢𝑎𝑙 − 𝑠𝑎í𝑑𝑎𝑎𝑛𝑡𝑒𝑟𝑖𝑜𝑟)
Um valor negativo de variação de erro indica que
𝑦 𝑡 está crescendo
Um valor positivo de variação de erro indica que
𝑦 𝑡 está diminuindo
Controles Fuzzy

• Exemplo: Resposta ao degrau de um sistema de
segunda ordem
• As regras são obtidas considerando os pontos de
cruzamento de máximo e de mínimo da resposta do
sistema em malha aberta
• As ações de controle são sugeridas em cada ponto
para gerar um resposta em malha fechada com um
tempo de subida rápido e com um mínimo máximo-
pico
Controles Fuzzy

segunda ordem
• Entradas: Erro e variação de erro
• Saída: Variação do sinal de controle
Controles Fuzzy

segunda ordem
Controles Fuzzy

segunda ordem
• Mapa de regras – Regra 1
𝑆𝑒 (𝐸 = 𝑃𝐵) 𝐸 (Δ𝐸 = 𝑍) 𝐸𝑁𝑇Ã𝑂 (𝑈 = 𝑃𝐵)
𝑒𝑟𝑟𝑜(0) = 𝑟𝑒𝑓 − 𝑉 0 → 𝐸 = 𝑃𝐵
Δ𝑒𝑟𝑟𝑜(0) = 𝑒𝑟𝑟𝑜 0 − 𝑒𝑟𝑟𝑜 −1
𝑒𝑟𝑟𝑜 0 ≅ 𝑒𝑟𝑟𝑜 −1 → Δ𝐸 = 0
Controles Fuzzy
partida → Grande aceleração negativa

segunda ordem
𝑆𝑒 (𝐸 = 𝑍) 𝐸 (Δ𝐸 = 𝑃𝐵) 𝐸𝑁𝑇Ã𝑂 (𝑈 = 𝑁𝐵)
Controles Fuzzy
Grande acelaração positiva → freio

segunda ordem
𝑆𝑒 (𝐸 = 𝑁𝐵) 𝐸 (Δ𝐸 = 𝑍) 𝐸𝑁𝑇Ã𝑂 (𝑈 = 𝑁𝐵)
Controles Fuzzy
Freio → Grande aceleração negativa

segunda ordem
𝑆𝑒 (𝐸 = 𝑍) 𝐸 (Δ𝐸 = 𝑁𝐵) 𝐸𝑁𝑇Ã𝑂 (𝑈 = 𝑃𝐵)
Controles Fuzzy
Grande aceleração negativa → freio

segunda ordem
• Mapa de regras – Tabela (12 regras)
Controles Fuzzy

segunda ordem
• Mapa de regras – Tabela (17 regras)
Controles Fuzzy

segunda ordem
• Respostas
• (I) – 12 regras
• (II) – 17 regras
Controles Fuzzy

2020 - Inteligência Artificial fuzzy.pdf

Mais conteúdo relacionado

Destaque

2020 - Inteligência Artificial fuzzy.pdf