Este documento apresenta um resumo sobre matrizes em três frases: - Uma matriz é uma estrutura de dados homogênea de duas ou mais dimensões que utiliza variáveis indexadas por mais de um índice. - Os elementos de uma matriz podem ser acessados e atribuídos valores utilizando seus índices de linha e coluna. - Exemplos resolvidos demonstram como ler e imprimir elementos específicos de uma matriz 3x3 de acordo com diferentes condições.

1. Disciplina: Constr. de Algoritmos e Prog. de Sistemas
Professor: Jeovane Reges
Caxias – MA
2016
ACULDADE DE CIÊNCIAS
E TECNOLOGIA DO
MARANHÃO

2. Link Drive
bit.ly/ads-algoritmos
2

3. 3
Algoritmos

4. 4
Estruturas Homogêneas
<Matrizes>

5. • Algoritmos
• Estruturas Homogêneas
• Matrizes
• Os tipos de dados simples nem sempre são
suficientes para resolver certos problemas.
• Alguns problemas necessitam de estruturas que
comportem-se como uma "lista" (vetores).
• Porém, os vetores são unidimensionais, e alguns
problemas são resolvidos apenas com estruturas
multidimensionais.
5

6. 6
Uma matriz é uma estrutura de dados
homogênea de duas (ou mais)
dimensões. Uma matriz utiliza variáveis
indexadas de mais de um índice.

7. • Algoritmos
• Estruturas Homogêneas
• Matrizes
 Matriz 3 x 3
7
M =
Linhas
Colunas

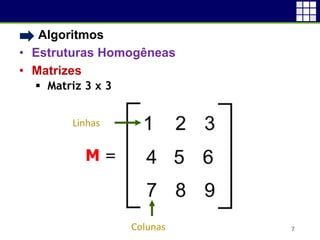
8. • Algoritmos
• Estruturas Homogêneas
• Matrizes
 Matriz 3 x 3
8
Matriz M Coluna 1 Coluna 2 Coluna 3
Linha 1 M[1,1] M[1,2] M[1,3]
Linha 2 M[2,1] M[2,2] M[2,3]
Linha 3 M[3,1] M[3,2] M[3,3]
Nome da
Matriz
Índice da linha Índice da coluna

9. • Algoritmos
• Estruturas Homogêneas
• Matrizes
9
M[?,?]=?
Linha (i)
Coluna (j)

10. • Algoritmos
• Estruturas Homogêneas
• Matrizes
 Acessando os valores da matriz 3 x 3:
10
M[1,1] = 1
M[1,2] = ?
M[1,3] = ?
M[2,1] = ?
M[2,2] = ?
M[2,3] = ?
M[3,1] = ?
M[3,2] = ?
M[3,3] = ?
M =
1 2 3
1
2
3

11. • Algoritmos
• Estruturas Homogêneas
• Matrizes
 Acessando os valores da matriz 3 x 3:
11
M[1,1] = 1
M[1,2] = 2
M[1,3] = 3
M[2,1] = 4
M[2,2] = 5
M[2,3] = 6
M[3,1] = 7
M[3,2] = 8
M[3,3] = 9
M =
1 2 3
1
2
3

12. • Algoritmos
• Estruturas Homogêneas
• Matrizes
 Sintaxe:
• Tam1 e Tam2 <tamanho> = [Vi..Vf],
 Vi = valor inicial; e
 Vf = valor final.
12
<identificador>: vetor [tam1, tam2] de <tipo>

13. • Algoritmos
• Estruturas Homogêneas
• Matrizes
 Exemplo:
// 1..3 = 3 linhas
// 1..2 = 2 colunas
13
nomes : vetor [1..3, 1..2] de literal
Números de colunas
Números de linhas

14. 14
Matrizes
(Atribuição de valores)

15. • Algoritmos
• Estruturas Homogêneas
• Matrizes → Atribuição de valores
• Assim como com os vetores, os elementos de
uma matriz também podem ser inicializados.
• Sintaxe:
15
<identificador>[pos1, pos2] ← <valor>
Linha
Coluna

16. • Algoritmos
• Estruturas Homogêneas
• Matrizes → Atribuição de valores
 Exemplo: {1}
16
algoritmo "ExMatrizes"
var
nomes: vetor [1..2, 1..2] de literal
inicio
nomes[1,1] ← "Pedro"
nomes[1,2] ← "João"
nomes[2,1] ← "Maria"
nomes[2,2] ← "Francisca"
fimalgoritmo

17. • Algoritmos
• Estruturas Homogêneas
• Matrizes → Atribuição de valores
 Exemplo: {1}
 // nomes[1,1] ← "Pedro"
 // nomes[1,2] ← "João"
 // nomes[2,1] ← "Maria"
 // nomes[2,2] ← "Francisca"
17
1
2
1 2
Pedro João
Maria Francisca

18. • Algoritmos
• Estruturas Homogêneas
18
para i de 1 ate 2 faca
para j de 1 ate 2 faca
1. Indica a partir de qual linha será iniciado o acesso.
2. Indica até qual linha será acessada.
3. Indica a partir de qual coluna será iniciado o acesso.
4. Indica até que coluna será acessada.
21
43

19. • Algoritmos
• Estruturas Homogêneas
• Matrizes → Atribuição de valores
 Exemplo: {2}
19
algoritmo "ExMatrizes"
var
nomes: vetor [1..2, 1..2] de literal
i, j: inteiro
inicio
para i de 1 ate 2 faca
para j de 1 ate 2 faca
escreva("Digite um nome: ")
leia(nomes[i,j])
fimpara
fimpara
fimalgoritmo
Linhas
Colunas

20. 20
Matrizes
(Acessando valores)

21. • Algoritmos
• Estruturas Homogêneas
 Matriz 3 x 3
21
M =
// Para resolver os próximos problemas parta do principio que essa
matriz está preenchida.

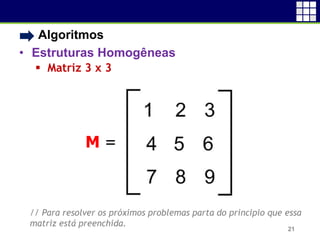
22. • Algoritmos
• Estruturas Homogêneas
 Exemplo: {1}
22
algoritmo "ExMatrizes"
var
M: vetor [1..3, 1..3] de inteiro
inicio
escreval("M{1,1}: ", M[1,1])
escreval("M{1,2}: ", M[1,2])
escreval("M{1,3}: ", M[1,3])
escreval("M{2,1}: ", M[2,1])
escreval("M{2,2}: ", M[2,2])
escreval("M{2,3}: ", M[2,3])
escreval("M{3,1}: ", M[3,1])
escreval("M{3,2}: ", M[3,2])
escreval("M{3,3}: ", M[3,3])
fimalgoritmo

23. • Algoritmos
• Estruturas Homogêneas
 Exemplo: {2}
23
algoritmo "ExMatrizes"
var
M: vetor [1..3, 1..3] de inteiro
i, j: inteiro
inicio
para i de 1 ate 3 faca
para j de 1 ate 3 faca
escreva(M[i,j])
fimpara
escreval()
fimpara
fimalgoritmo

24. 24
Exemplos Resolvidos
<Matrizes>

25. Faça um algoritmo que leia os elementos de uma
"matriz inteira 3 x 3" e imprima os elementos da
diagonal principal e abaixo.
25
Problema I

26. 26
M =
1 2 3
1
2
3
M[1,1] = 1
M[2,1] = 4
M[2,2] = 5
M[3,1] = 7
M[3,2] = 8
M[3,3] = 9
Problema IAnalisando o

27. • Algoritmos
• Estruturas Homogêneas
 Problema I
27
algoritmo "Problema 01"
var
M: vetor [1..3, 1..3] de inteiro
i, j: inteiro
inicio
para i de 1 ate 3 faca
para j de 1 ate i faca
escreva(M[i,j])
fimpara
escreval()
fimpara
fimalgoritmo

28. Problema I
Faça um algoritmo que leia os elementos de uma
"matriz inteira 3 x 3" e imprima os elementos
abaixo da diagonal principal.
28
Problema II

29. 29
M =
1 2 3
1
2
3
M[2,1] = 4
M[3,1] = 7
M[3,2] = 8
Problema IIAnalisando o

30. • Algoritmos
• Estruturas Homogêneas
 Problema II
30
algoritmo "Problema 02"
var
M: vetor [1..3, 1..3] de inteiro
i, j: inteiro
inicio
para i de 2 ate 3 faca
para j de 1 ate (i – 1) faca
escreva(M[i,j])
fimpara
escreval()
fimpara
fimalgoritmo

31. Problema I
Faça um algoritmo que leia os elementos de uma
"matriz inteira 3 x 3" e imprima os elementos da
diagonal principal e acima.
31
Problema III

32. 32
M =
M[1,1] = 1
M[1,2] = 2
M[1,3] = 3
M[2,2] = 5
M[2,3] = 6
M[3,3] = 9
1 2 3
1
2
3
Problema IIIAnalisando o

33. • Algoritmos
• Estruturas Homogêneas
 Problema III
33
algoritmo "Problema 03"
var
M: vetor [1..3, 1..3] de inteiro
i, j: inteiro
inicio
para i de 2 ate 3 faca
para j de i ate 3 faca
escreva(M[i,j])
fimpara
escreval()
fimpara
fimalgoritmo

34. Problema I
Criar um algoritmo que leia os elementos de uma
"matriz inteira 3 x 3" e imprima os elementos
acima da diagonal principal.
34
Problema IV

35. 35
M =
M[1,2] = 2
M[1,3] = 3
M[2,3] = 6
1 2 3
1
2
3
Problema IVAnalisando o

36. • Algoritmos
• Estruturas Homogêneas
 Problema IV
36
algoritmo "Problema 04"
var
M: vetor [1..3, 1..3] de inteiro
i, j: inteiro
inicio
para i de 1 ate 2 faca
para j de (i + 1) ate 3 faca
escreva(M[i,j])
fimpara
escreval()
fimpara
fimalgoritmo

37. I
Faça um algoritmo que leia os elementos de uma
"matriz inteira 3 x 3" e imprima os elementos da
diagonal principal.
37
Problema V

38. 38
Problema VAnalisando o
M =
1 2 3
1
2
3
M[1,1] = 1
M[2,2] = 5
M[3,3] = 9

39. • Algoritmos
• Estruturas Homogêneas
 Problema V
39
algoritmo "Problema 05"
var
M: vetor [1..3, 1..3] de inteiro
i, j: inteiro
inicio
para i de 1 ate 3 faca
para j de i ate i faca
escreva(M[i,j])
fimpara
escreval()
fimpara
fimalgoritmo