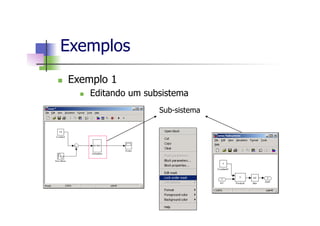
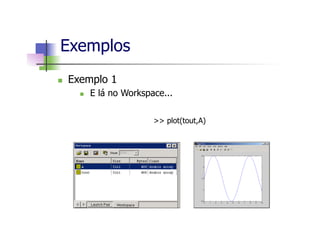
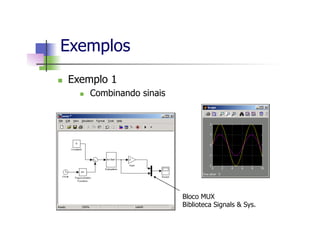
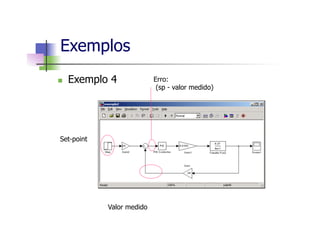
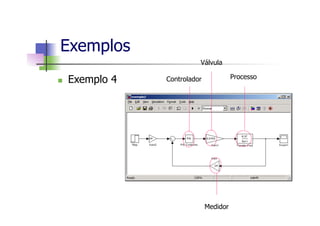
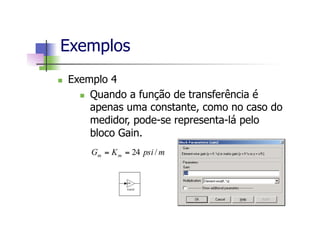
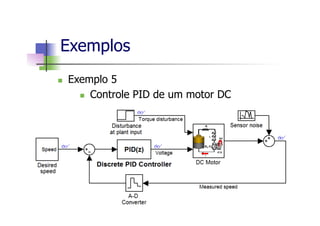
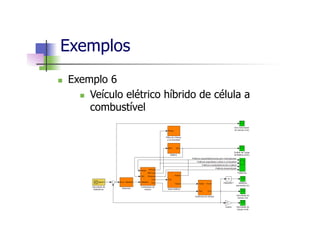
Este documento apresenta um mini-curso de MATLAB com os seguintes tópicos: 1) Introdução ao MATLAB, 2) Matlab Básico, 3) Programação em Matlab, 4) Matemática Simbólica, 5) Interfaces gráficas e Toolbox, 6) Simulink. O documento inclui referências bibliográficas e informações sobre os professores.
















![Variáveis e funções
n Criando e iniciando variáveis:
n Expressões de atribuição
n Entrada pelo Teclado
19
var = 40i;
var2 = var/5;
x = 1; y = 2;
array = [1 2 3 4];
my_val = input('Enter an input value:');](https://image.slidesharecdn.com/minicursomatlabivsee2013semvideo-130627183525-phpapp01/85/Minicurso-Matlab-IVSEE-2013-UERJ-19-320.jpg)
![Variáveis e funções
n Criando e iniciando variáveis:
n Expressões de atalho
n Funções pré-definidas
20
x = 1:2:10
angles = (0.01:0.01:1.00)*pi;
a = zeros(2);
b = zeros(2,3);
c = [1 2; 3 4];
d = zeros(size(c));](https://image.slidesharecdn.com/minicursomatlabivsee2013semvideo-130627183525-phpapp01/85/Minicurso-Matlab-IVSEE-2013-UERJ-20-320.jpg)










![Variáveis e funções
n função disp(str)
n >> str = ['The value of pi = ' num2str(pi)];
n >> disp (str);
n função fprintf(format,data)
n >> fprintf('The value of pi is %f n',pi)
n >> fprintf('The value of pi is %6.2f n',pi)
31
Formatação Resultados
%d Exibe valor como inteiro
%e Exibe valor no formato científico
%f Exibe valor como ponto flutuante
n Muda de linha](https://image.slidesharecdn.com/minicursomatlabivsee2013semvideo-130627183525-phpapp01/85/Minicurso-Matlab-IVSEE-2013-UERJ-31-320.jpg)

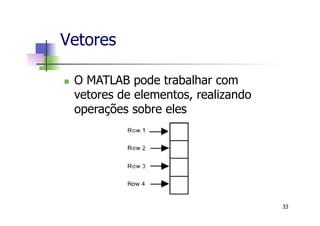
![Vetores
n Definição de vetores
n >> A = [0 1 2 3 4 5]
A =
0 1 2 3 4 5
n Outra forma de se criar um conjunto:
n >> A = 1:1:5
A =
1 2 3 4 5
n O primeiro valor é o valor inicial, o segundo o
“salto”e o terceiro o valor final.
34](https://image.slidesharecdn.com/minicursomatlabivsee2013semvideo-130627183525-phpapp01/85/Minicurso-Matlab-IVSEE-2013-UERJ-34-320.jpg)




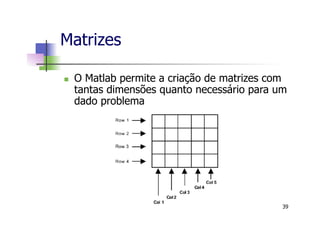
![Matrizes
n Definição de matrizes:
n >> M = [1 0 -1; 2 3 4; -7 1 3]
M =
1 0 -1
2 3 4
-7 1 3
n Os elementos da linha são separados por
espaço em branco e as linhas são
separadas por ponto-e-vírgula.
40](https://image.slidesharecdn.com/minicursomatlabivsee2013semvideo-130627183525-phpapp01/85/Minicurso-Matlab-IVSEE-2013-UERJ-40-320.jpg)
![Matrizes
n Pode-se criar matrizes a partir de
vetores ou outras matrizes
n >> b = [2 -3 1];
n >> Mx = [b' M(:,2:3)]
Mx =
2 0 -1
-3 3 4
1 1 3
41](https://image.slidesharecdn.com/minicursomatlabivsee2013semvideo-130627183525-phpapp01/85/Minicurso-Matlab-IVSEE-2013-UERJ-41-320.jpg)











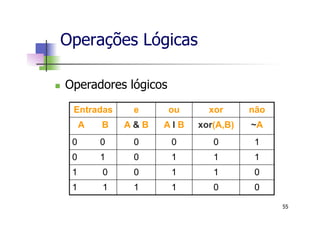
![n Operadores relacionais
Expressão Resultado
5 > 3 1
‘AC’ > ‘BA´ 0 1
a > b 1 0
1 + j <= 2 + 3*j 1
x >= [3 8] 1 0
a > c 0 1
2 + j == 1+ j 0
5 + j ~= 2 + j 1
a = [2 1] b = [ 1 1 ] c = [ 0 2 ] x = [ 4 2]
Operações Relacionais
53](https://image.slidesharecdn.com/minicursomatlabivsee2013semvideo-130627183525-phpapp01/85/Minicurso-Matlab-IVSEE-2013-UERJ-53-320.jpg)




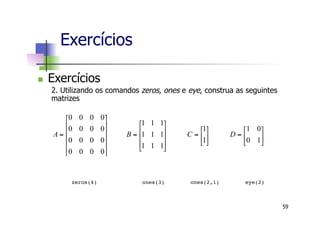



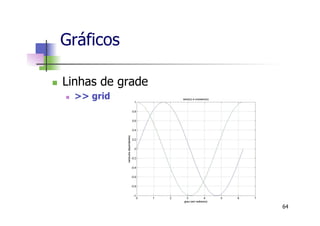

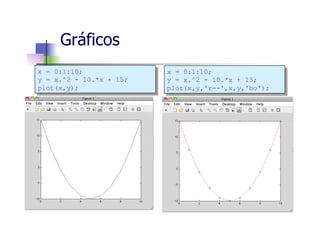



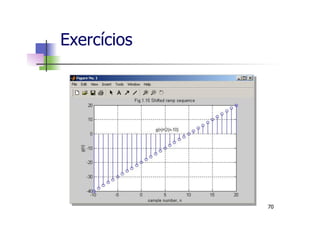
![n Sequência exponencial Real
n Definida como:
n Exemplo para A = 10 e a = 0.9, a sequência
aproxima-se de zero quando n tende para infinito e
aproxima-se de mais infinito quando n tende para
menos infinito
Exercícios
n
aAnf )()( =
Código MATLAB:
n=-10:1:10;
f =10*(.9).^n;
stem(n,f);
axis([-10 10 0 30]); 71](https://image.slidesharecdn.com/minicursomatlabivsee2013semvideo-130627183525-phpapp01/85/Minicurso-Matlab-IVSEE-2013-UERJ-71-320.jpg)
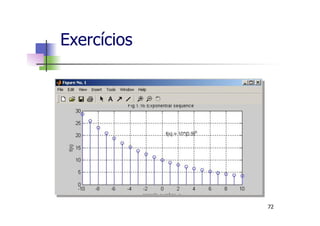

![n Sequência senoidal
Exercícios
Código MATLAB:
1. n=-20:1:20;
2. f=5*[cos(n*pi/8+pi/4)];
3. stem(n,f);
74](https://image.slidesharecdn.com/minicursomatlabivsee2013semvideo-130627183525-phpapp01/85/Minicurso-Matlab-IVSEE-2013-UERJ-74-320.jpg)
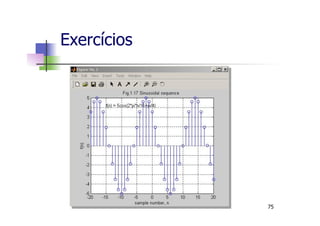

![n Sequência senoidal modulada
exponencialmente
Exercícios
Código MATLAB:
1. n=-20:1:20;
2. f=10*[0.9 .^n];
3. g=[cos(2*n*pi/16+pi/4)];
4. h=f.*g;
5. stem(n,h);
6. axis([-20 20 -30 70]);
77](https://image.slidesharecdn.com/minicursomatlabivsee2013semvideo-130627183525-phpapp01/85/Minicurso-Matlab-IVSEE-2013-UERJ-77-320.jpg)
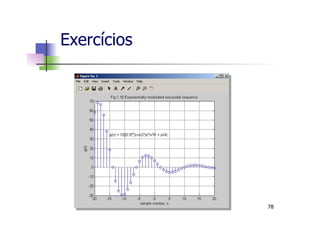

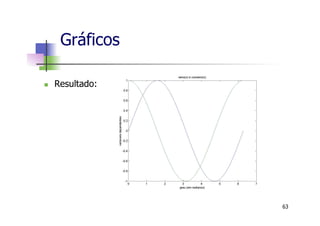
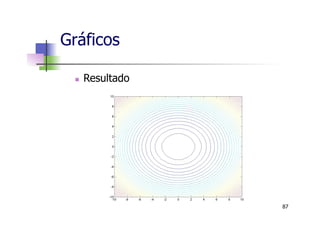
![n Gráficos 3D
n Gráficos de Superfícies - funcão mesh
>> v = linspace(-10,10,20);
>> [X, Y] = meshgrid(v,v);
>> Z = X.^2 + Y.^2;
>> mesh(X,Y,Z)
n Utilizamos a função meshgrid para gerar
X e Y como matrizes com valores repetidos
que são utilizadas para gerar a matriz Z.
Gráficos
80](https://image.slidesharecdn.com/minicursomatlabivsee2013semvideo-130627183525-phpapp01/85/Minicurso-Matlab-IVSEE-2013-UERJ-80-320.jpg)
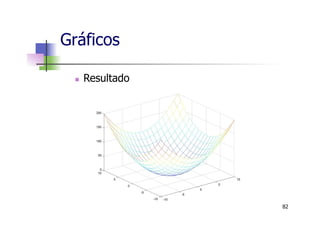
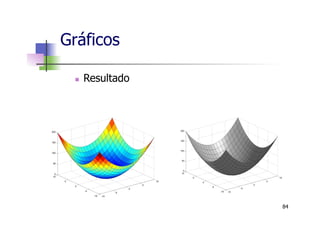
![n Gráficos 3D
n Gráficos de Superfícies - funcão mesh
>> v = linspace(-10,10,20);
>> [X, Y] = meshgrid(v,v);
>> Z = X.^2 + Y.^2;
>> mesh(X,Y,Z)
n Utilizamos a função meshgrid para gerar X e Y
como matrizes com valores repetidos que são
utilizadas para gerar a matriz Z.
Gráficos
81](https://image.slidesharecdn.com/minicursomatlabivsee2013semvideo-130627183525-phpapp01/85/Minicurso-Matlab-IVSEE-2013-UERJ-81-320.jpg)

















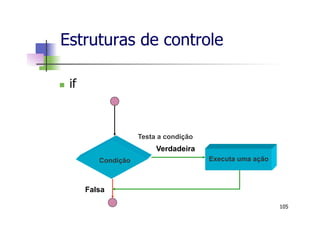

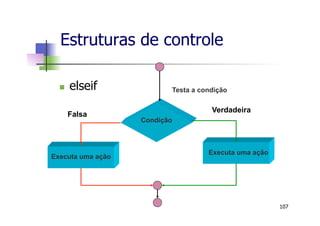



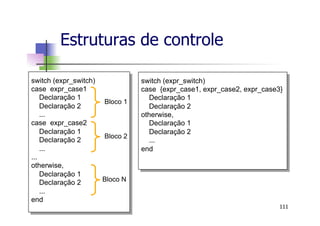



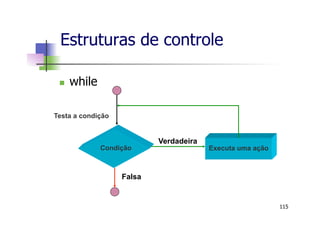

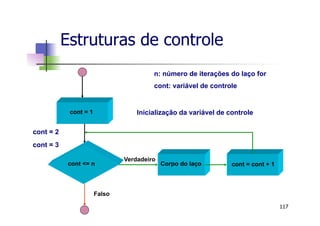










![Estruturas de controle
n Exercício: Implemente um algoritmo que
calcule a média e o desvio-padrão de um
conjunto de dados de entrada.
n dados de entrada: x = [3 4 5 -1]
n média:
n desvio-padrão:
128
x =
1
N
xi
i=1
N
!
s =
N xi
2
i=1
N
! " xi
i=1
N
!
#
$
%
&
'
(
2
N(N "1)](https://image.slidesharecdn.com/minicursomatlabivsee2013semvideo-130627183525-phpapp01/85/Minicurso-Matlab-IVSEE-2013-UERJ-128-320.jpg)
![n Cálculo da série de Fourier na forma complexa
Série de Fourier Complexa
129
X[k]=
1
N
x[n]e! jk"0n
n=1
N
#
"0 =
2!
N](https://image.slidesharecdn.com/minicursomatlabivsee2013semvideo-130627183525-phpapp01/85/Minicurso-Matlab-IVSEE-2013-UERJ-129-320.jpg)







![Funções definidas pelo usuário
n Forma geral
137
function [outarg1, outarg2, ...] = fname(inarg1, inarg2, ...)
% H1 comment line
% Other comment lines
...
(Executable code)
...
(return)
(end)](https://image.slidesharecdn.com/minicursomatlabivsee2013semvideo-130627183525-phpapp01/85/Minicurso-Matlab-IVSEE-2013-UERJ-137-320.jpg)








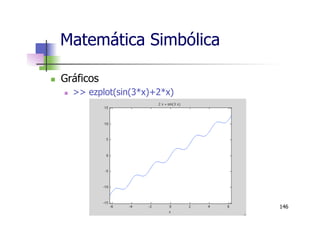
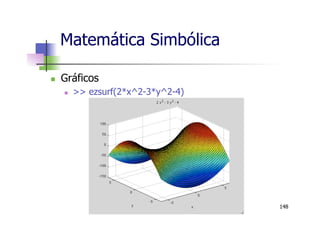
![Matemática Simbólica
n Gráficos
n >> ezplot(sin(3*x)+2*x,[1 2])
147](https://image.slidesharecdn.com/minicursomatlabivsee2013semvideo-130627183525-phpapp01/85/Minicurso-Matlab-IVSEE-2013-UERJ-147-320.jpg)