O documento apresenta os conceitos básicos de matrizes, incluindo sua declaração, preenchimento e acesso a elementos em linguagens de programação. É explicado como matrizes podem ter múltiplas dimensões e são acessadas usando índices para cada dimensão. Exemplos mostram como declarar e preencher matrizes bidimensionais e tridimensionais.

1. Aula 14
Prof. Gracon Lima

2. Principais Estruturas
Matrizes
Prof. Gracon Lima

3. Matrizes
• Introdução
– Linhas são enumeradas
de cima para baixo
– Colunas são enumeradas
da esquerda para a
direita
– Tabelas de m linhas e n
colunas são
denominadas matrizes
mxn
Prof. Gracon Lima

4. Matrizes
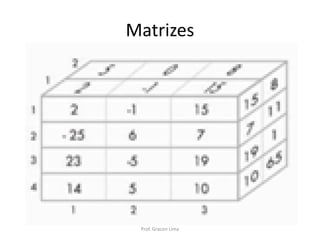
• Notação Geral
• Abreviadamente: A = [aij]mxn, em que i e j
representam a linha e a coluna que o elemento
ocupa
Representação
da Matriz
Representação
do Elemento
Representação
dos Índices
Prof. Gracon Lima

5. Matrizes Introdução
Como verificar a Nota de Espanhol do Aluno C?
• Aplicação
Prof. Gracon Lima

6. Matrizes
• Declaração de Matriz
– DECLARE nome[dimensão1,
dimensão2... Dimensãon] tipo
• Onde
– Dimensão1: quantidade de
elementos da dimensão1
– Dimensão2: quantidade de
elementos da dimensão2
– Dimensãon: quantidade de
elementos da dimensãon
– Tipo: tipo de dados da matriz
• Variável composta
homogênea
multidimensional
– Formada por uma sequencia
de variáveis, todas do mesmo
tipo, com o mesmo
identificador e alocadas
sequencialmente na memória
– O que distingue as variáveis
são os índices que
referenciam sua localização
dentro da estrutura
– Precisa de um indice para
cada uma de suas dimensões
Prof. Gracon Lima

7. Matrizes
• Exemplo de Matriz
bidimensional
– Nessa matriz
bidimensional o
tamanho da primeira
dimensão (linha) é 3 e o
da segunda (coluna) é 5
Prof. Gracon Lima

8. Matrizes
• Exemplo de Matriz
tridimensional
– Nessa matriz
tridimensional o
tamanho da primeira
dimensão (linha) é 4 e o
da segunda (coluna) é 6
e o da terceira
(profundudade) é 3
Prof. Gracon Lima

9. Matrizes
• Atribuindo valores a
uma matriz
– Cada elemento de uma
matriz pode armazenar
um valor
– Para armazenar , deve-se
executar uma atribuição
informando o número
das atribuições
Prof. Gracon Lima

10. Matrizes
• Preenchendo uma
matriz
– Para preencher, é
necessário identificar
todas as suas posições;
isso exige um índice para
cada dimensão da matriz
• No exemplo é
preenchida uma matriz
bidimensional de 3
linhas e 5 colunas
• Algoritmo:
– A variávei i varia dentro
do intervalo de 1 a 3
(nas linhas)
– Para cada valor de i, a
variável j varia de 1 a 5,
ou seja, as 5 colunas que
cada linha possui
Prof. Gracon Lima

11. Matrizes
Prof. Gracon Lima

12. Matrizes
Prof. Gracon Lima

13. Matrizes
Prof. Gracon Lima

14. Matrizes
• Matrizes
Tridimensionais
– São utilizadas três
variáveis contadoras
• i: controla as linhas
• j: controla as colunas
• k: controla a
profundidade
Prof. Gracon Lima

15. Matrizes
Prof. Gracon Lima

16. Matrizes
Prof. Gracon Lima

17. Matrizes
Prof. Gracon Lima

18. Matrizes
• Mostrando elementos de
uma matriz
– É necessário identificar as
posições
• Um índice para cada
dimensão da matriz
• No exemplo uma matriz
bidimensional com três
linhas e cinco colunas é
mostrada
– i: assume valores de 1 a 3
(exatamente nas linhas)
– J: i: assume valores de 1 a
5 (exatamente nas colunas)
Prof. Gracon Lima

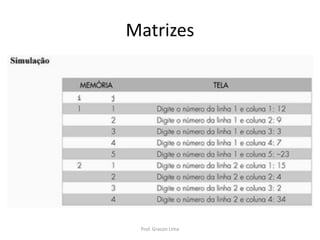
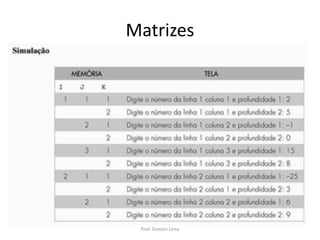
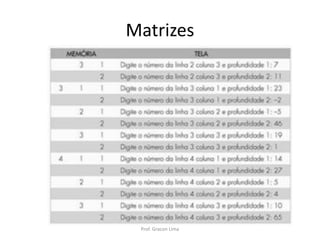
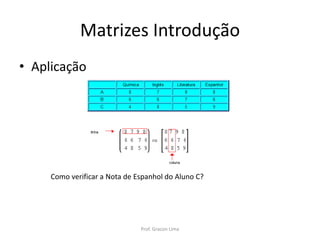
19. Matrizes no VisuAlg
• Declarando Matrizes :
– Declara o identificador
– Sinal de dois pontos
– A palavra vetor
– intervalo entre colchetes
• Utiliza-se “..” para
especificar um intervalo
maior
– Para cada dimensão utiliza
vírgula
– A palavra “de”
– O tipo de dados do vetor
• Apenas um tipo de dados
• Exemplo
algoritmo “vetor”
var
numero: vetor [1..10, 1..10]
de inteiro
Inicio
.
.
.
fimalgoritmo
Prof. Gracon Lima

20. Matrizes no VisuAlg
• Exemplo
algoritmo “vetor”
var
numero: vetor [1..10,
1..10] de inteiro
Inicio
para i de 1 ate 10 faca
para j de 1 ate 10 faca
escreva(numero[i, j])
fimalgoritmo
• Pode-se utilizar um laço
e percorrer o vetor com
o contador
– Os índices são acessados
colocando o nome
seguido das posições do
elemento
Prof. Gracon Lima