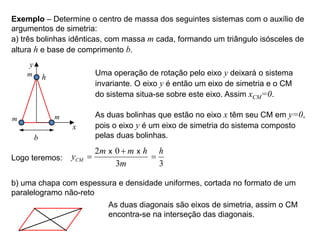
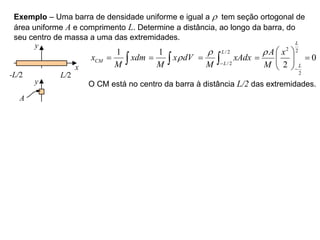
1) O documento discute conceitos de centro de gravidade, centro de massa e centroide, e apresenta exemplos de como calcular esses pontos para diferentes sistemas. 2) Alguns alunos tiveram dificuldades com certas questões que envolviam letras como dV, dL e dA. 3) O centro de massa de um cone homogêneo está localizado a 1/3 da altura do cone quando medido do fundo.

1. AULA 01 – Centro de Gravidade
Centro de Massa
Centroide
Prof. Thiago R. Rodrigues

2. Objetivo desta aula
 Entender os Conceitos de “Centro de Gravidade”,
“Centro de Massa” e “Centroide”.
 Resolver diferentes tipos de problemas.

3. Comentários e Sugestões
1 - No exercício da caixa sem tampa, meu resultado não tinha
em opção, achei cm como
2 - Não consegui fazer a 3 professor !!
3 - Algumas questões foram desafiadoras, mas o teste foi bem
condizente com o assunto
4 - o fato de usar letras em alguns deles é bem útil para o
aprendizado
5 - O teste foi de pouca utilidade pois não consegui encontrar
sequer os assuntos abordados nas questões para estudar antes
de resolve-las.

4. Comentários e Sugestões
6 - Não consegui resolver as questões do livro pois tive não
consegui entender o que seriam dV, dL, dA.
7 - Gostaria de ter tido aulas sobre o assunto antes de fazer um
quiz onde a minha nota está em jogo.
3 – Pouco tempo para resolver os teste.
4 - o fato de usar letras em alguns deles é bem útil para o
aprendizado
5 - O teste foi de pouca utilidade pois não consegui encontrar
sequer os assuntos abordados nas questões para estudar antes
de resolve-las.

5. Sistemas com um número qualquer de partículas
Centro de massa
Consideremos o sistema constituído de N partículas i, i=1,2,3,...,N, cujas massas
são mi. O centro de massa do sistema é o ponto definido pelo vetor
1
1 N
CM i i
i
m
M 
 
r r
onde é a massa total do sistema.
1
N
i
i
M m

 
Exemplo – Calcule o centro de massa de um sistema de quatro partículas
iguais dispostas nos vértices de um quadrado de lado L.
y
x
L
L
m
m
m
m
1
(0 0 )
4
CM
x mL mL
m
   
2
L

1
(0 0)
4
CM
y mL mL
m
   
2
L

O CM coincide com o centro geométrico do quadrado.

6. Operação de simetria sobre um sistema é qualquer operação após a qual o
sistema pareça exatamente o mesmo.
Simetria
1
1
1
2 2
2
3
3
3
M1
M2
M3
E C1 C2
1
1 1
2 2
2
3
3
3
M1
M2 M3
(a) (b)
(d) (e) (f)
(c )
Sejam três bolinhas idênticas dispostas nos vértices de um triângulo equilátero.
Se uma operação de simetria for
feita sem que você veja, você
não será capaz de perceber que
o sistema foi mudado.
Este sistema tem seis operacões de simetria, que são mostradas na figura abaixo.

7. Simetria no cálculo de centro de massa
Quando efetuamos uma operação de simetria sobre um determinado corpo, estamos
simplesmente permutando suas partículas.
1
1 N
CM i i
i
m
M 
 
r r
Neste caso, o somatório da equação abaixo que exprime a posição do CM sofrerá
um mero rearranjo de seus termos e permanecerá com resultado inalterado.
O mesmo argumento pode ser estendido para a integral da equação abaixo.
1
CM dm
M
 
r r
 Posição do CM para um sistema de N partículas
 Posição do CM para um corpo extenso
Ou seja, uma operação de simetria de um sistema não pode deslocar o seu CM.
Se a operação de simetria for uma rotação, os únicos pontos fixos estão sobre o
eixo de rotação. Logo, se um sistema possuir um eixo de simetria, o seu CM
necessariamente se situa sobre tal eixo
Se o sistema possuir dois eixos de simetria, o CM se situa na interseção dos eixos.

8. Exemplo  Determine o centro de massa dos seguintes sistemas com o auxílio de
argumentos de simetria:
a) três bolinhas idênticas, com massa m cada, formando um triângulo isósceles de
altura h e base de comprimento b.
y
x
h
b
m
m
m Uma operação de rotação pelo eixo y deixará o sistema
invariante. O eixo y é então um eixo de simetria e o CM
do sistema situa-se sobre este eixo. Assim xCM=0.
As duas bolinhas que estão no eixo x têm seu CM em y=0,
pois o eixo y é um eixo de simetria do sistema composto
pelas duas bolinhas.
Logo teremos:
2 0
3
CM
m m h
y
m


x x
3
h

b) uma chapa com espessura e densidade uniformes, cortada no formato de um
paralelogramo não-reto
As duas diagonais são eixos de simetria, assim o CM
encontra-se na interseção das diagonais.

9. Questões com menos de 30% de Acerto

10. c) uma caixa cúbica de lado a, com paredes de mesma espessura e mesmo
material, sem a tampa superior.
a
y
A caixa fica invariante a rotacões de p/2 em torno do
eixo y, perpendicular à base e ao quadrado da tampa
ausente, passando pelos seus centros.
Logo, y é um eixo de simetria e o CM do sistema situa-se
sobre ele.
0
Escolhemos o centro da caixa como a origem das
coordenadas.
O CM de cada face está em seu centro de simetria.
Para as faces laterais, isto corresponde a y=0 e para a face inferior a y=-a/2.
Supondo que cada face tenha massa m, o CM da caixa cúbica sem tampa superior
será então:
4 0 (- / 2)
5
CM
m m a
y
m


x x
10
a
 

11. Questões com menos de 30% de Acerto

12. Centroide
Consideremos a densidade constante
onde é a massa total do sistema.
1
CM dm
M
 
r r Onde,
Centroide de volume

13. Centro de Gravidade
Consideremos a densidade constante
Onde,

14. Exemplo – Uma barra de densidade uniforme e igual a r tem seção ortogonal de
área uniforme A e comprimento L. Determine a distância, ao longo da barra, do
seu centro de massa a uma das extremidades.
y
x
-L/2 L/2
1
CM
x xdm
M
 
1
x dV
M
r
 
/2
/2
L
L
xAdx
M
r

 
2 2
2
0
2
L
L
A x
M
r

 
 
 
 
O CM está no centro da barra à distância L/2 das extremidades.
y
A

15. Questões com menos de 30% de Acerto

16. Exemplo – Duas barras de mesmo comprimento L e mesma seção ortogonal de
área uniforme A, com densidades uniformes r1 e r2, são soldadas de modo a
compor uma barra de comprimento 2L, como mostra a Figura abaixo. Determine a
posição do centro de massa da barra composta.
y
x
-L L
r1 r2
1
CM
x xdm
M
 
1
x dV
M
r
 
1 L
L
x Adx
M
r

 
0
2 2
1 2
0
2 2
L
L
A A
x x
M M
r r

   
 
   
   
0
1 2
0
1 1 L
CM L
x x Adx x Adx
M M
r r

 
 
2 2
1 2
2 2
A A
L L
M M
r r
  
2
2 1
( )
2
CM
A L
x
M
r r
  Mas 1 2 1 1 2 2 1 2
( )
M M M V V AL
r r r r
     
(1) (2)
(2) em (1):
2
2 1
2 1
( )
2 ( )
CM
AL
x
AL
r r
r r



2 1
2 1
( )
2 ( )
CM
L
x
r r
r r

 

*
* Solução alternativa:
0
1 2
1 2
0
1 2
1 1
L
CM L
M M
x x Adx x Adx
M M M M
r r

 
 
xCM1 xCM2
 
1 1 2 2
1
CM CM
M x M x
M
 

17. 2 1
( )
2
CM
L
x M M
M
 
* Solução alternativa – continuação:
2 1
2 1
( )
2 ( )
M M
L
M M



2 1
2 1
( )
2 ( )
L V
V
r r
r r



2 1
2 1
( )
2 ( )
CM
L
x
r r
r r

 

como obtido anteriormente.
A equação diz que, sabendo-se as posições dos
CM de duas partes com massas M1 e M2 de um sistema, podemos considerar
estas massas concentradas em seus respectivos centros de massas e usar a
equação para o CM de um sistema de duas partículas para encontrar o CM do
sistema completo.
1 1 2 2
1
( )
CM CM CM
x M x M x
M
 
Esta é uma regra geral. Vale para mais do que uma dimensão e também para
sistemas compostos de várias partes ao invés de apenas duas.
1 2
1
2 2
M L M L
M

 
 
 
 
 
1 1 2 2
1
CM CM CM
x M x M x
M
 

18. Exemplo - Determine o centroide de área de um triangulo de base b e altura h.
y
h
dy
b

19. Exemplo - Determine o centro de massa de um cone homogêneo de base circular
de raio R e altura h.
y
R
h
r
dy y
O cone tem densidade uniforme (é homogêneo), assim seu
CM estará em algum ponto do eixo de simetria (y).
1
CM
y ydm
M
 
1
y dV
V
r
r
 
1
ydV
V
 
Mas dV=pr2dy.
2
0
h
CM
y r ydy
V
p
  
Como r varia em função de y, por semelhança de triângulos temos:
r y
R h

R
r y
h
 
(1)
(2)
(2) em (1):
2
0
h
CM
R
y y ydy
V h
p  
  
 

2
3
2 0
h
R
y dy
Vh
p
 
2 4
2
0
4
h
R y
Vh
p  
  
 
2 4
2
4
R h
Vh
p

2 2
4
R h
V
p

Como dV=pr2dy
2
R
dV y dy
h
p
 
   
 
2
2
2 0
h
R
V y dy
h
p
  
2 3
2
3
R h
h
p

2
1
3
R h
p

2 2
2
3
4
CM
R h
y
R h
p
p
 
3
4
h
