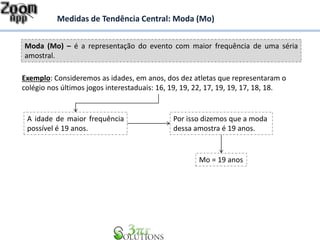
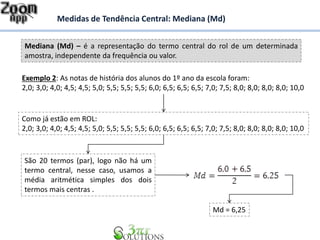
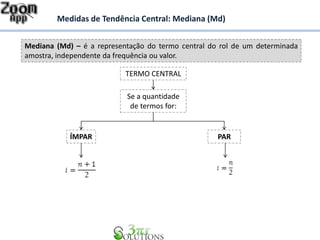
O documento apresenta os conceitos de moda e mediana como medidas de tendência central de uma amostra. A moda é o valor que mais se repete na amostra, enquanto a mediana é o valor do termo central quando os dados são organizados em ordem crescente. Exemplos ilustram como calcular a moda e a mediana em diferentes conjuntos de dados.

1. Estatística:

2. Estatística:
1. Introdução à Estatística;
2. Conceitos:
3. Medidas Centrais:
a. Conceito;
b. Média Aritmética Simples;
c. Média Aritmética Ponderada;
d. Moda;
e. Mediana;

3. Moda (Mo) – é a representação do evento com maior frequência de uma séria
amostral.
Medidas de Tendência Central: Moda (Mo)
Exemplo: Consideremos as idades, em anos, dos dez atletas que representaram o
colégio nos últimos jogos interestaduais: 16, 19, 19, 22, 17, 19, 19, 17, 18, 18.
A idade de maior frequência
possível é 19 anos.
Por isso dizemos que a moda
dessa amostra é 19 anos.
Mo = 19 anos

4. Estatística:
1. Introdução à Estatística;
2. Conceitos:
3. Medidas Centrais:
a. Conceito;
b. Média Aritmética Simples;
c. Média Aritmética Ponderada;
d. Moda;
e. Mediana;

5. Mediana (Md) – é a representação do termo central do rol de um determinada
amostra, independente da frequência ou valor.
Medidas de Tendência Central: Mediana (Md)

6. Mediana (Md) – é a representação do termo central do rol de um determinada
amostra, independente da frequência ou valor.
Medidas de Tendência Central: Mediana (Md)
Exemplo 1: As estaturas, em centímetros, dos cinco jogadores da equipe de
basquetebol do nosso colégio em cm são: 184; 179; 190; 181; 178.

7. Mediana (Md) – é a representação do termo central do rol de um determinada
amostra, independente da frequência ou valor.
Medidas de Tendência Central: Mediana (Md)
Exemplo 1: As estaturas, em centímetros, dos cinco jogadores da equipe de
basquetebol do nosso colégio em cm são: 184; 179; 190; 181; 178.
Colocando em ROL, teremos:
178, 179, 181, 184, 190

8. Mediana (Md) – é a representação do termo central do rol de um determinada
amostra, independente da frequência ou valor.
Medidas de Tendência Central: Mediana (Md)
Exemplo 1: As estaturas, em centímetros, dos cinco jogadores da equipe de
basquetebol do nosso colégio em cm são: 184; 179; 190; 181; 178.
Colocando em ROL, teremos:
178, 179, 181, 184, 190
São cinco termos, assim o termo 181
representa a mediana.

9. Mediana (Md) – é a representação do termo central do rol de um determinada
amostra, independente da frequência ou valor.
Medidas de Tendência Central: Mediana (Md)
Exemplo 1: As estaturas, em centímetros, dos cinco jogadores da equipe de
basquetebol do nosso colégio em cm são: 184; 179; 190; 181; 178.
Colocando em ROL, teremos:
178, 179, 181, 184, 190
São cinco termos, assim o termo 181
representa a mediana.
Md = 181 cm

10. Mediana (Md) – é a representação do termo central do rol de um determinada
amostra, independente da frequência ou valor.
Medidas de Tendência Central: Mediana (Md)
Exemplo 2: As notas de história dos alunos do 1º ano da escola foram:
2,0; 3,0; 4,0; 4,5; 4,5; 5,0; 5,5; 5,5; 5,5; 6,0; 6,5; 6,5; 6,5; 7,0; 7,5; 8,0; 8,0; 8,0; 8,0; 10,0

11. Mediana (Md) – é a representação do termo central do rol de um determinada
amostra, independente da frequência ou valor.
Medidas de Tendência Central: Mediana (Md)
Exemplo 2: As notas de história dos alunos do 1º ano da escola foram:
2,0; 3,0; 4,0; 4,5; 4,5; 5,0; 5,5; 5,5; 5,5; 6,0; 6,5; 6,5; 6,5; 7,0; 7,5; 8,0; 8,0; 8,0; 8,0; 10,0
Como já estão em ROL:
2,0; 3,0; 4,0; 4,5; 4,5; 5,0; 5,5; 5,5; 5,5; 6,0; 6,5; 6,5; 6,5; 7,0; 7,5; 8,0; 8,0; 8,0; 8,0; 10,0

12. Mediana (Md) – é a representação do termo central do rol de um determinada
amostra, independente da frequência ou valor.
Medidas de Tendência Central: Mediana (Md)
Exemplo 2: As notas de história dos alunos do 1º ano da escola foram:
2,0; 3,0; 4,0; 4,5; 4,5; 5,0; 5,5; 5,5; 5,5; 6,0; 6,5; 6,5; 6,5; 7,0; 7,5; 8,0; 8,0; 8,0; 8,0; 10,0
Como já estão em ROL:
2,0; 3,0; 4,0; 4,5; 4,5; 5,0; 5,5; 5,5; 5,5; 6,0; 6,5; 6,5; 6,5; 7,0; 7,5; 8,0; 8,0; 8,0; 8,0; 10,0
São 20 termos (par), logo não há um
termo central, nesse caso, usamos a
média aritmética simples dos dois
termos mais centras .

13. Mediana (Md) – é a representação do termo central do rol de um determinada
amostra, independente da frequência ou valor.
Medidas de Tendência Central: Mediana (Md)
Exemplo 2: As notas de história dos alunos do 1º ano da escola foram:
2,0; 3,0; 4,0; 4,5; 4,5; 5,0; 5,5; 5,5; 5,5; 6,0; 6,5; 6,5; 6,5; 7,0; 7,5; 8,0; 8,0; 8,0; 8,0; 10,0
Como já estão em ROL:
2,0; 3,0; 4,0; 4,5; 4,5; 5,0; 5,5; 5,5; 5,5; 6,0; 6,5; 6,5; 6,5; 7,0; 7,5; 8,0; 8,0; 8,0; 8,0; 10,0
São 20 termos (par), logo não há um
termo central, nesse caso, usamos a
média aritmética simples dos dois
termos mais centras .

14. Mediana (Md) – é a representação do termo central do rol de um determinada
amostra, independente da frequência ou valor.
Medidas de Tendência Central: Mediana (Md)
Exemplo 2: As notas de história dos alunos do 1º ano da escola foram:
2,0; 3,0; 4,0; 4,5; 4,5; 5,0; 5,5; 5,5; 5,5; 6,0; 6,5; 6,5; 6,5; 7,0; 7,5; 8,0; 8,0; 8,0; 8,0; 10,0
Como já estão em ROL:
2,0; 3,0; 4,0; 4,5; 4,5; 5,0; 5,5; 5,5; 5,5; 6,0; 6,5; 6,5; 6,5; 7,0; 7,5; 8,0; 8,0; 8,0; 8,0; 10,0
São 20 termos (par), logo não há um
termo central, nesse caso, usamos a
média aritmética simples dos dois
termos mais centras .
Md = 6,25

15. Mediana (Md) – é a representação do termo central do rol de um determinada
amostra, independente da frequência ou valor.
Medidas de Tendência Central: Mediana (Md)
Se a quantidade
de termos for:
ÍMPAR PAR
TERMO CENTRAL

16. FIM da Apresentação!