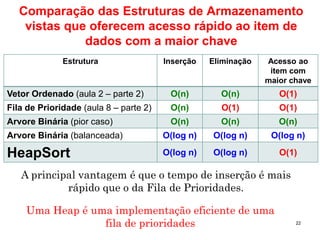
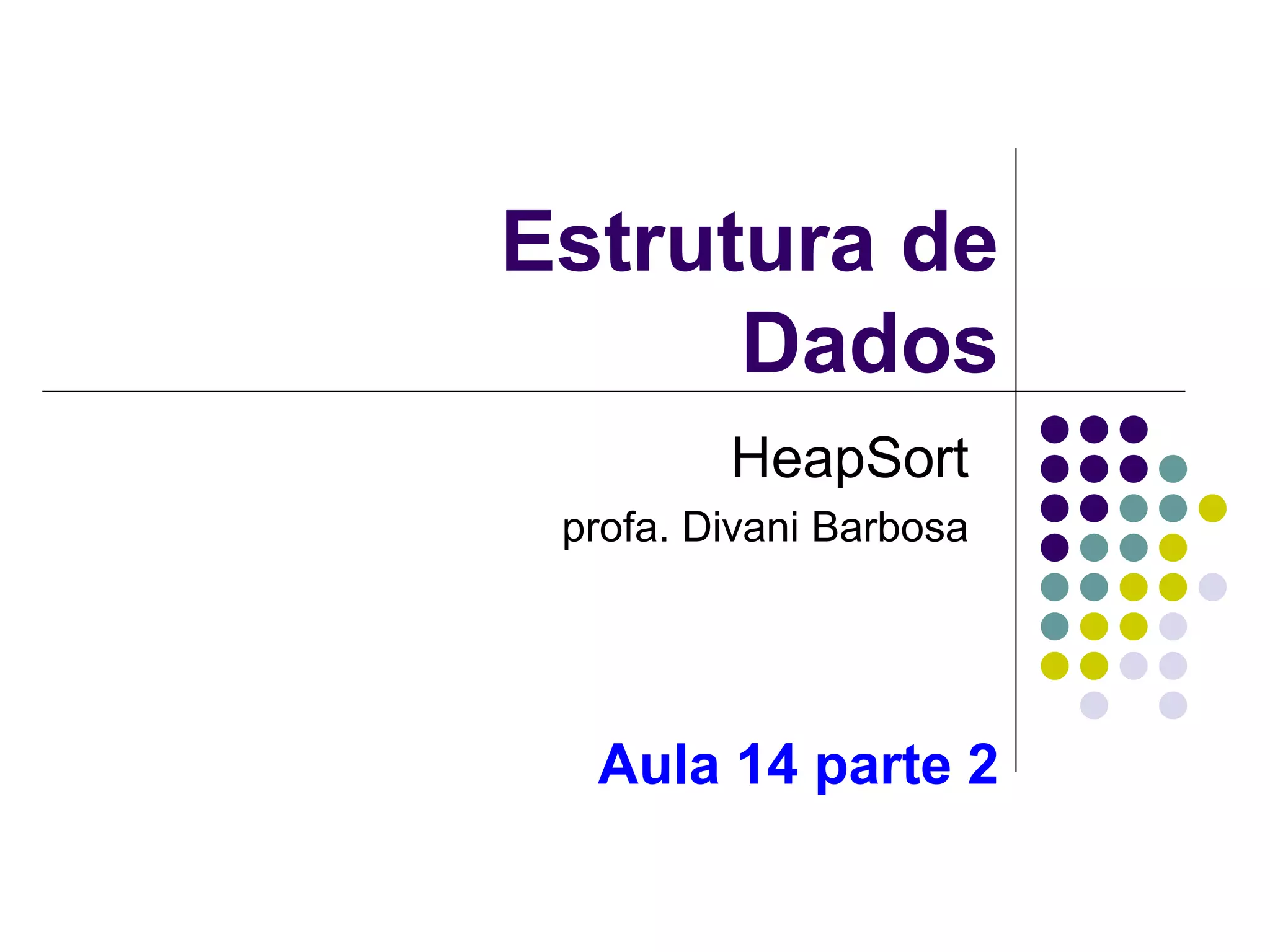
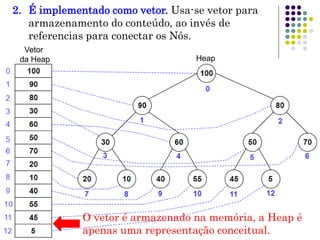
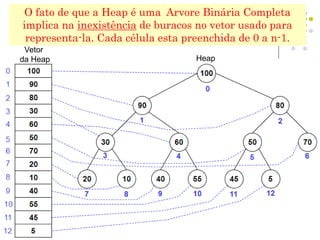
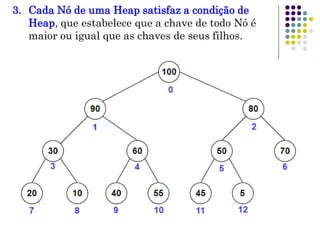
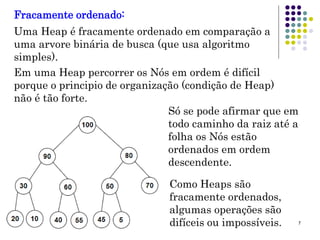
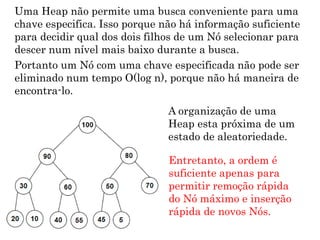
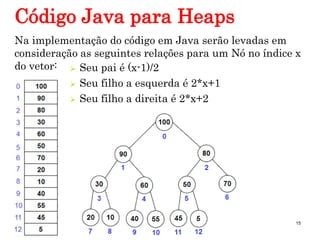
A Heap é uma estrutura de dados eficiente para implementar filas de prioridade, oferecendo acesso rápido ao maior item e remoção/inserção em tempo O(logN). Uma Heap é implementada como um vetor que representa uma árvore binária completa, com a raiz no índice zero e o último item no índice n-1, onde cada nó tem uma chave menor que seus pais e maior que seus filhos.

1. Estrutura de
Dados
HeapSort
profa. Divani Barbosa
Aula 14 parte 2

2. 2
Heaps
Uma Heap é uma estrutura de dados do tipo árvore
binária balanceada. Sendo assim, ela oferece inserção e
eliminação num tempo O(log n).
Ela é o tipo de estrutura ideal para aplicações que
necessitam de acesso rápido ao item de dados com a menor
e maior chave.
Comparada com uma Fila de Prioridades, a Heap não é tão
rápida na eliminação, porém, é muito mais rápido para
inserção.
É o método ideal para implementar filas de prioridades
onde velocidade seja importante e haja muita inserções.
Estrutura de Armazenamento de Dados de
Propósito Especial

3. Uma Heap é uma arvore binária com as seguintes
características:
1. É completo. Isso significa que ele fica
completamente preenchido, lendo da esquerda
para direita cada linha, embora a última linha não
precise estar cheia.
Exemplo:
Arvore binária completa Arvore binária incompleta

4. Vetor
da Heap Heap
2. É implementado como vetor. Usa-se vetor para
armazenamento do conteúdo, ao invés de
referencias para conectar os Nós.
O vetor é armazenado na memória, a Heap é
apenas uma representação conceitual.

5. Vetor
da Heap Heap
O fato de que a Heap é uma Arvore Binária Completa
implica na inexistência de buracos no vetor usado para
representa-la. Cada célula esta preenchida de 0 a n-1.

6. 3. Cada Nó de uma Heap satisfaz a condição de
Heap, que estabelece que a chave de todo Nó é
maior ou igual que as chaves de seus filhos.

7. 7
Fracamente ordenado:
Uma Heap é fracamente ordenado em comparação a
uma arvore binária de busca (que usa algoritmo
simples).
Em uma Heap percorrer os Nós em ordem é difícil
porque o principio de organização (condição de Heap)
não é tão forte.
Só se pode afirmar que em
todo caminho da raiz até a
folha os Nós estão
ordenados em ordem
descendente.
Como Heaps são
fracamente ordenados,
algumas operações são
difíceis ou impossíveis.

8. 8
Uma Heap não permite uma busca conveniente para uma
chave especifica. Isso porque não há informação suficiente
para decidir qual dos dois filhos de um Nó selecionar para
descer num nível mais baixo durante a busca.
Portanto um Nó com uma chave especificada não pode ser
eliminado num tempo O(log n), porque não há maneira de
encontra-lo.
A organização de uma
Heap esta próxima de um
estado de aleatoriedade.
Entretanto, a ordem é
suficiente apenas para
permitir remoção rápida
do Nó máximo e inserção
rápida de novos Nós.

9. 9
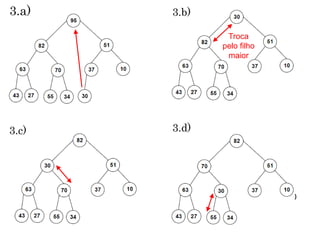
Remoção significa remover um Nó com a chave
máxima. Esse Nó é sempre a raiz e ela esta no índice
zero do vetor da Heap, portanto remove-lo é fácil.
Remoção
O problema é que restara um “buraco” que tem de ser
preenchido. Para isso usa-se os seguintes passos:
1. Remova a raiz
2. Mova o ultimo Nó para raiz
vHeap[0] = vHeap[n-1];
n--;
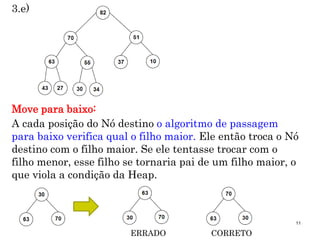
3. Passe para baixo o ultimo Nó até que ele fique abaixo de
um Nó maior e acima de um Nó menor.

10. 10
3.a) 3.b)
Troca
pelo filho
maior
3.c) 3.d)

11. 11
3.e)
A cada posição do Nó destino o algoritmo de passagem
para baixo verifica qual o filho maior. Ele então troca o Nó
destino com o filho maior. Se ele tentasse trocar com o
filho menor, esse filho se tornaria pai de um filho maior, o
que viola a condição da Heap.
Move para baixo:
ERRADO CORRETO

12. 12
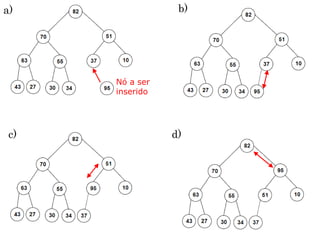
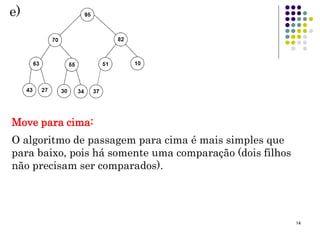
A inserção usa passagem para cima, ao invés de para
baixo. Inicialmente o Nó a ser inserido é colocado na
primeira posição aberta no final do vetor.
Inserção
vHeap[n] = novo;
n++;
Logo após, caso se faça necessário para se manter a
condição de Heap, o novo Nó será passado para cima até
que fique abaixo de um Nó com uma chave maior e acima
de um Nó com uma chave menor.

13. 13
Nó a ser
inserido
b)
c) d)
a)

14. 14
e)
O algoritmo de passagem para cima é mais simples que
para baixo, pois há somente uma comparação (dois filhos
não precisam ser comparados).
Move para cima:

15. 15
Código Java para Heaps
Na implementação do código em Java serão levadas em
consideração as seguintes relações para um Nó no índice x
do vetor:  Seu pai é (x-1)/2
 Seu filho a esquerda é 2*x+1
 Seu filho a direita é 2*x+2

16. 16
private int[] vHeap;
private int tam_max;
private int n;
Classe Heap:
Campos Construtor
public Heap(int v) {
tam_max = v;
n = 0;
vHeap = new int[tam_max];
}
Métodos
vazio: retorna verdadeiro se vazio.
cheio: retorna verdadeiro se cheio.
insere: insere itens.
remove: remove itens retornando-os.
MoveAcima e MoveAbaixo: move itens
(usado pelos métodos insere e remove).

17. 17
class Heap {
private int[] vHeap;
private int tam_max;
private int n;
public Heap(int v) {
tam_max = v;
n = 0;
vHeap = new int[tam_max];
}
public boolean vazio() { return n==0; }
public boolean cheio() { return n==(tam_max-1); }
public boolean insere(int v) {
if (cheio()) return false;
vHeap[n] = v;
MoveAcima(n); n++;
return true;
}

18. 18
public int remove() { // Elimina item com a chave máxima
int root = vHeap[0]; // (assume Heap não vazia)
vHeap[0] = vHeap[n-1];
n--;
MoveAbaixo(0);
return root;
}
public void MoveAcima(int indice) {
int pai = (indice-1)/2;
int guarda = vHeap[indice];
while (índice > 0 && vHeap[pai] < guarda)
{
vHeap[indice] = vHeap[pai];
indice = pai;
pai = (pai-1)/2;
}
vHeap[indice] = guarda;
}

19. 19
public void MoveAbaixo(int indice) {
int filhoMaior, filhoEsq, filhoDir;
int topo = vHeap[indice];
while (indice < n/2) { // enquanto No tiver pelo menos um filho
filhoEsq = 2*indice+1;
filhoDir = filhoEsq+1;
if (filhoDir<n && vHeap[filhoEsq] < vHeap[filhoDir])
filhoMaior = filhoDir;
else
filhoMaior = filhoEsq;
if (topo >= vHeap[filhoMaior]) break;
vHeap[indice] = vHeap[filhoMaior];
indice = filhoMaior;
}
vHeap[indice] = topo;
}
} // fim classe Heap

20. 20
Exemplo de uso da Classe Heap:
class HeapApp {
public static void main(String[] args) {
Heap h = new Heap(20);
System.out.println(" Inserindo itens: 90, 60, 80, 30,
55, 50, 70, 20, 10, 40, 5, 45");
h.insere(90); h.insere(60); h.insere(80);
h.insere(30); h.insere(55); h.insere(50); h.insere(70);
h.insere(20); h.insere(10); h.insere(40); h.insere(5);
h.insere(45);
System.out.print(" Removendo itens: ");
while (!h.vazio()) System.out.print(h.remove() + " ");
System.out.println();
}
}

21. Comparação das Estruturas de Armazenamento
vistas que oferecem acesso rápido ao item de
dados com a maior chave
21arvore binária
balanceada
arvore binária
degenerada
arvore binária
degenerada
(pior caso)
Estrutura Inserção Eliminação Acesso ao
item com
maior chave
Vetor Ordenado (aula 2 – parte 2) O(n) O(n) O(1)
Fila de Prioridade (aula 8 – parte 2) O(n) O(1) O(1)
Arvore Binária (pior caso) O(n) O(n) O(n)
Arvore Binária (balanceada) O(log n) O(log n) O(log n)

22. 22
Estrutura Inserção Eliminação Acesso ao
item com
maior chave
Vetor Ordenado (aula 2 – parte 2) O(n) O(n) O(1)
Fila de Prioridade (aula 8 – parte 2) O(n) O(1) O(1)
Arvore Binária (pior caso) O(n) O(n) O(n)
Arvore Binária (balanceada) O(log n) O(log n) O(log n)
HeapSort O(log n) O(log n) O(1)
Comparação das Estruturas de Armazenamento
vistas que oferecem acesso rápido ao item de
dados com a maior chave
A principal vantagem é que o tempo de inserção é mais
rápido que o da Fila de Prioridades.
Uma Heap é uma implementação eficiente de uma
fila de prioridades

23. 23
Resumo
 A Heap é a implementação eficiente de uma fila de
prioridades;
 Uma Heap oferece acesso rápido ao maior item
(sempre está na raiz)
 Uma Heap oferece remoção do maior e inserção de
itens em tempo O(logN)
 A Heap não suporta travessia ordenada de dados,
localizar ou eliminar item com chave especifica.
 A Heap é implementada como um vetor
representando uma arvore binária completa. A raiz
esta no índice zero e o ultimo item no item n-1.
 Cada nó tem uma chave menor que seus pais e
maior que seus filhos

24. 24
Aplicações
 Escalonamento de tarefas em computadores onde
alguns programas e atividades devem ser
executados antes que outros, e, portanto, recebem
uma prioridade mais alta.

25. 25
 Sistemas de Armas (cruzador de uma esquadra)
Em um cruzador de guerra diversas ameaças, como
aviões, misseis, submarinos, etc.) devem ser
detectadas e priorizadas.
Por exemplo: Um míssil que esteja a uma distancia
curta do cruzador recebe uma prioridade mais alta
que um avião a longa distancia)

26. 26
 Sistema controlador de vôo

27. 27
Atividades
1. Modifique o método de remoção de itens da classe Heap
para que o mesmo verifique antes se a Heap esta vazia.
2. Trabalho 2 - Exercício 7. Um problema da implementação
da Heap baseado em vetor é o tamanho fixo do vetor. Se os
seus dados extrapolarem o vetor, você precisará expandi-lo.
Evite esse problema implementando no algoritmo de inserção
uma verificação, caso o usuário da classe estiver para
transbordar o vetor interno, o algoritmo de inserção criará um
novo vetor com o dobro do tamanho atual, copiará o conteúdo
do antigo vetor para o novo vetor e então inserirá o novo item.
Esse processo inteiro seria invisível para o usuário da classe.