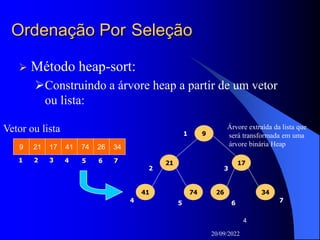
O documento descreve o algoritmo de ordenação heapsort. Ele utiliza uma estrutura de dados heap para ordenar os elementos de um vetor de forma eficiente em tempo O(n log n). O heapsort constrói primeiro um heap máximo a partir do vetor e então retira sucessivamente os elementos maiores da raiz para ordená-los.

1. 20/09/2022
1
Ordenação Por Seleção
 Método Heap-Sort
Este método introduz outra técnica em
algoritmos, o uso de uma estrutura de dados
chamada “HEAP” ou “Monte” para gerenciar
informações durante a execução do
algoritmo.
A estrutura de dados “Heap” não é útil
apenas para o Heap-Sort, ela também cria
uma eficiente fila de prioridades.

2. 20/09/2022
2
Ordenação Por Seleção
 Método heap-sort.
 Utiliza a seleção em árvore binária para a
obtenção dos elementos de um vetor (ou lista
em python) na ordem desejada.
Possui duas fases distintas:
 Construção da árvore binária heap com os
elementos do vetor (ou lista) ;
 Usa-se este heap construído para a seleção
dos elementos na ordem desejada.

3. 20/09/2022
3
Ordenação Por Seleção
 Método heap-sort:
Uma árvore binária Heap é uma árvore
em que os nós ascendentes são sempre
maiores que os descendentes, ou seja o nó
pai é sempre maior que os nós filhos.
Nó Pai Nó Filho
>

4. 20/09/2022
4
 Método heap-sort:
Construindo a árvore heap a partir de um vetor
ou lista:
Ordenação Por Seleção
9 26
21 41 74
17 34
3
Vetor ou lista
1 2 4 5 6 7
9
17
34
26
21
41 74
1
2
4 5 6 7
Árvore extraída da lista que
será transformada em uma
árvore binária Heap
3

5. 20/09/2022
5
Ordenação Por Seleção
- O algoritmo testa se o Nó Pai é maior que os nós filhos, se for ele
não faz nada.
- Caso contrário, ele testa qual filho é maior (se o esquerdo ou
direito) e o troca pelo Nó Pai.
9
17
34
26
21
41 74
1
2
4 5 6 7
3
9
34
17
26
74
41 21
1
2
4 5 6 7
3

6. 20/09/2022
6
Ordenação Por Seleção
- Continuando a montar a árvore heap:
74
34
17
26
9
41 21
1
2
4 5 6 7
3
9
34
17
26
74
41 21
1
2
4 5 6 7
3

7. 20/09/2022
7
Ordenação Por Seleção
74
34
17
26
41
9 21
1
2
4 5 6 7
3
- Está é uma árvore Heap, todos os nós descendentes são menores
que os nós ascendentes, ou seja os nós pais maiores que os nós
filhos.
- Outra propriedade importante é que na Árvore Heap, a raiz
principal terá sempre o maior elemento da árvore.
VEJA PORQUE!!!

8. 20/09/2022
8
Ordenação Por Seleção
74
34
17
26
41
9 21
1
2
4 5 6 7
3
- Agora vou ordenar a lista em ordem crescente, retirando a raiz da
Árvore Heap
41
34
74
26
21
9 17
1
2
4 5 6 7
3
34
26
74
41
21
9 17
1
2
4 5 6 7
3
Cada vez que extrai a raiz principal, chama-se a função Max_Heap,
que garante a maior chave sempre no topo, é um Heap Máximo.

9. 20/09/2022
9
34
26
74
41
21
9 17
1
2
4 5 6 7
3
- Agora vou ordenar a lista em ordem crescente, retirando a raiz da
Árvore Heap
26
17
74
41
21
9 34
1
2
4 5 6 7
3
21
17
74
41
9
26 34
1
2
4 5 6 7
3
LEMBRE-SE: Cada vez que extrai a raiz principal,
chamamos a função Max_Heap.
Ordenação Por Seleção

10. 20/09/2022
10
17
21
74
41
9
26 34
1
2
4 5 6 7
3
- Agora vou ordenar a lista em ordem crescente, retirando a raiz da
Árvore Heap
4 5 6 7
9
21
74
41
17
26 34
1
2 3
Ordenação Por Seleção
= 9 41
17 26 34
21 74
3
1 2 4 5 6 7
Lista em ordem crescente

11. 20/09/2022
11
Ordenação Por Seleção
 Método heap-sort (Considerações):
 É um algoritmo ótimo;
 Complexidade de Tempo: O(n . log n);
 Não requer espaço extra de memória, por isso é mais
Rápido que o Merge-Sort;
 Na prática é um pouco mais lento do que o Quick-Sort.

12. 20/09/2022
12
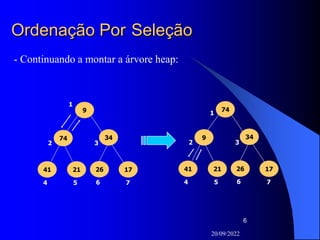
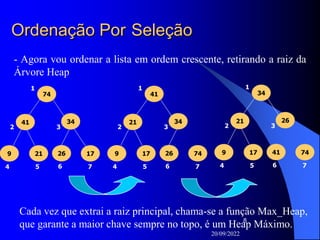
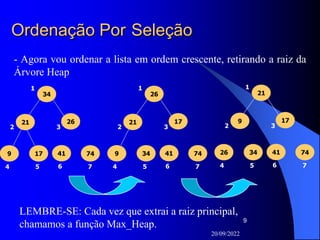
Ordenação Por Seleção
 Função Max_Heap:
Mantém a propriedade de Heap Máximo.
Função Max_Heap(A,i)
L left(i)
R right(i)
Se L <= tamanho_heap[A] E A[L] > A[i]
Então maior L
Senão maior i
Se R <= tamanho_heap[A] E A[R] > A[maior]
Então maior R
Se maior = i
Então trocar A[i] A[maior]
Max_Heap(A,maior)

13. 20/09/2022
13
Ordenação Por Seleção
 Função Build_Max_Heap:
Constói a Árvore com um Heap Máximo.
Função Build_Max_Heap(A)
tamanho_heap[A] comprimento[A]
Para i (comprimento[A] 2) decremento 1
faça Max_Heap(A,i)
 Algoritmo Heap-Sort
Função Heap-Sort(A)
Buil Max Heap(A)
Para i comprimento[A] decremento 2
faça trocar A[l] A[i]
tamanho_heap[A] tamanho_heap[A] – 1
Max_Heap(A,1)

14. 20/09/2022
14
Ordenação Por Seleção
 Bibliografia:
 Algoritmos – Teoria e Prática – Thomas H.
Cormen
 Apresentação e notas de aula – Pauloemir –
Profº AED da UFRPE
 Links:
http://www.cin.ufpe.br/~joa
http://www.iti.fh-flensburg.de/lang/algorithmen/sortieren/heap/heapen.htm