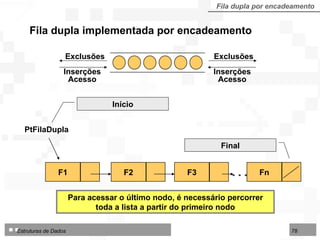
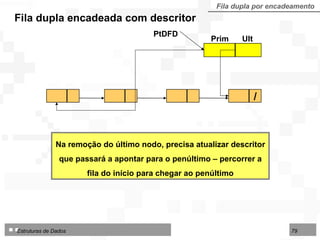
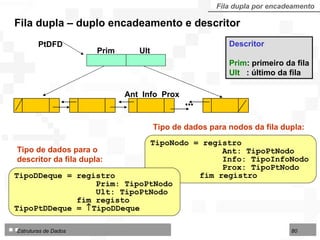
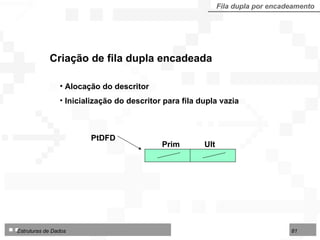
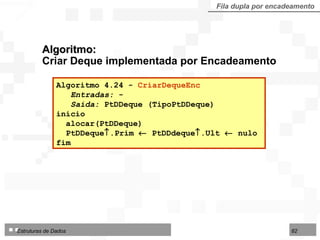
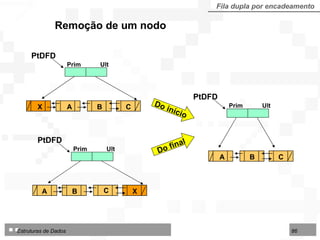
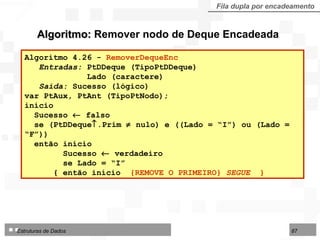
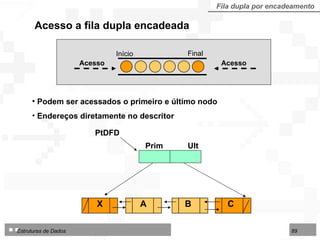
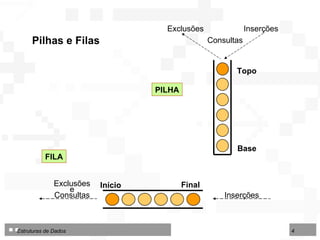
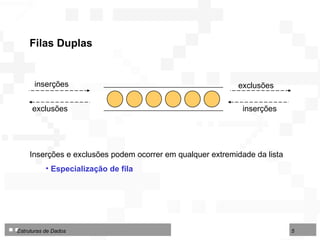
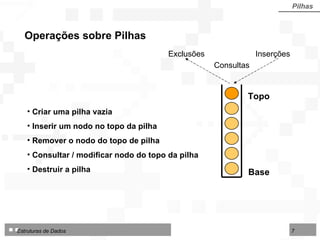
O documento discute pilhas e filas, que são listas lineares especiais com disciplina restrita de organização e acesso aos seus nós. Apresenta as operações básicas de pilhas (LIFO) e filas (FIFO) e duas formas de implementação: por contiguidade física usando arranjos e por encadeamento usando ponteiros.

1. Pilhas e filas Estudo de listas lineares especiais, com disciplina restrita de organização e de acesso a seus nodos

2. Pilhas e filas Disciplina restrita acesso permitido somente em alguns n odo s Com disciplina restrita de organização e acesso a seus nodos Listas lineares especiais

3. Pilha Listas lineares especiais mais usuais Pilhas e filas Fila LIFO Last In First Out o último componente inserido é o primeiro a ser retirado FIFO First In First Out o primeiro componente inserido é também o primeiro a ser retirado

4. Pilhas e Filas Consultas Exclusões Inserções Topo Base Início Final Inserções Exclusões e Consultas PILHA FILA

5. Filas Duplas Inserções e exclusões podem ocorrer em qualquer extremidade da lista Especialização de fila exclusões inserções exclusões inserções

6. Pilhas e filas Pilhas

7. Criar uma pilha vazia Inserir um nodo no topo da pilha Remover o nodo do topo de pilha Consultar / modificar nodo do topo da pilha Destruir a pilha Operações sobre Pilhas Pilhas Consultas Exclusões Inserções Topo Base

8. Pilhas Pilhas implementadas por contiguidade física

9. Pilha - contig u idade física Pilha – contiguidade física Implementada sobre um arranjo Índices de controle da pilha: BASE da pilha TOPO atual da pilha LIMITE máximo que pode ser ocupado pela pilha Lim Topo Base Pilha Índices do arranjo

10. Exemplo de manipulação de uma pilha Retorna “7” 1. Inicializar pilha de valores inteiros, a partir do índice 1, máximo 10 nós 2. Inserir nodo com valor 3 3. Inserir nodo com valor 7 4. Inserir nodo com valor 5 5. Remover nodo do topo 6. Consultar pilha Pilha – contiguidade física LIM TOPO BASE PILHA 10 9 8 7 6 5 4 3 2 1 3 LIM TOPO BASE 10 9 8 7 6 5 4 3 2 1 3 7 LIM TOPO BASE 10 9 8 7 6 5 4 3 2 1 3 7 5 LIM TOPO BASE 10 9 8 7 6 5 4 3 2 1 3 7 LIM TOPO BASE 10 9 8 7 6 5 4 3 2 1 PILHA PILHA PILHA PILHA

11. Pilha – contiguidade física TipoPilha = arranjo [1..N] de TipoNodo Operações Tipo de dados utilizado nos algoritmos para pilha implementada por contiguidade física: Criar uma pilha vazia Inserir um nodo no topo da pilha Remover o nodo do topo de pilha Consultar / modificar nodo do topo da pilha

12. 1. Definir valor do índice de BASE da pilha 2. Definir valor máximo de nodos que a pilha pode ter  LIM 3. Indicar que a pilha está vazia através do valor de TOPO Exemplo: Base  1 Topo  Base – 1 Lim  6 Criação da pilha Pilha – contiguidade física Lim Topo Base Pilha 10 9 8 7 6 5 4 3 2 1

13. Algoritmo 4.1 - InicializarPilhaArr Entrada: Base (inteiro) Saída: Topo (inteiro) início Topo  Base – 1 fim Algoritmo: Inicializar Pilhas implementada sobre Arranjo Pilha – contiguidade física

14. Inserção de um nodo na pilha Pilha – contiguidade física Lim Topo Base Pilha 10 9 8 7 6 5 4 3 2 1 Lim Topo Base Pilha 10 9 8 7 6 5 4 3 2 1 Operação PUSH

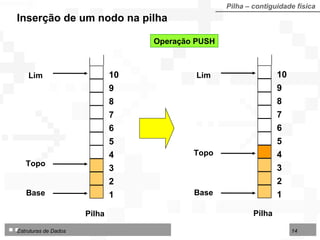
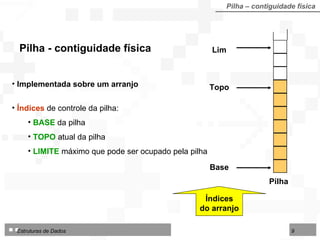
15. Pilha – contiguidade física Algoritmo: Inicializar Pilhas implementada sobre Arranjo Algoritmo 4.2 - InserirPilhaArr Entradas: Pilha (TipoPilha) Lim (inteiro) Topo (inteiro) Valor (TipoNodo) Saídas: Pilha (TipoPilha) Topo (inteiro) Sucesso (lógico) início se Topo < Lim então início Topo  Topo + 1 Pilha[Topo]  Valor Sucesso  verdadeiro fim senão Sucesso  falso fim

16. Pilha – contiguidade física Remoção de um nodo da pilha Lim Topo Base Pilha 10 9 8 7 6 5 4 3 2 1 Lim Topo Base Pilha 10 9 8 7 6 5 4 3 2 1 Operação POP

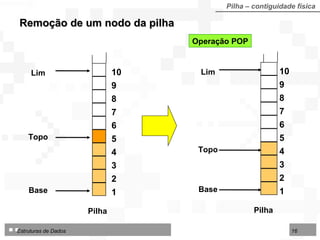
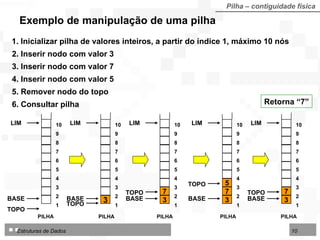
17. Algoritmo 4.3 - RemoverPilhaArr Entradas: Pilha (TipoPilha) Topo (inteiro) Base (inteiro) Saídas: Pilha (TipoPilha) Topo (inteiro) Sucesso (lógico) ValorRemovido (TipoNodo) início se Topo  Base então início ValorRemovido  Pilha[Topo] Topo  Topo - 1 Sucesso  verdadeiro fim senão Sucesso  falso fim Algoritmo: Remover nodo do topo de Pilha implementada sobre Arranjo

18. Pilha – contiguidade física Acesso à pilha Somente ao nodo do topo da pilha Para consulta e/ou modificação ? Lim Topo Base Pilha 10 9 8 7 6 5 4 3 2 1

19. Algoritmo 4.4 - ConsultarPilhaArr Entradas: Pilha (TipoPilha) Base (inteiro) Topo (inteiro) Saídas: Valor (TipoNodo) Sucesso(lógico) início se Topo  Base então início Valor  Pilha[Topo] Sucesso  verdadeiro fim senão Sucesso  falso fim Algoritmo: Consultar nodo do topo de Pilha implementada sobre Arranjo

20. Pilhas Pilhas implementadas por encadeamento

21. Pilha implementada por encadeamento TipoNodo = registro Info: TipoInfo Elo: TipoPtNodo fim registro Tipo de dados utilizado nos algoritmos: Base Topo inserções remoções ? consultas PtPilha Info Elo Topo da pilha Base da pilha Endereço do topo da pilha

22. Pilha por encadeamento Criação de pilha encadeada Pilha criada vazia Atribuir endereço nulo para apontador que contém o endereço do topo da pilha

23. Algoritmo: Criar Pilha Encadeada Pilha por encadeamento Algoritmo 4.5 - CriarPilhaEnc Entradas: - Saída: PtPilha (TipoPtNodo) início PtPilha  nulo fim

24. Inserção de um nodo em pilha encadeada Pilha por encadeamento Novo nodo inserido sempre no topo da pilha Topo Topo PtPilha PtPilha Topo Novo nodo Base Base

25. Algoritmo 4.6 - InserirPilhaEnc Entradas: PtPilha (TipoPtNodo) Valor (TipoInfo) Saída: PtPilha (TipoPtNodo) Variável local: PtNovo (TipoPtNodo) início alocar(PtNovo) PtNovo  .Info  Valor PtNovo  .Elo  PtPilha PtPilha  PtNovo fim Algoritmo: Inserir nodo em Pilha Encadeada Pilha por encadeamento

26. Remo ção de um nodo de uma pilha encadeada Pilha por encadeamento Só pode ser removido o nodo do topo da pilha PtPilha Topo Topo PtPilha Base Base Nodo a ser removido

27. Pilha por encadeamento Algoritmo: Remover nodo de Pilha Encadeada Algoritmo 4.7 - RemoverPilhaEnc Entrada: PtPilha (TipoPtNodo) Saídas: PtPilha (TipoPtNodo) Sucesso (lógico) Variável local: PtAux (TipoPtNodo) início se PtPilha  nulo então início PtAux  PtPilha PtPilha  PtPilha  .Elo liberar(PtAux) Sucesso  verdadeiro fim senão Sucesso  falso fim

28. Acesso à pilha encadeada Pilha por encadeamento Só pode ser acessado o nodo do topo da pilha Topo PtPilha Base Nodo que pode ser acessado

29. Pilha por encadeamento Algoritmo: Consultar nodo do topo de Pilha Encadeada Algoritmo 4.8 - ConsultarPilhaEnc Entrada: PtPilha (TipoPtNodo) Saídas: Valor (TipoInfo) Sucesso (lógico) início se PtPilha = nulo então Sucesso  falso senão início Sucesso  verdadeiro Valor  PtPilha  .Info fim fim

30. Pilha por encadeamento Algoritmo: Desempilhar Consulta nodo do topo da pilha, e o remove da pilha Algoritmo 4.9 - Desempilhar Entrada: PtPilha (TipoPtNodo) Saídas: PtPilha (TipoPtNodo) Valor (TipoInfo) Sucesso (lógico) Variável local: PtAux (TipoPtNodo) início se PtPilha = nulo então Sucesso  falso senão início Sucesso  verdadeiro Valor  PtPilha  .Info PtAux  PtPilha PtPilha  PtPilha  .Elo liberar(PtAux) fim fim

31. Destruição de uma pilha encadeada Pilha por encadeamento Liberar espaço ocupado pelos nodos, sempre a partir do topo da pilha No final: apontador para o topo = endereço nulo PtPilha = nil Base Topo Base Topo Base Topo Base Topo PtPilha PtPilha PtPilha

32. Pilha por encadeamento Algoritmo: Destruir Pilha Encadeada Algoritmo 4.10 - DestruirPilhaEnc Entrada: PtPilha (TipoPtNodo) Saída: PtPilha (TipoPtNodo) Variável local: PtAux (TipoPtNodo) início enquanto PtPilha ≠ nulo faça início PtAux  PtPilha PtPilha  PtPilha  .Elo liberar(PtAux) fim fim

33. Pilhas e filas Filas

34. Filas Operações válidas: Criar uma fila vazia Inserir um nodo no final da fila Excluir o nodo do início da fila Consultar / modificar nodo do início da fila Destruir a fila Filas Inserções Exclusões e Consultas Final Início

35. Filas Filas implementadas por contiguidade física

36. LI : limite inferior da área IF : início da fila FF : final da fila LS : limite superior da área Fila vazia IF = 0 Fila implementada sobre arranjo Fila por contiguidade Inserções Exclusões e Consultas 1 2 3 4 5 6 7 8 9 10 12 13 14 LI LS IF FF FILA

37. Evolução da Fila Fila por contiguidade Inicializar a fila Inserir um novo nodo com valor 3 Inserir um novo nodo com valor 7 Inserir um novo nodo com valor 5 Remover um nodo FILA 1 2 4 3 6 5 1 2 4 3 6 5 FILA LI=IF=FF LS 3 1 2 4 3 6 5 FILA LI=IF LS 3 7 FF 1 2 4 3 6 5 FILA LI=IF LS 3 7 5 FF 1 2 4 3 6 5 FILA LI LS 7 5 FF IF

38. Ocupação circular do arranjo Fila por contiguidade LS FF IF LI FILA 1 2 3 4 5 6 7 8 9 10 12 13 14 1 2 3 4 5 6 7 8 9 10 12 13 14 LS FF IF LI FILA 1 2 3 4 5 6 7 8 9 10 12 13 14 LS FF IF LI FILA 1 2 3 4 5 6 7 8 9 10 12 13 14 LS FF IF LI FILA 1 2 3 4 5 6 7 8 9 10 12 13 14 LS FF IF LI FILA

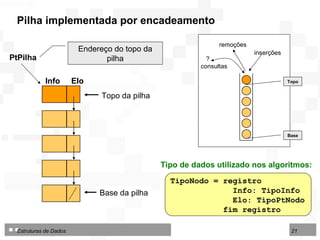
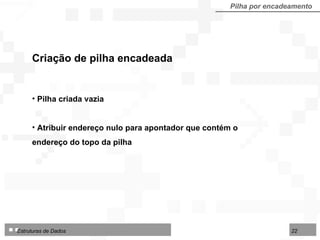
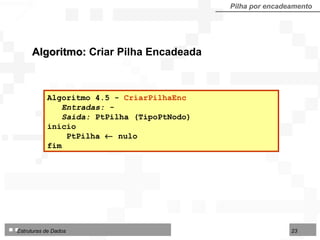
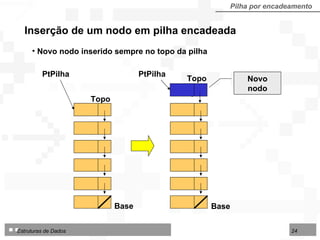
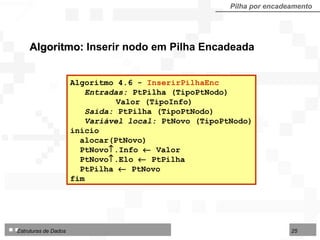
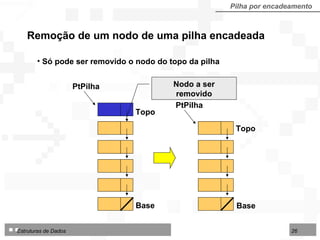
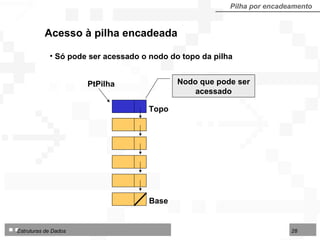
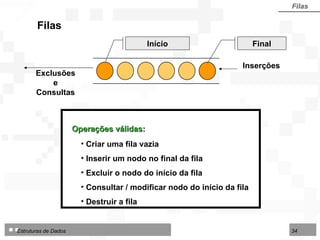
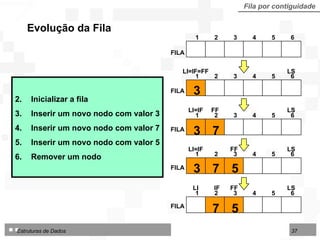
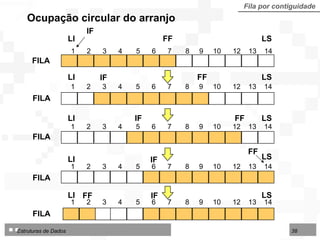
39. Operações sobre Filas implementadas por contiguidade Fila por contiguidade Criar uma fila vazia Inserir um nodo no final da fila Excluir o nodo do início da fila Consultar / modificar nodo do início da fila TipoFila = arranjo [1..N] de TipoNodo Tipo de dados utilizado nos algoritmos para fila implementada por contiguidade física:

40. Criação de uma fila Fila por contiguidade Inicializar variáveis que controlam início e final da fila e início e final da área disponível para a fila ... ... FF IF LI LS Espaço disponível para a fila FILA

41. Algoritmo: Inicializar Fila implementada sobre Arranjo Fila por contiguidade Algoritmo 4.11 - InicializarFilaArr Entrada: LI (inteiro) Saídas: IF, FF (inteiros) início IF  FF  LI – 1 fim

42. Inserção de um nodo em uma fila Fila por contiguidade Nodo inserido sempre no final da fila Testar se tem espaço livre para inserir: ... ... atrás na frente ... ... no meio ... ... LI LI LI LS LS LS IF IF IF FF FF FF

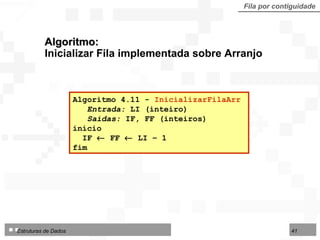
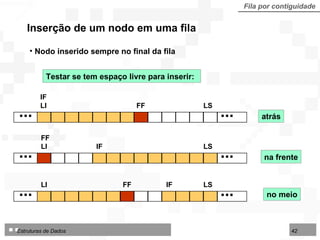
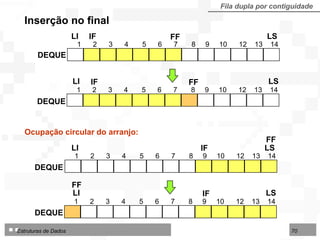
43. Algoritmo: Inserir um nodo em uma Fila implementada sobre Arranjo Algoritmo 4.12 - InserirFilaArr Entradas: Fila (TipoFila) LI, LS, IF, FF (inteiros) Info (TipoNodo) Saídas: IF, FF (inteiros) Sucesso (lógico) início se (FF  IF - 1) e ((IF  LI) ou (FF  LS)) então início se IF = LI - 1 então IF  FF  LI {INSERÇÃO DO PRIMEIRO NODO} senão se FF = L então FF  LI {INSERÇÃO NO INÍCIO} senão FF  FF + 1 {INSERÇÃO NO MEIO OU ATRÁS} FILA[FF]  Info Sucesso  verdadeiro fim senão Sucesso  falso fim

44. Remoção de um nodo de uma fila Fila por contiguidade Nodo removido é sempre o do início da fila 1 2 3 4 5 6 7 8 9 10 12 13 14 LS FF IF LI FILA 1 2 3 4 5 6 7 8 9 10 12 13 14 LS FF IF LI FILA Nodo que pode ser removido

45. Algoritmo: Remover um nodo de uma Fila implementada sobre Arranjo Algoritmo 4.13 - RemoverFilaArr Entradas: LI, LS, IF, FF (inteiros) Saídas: IF, FF (inteiros) Sucesso (lógico) início se IF  LI - 1 então início se IF = FF então IF  FF  LI - 1 {FILA FICA VAZIA} senão se IF = LS então IF  LI senão IF  IF + 1 Sucesso  verdadeiro fim senão Sucesso  falso fim

46. Acesso à fila Fila por contiguidade Só o nodo do início da fila pode ser acessado Acesso para consulta e/ou alteração ? ... ... LS FF IF LI Nodo que pode ser acessado

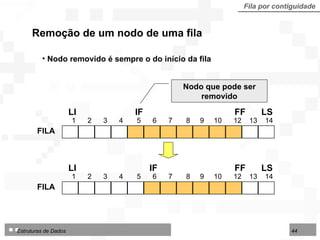
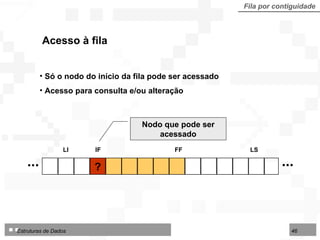
47. Algoritmo: Consultar Fila implementada sobre Arranjo Fila por contiguidade Algoritmo 4.14 - ConsultarFilaArr Entradas: Fila (TipoFila) LI, IF (inteiros) Saídas: Info (TipoNodo) Sucesso (lógico) início se IF  LI - 1 então início Info  Fila[IF] Sucesso  verdadeiro fim senão Sucesso  falso fim

48. Filas Filas implementadas por encadeamento

49. Filas implementadas por encadeamento Filas por encadeamento TipoNodo = registro Info: TipoInfo Elo: TipoPtNodo fim registro Tipo de dados para nodos da fila: Inserções Exclusões e Consultas Final Frente F1 Fn F3 F2 PtFila Endereço do primeiro da fila, para remoção Endereço do final da fila, para inserção Info Elo Para acessar o último nodo, é necessário percorrer toda a fila a partir do primeiro nodo

50. Descritor Prim : primeiro da fila Ult : último da fila Filas por encadeamento com descritor Filas por encadeamento PtDF Prim Ult L1 L2 L4 L3 TipoDFila = registro Prim: TipoPtNodo Ult: TipoPtNodo fim registro TipoPtDFila =  TipoDFila Tipo de dados para o descritor da fila:

51. Operações sobre Filas implementadas por encadeamento com descritor Criar uma fila vazia Inserir um nodo no final da fila Excluir o nodo do início da fila Consultar / modificar nodo do início da fila Destruir a fila Filas por encadeamento

52. Filas por encadeamento Alocar o descritor da fila Descritor inicializado em endereços nulos Fila vazia Criação da fila encadeada PtDF Prim Ult

53. Algoritmo: Criar Fila Encadeada endereçada por descritor Filas por encadeamento Algoritmo 4.15 - CriarFilaEnc Entradas: - Saída: PtDFila (TipoPtDFila) início alocar(PtDFila) PtDFila  .Prim  nulo PtDFila  .Ult  nulo fim

54. Filas por encadeamento Inserção de um nodo na fila encadeada PtDFila Prim Ult / PtDFila Prim Ult PtDFila Prim Ult PtDFila Prim Ult

55. Algoritmo: Inserir novo nodo em Fila Encadeada endereçada por descritor Filas por encadeamento Algoritmo 4.16 - InserirFilaEnc Entradas: PtDFila (TipoPtDFila) Valor (TipoInfo) Saídas: - Variável auxiliar: PtNovo (TipoPtNodo) início alocar(PtNovo) PtNovo  .Info  Valor PtNovo  .Elo  nulo se PtDFila  .Prim = nulo então PtDFila  .Prim  PtNovo senão (PtDFila  .Ult)  .Prox  PtNovo PtDFila  .Ult  PtNovo fim

56. Filas por encadeamento Remoção de um nodo de fila encadeada PtDFila Prim Ult / PtDFila Prim Ult / PtDFila Prim Ult / PtDFila Prim Ult

57. Algoritmo: Remover um nodo de Fila Encadeada endereçada por descritor Filas por encadeamento Algoritmo 4.17 - RemoverFilaEnc Entrada: PtDFila (TipoPtDFila) Saída: Sucesso (lógico) Variável auxiliar: PtAux (TipoPtNodo) início se PtDFila  .Prim  nulo então início PtAux  PtDFila  .Prim PtDFila  .Prim  PtAux  .Elo liberar(PtAux) se PtDFila  .Prim = nulo então PtDFila  .Ult  nulo Sucesso  verdadeiro fim senão Sucesso  falso fim

58. Filas por encadeamento Remoção de um nodo de fila encadeada Só o nodo do início da fila pode ser acessado Acessado diretamente pelo endereço no descritor PtDFila Prim Ult / ?

59. Algoritmo: Consultar Fila Encadeada endereçada por descritor Filas por encadeamento Algoritmo 4.18 - ConsultarFilaEnc Entrada: PtDFila (TipoPtDFila) Saídas: Valor (TipoInfo) Sucesso (lógico) início se PtDFila  .Prim  nulo então início Valor  PtDFila  .Prim  .Info Sucesso  verdadeiro fim senão Sucesso  falso fim

60. Filas por encadeamento Destruição de fila encadeada PtDFila / Prim Ult PtDFila Prim Ult PtDFila = nulo Liberar posições ocupadas pela lista Liberar descritor

61. Algoritmo: Destruir Fila Encadeada endereçada por descritor Filas por encadeamento Algoritmo 4.19 - DestruirFilaEnc Entrada: PtDFila (TipoPtDFila) Saída: PtDFila (TipoPtDFila) Variáveis auxiliares: P1, P2 (TipoPtNodo) início se PtDFila  .Prim  nulo então início P1  PtDFila  .Prim repita P2  P1  .Elo liberar(P1) P1  P2 até P1 = nulo fim liberar(PtDFila) PtDFila  nulo fim

62. Filas Fila dupla - Deque

63. Fila dupla Fila dupla - Deque Inserção, remoção e acesso às duas extremidades Consultas Consultas Início Final Exclusões Inserções Exclusões Inserções

64. Operações válidas: Criar uma fila dupla vazia Inserir um nodo no início Inserir um nodo no fim Excluir um nodo do início Excluir um nodo do fim Consultar / modificar nodo do início ou do fim Destruir a fila dupla Fila dupla Fila dupla - Deque

65. Fila dupla Fila dupla implementada por contiguidade física

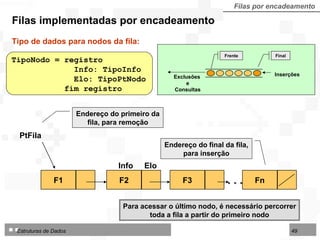
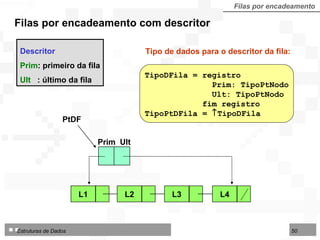
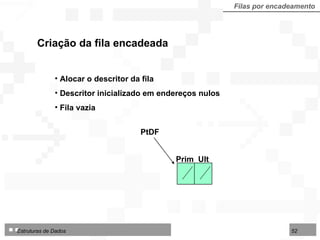
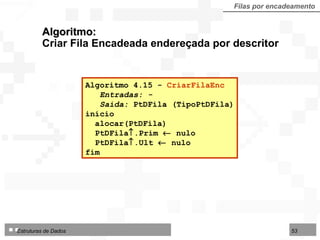
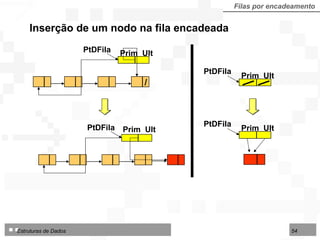
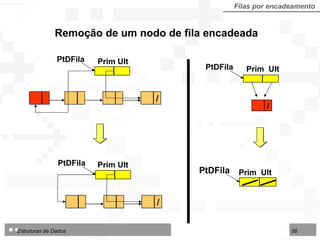
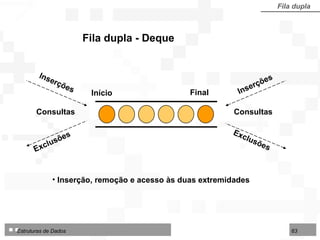
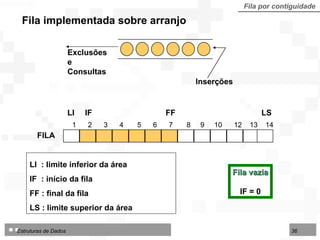
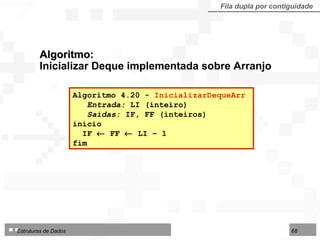
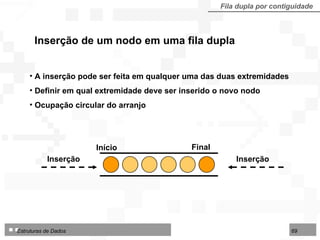
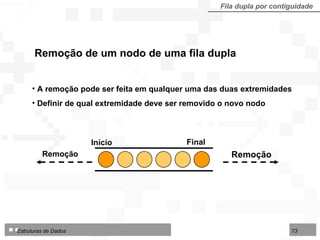
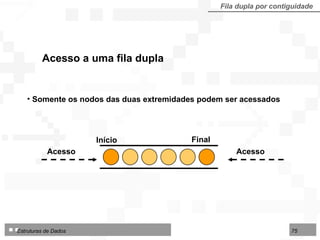
66. LI : limite inferior da área no arranjo IF : início da fila FF : final da fila LS : limite superior da área disponível Fila dupla por contiguidade Fila dupla implementada sobre arranjo TipoFila = arranjo [1..N] de TipoNodo Tipo de dados para fila dupla por contiguidade: 1 2 3 4 5 6 7 8 9 10 12 13 14 LI LS IF FF Deque Consultas Consultas Início Final Exclusões Inserções Exclusões Inserções

67. Criação de uma fila dupla Inicializar indicadores de início e final da fila dupla Fila criada vazia Fila dupla por contiguidade 0 1 2 3 4 5 6 7 8 9 10 12 13 14 LI LS IF FF Deque

68. Algoritmo: Inicializar Deque implementada sobre Arranjo Algoritmo 4.20 - InicializarDequeArr Entrada: LI (inteiro) Saídas: IF, FF (inteiros) início IF  FF  LI – 1 fim Fila dupla por contiguidade

69. Inserção de um nodo em uma fila dupla Fila dupla por contiguidade A inserção pode ser feita em qualquer uma das duas extremidades Definir em qual extremidade deve ser inserido o novo nodo Ocupação circular do arranjo Início Final Inserção Inserção

70. Inserção no final Ocupação circular do arranjo: Fila dupla por contiguidade LS FF LI DEQUE 1 2 3 4 5 6 7 8 9 10 12 13 14 LS FF IF LI 1 2 3 4 5 6 7 8 9 10 12 13 14 IF DEQUE LS FF LI 1 2 3 4 5 6 7 8 9 10 12 13 14 LS FF IF LI 1 2 3 4 5 6 7 8 9 10 12 13 14 IF DEQUE DEQUE

71. Inserção no início Ocupação circular do arranjo: Fila dupla por contiguidade LS FF LI DEQUE 1 2 3 4 5 6 7 8 9 10 12 13 14 LS FF IF LI 1 2 3 4 5 6 7 8 9 10 12 13 14 IF DEQUE LS FF LI 1 2 3 4 5 6 7 8 9 10 12 13 14 LS FF IF LI 1 2 3 4 5 6 7 8 9 10 12 13 14 IF DEQUE DEQUE

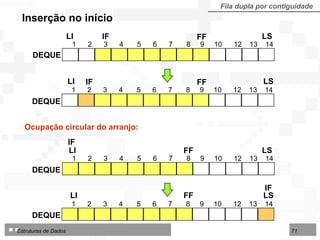
72. Algoritmo: Inserir um nodo no Início de Deque implementada sobre Arranjo Algoritmo 4.21 - InserirIniDequeArr Entrada: Deque (TipoDequeArr) LI, LS, IF, FF (inteiros) Info (TipoNodo) Saídas: Deque (TipoDequeArr) IF, FF (inteiros) Sucesso (lógico) início se ((FF = IF - 1) ou ((IF = LI) e (FF = LS))) então Sucesso  falso senão início Sucesso  verdadeiro se IF = LI – 1 {DEQUE VAZIA} então IF  FF  LI senão se IF > LI então IF  IF – 1 senão IF  LS Deque[IF]  Info fim fim

73. Remoção de um nodo de uma fila dupla Fila dupla por contiguidade A remoção pode ser feita em qualquer uma das duas extremidades Definir de qual extremidade deve ser removido o novo nodo Início Final Remoção Remoção

74. Algoritmo: Remover o nodo do Fim da Deque implementada sobre Arranjo Algoritmo 4.22 - RemoverFimDequeArr Entradas: LI, LS, IF, FF (inteiros) Saídas: IF, FF (inteiros) Sucesso (lógico) início se IF  LI – 1 então início se IF = FF {DEQUE VAI FICAR VAZIA} então IF  FF  LI - 1 senão se FF = LI então FF  LS senão FF  FF - 1 Sucesso  verdadeiro fim senão Sucesso  falso fim

75. Acesso a uma fila dupla Fila dupla por contiguidade Somente os nodos das duas extremidades podem ser acessados Início Final Acesso Acesso

76. Algoritmo: Consultar qual o Maior valor contido nas extremidades de uma Deque implementada sobre Arranjo Algoritmo 4.23 - ConsultarMaiorDequeArr Entradas: Deque (TipoDequeArr) LI, IF, FF (inteiros) Saída: MaiorValor (inteiro) início se IF = LI - 1 então MaiorValor  0 senão se Deque[IF] > Deque[FF] então MaiorValor  Deque[IF] senão MaiorValor  Deque[FF] fim

77. Fila dupla Fila dupla implementada por contiguidade física

78. Fila dupla implementada por encadeamento Fila dupla por encadeamento Para acessar o último nodo, é necessário percorrer toda a lista a partir do primeiro nodo F1 Fn F3 F2 PtFila Dupla Início Final Exclusões Inserções Acesso Exclusões Inserções Acesso

79. Fila dupla encadeada com descritor Fila dupla por encadeamento PtDFD / Prim Ult Na remoção do último nodo, precisa atualizar descritor que passará a apontar para o penúltimo – percorrer a fila do início para chegar ao penúltimo

80. TipoNodo = registro Ant: TipoPtNodo Info: TipoInfoNodo Prox: TipoPtNodo fim registro Tipo de dados para nodos da fila dupla: TipoDDeque = registro Prim: TipoPtNodo Ult: TipoPtNodo fim registo TipoPtDDeque =  TipoDDeque Tipo de dados para o descritor da fila dupla: Descritor Prim : primeiro da fila Ult : último da fila Fila dupla – duplo encadeamento e descritor Fila dupla por encadeamento PtDFD Prim Ult Ant Info Prox

81. Criação de fila dupla encadeada Fila dupla por encadeamento Alocação do descritor Inicialização do descritor para fila dupla vazia PtDFD Prim Ult

82. Algoritmo 4.24 - CriarDequeEnc Entradas: - Saída: PtDDeque (TipoPtDDeque) início alocar(PtDDeque) PtDDeque  .Prim  PtDDdeque  .Ult  nulo fim Algoritmo: Criar Deque implementada por Encadeamento Fila dupla por encadeamento

83. Inserção de um novo nodo Fila dupla por encadeamento PtDFD Prim Ult PtDFD Prim Ult A C A B B N N C PtDFD Prim Ult C A B No início No final

84. Algoritmo: Inserir nodo em Deque Encadeada Algoritmo 4.25 - InserirDequeEnc Entradas: PtDeque (TipoPtDeque) Lado (caractere) Valor (TipoInfoNodo) Saída: Sucesso (lógico) var PtNovo (TipoPtNodo) início Sucesso  falso se (Lado = “I”) ou (Lado = “F”) então início Sucesso  verdadeiro alocar(PtNovo) PtNovo  .Info  Valor se Lado = “I” { então início {INSERE NO INÍCIO} SEGUE } Fila dupla por encadeamento

85. então início {INSERE NO INÍCIO} PtNovo  .Ant  nulo se PtDDeque  .Prim = nulo então início PtDDeque  .Ult  PtNovo PtNovo  .Prox  nulo fim senão início PtNovo  .Prox  PtDDeque  .Prim (PtDDeque  .Prim)  .Ant  PtNovo fim PtDDeque  .Prim  PtNovo fim senão início {INSERE NO FINAL} PtNovo  .Prox  nulo se PtDDeque  .Prim = nulo então início PtNovo  .Ant  nulo PtDDeque  .Prim  PtNovo fim senão início (PtDDeque  .Ult)  .Prox  PtNovo PtNovo  .Ant  PtDDeque  .Ult fim PtDDeque  .Ult  PtNovo fim fim fim Algoritmo (cont): Inserir nodo em Deque Encadeada

86. Remoção de um nodo Fila dupla por encadeamento PtDFD Prim Ult PtDFD Prim Ult A C A B B X X C Do final Do início PtDFD Prim Ult C A B

87. Algoritmo: Remover nodo de Deque Encadeada Fila dupla por encadeamento Algoritmo 4.26 - RemoverDequeEnc Entradas: PtDDeque (TipoPtDDeque) Lado (caractere) Saída: Sucesso (lógico) var PtAux, PtAnt (TipoPtNodo); início Sucesso  falso se (PtDDeque  .Prim  nulo) e ((Lado = “I”) ou (Lado = “F”)) então início Sucesso  verdadeiro se Lado = “I” { então início {REMOVE O PRIMEIRO} SEGUE }

88. então início {REMOVE O PRIMEIRO} PtAux  PtDDeque  .Prim se PtDDeque  .Prim = PtDDeque  .Ult então PtDDeque  .Prim  PtDDeque  .Ult  nulo senão início PtDDeque  .Prim  PtAux  .Prox (PtDDeque  .Prim)  .Ant  nulo fim fim senão início {REMOVE O ÚLTIMO} PtAux  PtDDeque  .Ult se PtDDeque  .Prim = PtDDeque  .Ult então PtDDeque  .Prim  PtDDeque  .Ult  nulo senão início PtDDeque  .Ult  PtAux  .Ant (PtDDeque  .Ult)  .Prox  nulo fim fim liberar(PtAux) fim fim Algoritmo (cont.): Remover nodo de Deque Encadeada

89. Acesso a fila dupla encadeada Fila dupla por encadeamento Início Final Acesso Acesso Podem ser acessados o primeiro e último nodo Endereços diretamente no descritor PtDFD Prim Ult C A B X

90. Algoritmo: Consultar Deque implementada por Encadeamento Fila dupla por encadeamento Algoritmo 4.27 - ConsultarDequeEnc Entradas: PtDDeque (TipoPtDDeque) Lado (caractere) Saídas: Valor (TipoInfoNodo) Sucesso (lógico) início Sucesso  falso se (PtDDeque  .Prim  nulo) e ((Lado = “I”) ou (Lado = “F”)) então início Sucesso  verdadeiro se Lado = “I” então Valor  (PtDDeque  .Prim).Info senão Valor  (PtDDeque  .Ult).Info; fim fim