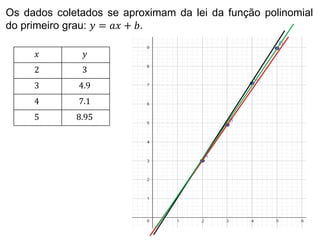
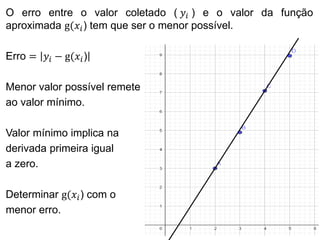
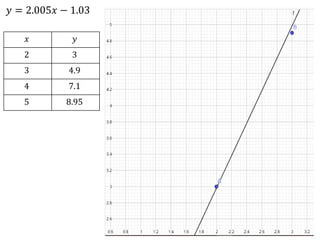
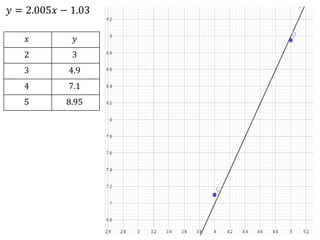
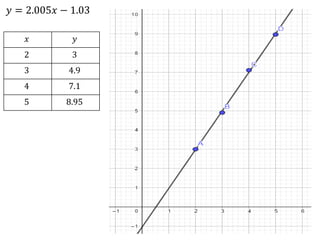
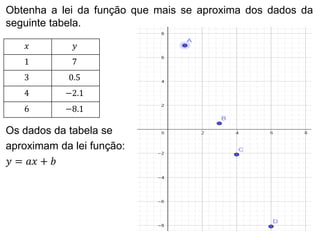
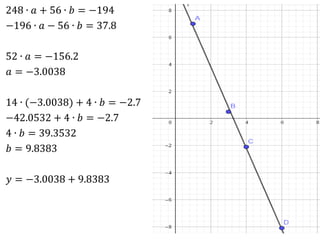
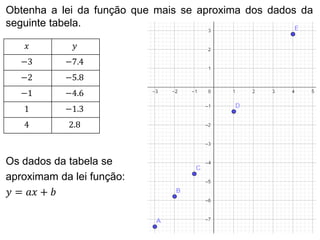
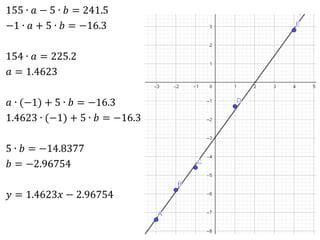
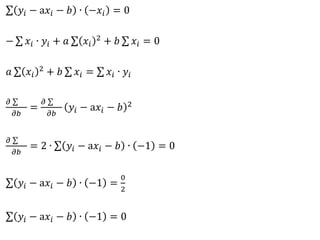O documento apresenta os passos para determinar a função polinomial do primeiro grau que melhor aproxima os dados da tabela. Primeiro, os dados são colocados em uma tabela com as variáveis x e y. Em seguida, os valores de a e b são calculados resolvendo dois sistemas lineares. A função que melhor aproxima os dados é determinada como y = 2.005x - 1.03.

1. Universidade do Extremo Sul Catarinense – UNESC
Engenharia
Disciplina: Cálculo Numérico
Aula 12
Professor: Lucas Sid

2. Durante a realização de um experimento foram coletados
valores que correspondem ao conceito de função. Esses valores
foram expresso na seguinte tabela:
A partir dos dados coletados, qual é a lei da função que melhor
se aproxima desse valores?
Função polinomial do primeiro grau (𝑦 = 𝑎𝑥 + 𝑏).
𝑥 𝑦
2 3
3 4.9
4 7.1
5 8.95

3. Os dados coletados se aproximam da lei da função polinomial
do primeiro grau: 𝑦 = 𝑎𝑥 + 𝑏.
𝑥 𝑦
2 3
3 4.9
4 7.1
5 8.95

4. O erro entre o valor coletado ( 𝑦𝑖 ) e o valor da função
aproximada g(𝑥𝑖) tem que ser o menor possível.
Erro = 𝑦𝑖 − g(𝑥𝑖)
Menor valor possível remete
ao valor mínimo.
Valor mínimo implica na
derivada primeira igual
a zero.
Determinar g(𝑥𝑖) com o
menor erro.

5. Erro = 𝑦𝑖 − g(𝑥𝑖)
𝑛
𝑖=1
Determinar g(𝑥𝑖) com o menor erro significa usar a derivada.
Função modular
Em x = 3 não possui derivada.
𝑦𝑖 − g(𝑥𝑖) 2
𝑛
𝑖=1
Derivada parcial igual a zero.
𝑦𝑖 − a𝑥𝑖 − 𝑏 2
𝑛
𝑖=1

6. Derivada parcial igual a zero.
𝑦𝑖 − a𝑥𝑖 − 𝑏 2
𝑛
𝑖=1
𝜕
𝜕𝑎
= 0
𝜕
𝜕𝑏
= 0 erro mínimo.
𝜕
𝜕𝑎
=
𝜕
𝜕𝑎
𝑦𝑖 − a𝑥𝑖 − 𝑏 2
𝜕
𝜕𝑎
= 2 ∙ 𝑦𝑖 − a𝑥𝑖 − 𝑏 ∙ −𝑥𝑖 = 0
𝑦𝑖 − a𝑥𝑖 − 𝑏 ∙ −𝑥𝑖 =
0
2
𝑦𝑖 − a𝑥𝑖 − 𝑏 ∙ −𝑥𝑖 = 0

7. 𝑦𝑖 − a𝑥𝑖 − 𝑏 ∙ −𝑥𝑖 = 0
− 𝑥𝑖 ∙ 𝑦𝑖 + 𝑎 𝑥𝑖
2 + 𝑏 𝑥𝑖 = 0
𝑎 𝑥𝑖
2 + 𝑏 𝑥𝑖 = 𝑥𝑖 ∙ 𝑦𝑖
𝜕
𝜕𝑏
=
𝜕
𝜕𝑏
𝑦𝑖 − a𝑥𝑖 − 𝑏 2
𝜕
𝜕𝑏
= 2 ∙ 𝑦𝑖 − a𝑥𝑖 − 𝑏 ∙ −1 = 0
𝑦𝑖 − a𝑥𝑖 − 𝑏 ∙ −1 =
0
2
𝑦𝑖 − a𝑥𝑖 − 𝑏 ∙ −1 = 0

8. 𝑦𝑖 − a𝑥𝑖 − 𝑏 ∙ −1 = 0
− 𝑦𝑖 + 𝑎 𝑥𝑖 + 𝑏 = 0
𝑎 𝑥𝑖 + 𝑛 ∙ 𝑏 = 𝑦𝑖
A determinação dos valores de 𝑎 e 𝑏 é obtida por:
𝑎 𝑥𝑖
2
+ 𝑏 𝑥𝑖 = 𝑥𝑖 ∙ 𝑦𝑖
𝑎 𝑥𝑖 + 𝑛 ∙ 𝑏 = 𝑦𝑖

9. A determinação dos valores de 𝑎 e 𝑏 é obtida por:
𝑎 𝑥𝑖
2 + 𝑏 𝑥𝑖 = 𝑥𝑖 ∙ 𝑦𝑖
𝑎 𝑥𝑖 + 𝑛 ∙ 𝑏 = 𝑦𝑖
𝑥 𝑦
2 3
3 4.9
4 7.1
5 8.95
𝑥 𝑦 𝑥 ∙ 𝑦 𝑥2
2 3
3 4.9
4 7.1
5 8.95
𝑥 𝑦 𝑥 ∙ 𝑦 𝑥2
2 3 6 4
3 4.9 14.7 9
4 7.1 28.4 16
5 8.95 44.75 25
14 23.95 93.85 54
𝑥𝑖 𝑦𝑖 𝑥𝑖𝑦𝑖 𝑥𝑖
2

10. A determinação dos valores de 𝑎 e 𝑏 é obtida por:
𝑎 𝑥𝑖
2 + 𝑏 𝑥𝑖 = 𝑥𝑖 ∙ 𝑦𝑖
𝑎 𝑥𝑖 + 𝑛 ∙ 𝑏 = 𝑦𝑖
𝑎 ∙ 54 + 𝑏 ∙ 14 = 93.85
𝑎 ∙ 14 + 4 ∙ 𝑏 = 23.95
𝑥 𝑦 𝑥 ∙ 𝑦 𝑥2
2 3 6 4
3 4.9 14.7 9
4 7.1 28.4 16
5 8.95 44.75 25
14 23.95 93.85 54
𝑥𝑖 𝑦𝑖 𝑥𝑖𝑦𝑖 𝑥𝑖
2

11. 𝑎 ∙ 54 + 𝑏 ∙ 14 = 93.85 ∙ (−4)
𝑎 ∙ 14 + 4 ∙ 𝑏 = 23.95 ∙ 14
−216 ∙ 𝑎 − 56 ∙ 𝑏 = −375.4
196 ∙ 𝑎 + 56 ∙ 𝑏 = 335.5
−20 ∙ 𝑎 = −40.1
𝑎 = 2.005
2.005 ∙ 14 + 4 ∙ 𝑏 = 23.95
4 ∙ 𝑏 = 23.95 − 28.07
𝑏 =
−4.12
4
= −1.03
𝑦 = 2.005𝑥 − 1.03
𝑥 𝑦 𝑥 ∙ 𝑦 𝑥2
2 3 6 4
3 4.9 14.7 9
4 7.1 28.4 16
5 8.95 44.75 25
14 23.95 93.85 54
𝑥𝑖 𝑦𝑖 𝑥𝑖𝑦𝑖 𝑥𝑖
2

12. 𝑦 = 2.005𝑥 − 1.03
𝑥 𝑦
2 3
3 4.9
4 7.1
5 8.95

13. 𝑦 = 2.005𝑥 − 1.03
𝑥 𝑦
2 3
3 4.9
4 7.1
5 8.95

14. 𝑦 = 2.005𝑥 − 1.03
𝑥 𝑦
2 3
3 4.9
4 7.1
5 8.95

15. Obtenha a lei da função que mais se aproxima dos dados da
seguinte tabela.
Os dados da tabela se
aproximam da lei função:
𝑦 = 𝑎𝑥 + 𝑏
𝑥 𝑦
1 7
3 0.5
4 −2.1
6 −8.1

16. A determinação dos valores de 𝑎 e 𝑏 é obtida por:
𝑎 𝑥𝑖
2 + 𝑏 𝑥𝑖 = 𝑥𝑖 ∙ 𝑦𝑖
𝑎 𝑥𝑖 + 𝑛 ∙ 𝑏 = 𝑦𝑖
𝑥 𝑦
1 7
3 0.5
4 −2.1
6 −8.1
𝑥 𝑦 𝑥 ∙ 𝑦 𝑥2
1 7
3 0.5
4 −2.1
6 −8.1

17. A determinação dos valores de 𝑎 e 𝑏 é obtida por:
𝑎 𝑥𝑖
2 + 𝑏 𝑥𝑖 = 𝑥𝑖 ∙ 𝑦𝑖
𝑎 𝑥𝑖 + 𝑛 ∙ 𝑏 = 𝑦𝑖
𝑥 𝑦 𝑥 ∙ 𝑦 𝑥2
1 7 7 1
3 0.5 1.5 9
4 −2.1 −8.4 16
6 −8.1 −48.6 36
14 −2.7 −48.5 62
𝑥𝑖 𝑦𝑖 𝑥𝑖𝑦𝑖 𝑥𝑖
2
𝑥 𝑦 𝑥 ∙ 𝑦 𝑥2
1 7
3 0.5
4 −2.1
6 −8.1

18. A determinação dos valores de 𝑎 e 𝑏 é obtida por:
𝑎 𝑥𝑖
2 + 𝑏 𝑥𝑖 = 𝑥𝑖 ∙ 𝑦𝑖
𝑎 𝑥𝑖 + 𝑛 ∙ 𝑏 = 𝑦𝑖
𝑎 ∙ 62 + 𝑏 ∙ 14 = −48.5
𝑎 ∙ 14 + 4 ∙ 𝑏 = −2.7
𝑎 ∙ 62 + 𝑏 ∙ 14 = −48.5 ∙ (4)
𝑎 ∙ 14 + 4 ∙ 𝑏 = −2.7 ∙ (−14)
248 ∙ 𝑎 + 56 ∙ 𝑏 = −194
−196 ∙ 𝑎 − 56 ∙ 𝑏 = 37.8
𝑥 𝑦 𝑥 ∙ 𝑦 𝑥2
1 7 7 1
3 0.5 1.5 9
4 −2.1 −8.4 16
6 −8.1 −48.6 36
14 −2.7 −48.5 62
𝑥𝑖 𝑦𝑖 𝑥𝑖𝑦𝑖 𝑥𝑖
2

19. 248 ∙ 𝑎 + 56 ∙ 𝑏 = −194
−196 ∙ 𝑎 − 56 ∙ 𝑏 = 37.8
52 ∙ 𝑎 = −156.2
𝑎 = −3.0038
14 ∙ (−3.0038) + 4 ∙ 𝑏 = −2.7
−42.0532 + 4 ∙ 𝑏 = −2.7
4 ∙ 𝑏 = 39.3532
𝑏 = 9.8383
𝑦 = −3.0038 + 9.8383

20. Obtenha a lei da função que mais se aproxima dos dados da
seguinte tabela.
Os dados da tabela se
aproximam da lei função:
𝑦 = 𝑎𝑥 + 𝑏
𝑥 𝑦
−3 −7.4
−2 −5.8
−1 −4.6
1 −1.3
4 2.8

21. Obtenha a lei da função que mais se aproxima dos dados da
seguinte tabela.
𝑥 𝑦 𝑥 ∙ 𝑦 𝑥2
−3 −7.4
−2 −5.8
−1 −4.6
1 −1.3
4 2.8
𝑥 𝑦 𝑥 ∙ 𝑦 𝑥2
−3 −7.4 22.2 9
−2 −5.8 11.6 4
−1 −4.6 4.6 1
1 −1.3 −1.3 1
4 2.8 11.2 16
−1 −16.3 48.3 31
𝑥𝑖 𝑦𝑖 𝑥𝑖𝑦𝑖 𝑥𝑖
2

22. A determinação dos valores de 𝑎 e 𝑏 é obtida por:
𝑎 𝑥𝑖
2 + 𝑏 𝑥𝑖 = 𝑥𝑖 ∙ 𝑦𝑖
𝑎 𝑥𝑖 + 𝑛 ∙ 𝑏 = 𝑦𝑖
𝑎 ∙ 31 + 𝑏 ∙ (−1) = 48.3
𝑎 ∙ (−1) + 5 ∙ 𝑏 = −16.3
𝑎 ∙ 31 + 𝑏 ∙ (−1) = 48.3 ∙ (5)
𝑎 ∙ (−1) + 5 ∙ 𝑏 = −16.3
155 ∙ 𝑎 − 5 ∙ 𝑏 = 241.5
−1 ∙ 𝑎 + 5 ∙ 𝑏 = −16.3
𝑥 𝑦 𝑥 ∙ 𝑦 𝑥2
−3 −7.4 22.2 9
−2 −5.8 11.6 4
−1 −4.6 4.6 1
1 −1.3 −1.3 1
4 2.8 11.2 16
−1 −16.3 48.3 31
𝑥𝑖 𝑦𝑖 𝑥𝑖𝑦𝑖 𝑥𝑖
2

23. A determinação dos valores de 𝑎 e 𝑏 é obtida por:
𝑎 𝑥𝑖
2 + 𝑏 𝑥𝑖 = 𝑥𝑖 ∙ 𝑦𝑖
𝑎 𝑥𝑖 + 𝑛 ∙ 𝑏 = 𝑦𝑖
𝑎 ∙ 31 + 𝑏 ∙ (−1) = 48.3
𝑎 ∙ (−1) + 5 ∙ 𝑏 = −16.3
𝑎 ∙ 31 + 𝑏 ∙ (−1) = 48.3 ∙ (5)
𝑎 ∙ (−1) + 5 ∙ 𝑏 = −16.3
155 ∙ 𝑎 − 5 ∙ 𝑏 = 241.5
−1 ∙ 𝑎 + 5 ∙ 𝑏 = −16.3
𝑥 𝑦 𝑥 ∙ 𝑦 𝑥2
−3 −7.4 22.2 9
−2 −5.8 11.6 4
−1 −4.6 4.6 1
1 −1.3 −1.3 1
4 2.8 11.2 16
−1 −16.3 48.3 31
𝑥𝑖 𝑦𝑖 𝑥𝑖𝑦𝑖 𝑥𝑖
2

24. 155 ∙ 𝑎 − 5 ∙ 𝑏 = 241.5
−1 ∙ 𝑎 + 5 ∙ 𝑏 = −16.3
154 ∙ 𝑎 = 225.2
𝑎 = 1.4623
𝑎 ∙ (−1) + 5 ∙ 𝑏 = −16.3
1.4623 ∙ (−1) + 5 ∙ 𝑏 = −16.3
5 ∙ 𝑏 = −14.8377
𝑏 = −2.96754
𝑦 = 1.4623𝑥 − 2.96754