[1] O documento introduz os conceitos básicos de códigos convolucionais e corretores de erros, incluindo suas classificações, taxas de código, esquemas de codificação e decodificação. [2] É apresentada uma cronologia histórica dos principais desenvolvimentos dos códigos convolucionais, desde 1955 até 1967. [3] São descritos em detalhes códigos convolucionais para correção de erros em salva, definindo suas capacidades, espaço de guarda, interleaving e exemplos de códigos como Berlekamp-




![Os códigos básicos tem relação ( 2 n0 ,2 n0 2n0 ) e matriz "check" de paridade na
2 2
forma:
H [ B0 B1 B2 ... B2 N 0 1 ]
onde Bi é relacionada com Bi-1 da seguinte forma:
0 0 0 ... 0
1 0 0 ... 0
0 1 0 ... 0
Bi Bi1
0 0 1 ... 0
0
0 0 0 1 0
Para este código ter b2 = n0, nenhuma palavra diferente de zero pode ter todos os
seus 1's confinados ao bloco 0 e outro bloco qualquer. Uma palavra deste tipo pode ser
representada por:
E = E0 0 0 0 ... Ei 0 0 ... 0
onde E0 é diferente de zero.
Se B0 pode ser escolhido de maneira que EHt seja não-zero para todos os valores
de E0 0, Ei e i, então o código terá b2 = n0.
Para que isto ocorra, devemos ter:
E0 Ei [B0 Bi]t 0 ; 1 i 2n0 1
Para n0 i 2n0 1 , o quadrante superior direito de [B0 Bi] é a matriz de zeros
de ordem n0. Assim, escolhemos a metade superior de B0 não-singular para a equação
acima valer. Para simplificação da decodificação escolhemos esta como a matriz
identidade, chamada de In0.
Para 1 i n0 1 , as matrizes [B0 Bi] devem ser simultaneamente não-singulares
para a equação acima valer. Procedimentos matriciais elementares reduzem esta matriz a:
I n0 Xi
0 Yi
5](https://image.slidesharecdn.com/artigo-codigosconvolucionaissequenciais-120320114707-phpapp01/85/Codigos-Convolucionais-sequenciais-5-320.jpg)
![Nesta forma, [B0 Bi] só será não-singular se, e somente se, Yi for não-singular. Já
existem matrizes Yi calculadas para vários valores de n0.
Note que, códigos deste tipo necessitam que o bit de paridade seja transmitido
antes dos bits de informação do bloco.
Os códigos com k0 = n0 - 1 construídos segundo acima chegam ao limite de b2.
Códigos com k0 < n0 - 1 podem ser construídos da mesma forma ou segundo um artifício:
fazendo "interleave" de bloco de dois códigos com capacidades b1 e b2 ,de forma a termos
um terceiro código com n03 = n01 + n02, k03 = k01 + k02 e m3 = max(m1,m2). Este artifício
constrói códigos onde nem k0, nem n0 - k0 sejam 1.
A decodificação de códigos BPM funciona da seguinte maneira: assuma uma salva
no 0-ésimo bloco, os primeiros n0 bits da síndrome serão iguais ao padrão de erro
adicionado ao bloco, por que a metade superior da matriz é a matriz identidade de ordem
n0. A segunda parte da síndrome deverá ser:
s2 = E0 [ B02 ]t
onde s2 é a segunda metade da síndrome, E0 é a salva e B02 é a metade inferior de B0.
Já que s1 é idêntica a E0, se for verdade:
s2 + s1 [ B02 ]t = 0
então a salva ocorreu no 0-ésimo bloco.
Procedendo "Interleave" sobre um código BPM básico, chega-se aos seguintes
parâmetros:
m = (2n0 - 1)i + 1
n = mn0 = (2n0 - 1)n0i + n0
k = mk0
b2 = in0
b = b2 - (n0 - 1) = n0(i - 1) + 1
6](https://image.slidesharecdn.com/artigo-codigosconvolucionaissequenciais-120320114707-phpapp01/85/Codigos-Convolucionais-sequenciais-6-320.jpg)


![n 0 ( n0 1)
m ( 2n0 1)i
2
k0 n0 1
b in 0
g n 1
O espaço de guarda será o mesmo que o caso sem "interleave": n - 1.
Códigos de Baixa Taxa
Os melhores códigos corretores de salvas com taxas baixas possuem os seguintes
parâmetros:
m3
n n0 m 3n0
n 1 n 1
b[ ] n0 [ 0 ]
2 2
k0 1
g n 1
A matriz B0 para estes códigos tem a forma:
a I n 0 1
B0 b On0 1
c On0 1
onde a é a coluna nula de tamanho n0 - 1, b é a coluna de tamanho n0 - 1 formada por
zeros e um único 1 na posição n0 / 2 e c é formada de zeros exceto na posição n0 - 1.
A decodificação é direta: se ocorrer uma salva de comprimento b ou menor, os
dois "check" do bit de informação do primeiro bloco estarão errados. Caso contrário, um
dos, ou ambos estarão corretos. Se o bit de informação do segundo bloco estiver em erro,
10](https://image.slidesharecdn.com/artigo-codigosconvolucionaissequenciais-120320114707-phpapp01/85/Codigos-Convolucionais-sequenciais-10-320.jpg)
![ele será corrigido da mesma maneira depois que o primeiro bloco for deslocado para fora
do decodificador.
Se procedermos "Interleaving" nos códigos mostrados teremos:
m 2i 1
n n0 m
n 1 n 1
b[ ] in0 [ 0 ]
2 2
k0 1
g n 1
para qualquer escolha de n0 e i.
Códigos Para Correção de Erros em Salvas e Erros Aleatórios
Estes códigos visam a correção de erros não restritos a uma salva somente. As
técnicas utilizadas podem ser divididas em:
1. Proceder "interleaving" sobre um código corretor de erros de pequeno
comprimento.
2. Construir um código com certa capacidade de correção de erros em salva e
de erros randômicos.
3. decodificação "adaptativa", onde o decodificador tenta determinar o tipo
de erro que ocorreu e tenta corrigi-lo.
"Interleave" de blocos com grau i sobre um código convolucional com capacidade
t de correção de erros randômicos produz um código convolucional mais longo com
capacidade de corrigir salvas de comprimento até [t/n0]i além dos erros randômicos.
Um exemplo de código "misto" que combina ambas as capacidades são os códigos
auto-ortogonais difusos. Estes estão no meio termo entre os extremos dos códigos auto-
ortogonais que possuem capacidade de correção de erros randômicos t, porém com
capacidade de correção de salvas pouco maior que t; e os códigos Idaware que
apresentam grande capacidade de correção de salvas porém com t = 1.
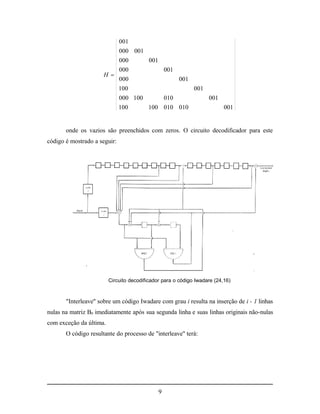
11](https://image.slidesharecdn.com/artigo-codigosconvolucionaissequenciais-120320114707-phpapp01/85/Codigos-Convolucionais-sequenciais-11-320.jpg)
