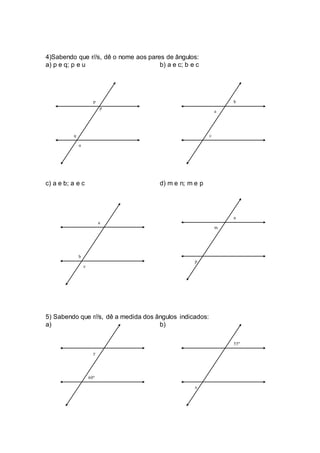
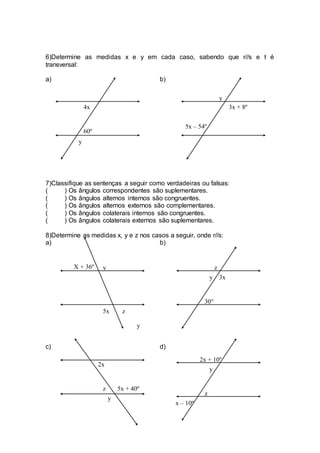
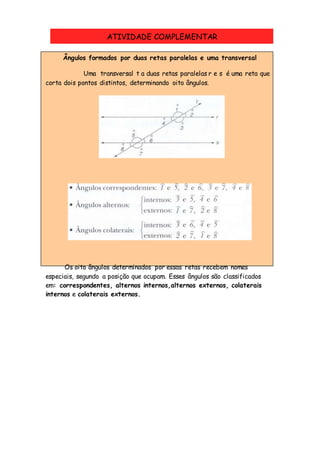
1) O documento fornece uma lista de exercícios sobre ângulos correspondentes e alternos formados por duas retas paralelas cortadas por uma transversal. 2) Inclui definições e nomes dos diferentes tipos de ângulos formados - correspondentes, alternos internos, externos, colaterais internos e externos. 3) A atividade complementar apresenta exercícios adicionais para identificar medidas de ângulos nessas situações.

1. Lista de exercícios: ângulos correspondentes e alternos
1)Sabendo que r//s, dê a medida dos ângulos indicados:
a) b)
2)Nas figuras a seguir r//s e t é transversal, determine as medidas x e y dos
ângulos destacados:
a) b)
3)Sabendo que r//s, calcule, em cada caso, o valor de x:
a) b)
40º
x
120º
z
120º
xy
x 70º
y
X + 15º
40º
7x + 70º
4
3x + 20º

2. 4)Sabendo que r//s, dê o nome aos pares de ângulos:
a) p e q; p e u b) a e c; b e c
c) a e b; a e c d) m e n; m e p
5) Sabendo que r//s, dê a medida dos ângulos indicados:
a) b)
p
q
u
b
a
c
p
a
b
c
n
m
p
y
60º
55º
x

3. 6)Determine as medidas x e y em cada caso, sabendo que r//s e t é
transversal:
a) b)
7)Classifique as sentenças a seguir como verdadeiras ou falsas:
( ) Os ângulos correspondentes são suplementares.
( ) Os ângulos alternos internos são congruentes.
( ) Os ângulos alternos externos são complementares.
( ) Os ângulos colaterais internos são congruentes.
( ) Os ângulos colaterais externos são suplementares.
8)Determine as medidas x, y e z nos casos a seguir, onde r//s:
a) b)
c) d)
4x
60º
y
3x + 8º
5x – 54º
y
X + 36º y
z5x
y
z
3x
30°
y
2x
5x + 40ºz
y
2x + 10º
y
x – 10º
z

4. Ângulos formados por duas retas paralelas e uma transversal
Uma transversal t a duas retas paralelas r e s é uma reta que
corta dois pontos distintos, determinando oito ângulos.
Os oito ângulos determinados por essas retas recebem nomes
especiais, segundo a posição que ocupam. Esses ângulos são classificados
em: correspondentes, alternos internos,alternos externos, colaterais
internos e colaterais externos.
ATIVIDADE COMPLEMENTAR

5. Ângulos Opostos pelo Vértice
1) Nas figuras seguintes as retas r, s e t são paralelas. Nessas condições
determine os valores dos ângulos a, b, x , y e z .
a) b)
* z + 25º + 50º = 180º 3x + 40 = 5x – 16
(Correspondentes)
z = 180 - 75º 3x - 5x = - 40 - 16
z = 105º - 2x = - 56
x = 28º
y = 50º ( Correspondente)
a = 3x + 40
x = 50º (OPV) a = 3 . 28 + 40
a = 84 + 40
a = 124º
b = 180º - 124
b = 56º

6. 2) Duas retas paralelas, cortadas por uma transversal, determinam dois
ângulos colaterais internos em que a medida de um deles é o triplo da
medida do outro. Faça uma figura representativa dessa situação e
determine as medidas dos oito ângulos formados entre as paralelas e a
transversal.
x + 3x = 180
4x = 180
x = 45º
4 ângulos de 45º e 4 ângulos de 135º
6)Determine as medidas de x e y, em grau, para cada caso. Considere r //
s.
y = 40º (OPV)
x = 45 (correspondentes)
y = 50º + 38º
y = 88º
X
3x
40º
45º
x = 180º -
50º
x = 130º
50º
38º
70º
30º
50º
50º
x +
16°
3x –
10º

7. x= 50º x + 16 + 3x – 10 = 110 y
= x + 16º
4x = 110 – 6 y
= 26º + 16º
Y = 180º - 50º 4x = 104 y
= 42º
Y = 130º x = 26º
7) Na figura, r e s são retas paralelas, e t e u são retas transversais. Determine o valor
dos ângulos a, b, c e d
B =
40º
8) Duas retas paralelas cortadas por uma transversal determinam dois
ângulos alternos externos cujas medidas são º15
2
3

x
e 135º. Qual é o
valor de x ?
º15
2
3

x
= 135º
3x + 30 = 270 ( foi feita a equivalência)
3x = 270 – 30
3x = 240
X = 80º
9) (CARLOS CHAGAS-SP) Na figura abaixo tem-se r//s; t e u são transversais. O
valor de x + y é:
a) 100°
b) 120°
c) 130°
d) 140°
e) 150°
d = 140º
(Colaterais)
b = 180º - 110ª=
70º
a = 180º – 110º=
70º

8. 10) (UF-ES) Uma transversal intercepta duas paralelas formando ângulos alternos
internos expressos em graus por (5x + 8) e (7x – 12). A soma das medidas desses
ângulos é:
a) 40° b) 58° c) 80° d) 116° e) 150°