Apresentação sem net aula-6-3-2012

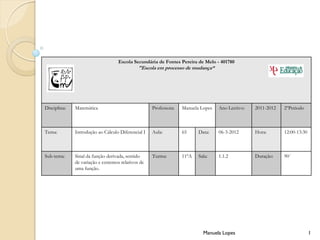
Escola Secundária de Fontes Pereira de Melo - 401780
"Escola em processo de mudança“

Disciplina: Matemática Professora: Manuela Lopes Ano Lectivo: 2011-2012 2ºPeriodo

Tema: Introdução ao Cálculo Diferencial I Aula: 65 Data: 06-3-2012 Hora: 12:00-13:30

Sub-tema: Sinal da função derivada, sentido Turma: 11ºA Sala: 1.1.2 Duração: 90´
de variação e extremos relativos de
uma função.

Manuela Lopes 1


Lição nº 65 Data: 06-3-2012

Sumário:
Sinal da derivada e sentido de
variação.
Resolução da tarefa 19 do
manual escolar e de uma ficha
de trabalho.
Manuela Lopes 2


O conceito de derivada teve a sua
génese a partir da resolução de
problemas ligados à determinação de
velocidades, tangentes, máximos e
mínimos, taxas de variação, que tem
aplicações práticas nos mais diversos
campos, como mecânica, engenharia,
física, biologia e economia.
A derivada é uma ferramenta
poderosa para o estudo e análise de
funções.

Manuela Lopes 3


Hoje vamos aprender a relacionar o sinal da derivada de
uma função num intervalo ]a, b[, com o crescimento ou
decrescimento da função no referido intervalo.

Manuela Lopes 4


Objectivos:
Relacionar monotonia de uma função e o sinal da sua
derivada;
Estudar a monotonia de uma função;
Analisar o sentido de variação de uma função;
Associar o sinal da derivada ao sentido de variação de
uma função;
Utilizar o quadro de sinal.

Manuela Lopes 5


Manuela Lopes 6


 Desenvolvimento da escola virtual

Manuela Lopes 7



Manuela Lopes 8



Manuela Lopes 9



Manuela Lopes 10



Manuela Lopes 11



Manuela Lopes 12


 Relação entre uma função e o sinal da sua
derivada

Manuela Lopes 13


Estratégia para o estudo da derivada e o
sentido de variação de uma função

 1º Determina-se a derivada da função dada.
 2º Calcula-se os zeros da derivada.
 3º Constrói-se um quadro de sinal onde se
estuda o sinal da derivada.
 4º No mesmo quadro de sinal estuda-se o
sentido de variação da função.
 5º Apresenta-se o estudo final em forma de
intervalo.
Manuela Lopes 14


 Exemplos 1
 No referencial da figura
está representada a
função g.
 A partir da observação do
gráfico da função g,
completa a seguinte tabela
de sinal da derivada de g,
com os sinais + ou - .

Manuela Lopes 15


 Exemplos 1

 Podemos concluir que:
 A função g é estritamente crescente nos
intervalos ]-, -2[ e ]-1, 1[ e ] 2, +[
 A função g é estritamente decrescente no
intervalo ]-2,-1] e ]1, 2[
Manuela Lopes 16


 Exemplos 2

 Estude a variação da seguinte
função cúbica

g ( x)  x  3 x  1
3

Manuela Lopes 17


 Exemplos 2

x - -1 1 +
Conclusão:
g(x) é estritamente crescente
g´(x) + 0 - 0 +
em ]-, -1[ e ]1, +[
g(x)
g(x) é estritamente
decrescente em ]- 1,1 [
Manuela Lopes 18


 Exemplos 2
Relacionando o gráfico da função f, a vermelho,
com o gráfico da sua derivada f´, a verde, verifica-
se a conclusão anterior.

g(x) é estritamente crescente em ]-, -1[ e ]1, +[
g(x) é estritamente decrescente em ]- 1,1 [
Manuela Lopes 19


 Praticar os conceitos

Tarefa 19 – página 82
Ficha de trabalho

Manuela Lopes 20


Síntese aula

Se uma função admite
derivada positiva em
todos os pontos de um
intervalo ] a, b [, então
a função é estritamente
crescente nesse
intervalo.

Manuela Lopes 21


Síntese aula

Se uma função admite
derivada negativa em
todos os pontos de um
intervalo ] a,b [, então a
função é estritamente
decrescente nesse
intervalo.

Manuela Lopes 22


Síntese aula

Se uma função tem
derivada nula em
todos os pontos de
um intervalo ] a,b [,
então a função é
constante nesse
intervalo.

Manuela Lopes 23


Objectivos:
Determinar os extremos relativos de uma
função usando a derivada;
Dar exemplos de funções que não têm
derivada num ponto mas tem extremos nesse
ponto.

Manuela Lopes 24

Apresentação sem net aula-6-3-2012

Mais conteúdo relacionado

Destaque

Semelhante a Apresentação sem net aula-6-3-2012

Apresentação sem net aula-6-3-2012