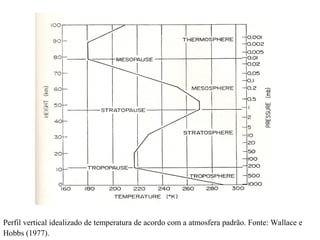
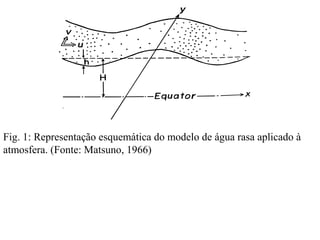
O documento apresenta um mini-curso sobre dinâmica atmosférica. Introduz o modelo de água rasa para descrever os movimentos de grande escala na atmosfera, considerando a aproximação hidrostática e a rotação da Terra. Deriva as equações do modelo a partir das equações de Navier-Stokes para um fluido homogêneo sobre um planeta em rotação. Discute a inclusão de termos convectivos e dissipativos nas equações.

1. XXIV Jornada de Física Teórica
MINI-CURSO:
Tópicos Especiais de Dinâmica da Atmosfera
Professor:
Carlos Frederico Mendonça Raupp (IFT-UNESP)
E-mail: raupp@ift.unesp.br

2. Introdução
 Atmosfera: constitui um invólucro fluido em torno do planeta que está
em incessante movimento devido, em última instância, ao aquecimento
diferenciado pelo sol sobre a Terra;
 Escoamento atmosférico: caracterizado por movimentos que
estendem-se desde escalas milimétricas até às escalas comparáveis com
o próprio tamanho do planeta ⇒ movimentos de escala planetária;
 Fluidos geofísicos: escoamento é significativamente afetado pela
rotação do planeta;
 Movimentos na atmosfera: devem ser descritos por um conjunto
acoplado de equações que representam as leis da hidrodinâmica e da
termodinâmica; ⇒ Hipótese do Contínuo

3. Perfil vertical idealizado de temperatura de acordo com a atmosfera padrão. Fonte: Wallace e
Hobbs (1977).

4. MODELO DE ÁGUA-RASA COM ROTAÇÃO
 Para os movimentos de grande-escala na atmosfera tem-se que L >>
H, sendo L a escala típica de comprimento horizontal dos movimentos e
H a escala de altura típica da troposfera;
 Para esses movimentos, em primeira aproximação, a equação da

continuidade pode ser escrita como div( v ) = 0 , enquanto a equação do
movimento vertical pode ser aproximada pelo balanço hidrostático;
 Dessa forma, vários “ingredientes dinâmicos” desses movimentos
podem ser descritos por um modelo de uma camada de fluido
homogêneo e hidrostático ⇒ modelo de água-rasa;

5. Equações de Navier-Stokes para uma camada de fluido homogêneo
(densidade constante), hidrostático e sobre a Terra em rotação:
∂u ∂u ∂u ∂u 1 ∂p (1a)
+u +v +w − fv = −
∂t ∂x ∂y ∂z ρ ∂x
∂v ∂v ∂v ∂v 1 ∂p (1b)
+u +v +w + fu = −
∂t ∂x ∂y ∂z ρ ∂y
∂p
= ρ
−g (1c)
∂z
∂u ∂v ∂w (1d)
+ + =0
∂x ∂y ∂z
Onde V = (u, v, w)T ⇒ vetor velocidade
p ⇒ pressão hidrostática; ρ ⇒ densidade (constante)
g ⇒ aceleração efetiva da gravidade e f ⇒ parâmetro de Coriolis

6. Fig. 1: Representação esquemática do modelo de água rasa aplicado à
atmosfera. (Fonte: Matsuno, 1966)

7. Se ρ = const (fluido homogêneo, tomando a derivada em x ou em y
da equação hidrostática, tem-se que:
∂∂ p ∂ ∂p
=0 =0 (1.2)
∂ ∂
z x ∂ ∂
z y
Logo, u e v também não dependem de z.
H +h H +h
∂w  ∂u ∂v   ∂u ∂v 
∫
0
∂z
dz = − ∫
0


+ dz ⇒ w( x, y, z = H + h, t ) − w( x, y,0, t ) = −
 ∂x ∂y 

 ∂x + ∂y ( H + h)



(1.3)
Condições de fronteira: (i) w(x,y,0,t) = 0 (sem topografia)
dh ∂ h ∂ h ∂h
(ii) w( z = h +H ) = dt = ∂ +u ∂ +v ∂
t x y
∂h ∂h ∂h  ∂u ∂v   ∂u ∂v 
+u +v +H  ∂x + ∂y  + h ∂x + ∂y  = 0
   (1.4)
∂t ∂x ∂y    

8. Integrando a equação hidrostática em uma coluna de altura ∆h, tem-se:
∂p ∆p ∆ h lim ∆x → 0 ∂p ∂h
= ρ
−g ∆p = ρg∆h → ÷ ∆x
= ρg   → = ρg
∂z ∆x ∆x ∂x ∂x
∆p ∆h lim ∆y →0 ∂p ∂h
∆p = ρg∆h → ÷ ∆y
= ρg  → = ρg
∆y ∆y ∂y ∂y
(1.5a,b)
Substituindo nas equações (1.a,b), obtém-se:
∂u ∂ u ∂ u ∂φ
+u +v − fv + =0 (1.6a)
∂t ∂x ∂y ∂x
∂v ∂v ∂v ∂φ (1.6b)
+u +v + fu + =0
∂t ∂x ∂y ∂y
∂φ ∂φ ∂φ 2  ∂u ∂v   ∂u ∂v 
+ u + v + c  +  + φ +  = 0
 ∂x ∂y   ∂x ∂y  (1.6c)
∂t ∂x ∂y    
φ = gh ⇒ perturbação do geopotencial
c= gH Velocidade das ondas de gravidade puras

9. Simular o efeito da convecção térmica ⇒ inclusão de uma fonte de
massa Fφ na equação da continuidade (1.6c) ⇒ pode também representar
o efeito do aquecimento associado à liberação de calor latente na
atmosfera:
∂u ∂φ  ∂u ∂u 
∂t
− fv +
∂x  ∂x + v ∂y  −κu
= −u  (1.7a)
 
∂v ∂φ  ∂v ∂v 
∂t
+ fu +
∂y  ∂x + v ∂y  −κv
= −u  (1.7b)
 
∂φ 2  ∂u ∂v   ∂φ ∂φ   ∂u ∂v 
+c  + =
 ∂x ∂y  −  u + v  − φ  +  + Fφ − κφ
 ∂x (1.7c)
∂t    ∂y   ∂x ∂y 
  
onde κ é o coeficiente de dissipação do tipo “Rayleigh” e de
resfriamento Newtoniano

10. Linearizando em relação a um estado básico em repouso:
∂u ∂ φ
− fv + κ
=− u (1.8a)
∂t ∂x
∂v ∂φ
+ fu + κ
=− v (1.8b)
∂t ∂y
∂φ ∂u ∂ 
v
+c 2 
∂ +  =Fφ − φ
 κ (1.8c)
∂t  x ∂ 
y
onde κ é o coeficiente de dissipação do tipo “Rayleigh” e de
resfriamento Newtoniano

11. DERIVAÇÃO DO MODELO DE ÁGUA RASA VIA SOLUÇÃO
DO MODELO DE EQUAÇÕES PRIMITIVAS POR SEPARAÇÃO
DE VARIÁVEIS
Modelo de equações primitivas linearizado em relação a um estado
básico em repouso usando a pressão como coordenada vertical:
∂u
−fv +
∂φ=
∂t ∂x
0 (1.9a)
∂v ∂ φ
+ fu + =0 (1.9b)
∂t ∂y
∂u ∂v ∂ω (1.9c)
+ + =0
∂x ∂y ∂p
∂  ∂φ  R J
 ∂p  + σω = − P C
 (1.9d)
∂t  
 p

12. Onde: φ ⇒ geopotencial
ω ⇒ velocidade vertical em coordenada-p
J ⇒ termo de aquecimento/resfriamento diabático
R ⇒ constante dos gases para o ar seco
Cp ⇒ calor específico a pressão constante
R  RT dT 
σ=  −  ⇒ Parâmetro de estabilidade estática do estado
p  pC p dp 
  básico
T = T (p) ⇒ temperatura do estado básico

13. Fazendo 1/ σ ∂ / ∂p (1.9d), obtém-se:
∂ ∂  1 ∂φ   ∂u ∂v  R ∂ J 

 σ ∂p  −  ∂x + ∂y  = − C ∂p  p 
     (1.10)
∂t ∂p     p  
Supor inicialmente o caso adiabático, i.e., J ≡ 0 (analisar os modos
normais do sistema):
∂u ∂ φ
− fv + =0 (1.11a)
∂t ∂x
∂v ∂ φ (1.11b)
+ fu + =0
∂t ∂y
φ
∂ ∂  1 ∂  ∂ u ∂ 
v (1.11c)
  −
σ ∂   ∂ +  =0
∂ ∂ 
t p p  x ∂ 
y

14. Fazendo a seguinte separação de variáveis:
 u   u ( x, y , t ) 
ˆ
   
 v  =  v(x, y, t) G ( p )
ˆ (1.12)
φ  φ( x, y , t ) 
ˆ
   
∂

ˆ
u ∂ˆ 
φ (1.13a)
 ∂ − fv + ∂  =0
ˆ G
 t x
∂

ˆ
v φ
∂ˆ  (1.13b)
∂ + fu +
ˆ
 =0
G
 t ∂ 
y
∂ ˆ d  1 dG   ∂ˆ
φ u ∂ˆ 
v

σ dp  − ∂ + ∂ G = 0 (1.13c)
  x
∂ dp 
t   y

15. De (1.13c), segue que:
∂φˆ
∂t G
= = −c 2 (1.14)
 ∂u ∂v 
ˆ ˆ d  1 dG 

 ∂x + ∂y  dp  σ dp 
  
   
c ⇒ constante de separação (tem dimensão de velocidade)
Logo, a estrutura horizontal é governada por:
∂uˆ
−fv + ˆ
∂ φ=
ˆ
0 (1.15a)
∂ t ∂ x
∂ˆ
v
+fu +
ˆ
∂φ=
ˆ
0 (1.15b)
∂t ∂y
ˆ
∂φ 2  ∂ˆ
u ∂v 
ˆ
+c  ∂x + ∂y  = 0
 (1.15c)
∂t  

16. Equação da Estrutura Vertical
De (1.14) segue que a estrutura vertical é governada pela seguinte
equação:
d  1 dG  1

 σ dp  + c 2 G = 0
 (1.16)
dp  
Supondo como condições de fronteira para o sistema (1.9) ω = 0 em p =
0 (topo)e em p = p0 (superfície), tais condições são escritas como:
dG / dp = 0 em p = 0 (1.17a)
dG / dp = 0 em p = p0 (1.17b)
A eq. (1.16) com as condições de fronteira (1.17a,b) constitui um
problema de Sturm-Liouville.

17. Supondo ainda que σ é constante com a pressão, tem-se que (1.16) torna-
se:
d 2G σ
2
+ 2
G=0
dp c
Equação Característica:
σ
λ2 + 2 = 0 (1.18)
c
σ
λ =± i (1.19)
c
Solução Geral:
σ σ
ip − ip
G ( p ) =Ae c
+Be c (1.20)

18. Aplicando a condição de fronteira (1.17a) em p = 0, tem-se que A = B.
Aplicando a condição de fronteira (1.17b) em p = p0, tem-se:
σ 

i
σ
p0 −i
σ
p0 
 =0
i e c
−e c
c  
 
 σ  σ

sin p0  = 0 ou p 0 = mπ (1.21)

 c  c
m = 0, 1, 2, 3, ...
Logo:
cm = p0
σ
(1.22) Autovalores
mπ
 σ 
G m ( p ) = cos
c p  (1.23)
 Autofunções
 m 

19. Tabela .11: Autovalores cm da equação da estrutura vertical (1.16) com
as condições de fronteira (1.17a,b) para p0 = 1000hPa e σ = 1,6 x 10-6 m4
s2 Kg-2.
m
cm (ms-1)
0
∞
1
40,02
2
20,2
3
13,5
4
10,1

21. Soluções de Ondas Lineares das Equações da Água Rasa
Vamos considerar caso do plano β-equatorial:
f = βy (2.1)
Onde β = 2Ω/a ⇒ Parâmetro de Rossby
∂u ∂ φ
−β v +
y =0 (2.2a)
∂t ∂x
∂v ∂φ
+β +
yu =0 (2.2b)
∂t ∂y
∂φ 2∂ u ∂v 
+c 
 ∂x + ∂y  = 0
 (2.2c)
∂t  

22. É conveniente transformar as equações para a forma adimensional,
utilizando as escalas:
1 1
[L ] = c
[T ] = 1 
2 2

 
   (2.3)
β  cβ
 
Fig. 2.1: Número de unidades de tempo adimensionais por dia (escala da
esquerda) ou escala de tempo [T] em dias (escala da direita) como
função de c = (gH)1/2. (Fonte: Silva Dias e Schubert, 1979)

23. Fig. 2.2: Número de unidades de comprimento adimensionais por
1000Km (escala da esquerda) ou escala de comprimento [L] em
quilômetros (escala da direita) como função de c = (gH)1/2. (Fonte: Silva
Dias e Schubert, 1979)

24. Usando c como escala para u e v e c2 = gH como escala de φ, tem-se:
∂
u
−v +
y
∂
=0
φ (2.4a)
∂
t ∂x
∂
v
+yu +
∂φ=0 (2.4b)
∂t ∂y
φ ∂ +v =
∂
+
u ∂
0 (2.4c)
∂t ∂x ∂
y
u  u 
Condições de fronteira:    
 v ( x , y , t ) =  v ( x + L x , y , t ) (2.5a)
φ  φ 
   
 
u
 
lim v  x, y , t ) =0 (2.5b)
(
y →∞
 
φ
 

25. Buscando soluções na forma de ondas planas (Ansatz de ondas planas):
   k 
u u
    ikx + k t
iω
 =v
v  k 
e (2.6)
φ k 
  
  φ
iω u k −yv k + φ =0
k ik k (2.7a)
dφ
iω k +
k v yu k + k
=0 (2.7b)
dy
dv k
iω φ +iku k +
k k =0 (2.7c)
dy

26. Na forma vetorial:
(iωkI + Ωk)ξk = 0 (2.8)
k ⇒ número de onda zonal
ξk = [uk, vk, φk]T ⇒ autovetor
ωk ⇒ freqüência temporal (autovalor)
 
0 −y ik 
 
d 
Ω =y 0 (2.9)
k
 dy 
 d  Operador linear (anti-
ik 0  hermitiano)

 dy 


27. É possível reduzir o sistema (2.7) a uma única equação diferencial
ordinária em vk, dada por
d 2vk
ˆ  2 k 2 
+ω - k +
 k
2
- y v k = 0
ˆ
dy 2
 ωk 
vk → 0 quando |y| → ∞
Solução:
y2
−
v k ( y) = e 2
H n ( y)
Desde que seja satisfeita a relação de dispersão abaixo:
k
ω -k2
2
+ = n+
2 1 , n = 0, 1, 2, .... (2.10)
k
ωk

28. Fig. 2.3: Diagrama de dispersão de algumas ondas lineares permitidas
pelo modelo (2.5). (Fonte: Silva Dias e Schubert, 1979).

29. Fig. 2.4: Diagrama da velocidade de grupo das ondas lineares permitidas
pelo modelo (2.5). (Fonte: Silva Dias e Schubert, 1979).

30. As autofunções são dadas por:
 i 
 − 2 (ω k,n,r − k)H n +1 (y) − in(ω k,n,r + k)H n −1 (y) y 2

ξ k,n,r (y) =  ( 2
)
ω k,n,r − k H n (y)
2  −2
e
(2.11)
 i 
 − 2 (ω k,n,r − k)H n +1 (y) + in(ω k,n,r + k)H n −1 (y)
  Para n > 0
H 0 (y) y 2
 0 e − 2
ξ k, − (y) =  (2.12)
1,3 
H 0 (y)
  Para n = -1 (Kelvin)
Estas autofunções formam um conjunto ortogonal e completo no espaço
das funções de quadrado integrável em (-∞, +∞ ).

31. Fig. 2.5: Estrutura espacial dos campos do vento e do geopotencial
associada às ondas de Rossby para n = 1. (Adaptado de Raupp, 2002.)

32. Fig. 2.6: Estrutura espacial dos campos do vento e do geopotencial
associada às ondas de gravidade-inerciais para n = 1. (Adaptado de
Raupp, 2002.)

33. Fig. 2.7: Estrutura espacial dos campos do vento e do geopotencial
associada às ondas mistas de Rossby-gravidade (n = 0). (Adaptado de
Raupp, 2002.)

34. Fig. 2.8: Estrutura espacial dos campos do vento e do geopotencial
associada à onda de Kelvin (n = -1). (Adaptado de Raupp, 2002.)

35. Solução Geral das Equações da Água Rasa Através do Método
Espectral
Modelo de equações primitivas forçado por um perfil de aquecimento
diabático dado por J(x,y,p,t).
∂u ∂ φ
−β v +
y κ
=− u (3.1a)
∂t ∂x
∂v ∂φ
+β u +
y κ
=− v (3.1b)
∂t ∂y
∂ ∂  1 ∂φ   ∂u ∂v  1 ∂  J  ∂  ∂φ 
 − +  = −
 σ ∂p   ∂x ∂y    +κ
 σp    (3.1c)
∂t ∂p     c p ∂p   ∂p  ∂p 
 
κ ⇒ coeficiente de dissipação de momento e de resfriamento
Newtoniano.

36. Dado que a equação da estrutura vertical (1.16), com C.F. (1.17a,b)
constitui um problema de Sturm-Liouville:
J J
u ( x, y, p, t ) = ∑ u j ( x, y, t )G j ( p) v( x, y , p, t ) = ∑v j ( x, y, t )G j ( p )
j =1 j =1
(3.2)
∂  J  J
 pσ  = ∑q j ( x, y, t )G j ( p )
J
φ( x, y, p, t ) = ∑φ j ( x, y, t )G j ( p )  
j =1
∂p   j =1
Onde os coeficientes de expansão são dados por:
p0 p0
u j ( x, y, t ) = ∫ u ( x, y, p, t )G ( p )dp v j ( x, y , t ) = ∫ v( x, y, p, t )G ( p)dp
0 0
(3.3)
p0 p0
∂ J 
φ j ( x, y, t ) = ∫ φ ( x, y, p, t )G ( p )dp q j ( x, y , t ) = ∫ 
 pσ  ( p ) dp
G
0 0
∂ 
p 

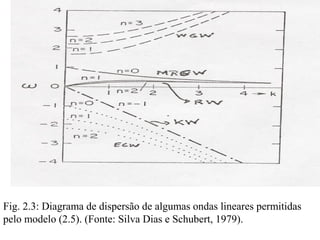
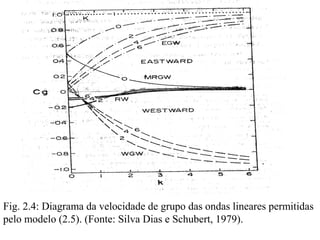
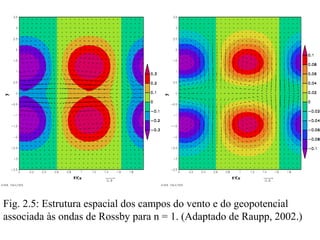
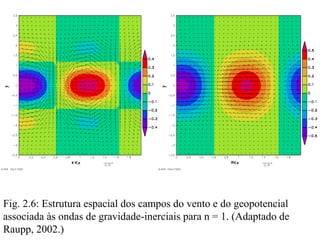
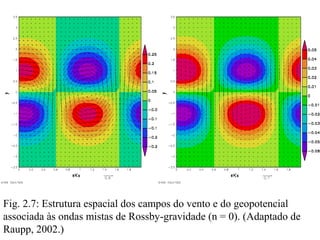
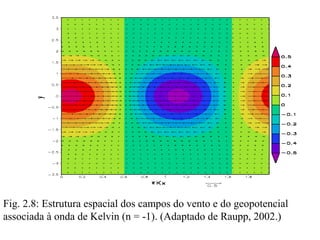
37. Substituindo (3.2) em (3.1), multiplicando as equações resultantes por
Gm(p), usando a equação da estrutura vertical (1.16) para cada um dos
modos verticais, integrando as equações resultantes no intervalo [0,p0] e
usando a ortogonalidade das autofunções Gj(p) obtém-se:
∂u j ∂φ j
− βyv j + = −κu j (3.4a)
∂t ∂x
∂ j
v φ
∂ j
+β j +
yu κ
=− v j (3.4b)
∂t ∂y
∂φ j  ∂u j ∂v j 
+c  2
 ∂x
j +  = c 2 ( q j − κφ j )
 j (3.4c)
∂t  ∂y 

38. Escrevendo na forma adimensional, usando as mesmas escalas usadas
anteriormente:
∂ξ
+Ω = F −κ
ξ ξ (3.5)
∂t
Onde ξ = [u(x,y,t), v(x,y,t), φ(x,y,t)]T
 ∂
0 −y 
 ∂x 
∂
Ω=  y 0 (3.6)
 ∂y 
∂ ∂ 
 0 
∂x
 ∂y 

F = [0, 0, Fφ]T com Fφ = q (c5β)-1/2 (3.7)

39. Dado que as autofunções ξk,n,r(y) formam um conjunto ortogonal e
completo em (-∞<y<∞)e que as funções trigonométricas complexas eikx
formam um conjunto ortogonal e completo no intervalo [-Lx,Lx]:
+∞ ∞ 3
G ( x, y , t ) = ∑∑∑g k , n , r (t )ξk , n , r ( y )e ikx
k =− n =− r =
∞ 1 1
/ (3.8)
gk,n,r(t) = < Gk(y,t) • ξk,n,r(y)> (3.9) , onde
+∞
G k ( y, t ) • ξ k ,n ,r ( y ) = ∫ (g
−∞
1k )
( y, t )u k*,n,r ( y ) + g 2 k ( y, t ) v k ,n,r ( y ) + g1k ( y, t )u k*,n,r ( y ) + g 3k ( y, t )φ k*,n,r ( y ) dy
(3.10)
Lx
1
Gk ( y, t ) =
Lx ∫ G ( x, y, t )e −ikx dx
−L x
(3.11)

40. Dessa forma, as variáveis de estado e a forçante podem ser expressas por
suas respectivas expansões em série:
+∞ ∞ 3
ξ(x,y,t) = ∑ ∑ ∑ ck,n,r(t) ξk,n,r(y)eikx
k =−∞n=−1r =1
(3.12)
+∞ ∞ 3
F(x,y,t) = ∑ ∑ ∑ fk,n,r(t) ξk,n,r(y)eikx
k =−∞ n=−1r =1
Substituindo a equação (3.12) em (3.5), multiplicando escalarmente por
ξ*s,m,l(y)e-isx , integrando a expressão obtida no domínio todo e usando a
relação (2.8) e a ortogonalidade das autofunções ξk,n,r(y)eikx no domínio
[-Lx,Lx] X (-∞<y<∞):
dck ,n ,r (t )
− iωk ,n ,r ck ,n ,r (t ) = f k ,n ,r (t ) − κck ,n ,r (t ) (3.13)
dt
para cada k, n, r.

41. A solução geral é dada por:
t
+ ∫ f k ,n ,r ( s)e
( i ω k , n , r −κ ) t − ( iω k , n , r −κ )( s − t )
c k ,n ,r (t ) = c k ,n ,r (0)e ds (3.14)
0
Previsão de tempo Previsão climática
No caso de uma forçante estacionária, a solução é dada por:
ck ,n ,r (t ) = ck ,n ,r (0)e
( iωk ,n ,r −κ ) t
+
f k ,n,r
[iω k ,n ,r −κ]
[e ( iω k ,n , r − κ ) t
−1] (3.15)

42. Para κ = 0, ocorre ressonância com os modos geostróficos zonalmente
simétricos (k = 0 e ω = 0):
−iω k,n,1t
f k,n,1 (1 − e )
c0,n ,1 (t ) = lim = tf 0,n ,1 (3.16a)
ωk ,n ,1 →0 iω k,n,1
− iω k,-1,3 t
f k,-1,3 (1 − e )
c0, −1,3 (t ) = lim = tf 0, −1,3 (3.16b)
ω k , −1, 3 →0 iωk,-1,3
Um dos mecanismos que mantém a circulação média
zonal da atmosfera

43. No caso de uma forçante explosiva, i.e., cresce inicialmente, atinge um
máximo e passa a decrescer com o tempo
ˆ α 3 t 2 e −αt
f k , n , r (t ) = f k , n , r (3.17)
A solução é dada, na ausência de dissipação (κ=0), por:
α3 ˆ e iω k , n , r 1 − 1 + (α + iω ) t + 1 (α + iω ) 2 t 2  e − ( α + iω k , n , r ) t 
c k ,n ,r (t ) = f k ,n,r   
( α + iω k , n , r )  
k ,n,r
2
k ,n ,r 
 
(3.18)

51. Referências
MAJDA, A. J. Introduction to PDEs and Waves for the Atmosphere and Ocean.
Volume 9. American Mathematical Society, 2003. ISBN: 0-8218-2954-8.
HOLTON, J. An introduction to dynamic meteorology. 4th Edition. Elsevier Academic
Press, 2004.
A. E. GILL. Atmosphere-Ocean Dynamics. Volume 30. International Geophysics Series.
Editora: Academic Press (1982). ISBN: 0-12-283520-4
J. PEDLOSKY. Geophysical Fluid Dynamics – Second Edition. Editora: Springer. ISBN:
0-387-96387-1. ISBN: 3-540-96387-1.
 LEMES, M. A. M.; A. D. MOURA. Fundamentos de dinâmica aplicados à
Meteorologia e Oceanografia. 2ª Edição. Holos Editora Ltda-ME, 2002. ISBN: 85-86699-
33-0.
HALTINER, G. J.; R. T. WILLIAMS. Numerical prediction and dynamic meteorology.
Second Edition, 1980. Editora: Wiley. ISBN: 0471059714, 477 pp.

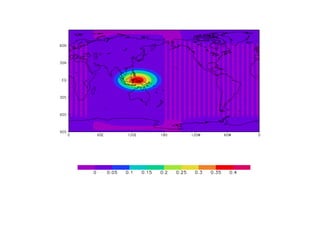
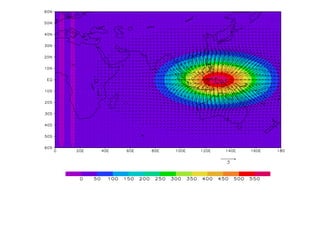
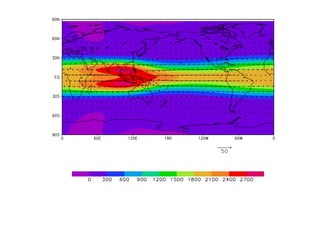
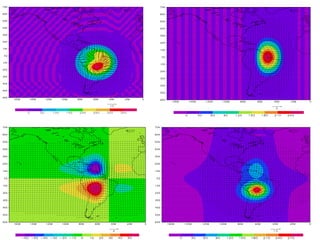
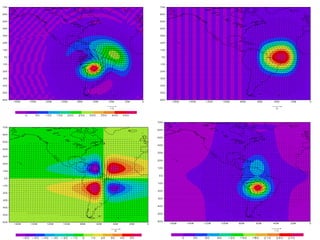
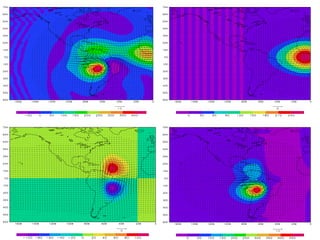
52. SILVA DIAS, P.L.; W. H. SCHUBERT. The dynamics of equatorial mass-flow
adjustment. Atmospheric Science Paper No. 312 (Department of Atmospheric Science
Colorado State University), Fort Collins, Colorado, USA, 1979.
 RAUPP, C. F. M. (2002). Efeitos de processos não lineares na influência inter-
hemisférica de fontes de calor. São Paulo, 2002. p. [Dissertação de Mestrado. Instituto de
Astronomia, Geofísica e Ciências Atmosféricas/Universidade de São Paulo].
 MATSUNO, T. Quasi-geostrophic motions in the equatorial area. J. Meteor. Soc.
Japan, 44, 25-43, 1966.
 John M. Wallace & Peter V. Hobbs. Atmospheric Science. First Edition: An
Introductory Survey, Editora: Academic Press, 1a edição (1977)