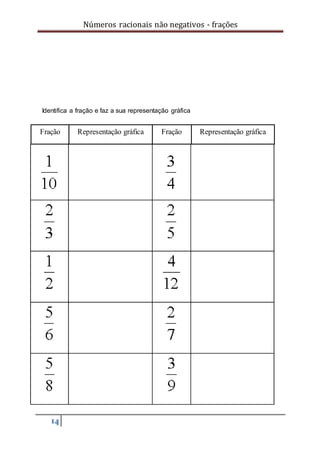
Este documento apresenta 5 tarefas relacionadas a frações para alunos do 2o ao 4o ano. Cada tarefa inclui objetivos, descritores e exercícios práticos para ensinar conceitos como dividir um todo, medir com frações e encontrar frações equivalentes. As atividades usam exemplos do mundo real e representações gráficas para tornar o assunto mais acessível.

1. Números racionais não negativos - frações
1
Ação de Formação
“O Novo Programa de Matemática e as
Metas… Que Metas”
Formanda: Eva cristina Barros Pereira
Formadora: Belmira Mariz
Penafiel, 17 de outubro de 2015

2. Números racionais não negativos - frações
2
Índice
Introdução....................................................................................................................................3
Trabalho de grupo.........................................................................................................................4
Domínio, Subdomínio, Objetivo e Descritores da tarefa 1.............................................................5
Tarefa 1 .................................................................................................................................6
Domínio, Subdomínio, Objetivo e Descritores da tarefa 2.............................................................9
Tarefa 2 ............................................................................................................................... 10
Domínio, Subdomínio, Objetivo e Descritores da tarefa 3........................................................... 15
Tarefa 3 ............................................................................................................................... 16
Domínio, Subdomínio, Objetivo e Descritores da tarefa 4........................................................... 19
Tarefa 4 ............................................................................................................................... 20
Domínio, Subdomínio, Objetivo e Descritores da tarefa 5........................................................... 22
Tarefa 5................................................................................................................................ 23
Conclusão/reflexão..................................................................................................................... 27

3. Números racionais não negativos - frações
3
Introdução
O gosto pela matemática foi uma das razões que me levaram a participar
nesta formação.
Hoje em dia a matemática, apresenta-se como um desafio cadavez mais
exigente, que nos leva a uma procura constante de novas formas de ensinar.
É certo que a matemática, tal como se apresenta, proporcionao
desenvolvimento de certas capacidades, que até então estavam um pouco
esquecidas.
Desta forma, estando a matemática presente por todo o lado, não podemos
permanecer estanques e alheios. É importante aprendermos, formas lúdicas e
divertidas de levar a matemática às nossas crianças.
“ Umbom ensino da matemática forma melhores hábitos de pensamento e habilita o
individuo a usar melhor a sua inteligência “.
“Irene de Albuquerque”

4. Números racionais não negativos - frações
4
Trabalho de Grupo
Números Racionais Não negativos
Frações

5. Números racionais não negativos - frações
5
Tarefa 1: 2º ano
Domínio: Números e Operações (NO2)
Subdomínio: Números racionais não negativos
Objetivo Geral: Dividir a unidade
Descritores: Utilizar a fração 1/2 para referir cada uma das partes de um todo dividido em
duas partes equivalentes.

6. Números racionais não negativos - frações
6
Tarefa 1
A Francisca tem uma grande amiga, a Elsa. Elas fazem tudo juntas, desde
pequenas. A Francisca sempre dividiu o seu lanche com Elsa e vice-versa, assim
elas têm um lanche diversificado.
Na aula de matemática, elas aprenderam que podem representar a divisão que
fazem com uma fração: 1/2, que é, na verdade, a parte que cada uma come.
Como a Francisca e a Elsa fariam a divisão dos seus lanches, abaixo? Para o
representares, divide o desenho igualmente em duas partes e pinta apenas uma
delas. Depois, anota nos quadrinhos a fração que representa a parte pintada:
Além de aprender o número fracionário, descobriram ainda algo muito
importante. Observa:
denominador
1
2
Esta parte da fração representa o lanche
inteiro delas, antes de ser repartido em duas
partes iguais.
Esta parte da fração representa em quantas
partes iguais o lanche é dividido.
numerador

7. Números racionais não negativos - frações
7
Francisca entendeu muito bem esta parte, mas teve uma outra dúvida: houve
alguns dias, em que ela e sua amiga Elsa não dividiam 1 inteiro pela metade. Se ela
levasse 10 rebuçados para a escola, por exemplo, 5 seriam da sua amiga.
A professora explicou então, que nesse caso, ela tem 1 grupo de 10
rebuçados, então se o grupo for dividido em duas partes iguais, cada uma irá
ganhar 5 rebuçados.
O registro desta operação em fração ficaria da seguinte forma.
Na verdade, basta dividir o número total de componentes do grupo por 2.
Vê se consegues também...
Conta o total de elementos de cada grupo, divide-o por 2 e pinta metade
desse total. Depois, regista a operação como fez a professora da Francisca e da
Elsa:
de 10 rebuçados = 5 rebuçados
1
2

8. Números racionais não negativos - frações
8
 Qual é o total de gelados? __________
 Quanto é a metade de gelados? ___________
 Como se regista em forma de fração? ___________________________
 Qual é o total de balões? __________
 Quanto é a metade dos balões? ___________
 Como se regista em forma de fração? ____________________________
 Qual é o total de afias? __________
 Quanto é a metade das afias? ___________
 Como se regista em forma de fração? ____________________________

9. Números racionais não negativos - frações
9
 Qual é o total de sapos? __________
 Quanto é a metade dos sapos? ___________
 Como se regista em forma de fração? ____________________________
Tarefa 2 (3º ano)
Domínio: Números e Operações (NO3)
Subdomínio: Números racionais não negativos
Objetivo Geral: Medir com frações
Descritores:
- Utilizar corretamente os termos «numerador» e «denominador»;
- Utilizar corretamente os numerais fracionários;
- Utilizar as frações para designar grandezas formadas por certo número de partes
equivalentes a uma que resulte de divisão equitativa de um todo.

10. Números racionais não negativos - frações
10
Tarefa 2
No caso de Francisca e da Elsa, percebemos que, ao dividir o lanche, cada
uma fica com do lanche. O 1 (numerador) representa a
parte do lanche com a qual cada uma fica. O 2 (denominador) mostra o total de
partes ou pedaços em que foi dividida a peça ou grupo.
Quando pintou a metade dos lanches ou dos grupos, representou a fração
correspondente.
Imagine que tem um chocolate com três quadradinhos para formar uma barra.
Comeu apenas um quadradinho do total de três. Para representar o total comido em
forma de fração utilizo.
O 1 (numerador) representa a parte comida e o 3 (denominador) mostra a
quantidade de partes que estavam disponíveis. Se comeres dois pedaços, então a
fração será.
Pinta a parte da figura representada pela fração:
1
2
1
3
2
3
1
4
3
4
4
4

11. Números racionais não negativos - frações
11
Identifica a fração representada pela parte pintada de cada figura e regista
Fração Representação gráfica Fração Representação gráfica

12. Números racionais não negativos - frações
12
Identifica a fração e pinta a parte do desenho que a representa:
Fração Representação gráfica Fração Representação gráfica

13. Números racionais não negativos - frações
13
NOME: ____________________________________________________
DATA:
Fração Representação gráfica Fração Representação gráfica

14. Números racionais não negativos - frações
14
Identifica a fração e faz a sua representação gráfica
Fração Representação gráfica Fração Representação gráfica

15. Números racionais não negativos - frações
15
Tarefa 3 (3º ano)
Domínio: Números e Operações (NO3)
Subdomínio: Números racionais não negativos
Objetivo Geral: Medir com frações
Descritores:
- Identificar <reta numérica> como a reta suporte de uma semirreta utilizada para representar
números não negativos, fixada uma unidade de comprimento;
- Fixar um segmento de reta como unidade e identificar uma fração;
- Fixar um segmento de reta como unidade de comprimento e representar números naturais e
frações por pontos de uma semirreta dada, representando o zero pela origem e de tal modo
que o ponto que representa determinado número se encontra a uma distância da origem igual a
esse número de unidades.

16. Números racionais não negativos - frações
16
Tarefa 3
Podemos representar frações equivalentes, isto é, frações que representam o
mesmo valor ou a mesma quantidade numa reta numérica. Para tal, devemos dividir
a linha reta no número mostrado pelo denominador.
Observa na tabela abaixo os denominadores das frações, a representação
gráfica por divisão de inteiro, a representação de grupo e, finalmente, a
representação na reta numérica:
Para fazer a marcação da fração, basta observar o numerador e fazer um
círculo na porção da reta ao qual ele se refere. Vê o exemplo:
Fração Divisão de inteiro Representação de grupo Representação em linha
O denominador é 5, então a reta foi
dividida em 5 partes. O numerador é 2,
portanto o círculo está marcado no
segundo tracinho, já que o primeiro
sempre representa o 0.

17. Números racionais não negativos - frações
17
Vamos ver agora se compreendeste como se representa a fração em forma de
linha. Observa a linha e anota qual é a fração lhe corresponde:
2
5

18. Números racionais não negativos - frações
18
Nesta atividade, terás a fração e a reta. Basta representar a fração colocando o
círculo no local correto:

19. Números racionais não negativos - frações
19
Tarefa 4 (3º ano)
Domínio: Números e Operações (NO3)
Subdomínio: Números racionais não negativos
Objetivo Geral: Medir com frações
Descritores:
- Utilizar corretamente os numerais fracionários;
- Utilizar as frações para designar grandezas formadas por certo número de partes
equivalentes a uma que resulte da divisão equitativa de um todo.

20. Números racionais não negativos - frações
20
Tarefa 4
1. Lê as instruções para colorir cada figura:
a. Pinta 2 pedaços de azul e 4 pedaços de amarelo.
b. Pinta 1 pedaço de verde, 6 pedaços de laranja e deixa o restante branco.
c. Pinta a próxima figura da forma que desejares e depois escreve as frações
que representam as partes pintadas:
Qual fração representa a parte amarela?
Qual fração representa a parte azul?
Qual fração representa a parte branca?
Qual fração representa a parte laranja?
Qual fração representa a parte verde?
________________________________
________________________________
________________________________
________________________________
________________________________
________________________________
_______________________________

21. Números racionais não negativos - frações
21
2. A Dona Maria faz uns deliciosos bolinhos para vender. Ela recebeu duas
encomendas esta semana. A massa dos bolinhos é sempre a mesma, o que muda é
a cobertura.
Lê os pedidos e pinta as coberturas de acordo com o que está escrito:
de cada sabor abaixo:
 Chocolate
 Morango
 Limão
 Maracujá
1
4
de chocolate
de limão
de morango
4
16
7
16
5
16

22. Números racionais não negativos - frações
22
Tarefa 5 (4º ano)
Domínio: Números e Operações (NO4)
Subdomínio: Números racionais não negativos
Objetivo Geral: Medir com frações
Descritores:
- Identificar frações equivalentes utilizando medições de diferentes grandezas (3ºano);
- Reconhecer que multiplicando o numerador e o denominador de uma determinada fração
pelo mesmo número natural se obtém uma fração equivalente;
- Simplificar frações nos casos em que o numerador e o denominador pertençam
simultaneamente à tabuada do dois ou do cinco ou sejam ambos múltiplos de 10.

23. Números racionais não negativos - frações
23
Tarefa 5
A Francisca levou para a escola um pedaço de bolo de chocolate que a sua mãe
fez. Ela dividiu metade do pedaço do bolo para dar à sua grande amiga Elsa.
Qual é a fração que representa a quantidade de bolo com que, cada uma delas,
ficou?
A Francisca dividiu a sua parte pela metade e comeu uma parte, ou seja,
A Elsa, por sua vez, cortou sua parte de bolo em 4 pedaços iguais e comeu 2
desses pedaços, ou seja,
Representa abaixo, em forma de desenho, a divisão feita pela Francisca e pela
Elsa e, em seguida, pinta a quantidade de bolo que elas já comeram:
Quem comeu a maior quantidade de bolo? Por quê?
___________________________________________________________________
___________________________________________________________________
2
4
1
2
Francisca Elsa

24. Números racionais não negativos - frações
24
1
2
2
4
6
12
X2 X3
X2 X3
==
Quando diferentes frações representam a mesma parte de um inteiro, são
chamadas de frações equivalentes.
Pinta a quantidade de pedaços representada pelo numerador e observa como
mostram a mesma quantidade de uma unidade
Sendo assim, as duas frações mostradas são equivalentes, pois uma é
correspondente à mesma quantidade da outra, portanto =
Um modo prático de encontrar frações equivalentes é multiplicar ou dividir o
numerador e o denominador da fração por um mesmo número, que seja diferente de
zero. Observa:
 Agora encontra duas frações equivalentes
multiplicando o numerador e o denominador por 2:
= =1
5
=
1
2
2
4
1
2
2
4
12
6
4
2
2
1
:3 :2
:3 :2
=

25. Números racionais não negativos - frações
25
= =
 Encontra duas frações equivalentes, multiplicando numerador e
denominador por 3:
= =
= =
 Encontra duas frações equivalentes, dividindo numerador e denominador
por 2:
 = =

 = =
3
4
12
24
1
4
1
5
16
36

26. Números racionais não negativos - frações
26
 Encontra duas frações equivalentes, dividindo numerador e denominador
por 5:
25
5
35
25
 Divide as formas de modos diferentes e pinta representações de fração, em
cada uma delas, de maneira que as frações fiquem equivalentes.

27. Números racionais não negativos - frações
27
Conclusão/reflexão
Com a apresentação/sugestão dos exercícios propostos acho que de uma forma sugestiva e
divertida, as crianças aprendem com relativa facilidade este tema.
Com a explicação e exemplos que lhes são dados é fácil resolver os exercícios.
Não me foi possível aplicar estes exercícios, pois estou colocada na Educação Especial.
Contudo numa próxima oportunidade irei, sem dúvida, aplicar e verificar até que ponto são
compreensíveis para os diversos anos de escolaridade.
Contudo, nada disto se consegue apenas com estes exercícios, tem que haver muitas
repetições, muita insistência e muito trabalho.
Alguns críticos às Metas Curriculares, dizem que estas são demasiado exigentes. Como pode
uma criança do primeiro ou de qualquer ano saber isto, aprender aquilo, em tão pouco tempo?
Impõe-se um grau de exigência que dificilmente a maioria dos alunos conseguirá atingir…
dizem até que as Metas “estão mal feitas” e quem as elaborou não conhece as crianças e
percebe pouco do assunto.
Citando algumas palavras de Mário Nogueira e que eu subscrevo na integra.
“…O que me parece, realmente, é que se pretende fazer uma seleção fina, exigente, logo
desde cedo. Querem saber quem é capaz e quem tem dificuldades para obter aquele resultado
que, propositadamente, é difícil de alcançar. Como se costuma dizer “só está ao alcance dos
melhores”. Essa é a seleção que pretendem fazer, para separar. Como se faz com qualquer
produto num contexto de mercado. Separa-se o melhor, do médio e do que é defeituoso. O
mercado paga bem pelo produto de elevada qualidade e desvaloriza o resto, não lhe interessa.
O produto de elevada qualidade é pago adequadamente, o que é médio constitui a linha branca
e é adquirido pela maioria, depois há o que sobra, de qualidade inferior, que é consumido por
quem apenas tem acesso aos mínimos e, por norma, é-lhe atribuído por via de apoio social.
Esta teoria de mercado é agora remetida para a Educação, para a mercantilização da Educação
em que o ensino também apresenta melhor ou pior qualidade, vende-se e compra-se conforme

28. Números racionais não negativos - frações
28
o poder de compra de quem o adquire. Falamos do que a Constituição da República define
como um bem social que deverá estar ao alcance de todos com elevada qualidade, mas que
agora deverá passar a obedecer a lógica diferente. Uma lógica neoliberal que é desumana e, a
partir de certo ponto, selvagem.”
Bibliografia
http://www.fenprof.pt/?aba=27&mid=115&cat=226&doc=8764
http://www.apm.pt/files/205600_METAS_CURRICULARES_MATEM_RT_5253df6f35875.
pdf
http://www.somatematica.com.br/frases3.php
http://www.dge.mec.pt/matematica