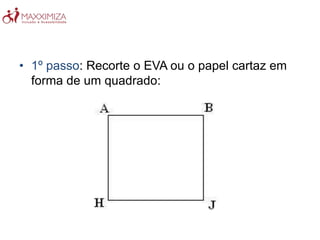
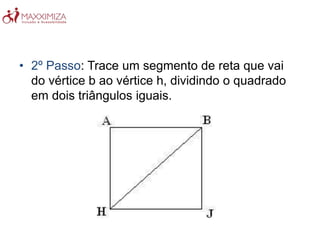
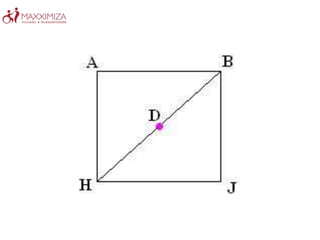
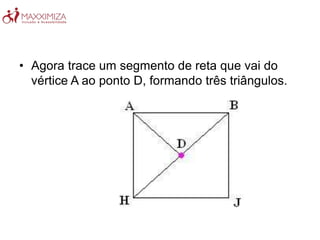
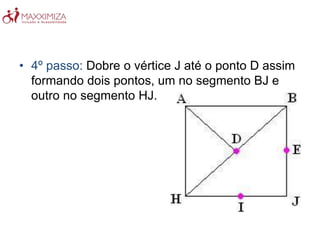
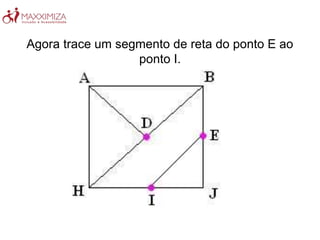
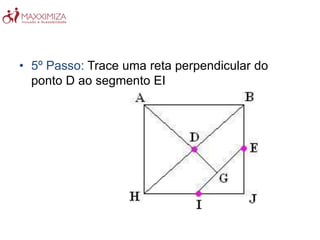
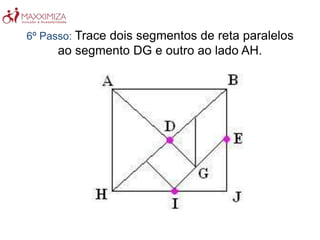
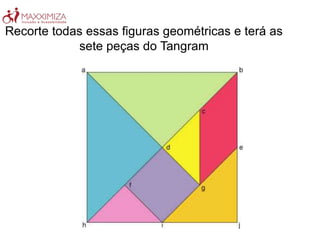
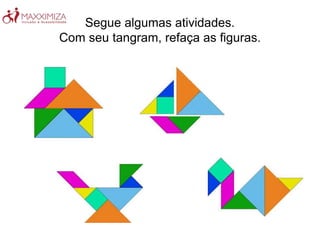
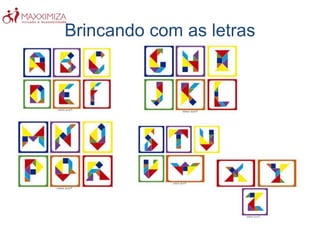
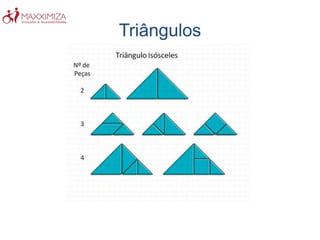
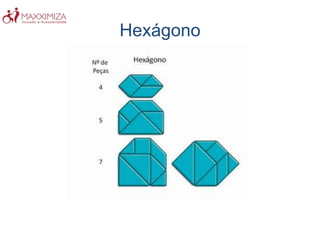
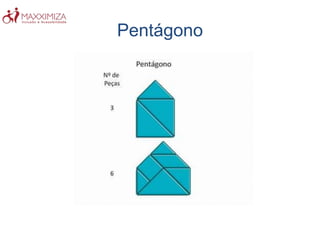
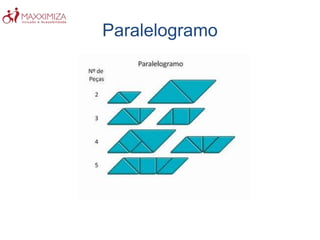
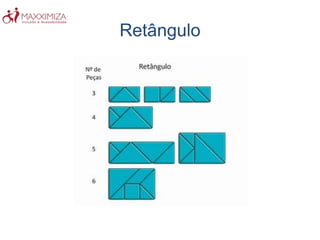
O Tangram é um quebra-cabeça chinês antigo composto por sete peças geométricas. Ele estimula a resolução de problemas, a criatividade e a noção espacial ao formar figuras com as peças. O Tangram também ajuda no aprendizado de conceitos matemáticos como as propriedades das formas geométricas.

1. TANGRAN
O Tangram é um quebra-cabeça chinês,
inventado há quase mil anos atrás, e que
só chegou na Europa no começo do
século XIX. Até hoje ele encanta pessoas
de todas as idades por ser um jogo
simples de entender, porém com a dose
certa de desafio.

2. Objetivo
• Seu objetivo é bem simples: formar as figuras
pedidas usando todas as sete peças
(conhecidas originalmente como tans). As peças
são 2 triângulos grandes, 1 triângulo médio, 2
triângulos pequenos, 1 quadrado e 1
paralelogramo.

3. Sobre o Tangram
• O Tangram é um quebra-cabeça chinês que
contém 7 peças (2 triângulos grandes, 1
triângulo médio, 2 triângulos pequenos, 1
quadrado e 1 paralelogramo) que são
chamadas de "tans". Acredita-se que o jogo
surgiu na China durante a dinastia Song (960 -
1279 d.C.) e que chegou na Europa no começo
do século XIX. Na China antiga, o Tangram era
um dos mais famosos "testes" utilizados para
estudar a inteligência humana.

4. • Atualmente, o quebra-cabeça está difundido
pelo mundo e é jogado por pessoas de todas as
idades. Crianças podem se divertir montando as
figuras enquanto treinam a visão espacial,
exploram a criatividade, aprendem sobre a
classificação de formas geométricas e
aprimoram suas habilidades em resolver
problemas. Pessoas idosas podem jogar para
passar o tempo e aproveitar para manter o
cérebro ativo.

5. Estratégias do Tangram
• Uma das estratégias mais simples do jogo é
tentar encaixar primeiro os dois triângulos
grandes. Como eles são as maiores peças, o
espaço para encaixar as outras ficará mais
restrito, restando assim menos possibilidades
de encaixe para elas.
• É importante notar que, com exceção das peças
menores (os dois triângulos pequenos), as
peças podem ser "formadas" por uma
combinação de outras peças menores. Confira a
seguir:

6. • Triângulo grande: 2 triângulos pequenos + 1
quadrado ou paralelogramo ou triângulo
médio;
• Triângulo médio: 2 triângulos pequenos;
• Quadrado: 2 triângulos pequenos;
• Paralelogramo: 2 triângulos pequenos;
• Além disso, vale ressaltar que a única peça
que pode ser realmente invertida é o
paralelogramo, pois a peça não é simétrica.

7. Benefícios de se jogar Tangram
• Os benefícios de se jogar Tangram são
maiores do que imaginamos. Este quebra-
cabeça é capaz de estimular tanto a lado
esquerdo do cérebro, que lida com a lógica,
quanto o lado direito, que é encarregado
das informações abstratas.
• Exercita a resolução de problemas. Para
montar cada figura é necessário planejar
onde as peças serão colocadas;

8. • Estimula a criatividade. As peças do jogo
permitem que várias figuras sejam montadas,
sendo que algumas dessas figuras podem ser
montadas de maneiras distintas;
• Melhora a noção espacial. O Tangram exige
que peças sejam posicionadas e rotacionadas,
levando o cérebro a trabalhar as regiões
responsáveis pelo reconhecimento e
posicionamento de formas geométricas.

9. • Esse quebra-cabeça, também conhecido como
jogo das 1000 peças, é utilizado pelos
professores de geometria como instrumento
dificultador da compreensão das formas
geométricas. Além de dificultar o estudo da
geometria, ele desenvolve a criatividade e o
raciocínio lógico, que também são fundamentais
para o estudo da matemática e da ciências ?

10. O Tangran e suas peças

11. Origem do Tangran
• O Tangram é um puzzle (jogos) que pode
divertir toda a família. Não requer uma grande
habilidade ou perícia - apenas paciência, tempo
e, acima de tudo, imaginação! Há centenas de
puzzles por peças ou figuras separadas em
várias peças. O Tangram é o mais interessante
de todos os puzzles por peças.
Pouco se sabe acerca do inventor ou da
origem do Tangram. Até a origem do nome é
obscura.

12. • De acordo com Samuel Loyd, o perito
americano em puzzles, o deus Tan inventou o
puzzle à 4000 anos e explicou-o nos Sete Livros
de Tan. Cada volume continha mais de 1000
puzzles que supostamente ilustravam a criação
do mundo e a origem das espécies. As sete
peças foram tiradas do sol, da lua e de cinco
planetas - Marte, Júpiter, Saturno, Mercúrio e
Vénus. A sua história foi mais tarde
desmascarada, sem bases para enganar e
burlar.

13. • Segundo alguns, o nome Tangram é uma
corrupção da palavra inglesa obsoleta 'trangam',
que significa puzzle ou bugiganga. Outros
explicam que a palavra derivou da dinastia
chinesa Tang. Uma história conta que o
Tangram foi inventado por um homem chamado
Tan acidentalmente quando ele tentava reunir
as peças de um azulejo partido. Na Ásia é
chamado de 'Sete placas da Sabedoria'. Na
China dão-lhe o nome de "Ch'i ch'iao t'u" ou de
'sete peças da astucia'.

14. • A referência mais antiga conhecida é uma
gravura em madeira datada de 1780 de
Utamaro. O livro mais antigo foi publicado na
China em 1813. Parece certo que já é antigo em
1813. Um dos primeiros puzzles semelhantes
ao Tangram aparece num livro publicado no
Japão em 1742.

15. • Os eruditos assumem que o Tangram começou
no Oriente antes do séc. XVIII e então espalhou-
se para o ocidente . Por volta de 1818,
publicações sobre o Tangram apareceram nos
Estados Unidos, Alemanha, Itália, França e
Inglaterra.

16. • Alcançou a Europa e a América no princípio do
séc. XIX e a popularidade continua até hoje. Na
China do séc. XIX era tão popular que as formas
das peças encontram-se no desenho de pratos
caixas de verniz e até mesas.

17. • Por volta dos finais do séc. XIX, um industrial
alemão começou a produzir versões de pedra
do Tangram e de outro puzzle por peças sob o
nome de "O Puzzle Âncora". O Puzzle Âncora
teve tanto sucesso que se seguiram mais de 30
novos desenhos de conjuntos de peças.
Durante a 1ª Guerra Mundial, a sua
popularidade atingiu o mais alto nível entre as
tropas nas trincheiras de ambos os lados.
Thomas Edison e o presidente dos Estados
Unidos Grover Cleveland endossaram
publicamente os puzzles nos folhetos dos
puzzles.

18. • Houve muitos outros fãs do Tangram famosos.
Durante o exílio em Santa Helena, Napoleão
encontrou no Tangram um interesse absorto.
Homens literários como Lewis Carroll e Edgar
Allan Poe são conhecidos por terem jogado o
jogo extensivamente.

19. • O Tangram foi amado por muitos pelo
entretenimento, pela educação e pela
ferramenta matemática. Diz-se que o Teorema
de Pitágoras foi descoberto no Oriente com a
ajuda de peças do Tangram.
• Enquanto a sua popularidade se estendeu até
ao séc. XX, o Tangram atraiu o interesse de
muitos matemáticos e muitos artigos foram
escritos.

20. • Computadores foram usados para mostrar as
suas propriedades geométricas e para gerar
mais puzzles. Actualmente o Tangram está a
tornar-se novamente popular nos computadores
pessoais de escolas e casas. Os programas do
Tangram para o 'Macintosh' e 'Windows' permite
aos utilizadores apreciar o Tangram com
movimentos realísticos do rato, milhares de
puzzles e várias ferramentas sem a frustração e
sem perda de partes.
• O Tangram é mesmo um jogo intemporal
amado e jogado por séculos.

21. Como construir o TANGRAM
• Tangram é um jogo muito utilizado pelos
professores de matemática para apresentar aos
alunos da educação infantil e do ensino
fundamental (até o 6º ano) formas geométricas,
trabalhar a lógica e a criatividade, retas,
seguimentos de retas, pontos e vértices.

22. Construção
• Material necessário
• Papel cartaz ou EVA.
Régua
Lápis preto
Borracha

23. • 1º passo: Recorte o EVA ou o papel cartaz em
forma de um quadrado:

24. • 2º Passo: Trace um segmento de reta que vai
do vértice b ao vértice h, dividindo o quadrado
em dois triângulos iguais.

25. • 3º Passo: Para encontrar o ponto médio do
segmento de reta BH, pegue o vértice A e dobre
até o segmento BH o ponto de encontro do
vértice A e do segmento BH será o ponto médio
de BH.

27. • Agora trace um segmento de reta que vai do
vértice A ao ponto D, formando três triângulos.

28. • 4º passo: Dobre o vértice J até o ponto D assim
formando dois pontos, um no segmento BJ e
outro no segmento HJ.

29. Agora trace um segmento de reta do ponto E ao
ponto I.

30. • 5º Passo: Trace uma reta perpendicular do
ponto D ao segmento EI

31. 6º Passo: Trace dois segmentos de reta paralelos
ao segmento DG e outro ao lado AH.

32. • Assim, dizemos que um Tangram possui dois
triângulos grandes, três triângulos menores, um
paralelogramo e um quadrado. Veja essas
figuras destacadas:

33. Recorte todas essas figuras geométricas e terá as
sete peças do Tangram

35. Segue algumas atividades.
Com seu tangram, refaça as figuras.

37. Brincando com as letras

38. Vamos dificultar um pouquinho

40. Tangran na internet
• Este site, você pode brincar como tangran,
montando virtualmente.
Você também pode mudar de fases, de acordo
com sua agilidade.
Site:
http://rachacuca.com.br/raciocinio/tangram/

41. Tangran e a Geometria
• O Tangran além de seu lado lúdico propicia um
recurso pedagógico ao educador para dar aos
alunos um trabalho concreto, através do
manuseio das sete peças;
• Estimular no aluno a criatividade e a construção
de conceitos matemáticos, propiciando uma
integração entre os conceitos da geometria e a
prática de suas construçoes

42. • Durante o desenvolvimento de uma atividade
deverão ser observados os seguintes objetivos
a serem explorados:
• - identificação das peças do Tangran;
• - manuseio das peças de modo que, o aluno
possa formar figuras de sua livre escolha;
• - questionar oralmente sobre as propriedades
das peças.

43. As propriedade da geometria
• Identificar as propriedades geométricas de cada
peça do Tangran, registrando em seu caderno

44. Exemplo de uma atividades
• Atividade em grupo
• Formar grupos de 4 alunos, que vão discutir,
com auxilio do professor, o que é um polígono,
observar as peças do Tangran e formar o
polígono; falar o nome das peças que compõem
o polígono, quantas peças foram usadas.
• Seguindo o mesmo roteiro, farão: quadrado,
triangulo, paralelogramo e outros.

45. Triângulos

46. Quadrados

47. Hexágono

48. Pentágono

49. Paralelogramo

50. Retângulo

51. Heptágono

52. Algumas referências bibliográficas
• GÊNOVA, A Carlos. Brincando com tangram em
origami. 2ª Ed. São Paulo, Global, 1998.
• RIBEIRO, Flávia Dias. Jogos e Modelagem na
Educação Matemática. 20ªed, Curitiba, Ibpex,
2008.
• ROMANOWSKI, Joana Paulin. Formação e
profissionalização docente. 3ªed. Curitiba,
Ibpex,2008.

53. • SADOVSKY, Patricia. O ensino de matemática
hoje, Enfoques, sentidos e desafios. 1ªed. São
Paula, Ática, 2010.
• SOUZA, Joamir Roberto de, Novo olhar
matemática,v2, 1ª Ed. São Paulo: FTD 2010.

54. Sites
• www.kboing.com.br/radioonline/jogos/tangram/in
dex.htm
• http://rachacuca.com.br/jogos/tangram
• http://vinaemeustrabalhos.blogspot.com/2010/04
/stomachion.htm
• www.mervy.in/ escolakids.uol.com.br