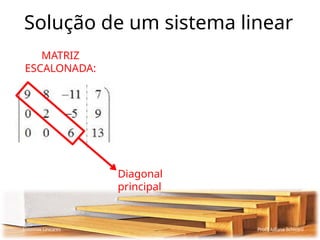
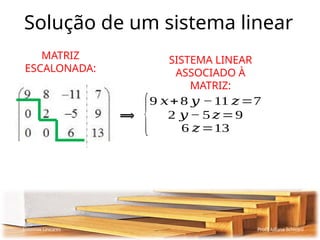
O documento aborda sistemas lineares, apresentando exemplos práticos para resolver equações que envolvem as compras de frutas feitas por diferentes indivíduos e sua relação com a determinação dos valores das frutas. Discute também a classificação dos sistemas lineares: possível e determinado (spd), possível e indeterminado (spi) e impossível (si), além de métodos de escalonamento para simplificação de sistemas. Por fim, descreve a representação matricial dos sistemas e os processos necessários para a resolução eficiente mediante escalonamento.













![Escalonamento
Sistemas Lineares Profª Juliana Schivani
{
𝑎+2 𝑏+3 𝑐=260
2 𝑎+𝑏 +𝑐=150
4 𝑎+3 𝑏+𝑐 =290
⟹
[
1 2 3 260
2 1 1 150
4 3 1 290 ]L2 L
⟵ 2 – 2L1
[
1 2 3 260
0 − 3 −5 −370
4 3 1 290 ]L3 L
⟵ 3 – 4L1
[
1 2 3 260
0 −3 − 5 −370
0 −5 −11 −750 ]
L3 3L
⟵ 3 - 5L2
[
1 2 3 260
0 −3 −5 − 370
0 0 − 8 − 400 ]{
𝑎+2 𝑏+ 3 𝑐=260
−3 𝑏 −5 𝑐=−370
−8 𝑐=−400](https://image.slidesharecdn.com/sistemas-240831220446-7d446447/85/SISTEMAS-LINEARES-MATEMATICA-2-ANO-ppsx-16-320.jpg)
![Escalonamento
Sistemas Lineares Profª Juliana Schivani
{
3 𝑥 − 𝑦+𝑧=2
𝑥 −2 𝑦 − 𝑧=0
2 𝑥 + 𝑦 +2 𝑧=2
⟹
[
3 −1 1 2
1 −2 − 1 0
2 1 2 2 ]L2 ⟷ L1
[
1 −2 − 1 0
3 −1 1 0
2 1 2 2 ]L2 ⟵ L2 – 3L1
[
1 −2 −1 0
0 5 4 2
2 1 2 2]L3 ⟵ L3 – 2L1
[
1 −2 −1 0
0 5 4 2
0 5 4 2]L3 ⟵ L3 – L2
[
1 −2 −1 0
0 5 4 2
0 0 0 0]
Duas equações < três variáveis ⟹
SISTEMA POSSÍVEL E INDETERMINADO (SPI)](https://image.slidesharecdn.com/sistemas-240831220446-7d446447/85/SISTEMAS-LINEARES-MATEMATICA-2-ANO-ppsx-17-320.jpg)
![Escalonamento
Sistemas Lineares Profª Juliana Schivani
{
2 𝑥− 𝑦+𝑧=−1
−5 𝑥− 20 𝑦 −15 𝑧=11
3 𝑥+3 𝑦+4 𝑧=3
⟹
[
2 −1 1 −1
−5 −20 −15 11
3 3 4 3 ]L2 ⟵ 2L2 + 5L1
[
2 − 1 1 −1
0 − 45 − 25 −17
3 3 4 3 ]L2 ⟵ 2L3 - 3L1
[
2 − 1 1 −1
0 − 45 − 25 −7
0 9 5 9 ]L3 ⟵ 5L3 + L2
[
2 − 1 1 −1
0 − 45 − 25 −7
0 0 0 38 ] SISTEMA IMPOSSÍVEL (SI)](https://image.slidesharecdn.com/sistemas-240831220446-7d446447/85/SISTEMAS-LINEARES-MATEMATICA-2-ANO-ppsx-18-320.jpg)

