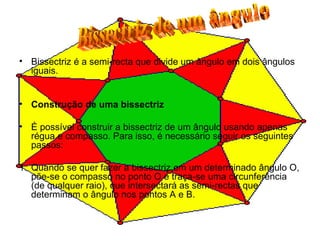
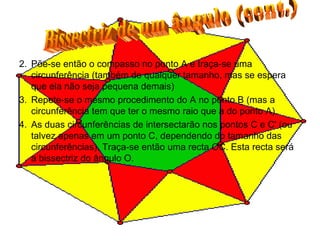
Este trabalho apresenta o conceito de simetria na biologia e em formas geométricas. Explica como construir a bissectriz de um ângulo usando régua e compasso. O objetivo é ensinar os colegas sobre simetria e como ela pode ser observada na natureza e na geometria.

1. Simetria Trabalho realizado por: Catarina Charrua nº4 Diogo Almeida nº 6 Margarida Melo nº 15 Mariana Costa nº 16

2. Ano lectivo 2007/2008 6º ano Turma g

3. Escola Básica 2.3 de Azeitão Novembro/Dezembro de 2007

4. Introdução diapos.5 Conceito de Simetria diapos.6 Simetria na Biologia diapos.7 Bissectriz de um ângulo diapos.8/9 Algumas fotografias sobre a simetria diapos.10 Conclusão diapos.11 Bibliografia diapos.12 Fim diapos.13 Índice

5. Neste trabalho iremos falar sobre a simetria, durante um mês pesquisamos sobre ela. Foi uma óptima pesquisa. Esperemos que gostem do nosso trabalho. Introdução

6. A simetria é uma característica que pode ser observada em algumas formas geométricas ou outros objectos. Se pusermos uma meia imagem, perpendicularmente à frente de um espelho vemos a imagem completa. Duas figuras são simétricas em relação a uma recta se, ao dobrarmos essa recta, elas coincidirem. A Simetria é a divisão imaginária de um ser vivo em partes semelhantes. Os animais e plantas podem ser assimétricos (não têm simetria), podem ter simetria radial ( onde existem diversos eixos de simetria) e podem ter simetria bilateral (quando há apenas um plano que divide o corpo em duas metades iguais). Conceito de Simetria

7. Na biologia, ao descrevermos o corpo de um animal ou uma parte de uma planta, fazemos diversas vezes referência ao eixo de simetria. Referimo-nos muito mais a simetria bilateral (apenas um eixo de simetria), pois o ser humano, tem simetria bilateral com algumas imperfeições; ou simetria radial (em que existem diversos eixos de simetria) como é o caso da estrela-do-mar. Estas características são muito importantes, pois ajudam-nos a classificar os animais, segundo a classificação de Lineu. Simetria na biologia

8. Bissectriz é a semi-recta que divide um ângulo em dois ângulos iguais. Construção de uma bissectriz É possível construir a bissectriz de um ângulo usando apenas régua e compasso. Para isso, é necessário seguir os seguintes passos: 1. Quando se quer fazer a bissectriz em um determinado ângulo O, põe-se o compasso no ponto O e traça-se uma circunferência (de qualquer raio), que intersectará as semi-rectas que determinam o ângulo nos pontos A e B. Bissectriz de um ângulo

9. 2. Põe-se então o compasso no ponto A e traça-se uma circunferência (também de qualquer tamanho, mas se espera que ela não seja pequena demais) 3. Repete-se o mesmo procedimento do A no ponto B (mas a circunferência tem que ter o mesmo raio que a do ponto A). 4. As duas circunferências de intersectarão nos pontos C e C' (ou talvez apenas em um ponto C, dependendo do tamanho das circunferências). Traça-se então uma recta OC. Esta recta será a bissectriz do ângulo O. Bissectriz de um ângulo (cont.)

10. Algumas fotografias sobre a simetria

11. Com este trabalho podemos aprender mais sobre a simetria. Achamos que com este trabalho podemos aprender e dar a conhecer á turma o que é a simetria. Esperamos que tenham gostado. Conclusão

12. www.wikipédia.pt CONCEIÇÃO, Maria Alexandra, Matematicamente Falando Motor de busca, imagens tiradas do Google. Bibliografia

13. Fim