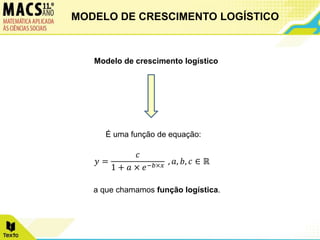
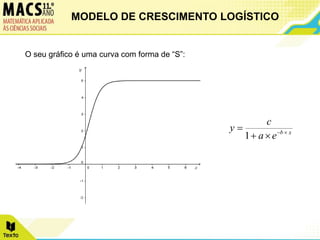
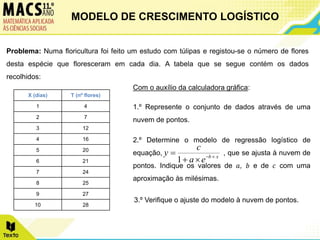
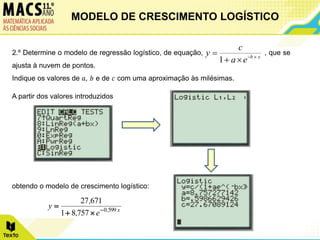
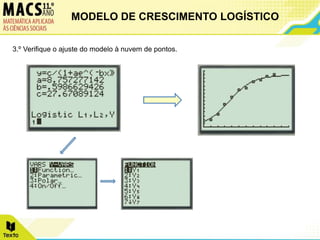
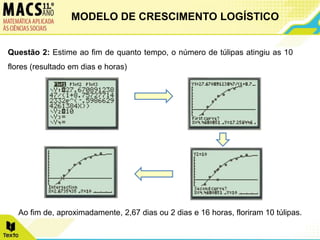
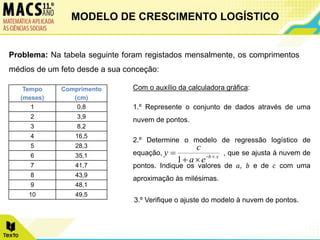
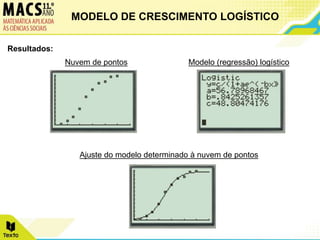
O documento descreve o modelo de crescimento logístico e apresenta dois exemplos de seu uso. Primeiro, analisa o crescimento de túlipas ao longo de 10 dias, ajustando os dados a uma função logística. Segundo, examina o crescimento fetal mensal de 0 a 10 meses, também ajustando os dados a uma função logística.

1. MODELO DE CRESCIMENTO LOGÍSTICO

2. Modelo de crescimento logístico
a que chamamos função logística.
MODELO DE CRESCIMENTO LOGÍSTICO
𝑦 =
𝑐
1 + 𝑎 × 𝑒−𝑏×𝑥
, 𝑎, 𝑏, 𝑐 ∈ ℝ
É uma função de equação:

3. O seu gráfico é uma curva com forma de “S”:
x
b
e
a
c
y 




1
MODELO DE CRESCIMENTO LOGÍSTICO

4. Problema: Numa floricultura foi feito um estudo com túlipas e registou-se o número de flores
desta espécie que floresceram em cada dia. A tabela que se segue contém os dados
recolhidos:
X (dias) T (nº flores)
1 4
2 7
3 12
4 16
5 20
6 21
7 24
8 25
9 27
10 28
Com o auxílio da calculadora gráfica:
1.º Represente o conjunto de dados através de uma
nuvem de pontos.
2.º Determine o modelo de regressão logístico de
equação, , que se ajusta à nuvem de
pontos. Indique os valores de 𝑎, 𝑏 e de 𝑐 com uma
aproximação às milésimas.
3.º Verifique o ajuste do modelo à nuvem de pontos.
x
b
e
a
c
y 




1
MODELO DE CRESCIMENTO LOGÍSTICO

5. 1.º Represente o conjunto de dados através de uma nuvem de pontos. X (dias) T (nº flores)
1 4
2 7
3 12
4 16
5 20
6 21
7 24
8 25
9 27
10 28
Introduzem-se os valores da tabela nas listas da calculadora:
e de seguida representa-se graficamente.
MODELO DE CRESCIMENTO LOGÍSTICO

6. 2.º Determine o modelo de regressão logístico, de equação, , que se
ajusta à nuvem de pontos.
Indique os valores de 𝑎, 𝑏 e de 𝑐 com uma aproximação às milésimas.
A partir dos valores introduzidos
obtendo o modelo de crescimento logístico:
x
b
e
a
c
y 




1
x
,
e
,
,
y 599
0
757
8
1
671
27




MODELO DE CRESCIMENTO LOGÍSTICO

7. 3.º Verifique o ajuste do modelo à nuvem de pontos.
MODELO DE CRESCIMENTO LOGÍSTICO

8. Questão 1: Estime o número de túlipas existentes ao fim de 15 dias.
No modelo determinado
basta substituir o valor da variável independente, 𝑥, por 15, pois nesta situação o
número de dias desempenha o papel da variável independente, sendo o número
de túlipas a variável dependente:
O número de túlipas será, aproximadamente, 28.
x
,
e
,
,
y 599
0
757
8
1
671
27




64067
,
27
757
,
8
1
671
,
27
757
,
8
1
671
,
27
15
599
,
0
15
599
,
0






 



 



y
e
y
e
y x
x
MODELO DE CRESCIMENTO LOGÍSTICO

9. Questão 2: Estime ao fim de quanto tempo, o número de túlipas atingiu as 10
flores (resultado em dias e horas)
Ao fim de, aproximadamente, 2,67 dias ou 2 dias e 16 horas, floriram 10 túlipas.
MODELO DE CRESCIMENTO LOGÍSTICO

10. Problema: Na tabela seguinte foram registados mensalmente, os comprimentos
médios de um feto desde a sua conceção:
Tempo
(meses)
Comprimento
(cm)
1 0,8
2 3,9
3 8,2
4 16,5
5 28,3
6 35,1
7 41,7
8 43,9
9 48,1
10 49,5
MODELO DE CRESCIMENTO LOGÍSTICO
Com o auxílio da calculadora gráfica:
1.º Represente o conjunto de dados através de uma
nuvem de pontos.
2.º Determine o modelo de regressão logístico de
equação, , que se ajusta à nuvem de
pontos. Indique os valores de 𝑎, 𝑏 e de 𝑐 com uma
aproximação às milésimas.
3.º Verifique o ajuste do modelo à nuvem de pontos.
x
b
e
a
c
y 




1

11. Resultados:
Nuvem de pontos
Ajuste do modelo determinado à nuvem de pontos
Modelo (regressão) logístico
MODELO DE CRESCIMENTO LOGÍSTICO