Este documento apresenta listas como estrutura de dados linear, discutindo sua definição formal, representação como tipo abstrato de dados e implementações possíveis na memória do computador como estruturas contíguas e encadeadas. Operações básicas como inserção, busca, acesso a elementos e remoção são demonstradas para listas implementadas como vetores contíguos.

1. Listas: Conceito e
estáticas
Prof: Sergio Souza Costa

2. Sobre mim
Sérgio Souza Costa
Professor - UFMA
Doutor em Computação Aplicada (INPE)
prof.sergio.costa@gmail.com
https://sites.google.com/site/profsergiocosta/home
http://www.slideshare.net/skosta/presentations?order=popular
https://twitter.com/profsergiocosta
http://gplus.to/sergiosouzacosta

3. Roteiro
●
●
●
Lista: Definição e tipo abstrato de dados.
Lista como estrutura de dados contígua.

4. Roteiro
●
●
●
●
Lista: Definição e tipo abstrato de dados.
Lista como estrutura de dados contígua.
Lista como estrutura encadeada.
Codificação de listas encadeadas em C.

5. Exemplos
de listas

6. Exemplos
de listas
Coisas a fazer
Compras
Catálogo telefônico

7. Qual propriedade é comum a
todas estas listas ?

8. Qual propriedade é comum a
todas estas listas ?
Linearidade

9. LISTA: DEFINIÇÃO FORMAL
Um lista L é uma coleção de n elementos x1, x2, x3
... Xn, para n >= 0.
1
Se n > 0, entao x1 é o primeiro e xn o último
elemento.
2
Para i = {1,2,...,n}, xi é precedido por xi-1 é
seguido por xi+1.
3
Se os elementos x1..xn são do mesmo tipo a lista é
denominada homogênea, caso contrário é
heterogênea.
4
Se n é igual a 0, então a lista é vazia.

10. LISTA: Tipo de dados abstrato
Descrevendo listas como um tipo abstrato de dados,
com 5 operações básicas.
Operação
Descrição
Tamanho (L)
Retorna o número de elementos de L
Inserir (L,x)
Insere um elemento x a L
Busca (L, x)
Busca um elemento x em L, retorna seu indice.
ElementoEm(L, i)
Retorna um elemento de L localizado em i.
Remove (L, i)
Remove um elemento de L localizado em i.

11. Qual a vantagem de descrever
as estruturas de dados como
tipos abstrato de dados ?

12. Qual a vantagem de descrever
as estruturas de dados como
tipos abstrato de dados ?
Abstrair os detalhes da
implementação,
ocultando a
representação
computacional. TAD
define a interface
apenas.

13. Qual a vantagem de descrever
as estruturas de dados como
tipos abstrato de dados ?
Pode então mudar a
es
Abstrair deentação
repres detalh
tação.
sobre a implemenal sem que
computacion
Ocultacliereprdaentação
o r a nte es aplicação
compuerceba”.. TAD
“p tacional
define a interface
apenas.

14. Como representar as listas na
memoria do computador?

15. Como representar as listas na
memoria do computador?
Estruturas contíguas
Estruturas Encadeadas

16. Como representar as listas na
memoria do computador?
Estruturas contíguas
Estruturas Encadeadas

17. Representação computacional na memoria
Áreas contíguas da
memoria, x2 é
adjacente a x1 e x3.
x1
x2
x3
x4
xxxx
xxxx
xxxx
xxxx
1
2
3
4
xn
...
xxx
n

18. Representação computacional na memoria
Áreas contíguas da
memoria, x2 é
adjacente a x1 e x3.
x1
x2
x3
x4
xxxx
xxxx
xxxx
xxxx
1
2
3
4
xn
...
xxx
n
Qual estrutura que vocês trabalham
que tem esta propriedade?

19. Representação computacional na memoria
Áreas contíguas da
memoria, x2 é
adjacente a x1 e x3.
x1
x2
x3
x4
xxxx
xxxx
xxxx
xxxx
1
2
3
4
xn
...
xxx
n
Qual estrutura que vocês trabalham
que tem esta propriedade?
Os arranjos, também conhecido como
vetores.

20. Definição
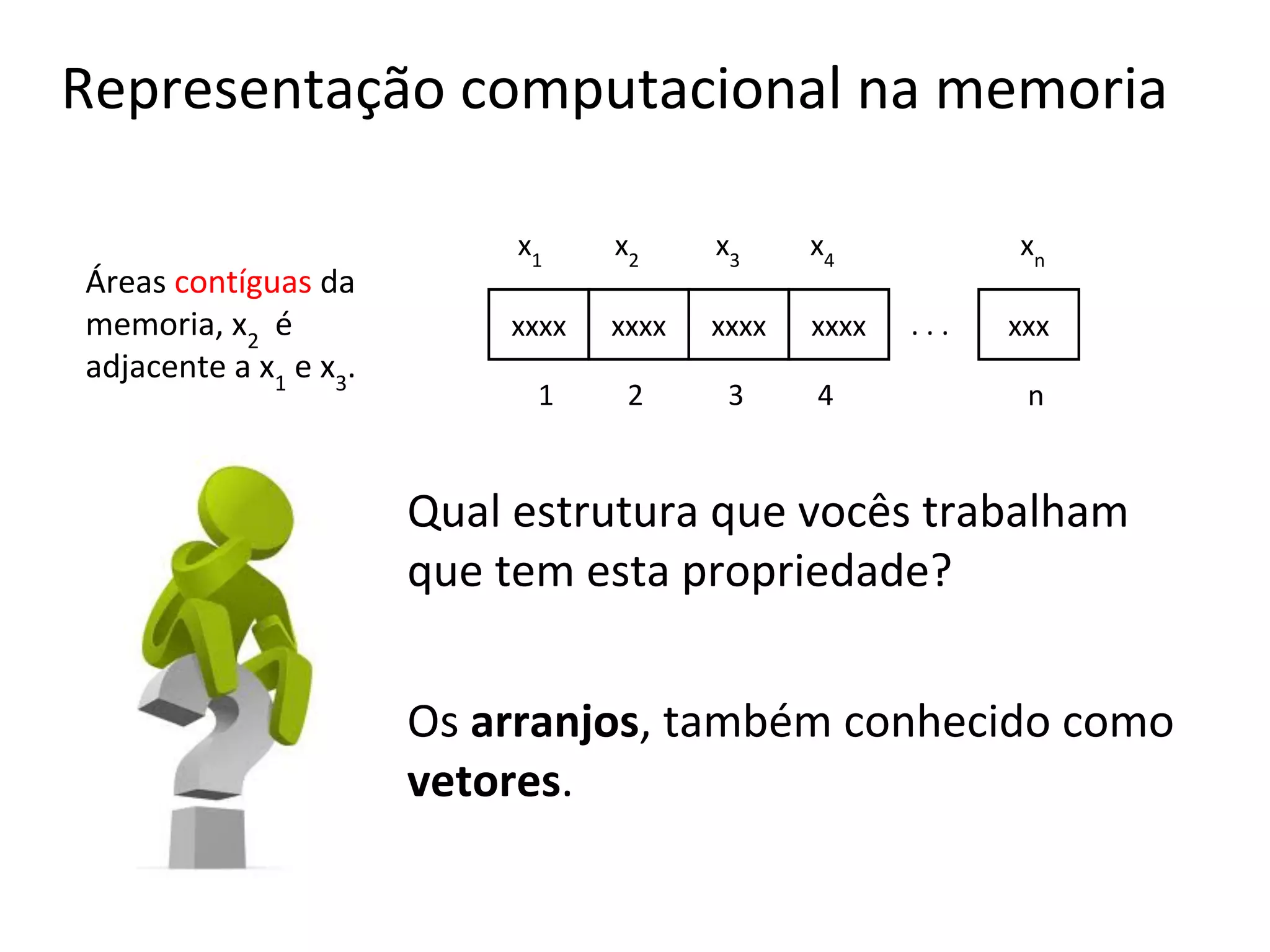
Pode-se implementar uma lista de no máximo MAX elementos, como um
arranjo A[1..MAX]. Este arranjo tem um atributo N[A] que retorna a
quantidade de elementos.
Para MAX=7, temos o seguinte arranjo A:

21. Definição
Pode-se implementar uma lista de no máximo MAX elementos, como um
arranjo A[1..MAX]. Este arranjo tem um atributo N[A] que retorna a
quantidade de elementos.
Para MAX=7, temos o seguinte arranjo A:
Observem que
vamos empregar
a notação similar
ao do clássico
livro (Cormen)

22. Operações: Tamanho
Tamanho ( A)
1.
retorna N[A]
1
A
15
2
6
3
2
4
9
N[A] = 4
5
6
7

23. Operações: Tamanho
Tamanho ( A)
1.
retorna N[A]
1
A
15
2
6
3
2
4
5
6
7
9
N[A] = 4
Como faço para saber se a lista esta
vazia ?

24. Operações: Tamanho
Tamanho ( A)
1.
retorna N[A]
1
A
15
2
6
3
2
4
5
6
7
9
N[A] = 4
Como faço para saber se a lista esta
vazia ?
Se Tamanho (A) = 0 então
faço algo

25. Operações: Inserção
1
Inserir( A, x)
1.
Se N[A] < MAX então
2.
N[A] <- N[A] + 1
3.
A[N[A]] <- x
4.
se não
5.
erro (“lista cheia”);
A
15
2
6
3
2
4
5
6
7
5
6
7
9
N[A] = 4
Inserir ( A, 20)
1
A
15
2
6
3
2
4
9
20
N[A] = 5

26. Problema:
Nas estruturas contíguas é a necessário definir o
seu tamanho a priori, podendo levar a:
●
●
um superdimensionamento (desperdiço de
mémoria) ou
um subdimensionamento (impossibilidade de
inserir mais elementos).

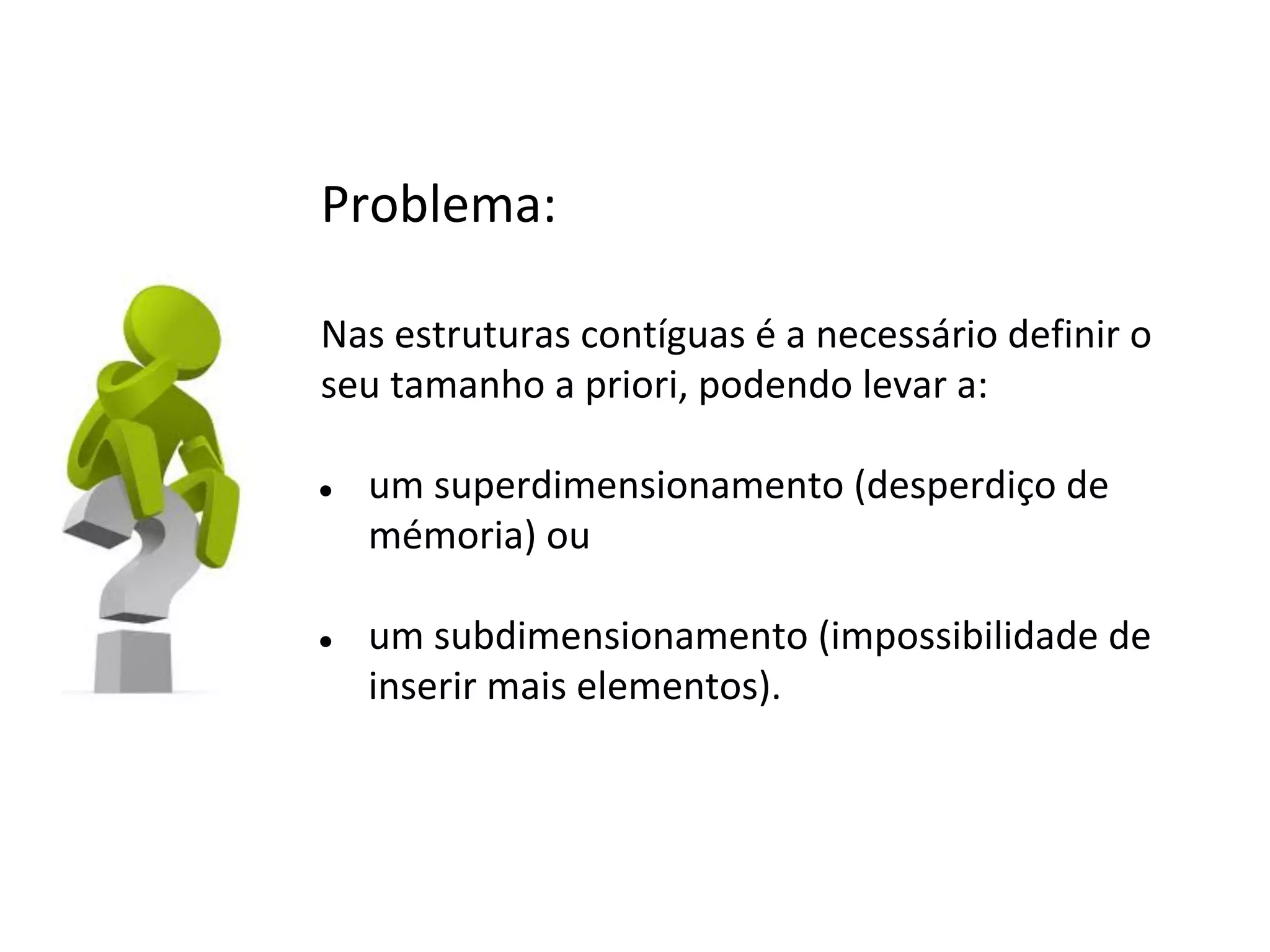
27. Operações: Busca
1
Busca ( A, x)
1.
para i <- 1 ate N[A] faça
2.
se A[i] = x então
3.
retorna i
4.
fim se
5.
fim para
6.
retorna 0
A
15
2
6
3
2
4
9
5
6
7
20
Busca ( A, 2)
1
A
15
2
6
3
2
Explorados
4
9
5
6
7
20
Não explorados

28. Operações: Busca
1
Busca ( A, x)
1.
para i <- 1 ate N[A] faça
2.
se A[i] = x então
3.
retorna i
4.
fim se
5.
fim para
6.
retorna 0
Essa busca é conhecida
como linear ou
sequencial, vocês
aprenderam outras
abordagens.
A
15
2
6
3
2
4
9
5
6
7
20
Busca ( A, 2)
1
A
15
2
6
3
2
Explorados
4
9
5
6
7
20
Não explorados

29. Operações: ElementoEm
Como são áreas contíguas e indexadas, basta
retornar o elemento em A[i].
1
ElementoEm( A, i)
1.
retorna A[i]
A
15
2
6
ElementoEm(A, 4)
3
2
4
9
5
20
9
6
7

30. E a remoção ?

31. E a remoção ?
Lembre que posso querer remover um
elemento em qualquer posição, no inicio,
meio ou fim.

32. E a remoção ?
Lembre que posso querer remover um
elemento em qualquer posição, no inicio,
meio ou fim.
Precisamos manter as propriedades da lista,
xi+1 suceder xi.

33. Operações: Remover
Remove um elemento com um dado índice i.
Movo os elemento de A[i+1..n] para A[i..
n].
1
A
15
2
6
3
2
4
9
5
6
7
20
N[A] = 5
Remover( A, k)
1.
para i <- k até N[A]-1 faça
2.
A[i] = A[i+1]
3.
fim para
4.
N[A] = N[A] - 1
5.
retorna 0
Remover ( A, 3)
1
A
15
2
6
3
9
4
5
20
20
N[A] = 4
6
7

34. Pontos chaves
●
●
●
●
Estrutura de dados lista é uma das mais
importantes e fundamentais.
Conceito chave da lista é a linearidade,
podemos falar em primeiro, segundo ....
Pode ser codificada usando estruturas
contíguas e encadeadas
Estruturas contíguas o tamanho é dado a
priori.